基于模型试验的软夹层地基与刚性地基上隔震结构体系耗能特性分析

于　旭, 庄海洋, 朱　超

(1.南京工程学院 建筑工程学院, 南京　211167; 2.南京工业大学 交通学院, 南京　210009)

基于模型试验的软夹层地基与刚性地基上隔震结构体系耗能特性分析

于旭1,2, 庄海洋2, 朱超2

(1.南京工程学院 建筑工程学院, 南京211167; 2.南京工业大学 交通学院, 南京210009)

摘要：基于能量分析法提出了考虑土-结构动力相互作用(SSI效应)的隔震结构体系能量反应平衡方程，通过对软夹层地基和刚性地基上隔震结构体系振动台模型试验的耗能分析，研究了软夹层地基和刚性地基上隔震结构体系的耗能特性。研究结果表明：提出的土-隔震结构动力相互作用体系能量反应平衡方程能够有效地反映土-隔震结构动力相互作用体系各部分的能量反应。由于SSI效应的影响，软夹层地基上隔震结构隔震层的滞回变形耗能比、动能能量比和阻尼耗能比与刚性地基时耗能反应明显不同，大震时SSI效应影响更为显著，表现为隔震结构的动能能量比和阻尼耗能比增大，而隔震层的滞回变形耗能比降低，降低幅度与输入地震动的特性相关。软夹层地基上隔震结构的动能能量比与隔震层转动效应的强弱密切相关，阻尼耗能比与隔震结构体系的阻尼比相关。

关键词：隔震结构；能量反应方程；土-结构动力相互作用；阻尼比

隔震技术作为一种合理、有效的减震技术已广泛应用于建筑工程领域，隔震结构通过在上部结构和基础之间设置隔震支座和能量耗散装置具有很好的能量耗散能力，减少地震能量向上部结构输入，降低上部结构的地震反应。然而，已有的研究表明：当隔震结构建于软弱地基时由于土与结构动力相互作用(Soil-Structure-Interaction, SSI)的影响，隔震结构体系的自振周期、阻尼等参数将改变，结构地震反应特征将发生变化[1-4]，导致软弱地基上隔震结构的耗能特性与刚性地基假定时并不完全相同。因此，基于软弱地基和刚性地基上隔震结构体系的振动台模型试验，通过能量分析法对比分析两种地基上隔震结构体系的耗能特性，析取软弱地基上SSI效应对隔震结构耗能的影响机理及其规律，对完善软弱地基上隔震结构的抗震设计理论具有十分重要的意义。

Housner[5]首次引入“能量分析”的概念，将能量的平衡关系应用于简单结构的设计中。Bertero等[6]则认为用结构总输入能来比较和判断地面运动对结构物的破坏强度是很有效的。近30年来，从地震能量输入与结构能量耗散间的相互关系来分析研究结构的地震反应和损伤水平的方法日益受到国内外地震工程界的重视。近年来，国内学者相继将地震能量输入与结构能量耗散间的相互关系运用于隔震结构的计算分析中，并取得了一定的成果。杨晓婧等[7]以能量平衡原理为基础，建立基础隔震结构的能量简化设计方法，对隔震结构的力和位移反应进行预测；汪洁等[8]建立了基础隔震结构的地震能量响应方程，研究了铅芯橡胶支座主要参数和不同地震动激励对基础隔震结构非线性地震能量响应的影响；熊仲明等[9]采用能量法对隔震结构体系进行地震反应分析时，找到一种等代体系来简化隔震体系的求解过程。裴星洙等[10]建立地震作用下隔震结构在最大地震响应时刻的能量平衡方程，给出隔震结构隔震层和非隔震层的弹性振动能、塑性能的表达式。但上述基于能量法的隔震结构研究均采用刚性地基假定，不考虑SSI效应的影响。

本文基于非隔震结构考虑SSI效应的力学模型，同时考虑一般土性地基上隔震结构体系的动力反应特征，提出了隔震结构考虑SSI效应的力学模型，并建立了隔震结构考虑SSI效应的能量反应方程。在江苏省自然科学基金的资助下，本文进行了软夹层地基上多层隔震结构体系振动台模型试验，对软夹层地基和已开展的刚性地基上隔震结构模型体系的试验结果进行了系统的耗能反应分析，研究了软夹层地基上SSI效应对隔震结构耗能反应的影响规律。本文的研究成果有助于更好地理解软弱地基隔震结构的隔震机理及其性能，完善软弱地基上隔震结构的抗震设计理论。

1考虑SSI效应时隔震结构的能量反应方程

非隔震结构考虑土-结构动力相互作用(SSI)时，上部结构的惯性力通过基础反馈给地基，将使地基产生局部变形，使基础相对于地基产生平移和转动。Sivanovic[11]通过对地震观测资料的长期研究发现：地震中土-结构相互作用十分明显，主要表现为基础的摆动。鉴于上述现象，吴世明[12]建立了非隔震结构考虑SSI效应时的力学模型和多质点简化分析模型(如图1(a)、(b)所示)。作者已进行的一般土性地基上隔震结构体系振动台模型试验发现：隔震结构基础及隔震层存在转动效应，且隔震层与隔震结构基础的转动反应并不相同，隔震结构的加速度反应表现为隔震层摆动分量与隔震结构弹塑性变形分量的耦合[13-14]。有鉴于此，可建立隔震结构考虑SSI效应的力学模型(如图2(a)所示)，相应的多质点简化分析模型如图2(b)所示。图中hi为上部结构各层质心到隔震层的距离，h0为隔震层高度，ui为上部结构相对于隔震层的水平位移，mi、ki和ci为上部结构各层的质量、刚度及阻尼，m0、k0和c0为隔震层的质量、水平刚度及阻尼，u0为隔震层相对于基础的水平位移，uf、θ1分别为基础重心相对于地基的水平位移和转角，θ为隔震层转角，ug为地面水平位移。

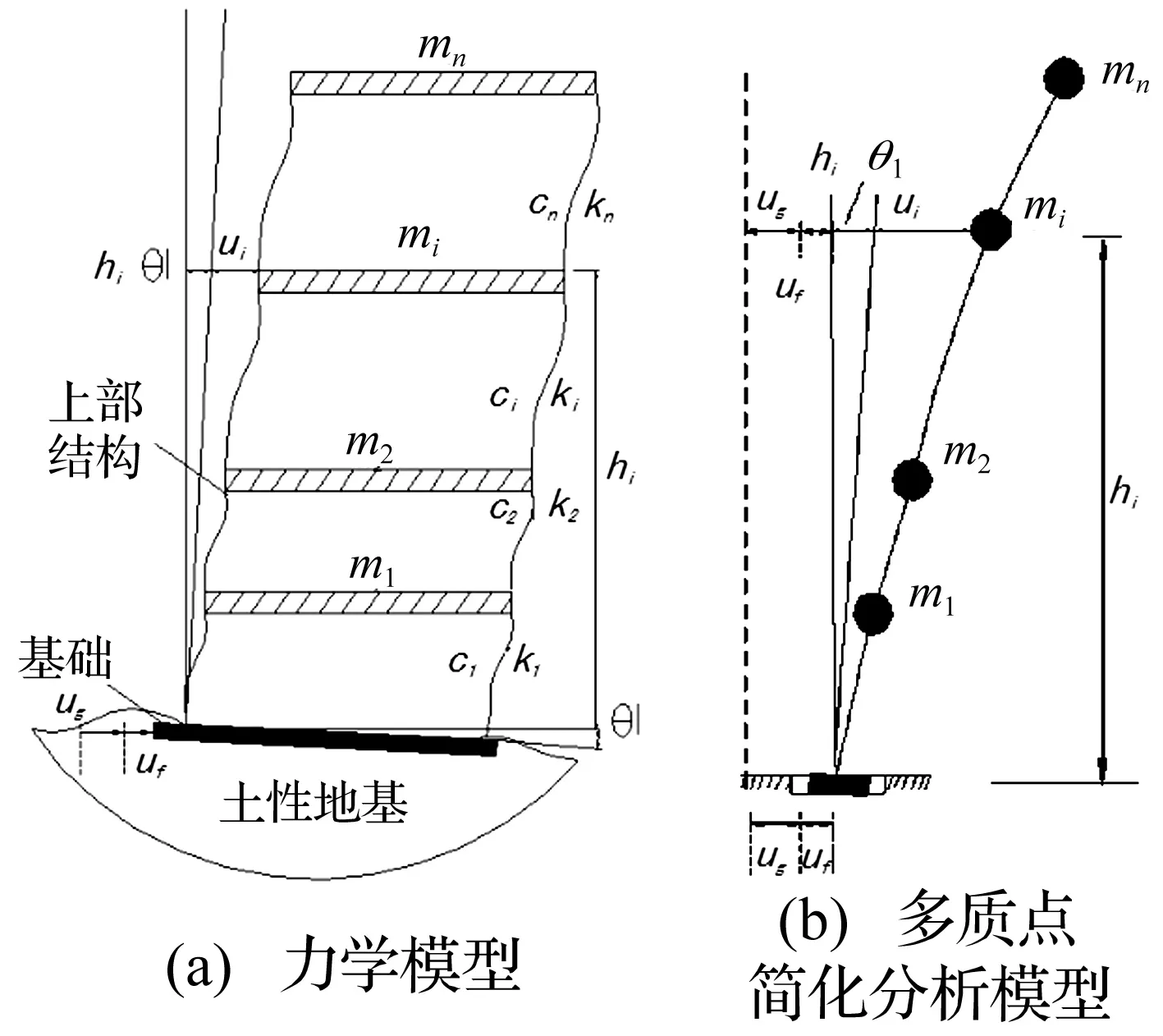
图1　非隔震结构考虑SSI效应的计算模型Fig.1 Calculation model for non-isolated structure with SSI effect

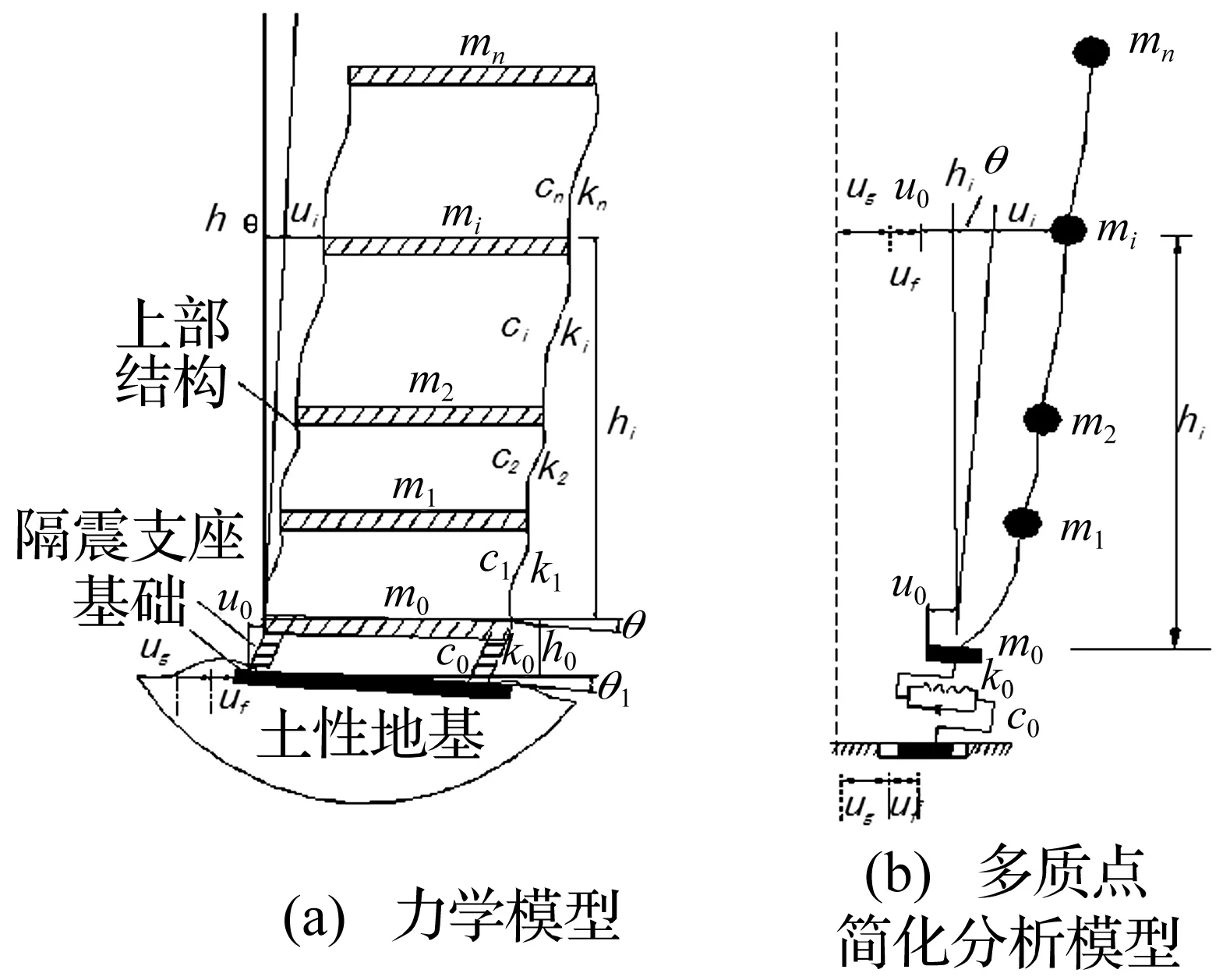
图2　隔震结构考虑SSI效应的计算模型Fig.2 Calculation model for isolated structure with SSI effect

根据图2(b)所示的简化分析模型，可建立隔震结构考虑SSI效应时在水平地震作用下的运动微分方程:

(1)

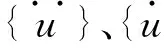
取式(1)两端对各质点相对地面的位移x在地震动持时范围[0，t]内的积分，可得隔震结构体系考虑SSI效应时相对能量反应方程式：

(2)

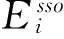
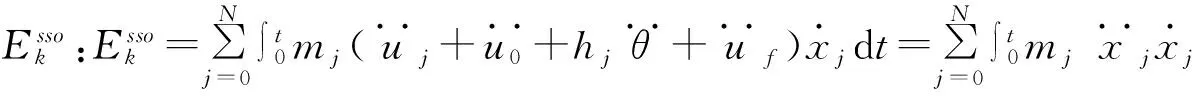
在任意时刻t，考虑SSI效应时隔震结构体系各部分能量应保持平衡，即有:

图4—6分别给出CEBA在基于市场数据下标定3种期权定价模型参数的寻优迭代过程以及由标定参数计算出的期权价格和市场期权价格的对比。对比3条迭代的特征曲线可以发现，标定Merton模型时收敛最快,其次是Heston模型,最慢的是Bates模型,这与解空间维数和模型的复杂度相匹配。从图中也可以清楚地看出市场数据和3种模型模拟(标定)的期权价格的差异都不大,最为吻合的是Bates模型,其次是Heston模型,最差的是Merton模型,这可能源于模型对市场刻画的准确度,即Bates模型对此时的市场刻画最为准确。

(3)

目前，隔震结构设计均采用刚性地基假定，不考虑SSI效应的影响，刚性地基上隔震结构在水平地震作用下的运动微分方程[15]可表示为:

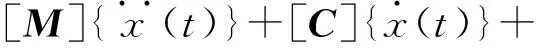
(4)

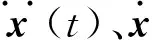
取式(4)两端对质点相对位移x在地震动持时范围[0，t]内的积分，可得刚性地基上隔震结构体系的相对能量反应方程式：

(5)

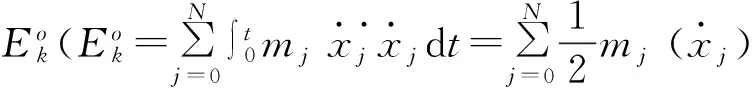
在任意时刻t，刚性地基上隔震结构体系的各部分能量应保持平衡，即有:

(6)

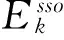
2软夹层地基与刚性地基上隔震结构体系模型试验

2.1试验概况

作者于2009年和2014年分别进行了刚性地基和软夹层地基上多层隔震结构体系振动台模型试验，刚性地基上隔震结构体系振动台模型试验详见文献[16]，软夹层地基上隔震结构体系振动台模型试验选取几何长度、弹性模量和加速度为基本物理量，根据Bukingham定理,导出其他物理量的相似比，试验相似比设计参见文献[17]。软夹层地基和刚性地基上隔震结构模型相同均采用四层钢框架结构[18]，模型底层0.6 m，其余各层0.5 m，激振方向模型高宽比为2.625，每层配重736 kg，总配重3 680 kg,隔震支座采用4个直径为100 mm的铅芯橡胶支座。软夹层地基模型土采用3层分层土，自上而下分别为干砂土、含水量较高的黏土(含水量实测值为27.2%～30.0%)、饱和密实砂土，分层土形成“软夹层地基”，各土层厚度分别为30 cm、40 cm、60 cm。试验加载前采用SDMT波速检测仪测定土层平均剪切波速约为35～40m/s，模型土满足模拟软弱地基的试验要求。模型基础采用2×3群桩基础。试验中模型土箱采用南京工业大学岩土工程研究所研制的层状剪切变形土箱[19]，该土箱可有效减小模型土层人工边界的影响。刚性地基与软夹层地基上隔震结构上部结构传感器相同，软夹层地基上试验模型传感器布置见图3，图中A1～A17为水平加速度计，V1～V4为竖向加速度计，S1～S5为位移计，t1～t3为土压力计，E1～E8为应变片。试验采用单向激振， 选用地震波为 El Centro波、Kobe波、南京人工波3条地震波，软夹层地基上试验加载方案如表1所示，刚性地基上模型试验的加载方案见文献[16]。软夹层地基上模型体系试验图片如图4所示。

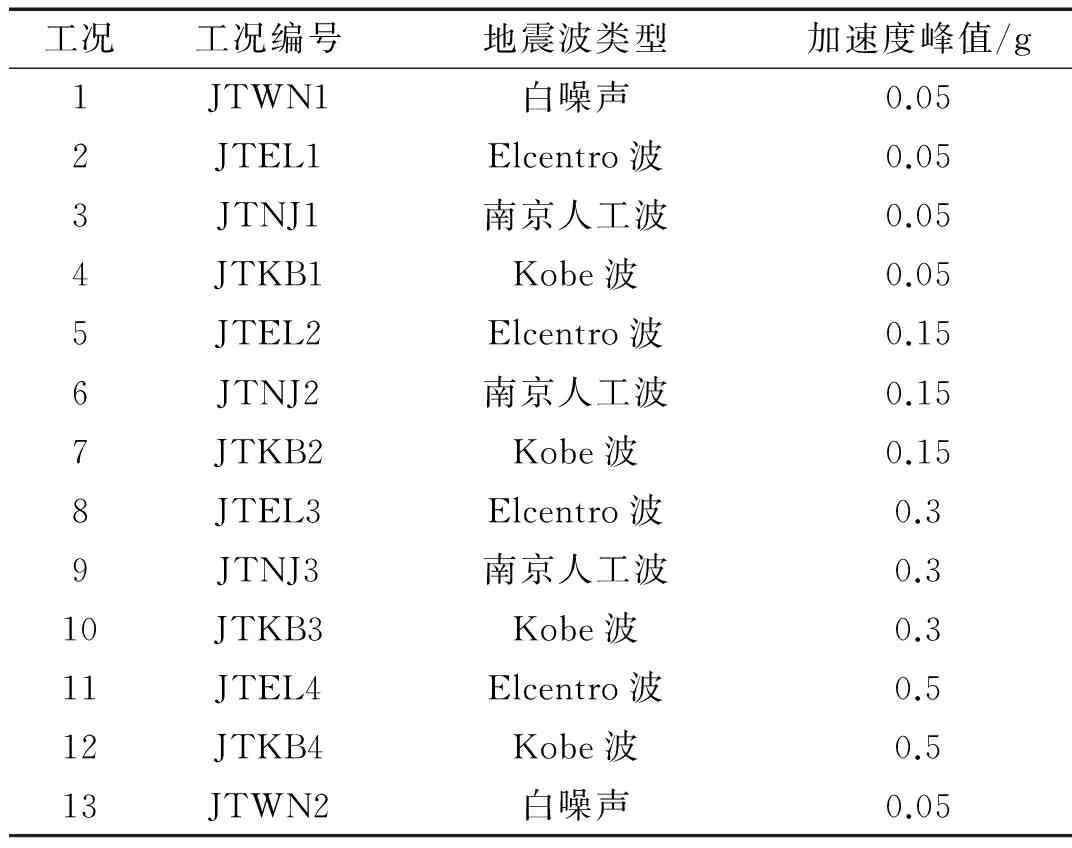
表1　试验加载工况

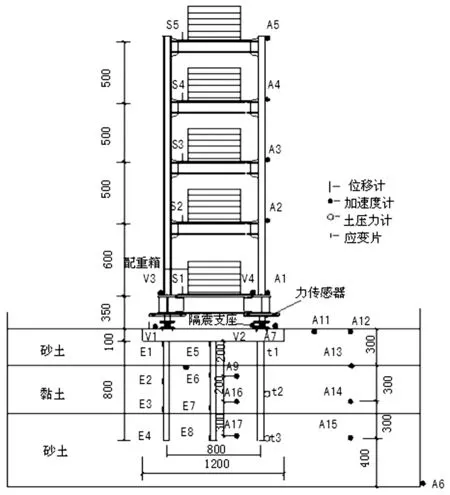
图3　模型体系布置及测点布置图Fig.3 Sketch of model system arrangement and measuring point arrangement

图4　模型试验图片Fig.4 Photo of test model

2.2试验结果

软夹层地基上隔震结构一阶自振频率f1=2.4 Hz，阻尼比ξ1=0.148。由文献[10]可知，刚性地基上隔震结构一阶自振频率f1=2.65 Hz，阻尼比ξ1=0.083。

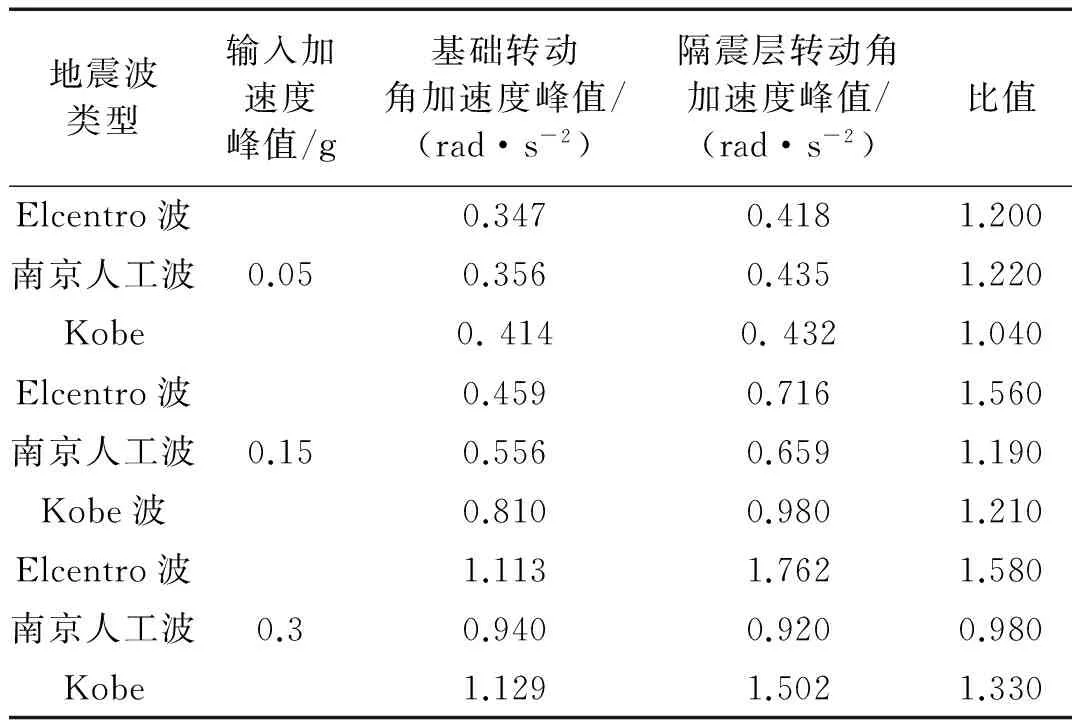
表2　 软夹层地基上基础及隔震层转动角加速度峰值

图6为软夹层地基与刚性地基上典型的隔震结构铅芯橡胶支座滞回特性曲线(输入地震动加速度峰值为0.3 g )。由图6可知，相同的地震动输入下，软夹层地基与刚性地基上铅芯橡胶支座滞回环面积并不相同，表现为：软夹层地基上铅芯橡胶支座滞回环面积较刚性地基时呈不同幅度的降低，降低幅度与输入地震动的特性有关。

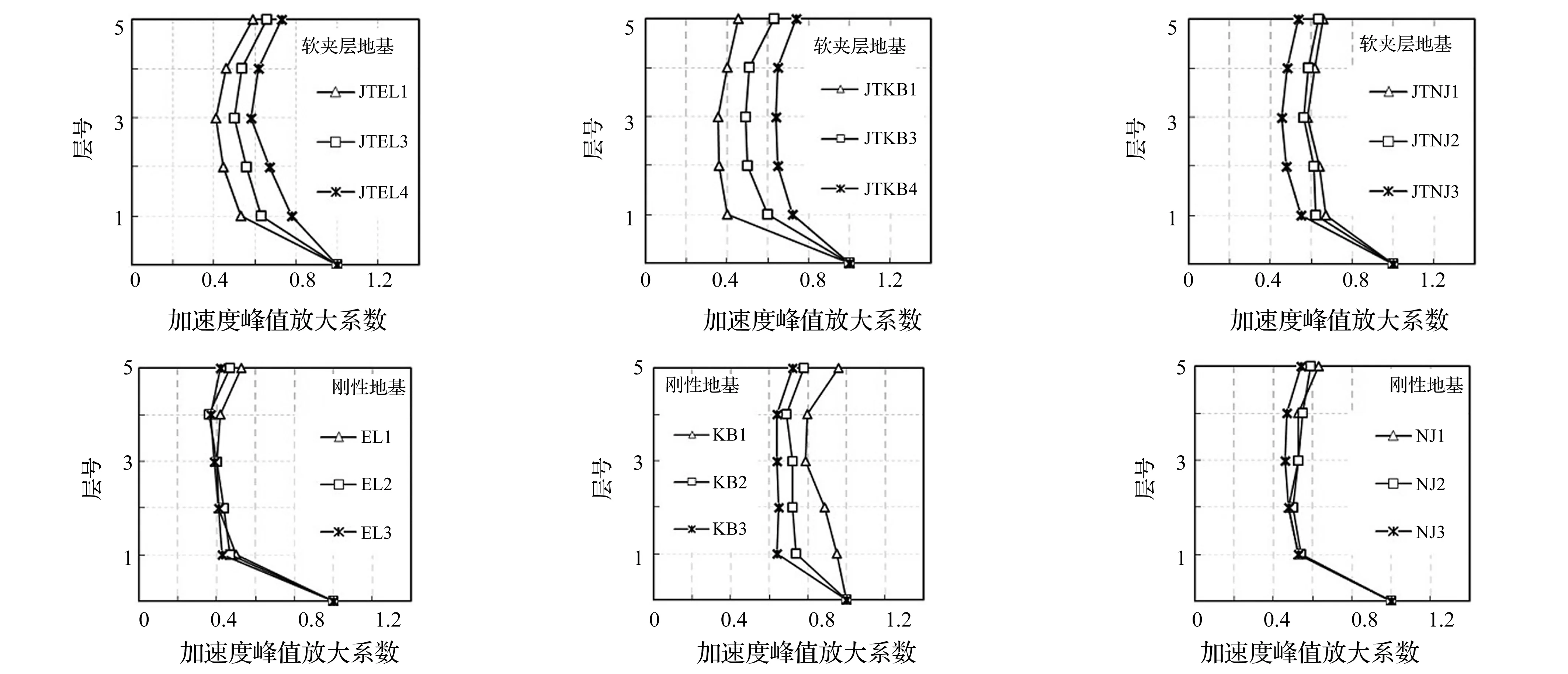
(a) Elcentro波(b) Kobe波(c) 南京人工波图5 软夹层地基与刚性地基上隔震结构楼层加速度放大系数Fig.5Accelerationmagnificationfactorofseismicisolatedonsofterinterlayersoilfoundationandrigidfoundation

(a) Elcentro波(b) Kobe波(c) 南京人工波图6 软夹地基与刚性地基上隔震结构隔震支座滞回曲线Fig.6Hysteresisofisolatoronsofterinterlayersoilfoundationandrigidfoundation

3软夹层地基与刚性地基上隔震结构体系耗能特性分析

3.1模型耗能计算参数

刚性地基与软夹层地基上模型隔震层参数和上部结构物理参数相同，分别如表3和表4所示。

表3　模型体系隔震层参数

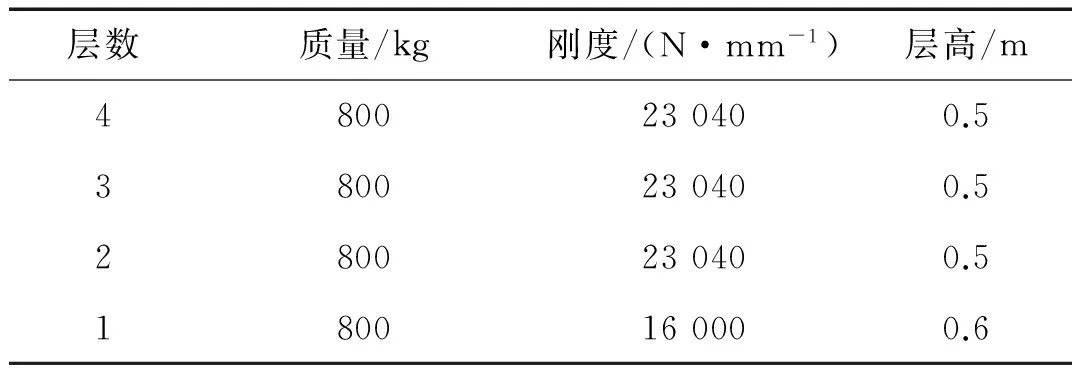
表4　模型体系上部结构各层质量及刚度

试验中测得刚性地基上隔震结构一阶自振频率f1=2.65 Hz，阻尼比ξ1=0.083，软夹层地基上隔震结构一阶自振频率f1=2.4 Hz，阻尼比ξ1=0.148。模型体系阻尼系数采用瑞雷阻尼系数，阻尼矩阵表达式为：

[C]=α[M]+β[K]

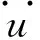
3.2刚性地基上隔震结构体系的耗能分析

根据刚性地基上隔震结构模型体系的地震反应，对模型体系进行能量分析，不同地震动作用下模型体系的总输入能量、各部分能量如表5～表7所示，表中地面加速度峰值Xg为振动台台面实测加速度反应峰值，相应的不同地震动作用下模型体系的各部分能量与总输入能量的比值如图7(a)～图7(c)所示，图中Rk、Rh、Rc和Rd分别为动能能量比、结构滞回变形耗能比、阻尼耗能比和隔震层滞回变形耗能比。输入模型体系的总能量中转化为动能和弹性应变能的部分随时间在零线附近相互转换，该部分能量并未耗散，模型体系的耗能主要通过阻尼耗能和滞回耗能的形式耗散掉。由表5～表7及图7可知，刚性地基上隔震结构体系的耗能具有以下规律：

1) 刚性地基上隔震结构的地震动总输入能量主要由隔震结构隔震层的滞回变形耗能Ed所吸收，大震时隔震结构隔震层的滞回变形耗能比均达到0.8以上，隔震结构的动能能量比Rk和阻尼耗能比Rc较小，而隔震结构上部结构的滞回变形耗能比Rh最小，基本上可以忽略不计；

2) 刚性地基上隔震结构隔震层的滞回变形耗能比Rd与输入地震动的峰值有关。主要表现为输入地震动峰值越大，隔震层滞回变形耗能比Rd越高，表明隔震效果越好。

3) 不同的地震动作用下隔震层的滞回变形耗能比Rd并不相同，El-centro波激振时隔震层滞回变形耗能比最高，地震动总输入能量的83%以上由隔震层的滞回变形耗能所吸收；南京人工波激振时隔震层滞回变形耗能比较Elcentro波激振时略有降低；Kobe波激振在大震时隔震层滞回变形耗能比较高，隔震效果较好，而在小震时隔震层滞回变形耗能比降低，动能能量比增大。

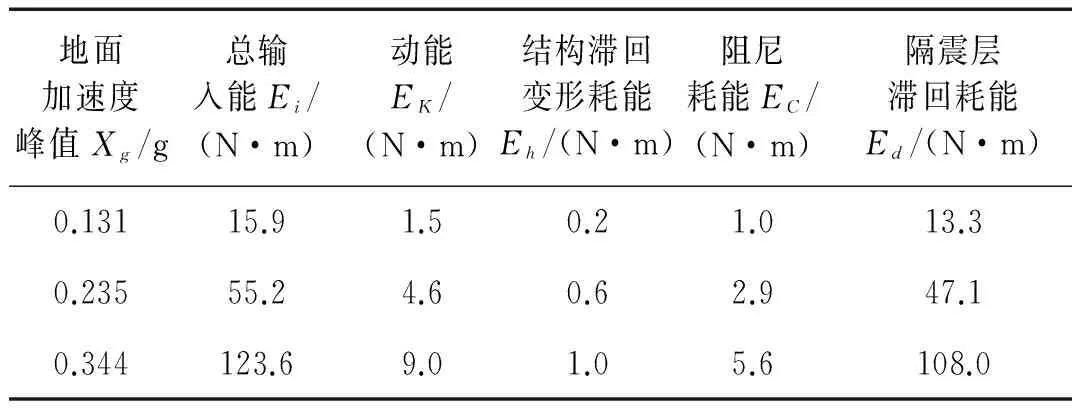
表5　刚性地基上Elcentro波输入时隔震结构的各部分耗能

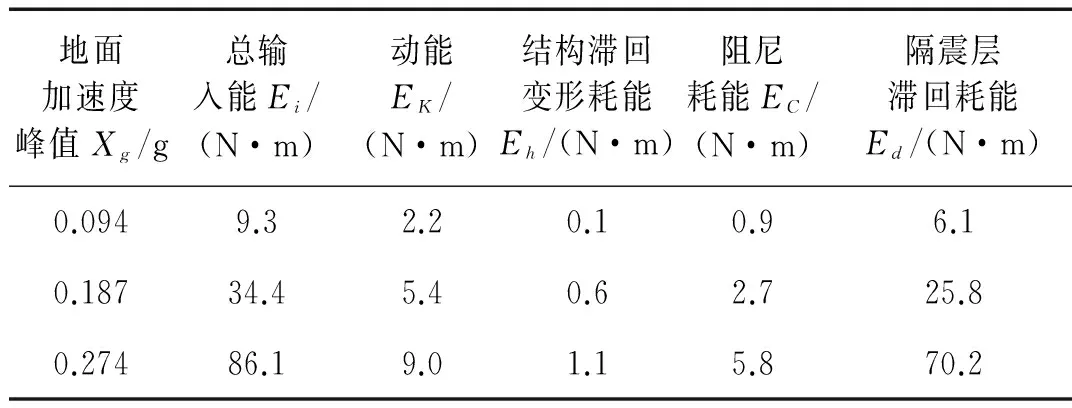
表6　刚性地基上Kobe波输入时隔震结构的各部分耗能

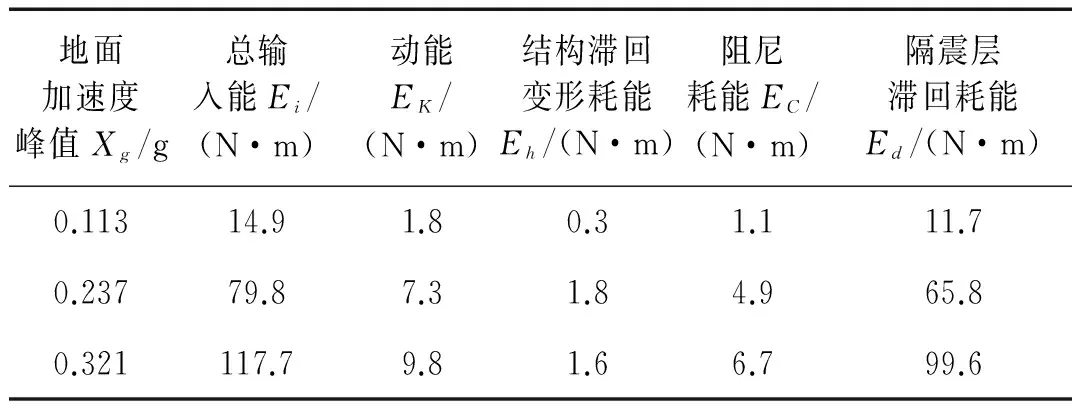
表7　刚性地基上南京人工波输入时隔震结构的各部分耗能

3.3软夹层地基上隔震结构体系的耗能分析

根据软夹层地基上隔震结构模型体系的地震反应模型试验结果，对软夹层地基-隔震结构模型体系进行能量分析，不同地震动作用下模型体系的总输入能量、各部分能量如表8～表10所示，表中地面加速度峰值Ug为土表A12测点的实测加速度反应峰值，相应的不同地震动作用下模型体系的各部分能量与总输入能量的比值如图8(a)～图8(c)所示，图中Rk、Rh、Rc和Rd的含义同本文4.2节。与刚性地基时类似，输入模型体系的总能量中转化为动能和弹性应变能的部分随时间在零线附近相互转换，模型体系的耗能主要通过阻尼耗能和滞回耗能的形式耗散掉，由表8～表10及图8可以看出，软夹层地基上隔震结构体系能量耗散分配与刚性地基时并不相同，隔震结构隔震层的滞回变形耗能比Rd仍占较大比重，但隔震结构的动能能量比Rk和阻尼耗能比Rc发生较大变化，隔震结构上部结构的滞回变形耗能比Rh仍很小，具体来看，软夹层地基上隔震结构体系各部分的耗能具有以下规律：

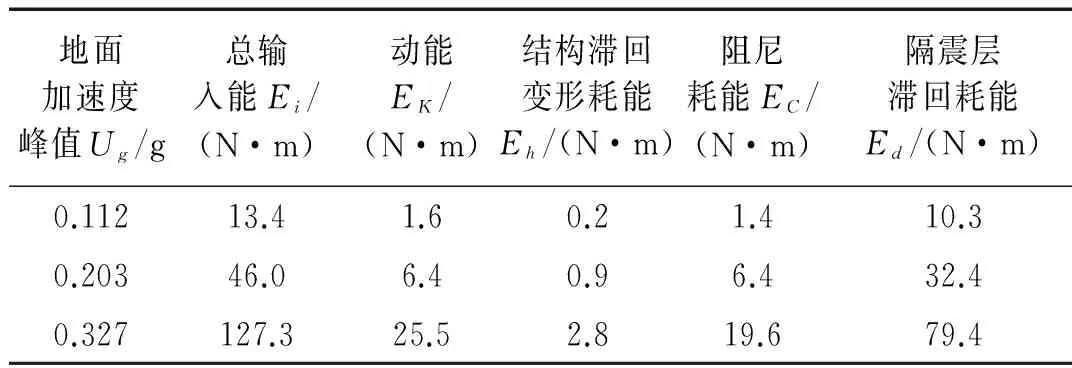
表8　软夹层地基上Elcentro波输入时隔震结构的各部分耗能

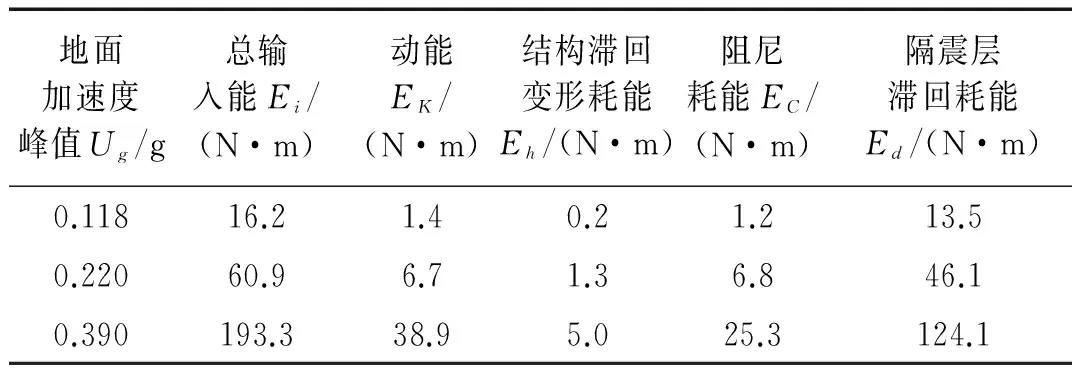
表9　软夹层地基上Kobe波输入时隔震结构的各部分耗能

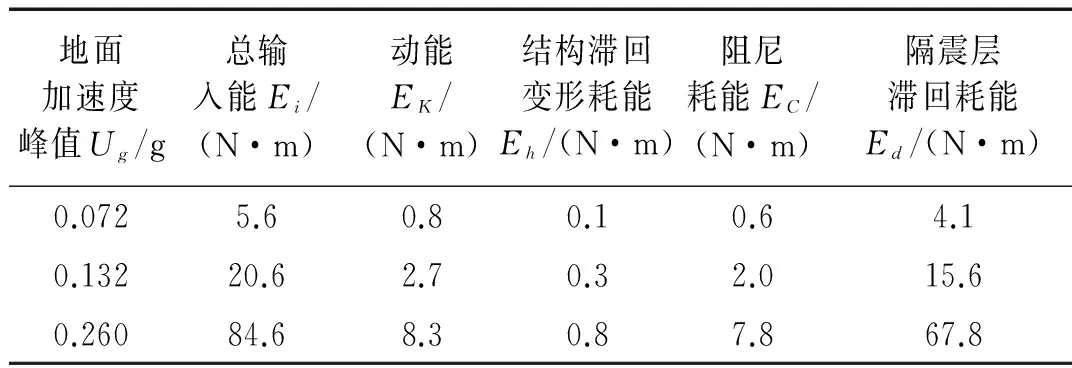
表10　软夹层地基上南京人工波输入时隔震结构的各部分耗能

(a) Elcentro波(b) Kobe波(c) 南京人工波图7 刚性地基上隔震结构各部分耗能比组成Fig.7Ratioofenergydissipationofpartsofisolatedstructureonrigidfoundation

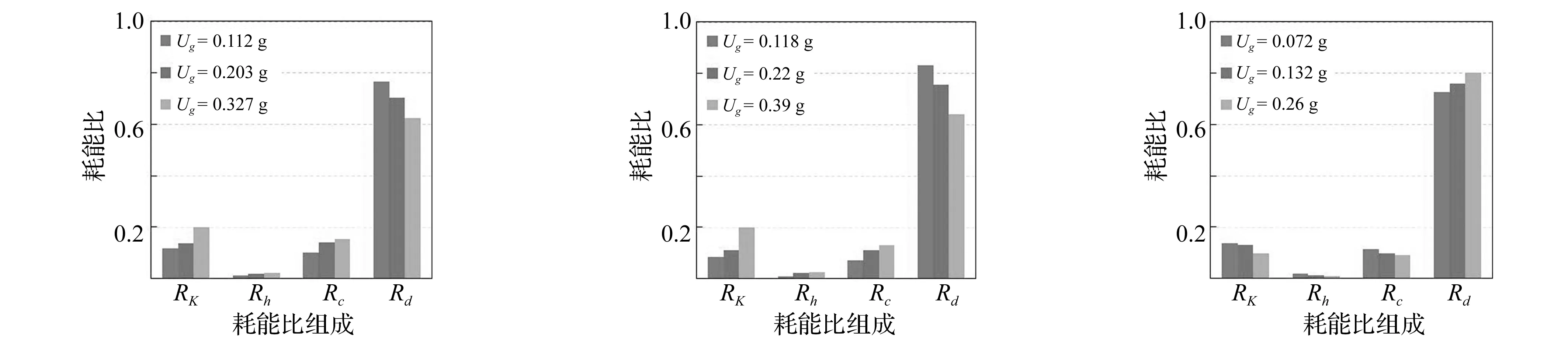
(a) Elcentro波(b) Kobe波(c) 南京人工波图8 软夹层地基上隔震结构各部分耗能比组成Fig.8Ratioofenergydissipationofpartsofisolatedstructureonsofterinterlayersoilfoundation

1) 软夹层地基上隔震结构模型体系动能能量比Rk的变化规律与刚性地基时明显不同，与隔震层转动效应的强弱密切相关。由图7可知，不同地震动小震时刚性地基上隔震结构体系的动能能量比Rk为0.092～0.235，而大震时刚性地基上隔震结构体系的动能能量比Rk为0.073～0.095，表明：刚性地基上隔震结构的动能能量比Rk随输入地震动峰值的增大而降低；由图8可知， Elcentro波和Kobe波小震时软夹层地基上隔震结构动能能量比Rk为0.073～0.102，而大震时动能能量比Rk为0.131～0.154，表明：软夹层地基上Elcentro波和Kobe波激振时隔震结构体系的动能能量比Rk随输入地震动峰值的增大而增大；南京人工波小震时软夹层地基上隔震结构动能能量比Rk为0.114，而大震时动能能量比Rk为0.092，表明：南京人工波激振时动能能量比Rk随输入地震动峰值的增大而减小。上述现象与表2试验结果相吻合的是： Elcentro波和Kobe波激振时隔震层与基础转动角加速度峰值的比值随输入地震动峰值的增大而增大，而南京人工波激振时隔震层与基础转动角加速度峰值的比值随输入地震动峰值的增大而减小。上述分析表明：软夹层地基上隔震结构模型体系动能能量比Rk与隔震层转动效应的强弱相关，当隔震层转动效应增强时，模型体系的动能能量比Rk增大，而隔震层转动效应减弱时，模型体系的动能能量比Rk降低。

(2)软夹层地基上隔震结构阻尼耗能比Rc与刚性地基时并不相同，与隔震结构体系的阻尼比相关。对比图7和图8中隔震体系的阻尼耗能比Rc可以看出，不同地震动作用下刚性地基上隔震结构阻尼耗能比Rc为0.045～0.076，而软夹层地基上隔震结构阻尼耗能比Rc为0.073～0.154，表明：软夹层地基上隔震结构的阻尼耗能比较刚性地基时明显增大，其主要原因是：由于SSI效应的影响软夹层地基上隔震结构体系的阻尼比较刚性地基时大幅增加，相应的隔震结构体系的阻尼耗能比增大。

3) 软夹层地基上隔震结构的地震动总输入能量仍主要由隔震层的滞回变形耗能Ed所吸收，但对比图7和图8可以看出，不同地震动大震时软夹层地基上隔震层的滞回变形耗能比Rd为0.624～0.801，而大震时刚性地基上隔震层的滞回变形耗能比Rd为0.835～0.874，上述分析表明：大震时软夹层地基上隔震层的滞回变形耗能比Rd较刚性地基时降低。其原因主要有以下两方面：① 与刚性地基时隔震结构体系的能量反应方程相比，软夹层地基上隔震结构体系的能量反应方程明显不同，其动能组成中增加了基础平动及隔震层转动的分量，本文3.2节试验结果表明:软夹层地基上隔震结构隔震层有明显的转动角加速度反应(如表2所示)，而前文的分析表明：软夹层地基上隔震结构体系的动能能量比Rk与隔震层转动效应的强弱密切相关；② 由于SSI效应的影响，软夹层地基上隔震结构体系的动力特性发生较大变化，试验中测得刚性地基上隔震结构的阻尼比为0.083，而软夹层地基上隔震结构的阻尼比为0.148，阻尼比较刚性地基时显著增大，导致相应的软夹层地基上隔震结构体系的阻尼耗能较刚性地基时增加，这将间接降低隔震层的滞回变形耗能比例。由图7和图8的对比可知，大震时上述两方面的影响尤为明显，其中软夹层地基上隔震结构阻尼耗能比Rc较刚性地基时明显增大，而动能能量比Rk在南京人工波输入时较刚性地基时略有增加，在Elcentro波和Kobe波输入时较刚性地基时显著增大。因此，在一定的地震动总输入能下，大震时隔震结构隔震层的滞回变形耗能比较刚性地基时降低。

4) 软夹层地基上隔震结构耗能特性与输入地震动的特性和峰值有关。对比图7和图8中隔震层的滞回变形耗能比可以看出，软夹层地基上El-centro波和Kobe波激振时隔震层的滞回变形耗能比Rd随输入地震动峰值的增大而降低，相应的阻尼耗能比Rc和动能能量比Rk增大，即输入地震动峰值越大，隔震层的耗能越差，这与刚性地基时Rd的规律完全相反；而软夹层地基上南京人工波激振时隔震层的滞回变形耗能比Rd随输入地震动峰值的增大而增大，相应的阻尼耗能比Rc和动能能量比Rk减小，这与刚性地基时隔震层的滞回变形耗能比Rd的规律相似。

上述现象可做如下解释：隔震结构的机理是采用在建筑的基础和上部结构之间设置柔性隔震层，延长上部结构的基本周期，从而避开地面地震动的主频带范围，减免共振效应，阻断地震能量向上部结构的传递，减小结构的地震反应。对于软弱地基上的隔震结构，场地地震动频谱特性低频化同时，隔震结构的自振频率受SSI效应的影响而改变，可能不利于避开地震动的主频范围，共振效应将对隔震结构的耗能产生影响。在软夹层地基上隔震结构模型试验中，振动台台面A6测点测得的三种输入地震波的傅氏谱如图9所示(台面输入加速度峰值为0.05 g),可以看出， Kobe波的傅氏谱以低频分量为主， Elcentro波的傅氏谱以中低分量为主，而南京人工波傅氏谱频宽最宽，傅氏谱以中高频分量为主。经软夹层地基土层滤波后，土层表面测点A12的频谱组成中低频分量明显增强，其地震动傅氏谱如图10所示，可以看出， El-centro波输入时土表测点A12的主频范围为3.2～7.4 Hz，Kobe波输入时土表测点A12的主频范围为2.8 Hz～6.2 Hz，而南京人工波输入时土表测点A12的主频范围为12.3～15.0 Hz和17.6～22.3 Hz，试验中测得软夹层地基上隔震结构的一阶自振频率为2.4 Hz,其较接近Kobe波和El-centro波的主频范围，而离南京人工波的主频范围相对较远，而软夹层地基上隔震结构的试验结果表明:随着输入地震动加速度峰值的增大，土表测点A12的频谱组成向低频转变的现象越明显，这意味着输入Kobe波和El-centro波时，随输入地震动加速度峰值的增大，隔震结构的一阶自振频率将不断接近地震动的主频范围，共振效应的影响将不断增强，隔震结构的地震反应不断增大，相应的隔震结构的动能和阻尼能不断增大，在总能量一定的情况下，隔震层的滞回变形耗能减小，而输入南京人工波时，隔震结构的一阶自振频率有效避开了地震动的主频范围，减免共振效应，隔震结构的地震反应降低，相应的隔震结构的动能和阻尼能不断减小，在总能量一定的情况下，隔震层的滞回变形耗能增大。因此，上述输入地震动的频谱特性对隔震结构耗能特性的影响表现为：输入地震动的的频谱特性以中低频分量为主时，SSI效应对隔震结构的耗能影响较大，隔震层的滞回变形耗能比不断降低，阻尼耗能比和动能能量比不断增大，隔震效果明显降低；而输入地震动的频谱特性以中高频分量为主时(如南京人工波)，SSI效应对隔震结构的耗能影响较小，隔震结构隔震层的滞回变形耗能比不断增大，阻尼耗能比和动能能量比降低。

(a) ElCentro波(b) Kobe波(c) 南京人工波图9 软夹层场地隔震结构试验中振动台台面A6测点的傅氏谱Fig.9FourierspectraoftestpointA6withsofterinterlayerfoundation

(a) ElCentro波(b) Kobe波(c) 南京人工波图10 软夹层场地隔震结构试验中土表A12测点的傅氏谱Fig.10FourierspectraoftestpointA12withsofterinterlayerfoundation

4结论

本文基于能量分析法建立了考虑SSI效应的隔震结构体系能量反应平衡方程，通过对软夹层地基和刚性地基上隔震结构体系振动台模型试验结果的耗能反应分析，研究了刚性地基和软夹层地基上隔震结构体系的耗能特征及其规律，得到的主要结论有：

(1) 提出了考虑SSI效应的隔震结构体系能量反应平衡方程，该方程概念明确，经对模型试验体系的能量反应分析，证明其能有效地反映土-隔震结构动力相互作用体系各部分的能量分配规律；

(2) 刚性地基上隔震结构的耗能主要由隔震层的滞回变形耗能为主，随着输入地震动增强，隔震层滞回耗能比也不断变大，即说明地震越强，隔震效果越好。大震时隔震层的滞回变形耗能比达到0.8以上，而上部结构滞回变形耗能最小，基本上可以忽略不计；

(3) 软夹层地基上隔震结构的耗能虽然仍以隔震层的滞回变形耗能为主，但大震时软夹层地基上隔震层的滞回变形耗能较刚性地基时降低。说明软夹层地基上隔震层的隔震效率降低。

(4) 软夹层地基上SSI效应对隔震结构耗能的影响与输入地震动的特性和峰值有关。在以中低频分量为主的地震动作用下，SSI效应对隔震层的耗能影响较大，隔震层的滞回变形耗能比不断降低，隔震结构阻尼耗能比和动能能量比不断增大，隔震层的隔震效果明显降低；而输入地震动的频谱特性以中高频分量为主时，SSI效应对隔震体系的耗能影响较小，隔震层的滞回变形耗能比不断增大，阻尼耗能比和动能能量比降低。

参 考 文 献

[1] 日本建筑学会著.隔震结构设计[M].刘文光,译. 北京: 地震出版社, 2006:110-140.

[2] Dezi F, Carbonari S, Tombari A, et al. Soil-structure interaction in the seismic response of an isolated three span motorway over crossing founded on piles[J]. Soil Dynamics and Earthquake Engineering, 2012, 41: 151-163.

[3] Takaji K. Seismic base-isolation mechanism in liquefied sand in terms of energy[J]. Soil Dynamics and Earthquake Engineering, 2014, 63: 92-97.

[4] Enrique Luco J. Effects of soil-structure interaction on seismic base isolation[J]. Soil Dynamics and Earthquake Engineering, 2014, 66: 167-177.

[5] Housner G W.Limit design of strutures to resist earthquake [C]//Proc of IWCEE. Berkeley, CA, 1956.

[6] Bertero V V，Uang C M.Evaluation of seismic energy in structures[J]. Earthquake Engrg, and Struct,Dynamics, 1990,19(1):77-90.

[7] 杨晓婧,王曙光，杜东升，等. 基础隔震结构基于能量法的反应预测[J]. 工程抗震与加固改造,2010, 32(1):34-37.

YANG Xiao-jing, WANG Shu-guang, DU Dong-sheng, et al, Response analysis for base-isolated structure based on energy theory [J]. Earthquake Resistant Engineering and Retrofitting,2010, 32(1):34-37.

[8] 汪洁,李宇. 三维基础隔震结构非线性地震能量响应分析[J]. 西安建筑科技大学学报:自然科学版, 2013, 45(3):367-370.

WANG Jie, LI Yu. Response analysis for base-isolated structure based on energy theory[J]. J Xi’an Univ of Arch & Tech:Natural Science Edition, 2013, 45(3):367-370.

[9] 熊仲明, 张萍萍,韦俊，等. 滑移隔震结构基于能量分析的简化计算方法研究[J]. 西安建筑科技大学学报:自然科学版, 2012, 44(3):305-310.

XIONG Zhong-ming, ZHANG Ping-ping,WEI Jun, et al. Study on the simplified method of energy analysis based on sliding isolation structure [J]. J Xi’an Univ of Arch & Tech:Natural Science Edition, 2012, 44(3):305-310.

[10] 裴星洙, 王维, 王星星. 基于能量原理的隔震结构地震响应预测法研究[J]. 工程力学, 2011, 28(7):65-72.

PEI Xing-zhu, WANG Wei, WANG Xing-xing. Earthquake response prediction of isolated structures based on energy principle[J]. Engineering Mechanics,2011, 28(7):65-72.

[11] Sivanovic S. Seismic response of an instrumented reinforced concrete building founded on piles[C]//Proc of 12WCEE. Auckland, New Zealand, 2000.

[12] 吴世明. 土动力学[M]. 北京: 中国建筑工业出版社, 2000:284-291.

[13] 于旭,宰金珉,王志华.考虑SSI效应的铅芯橡胶支座隔震结构体系振动台模型试验[J].南京航空航天大学学报, 2010, 42(6): 786-792.

YU Xu, ZAI Jin-min, WANG Zhi-hua. Shaking table model test on lead core rubber bearing in isolation structure system considering SSI [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(6): 786-792.

[14] Zhuang Hai-yang, Yu Xu, Zhu Chao, et al. Shaking table tests for the seismic response of a base-isolated structure with the SSI effect [J]. Soil Dynamics and Earthquake Engineering, 2014, 67(6): 208-218.

[15] 周云, 徐彤, 周福霖. 抗震与减震结构的能量分析方法研究与应用[J].地震工程与工程振动,1999, 19(4):133-139.

ZHOU Yun, XU Tong, ZHOU Fu-lin. Research and development of structural seismic design based on energy method[J].Earthquake Engineering and Engineering Vibration,1999, 19(4):133-139.

[16] 于旭,宰金珉,王志华.铅芯橡胶支座隔震钢框架结构体系振动台模型试验研究[J].世界地震工程，2010，26(3)：30-36.

YU Xu, ZAI Jin-min, WANG Zhi-hua. Shaking table tests on the model of a steel-framed structure system with lead core rubber bearing isolations[J].World Earthquake Engineering, 2010，26(3)：30-36.

[17] 于旭. 考虑土与结构相互作用的隔震结构体系性能研究[D]. 南京:南京工业大学, 2009.

[18] Yu Xu, Zai jin-ming，Liu wei-qing. Experimental research and nonlinear finite element analysis on novel joint between CFRT column and steel beam[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2009，26(1)：75-82.

[19] 陈国兴,王志华,左熹.振动台试验叠层剪切型土箱的研制[J]. 岩土工程学报, 2010,32(1):89-97.

CHEN Guo-xing, WANG Zhi-hua, ZUO Xi. Development of laminar shear soil containner for shaking table tests [J].Chinese Journal of Geotechnical Engineering，2010,32(1):89-97.

Analysis on the energy dissipation of isolated structures on rigid foundation and soft interlayer soil foundation based on model test

YU Xu1,2, ZHUANG Hai-yang2, ZHU Chao2

(1. Department of Civil Engineering, Nanjing Institute of Technology, Nanjing 211167, China;2. Institute of Geotechnical Engineering, Nanjing Tech University, Nanjing 210009, China)

Abstract:Based on the energy method, energy response equations for a soil-isolated structure interaction system were established. By comparative analysis on the energy dissipation of isolated structures set on different foundations in shaking table tests, the characteristics of energy dissipation of isolated structures set on soft interlayer soil foundation and rigid foundation were studied. The results show that the energy response equations proposed can illustrate the pattern of energy distribution of the soil-isolated structure interaction system. The enegy of ground motion input to the isolated structure on soft interlayer soil foundation is dissipated mainly by the hysteresis deformation of isolation layer. On soft interlayer soil foundation, the hysteresis deformation energy ratio of isolation layer, the kinetic energy ratio and damping energy ratio of isolated structure are different from those on rigid foundation. The peak acceleration of input motion is larger and the soil-structure interaction (SSI) effect has a significant influence on the energy dissipation of isolated structure, that is, the kinetic energy ratio and damping energy ratio of isolated structure increase and the energy dissipation of isolation layer decrease, which is related to the characteristics of input earthquake motion. In the case of soft interlayer soil foundation, the ratio of kinetic energy is related to the rotation effect of isolation layer, and the ratio of damping energy is related to the damping ratio of isolated structure.

Key words:isolated structure; energy response equation; soil-structure interaction; damping ratio

基金项目：江苏省自然科学基金青年基金资助项目(BK2012477);南京工程学院校级科研基金项目(CKJA201505)

收稿日期：2015-03-19修改稿收到日期：2015-05-31

通信作者庄海洋 男，博士，教授，1978年2月生

中图分类号:TU311

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.012

第一作者 于旭 男，博士，副教授，1977年3月生

E-mail: zhuang7802@163.com