一种船舶舷侧外板骨材抗撞性能解析预报模型

孙　斌， 胡志强， 王　晋,2

(1. 上海交通大学 海洋工程国家重点实验室，上海　200240；2.高泰深海技术有限公司, 休斯敦　77079)

一种船舶舷侧外板骨材抗撞性能解析预报模型

孙斌1， 胡志强1， 王晋1,2

(1. 上海交通大学 海洋工程国家重点实验室，上海200240；2.高泰深海技术有限公司, 休斯敦77079)

摘要：以典型的船舶舷侧外板上的骨材为研究对象，运用塑性力学理论及数值仿真技术，分析了舷侧外板上骨材在遭受带有球鼻艏的船舶撞击场景下的变形损伤机理。研究中应用LS_DYNA仿真模拟得到舷侧外板上骨材的变形模态和能量耗散结果，在此基础上建立起骨材塑性变形的几何数学模型。运用塑性力学理论，获得舷侧外板上骨材在变形过程中的能量损耗和平均变形阻力的解析计算公式。研究中应用数值仿真结果进行验证。研究得到的舷侧外板骨材变形损伤的解析计算公式，对船舶舷侧抗撞性结构设计和耐撞性能评估都具有一定的参考价值。

关键词：船舶碰撞；舷侧外板骨材；损伤机理；解析计算；数值仿真

在船舶海洋工程界，船舶结构抗撞性能一直是一个重要问题。船舶碰撞是船舶结构安全的主要威胁之一。严重的碰撞可能会导致船舶结构损伤，外壳破裂甚至漏油、人员伤亡等重大事故，造成巨大的经济损失，和严重的环境破坏。近些年，随着船舶吨位增大，球鼻艏的安装也越来越普遍[1]。尖锐的球鼻艏对于船侧结构威胁较大。为了将船舶因碰撞造成的损失降到最低，研究船舶舷侧结构在球鼻艏撞击下的损伤响应就显得很有意义。

Lin等[2]总结了船舶碰撞和搁浅结构响应机理的主要研究方法，包括经验方法，实验方法，有限元数值仿真方法和解析计算方法。其中解析计算方法利用塑性力学原理，通过简化分析方法推导得到有关计算公式，具有计算周期短、结构变形破坏模态易观察、结果精度较高等优点，适合应用于船舶初步设计和碰撞事故应急处理。于兆龙等[3-4]使用解析计算方法得到一系列用于船舶碰撞和搁浅过程中结构响应计算的解析计算公式。此外，数值仿真方法也被广泛应用于船舶与海洋结构物的抗撞性分析。Yamada等[5]利用仿真技术，研究了缓冲球鼻艏的性能；Yu等[6]利用LS_DYNA程序，分析了船舶搁浅场景下的结构响应。数值方法被证明是可信度较高的方法，因此可以用来验证解析计算公式的准确性。

在以往对船舶碰撞的研究中，Wang等[7-8]提出了针对板材的不同变形模式下的结构变形阻力的解析计算公式。然而在该方法中，没有考虑相关骨材的作用。骨材构件通过与板材构件焊接为一个整体从而提高结构整体的强度和刚度。传统的处理骨材的方法是Paik[9]提出的等效板厚法，即将骨材截面分摊到被依附的板上，通过增加被依附板的厚度来代替骨材的作用，这一方法对骨材的作用有明显的低估，存在一定得局限性[10]。因此，本文首先通过数值仿真技术对船舶舷侧外板上骨材的变形模态进行分析，然后运用塑性力学理论对骨材的变形损伤机理进行研究，得到骨材变形能和变形阻力的解析计算公式，并结合数值仿真结果进行了验证，所得到的成果对船舶舷侧在受球鼻艏撞击的场景下的抗撞性结构设计和耐撞性能评估都具有一定的参考价值。

1问题描述

Wang等[7-8]提出了在不考虑骨材情况下，船舶遭受球鼻艏撞击时板材的不同变形模式和结构变形阻力的解析计算公式。然而，对于实际的情况，骨材的存在对结构抵抗外载荷有显著的增强作用，是船舶舷侧结构不可缺少的组成部分，其中又尤以舷侧外板上的骨材最为重要，是本文研究的重点。典型的船舶舷侧结构主要包括：舷侧外板，舷侧纵桁，舷侧肋板，及它们的骨材。舷侧结构如图1所示。

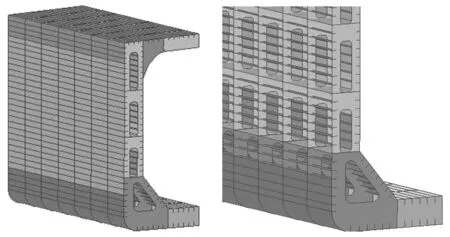
图1　船舶舷侧结构Fig.1 Model of ship side structures

在球鼻艏的撞击下，船舶舷侧外板首先发生凹陷的变形损伤，此时舷侧外板上的骨材也随着舷侧外板的变形受到挤压，从而发生拉伸和弯曲变形，形成弓字形的变形模态，如图2所示。通过数值仿真，可以观察到，由于船舶舷侧肋板的刚度较大，在未与球鼻艏发生直接接触的情况下不易发生变形，故其对骨材的两端起到了类似于刚性固定的作用，因此，骨材的变形局限于相邻的两根未发生变形的肋板之间。

图2　骨材变形模态Fig.2 The deformation pattern of stiffener

一旦当外板发生破裂，船舶舷侧的抵抗力会迅速下降，骨材将随着外板在短时间内发生破裂，自身抵抗变形的作用也大大降低，失去了研究的意义。而且当外板破裂后会发生漏水等事故，可能会造成更加严重的后果，因此在船舶设计过程中需要尽量保证船舶不会发生外板破裂的情况。因此，本文针对骨材的研究只考虑到舷侧外板发生破裂为止。

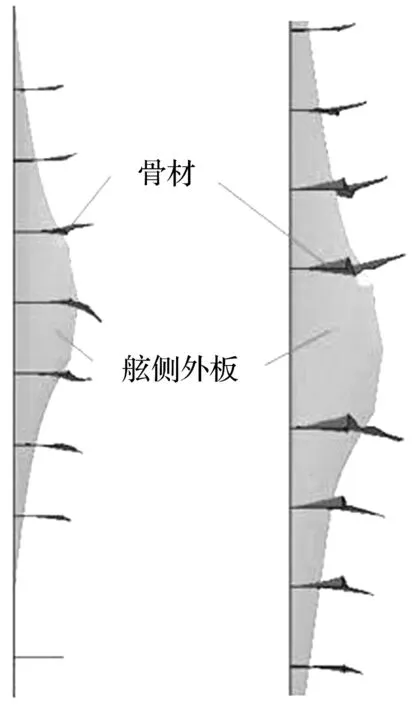
图3　骨材面内变形图(从船头看向船尾)Fig.3 The deformation pattern in plane (see from bow to stern)

由于骨材的高度与其长度相比很小，其发生的变形主要是面内变形，而不会像纵桁或者肋板一样出现受压一端向两侧偏移从而出现明显的褶皱的情况，因此，骨材在碰撞过程中的能量耗散也主要发生在面内变形上，其面内变形可从数值仿真中看出，如图3所示。

2舷侧外板骨材变形机理解析计算

2.1骨材变形损伤的几何模型

根据数值仿真模拟的结果，对骨材变形进行以下假设：

(1) 骨材的一个长边紧密地焊接在舷侧外板上，使得骨材的长边与舷侧外板同步变形；

(2) 骨材在变形过程中不发生侧向位移，发生的塑性变形是面内变形；

(3) 未与球鼻艏接触的舷侧肋板刚度较大，对骨材两端的约束视为固定约束；

(4) 骨材与其它舷侧结构之间没有相互作用的影响，在研究中单独考虑骨材的变形。

通过数值模拟和以上假设，可以建立如图4所示的骨材变形的几何模型。

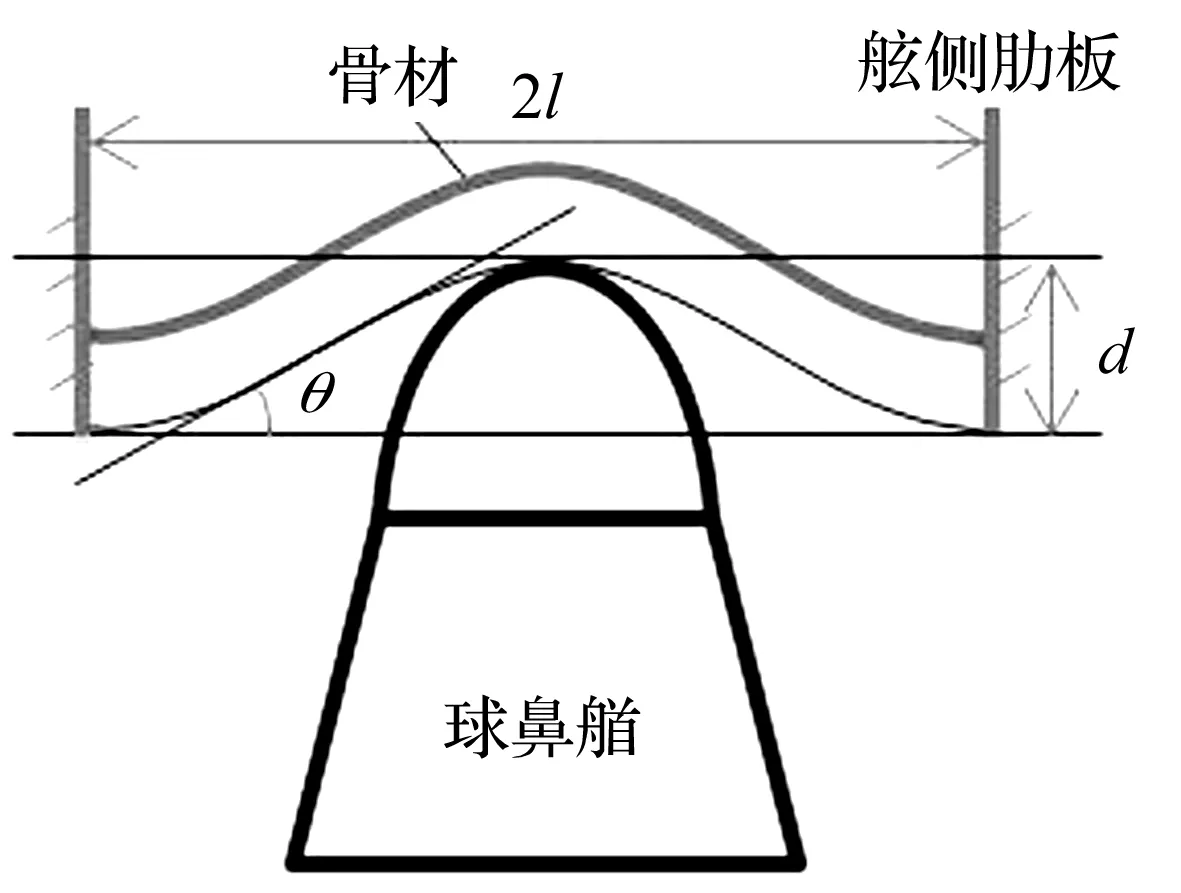
图4　球鼻艏撞击下骨材变形的理论模型Fig.4 The theoretical model of the deformed stiffener during head-on collision

图4中，未与球鼻艏接触的相邻舷侧肋板之间的距离为2l，球鼻艏的撞击深度为d。则骨材两端和中间部分发生弯曲的角度θ为：

θ≈arctan(d/l)

(1)

从图中不难看出，按式(1)得到的θ的值会比实际的值偏小，故在此引入修正因子λ=1.1～1.2。

2.2骨材的能量耗散模式

舷侧外板上的骨材变形主要分为两个部分，即固定约束在舷侧肋板上的两端部分和与球鼻艏直接接触或随着舷侧外板一同变形的中间部分。这两个部分的能量耗散有较大的区别。两端部分主要发生塑性弯曲变形，能量以弯曲变形能的形式耗散；中间部分除发生弯曲变形之外，还会发生膜拉伸变形，能量也通过这两种变形耗散。

在计算中，假设骨材的材料为理想弹塑性材料，弯曲能量Eb和膜拉伸能量Em的耗散率通过下式计算得到：

(2)

(3)

(4)

N0=σ0Hs

(5)

2.3骨材两端弯曲变形能量耗散

在左右两端处，骨材在球鼻艏的冲击下，形成如图4所示的弧形变形，弯曲变形是该部位最主要的变形模态，其中一端因弯曲变形而产生的能量耗散率为：

(6)

E1=Eb1=M0tθ

(7)

式中：t为骨材的厚度。

2.4骨材中部能量耗散

骨材中间部分，能量耗散模式主要包括塑性弯曲能量耗散和膜拉伸能量耗散。对于与球鼻艏直接接触的骨材，其因变形损伤而耗散的能量，在总的能量中占较大的比例，在碰撞过程中，骨材受到球鼻艏的挤压不断发生弯曲变形，此外，球鼻艏与舷侧外板的接触力很大从而引起较大的摩擦力，引起骨材的膜拉伸变形。同时摩擦力改变了材料的极限屈服极限，使得极限弯矩发生变化，塑性弯曲变形的能量也有所不同。轴向拉力和弯矩共同作用下的极限屈服条件如图5所示。

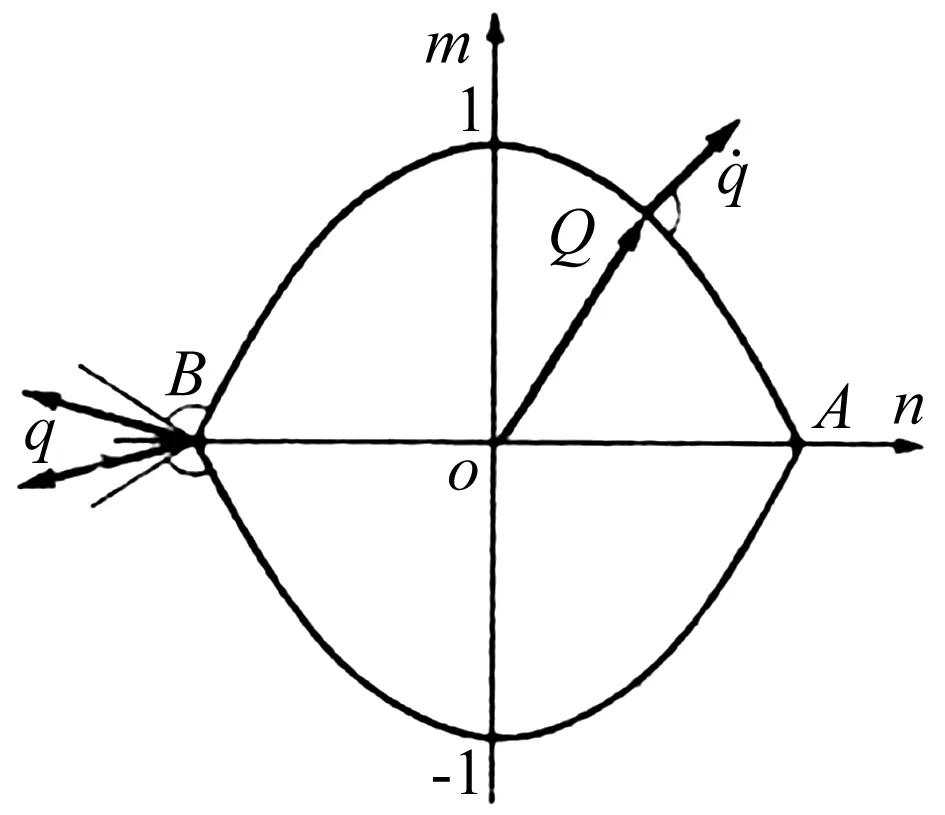
图5　拉力和弯矩共同作用下的极限屈服条件曲线Fig.5 The ultimate condition under the combined effects of the bending moment and the axial forces

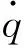
(8)

式中，M0和N0分别为弯矩和拉力单独作用下的极限弯矩和极限拉力，M和N为弯矩和拉力联合作用下的极限弯矩和极限拉力。

因此，单位厚度骨材的中间部分的一半的能量耗散率为：

(9)

式中,N为单独一根骨材所受的膜拉伸力，其数学表达式为：

(10)

式中,P为单独一根骨材对球鼻艏的抵抗力，μ为球鼻艏与舷侧外板之间的摩擦因数，值得注意的是N的取值在任何条件下都不能大于N0，如果出现N>N0的情况，则令N/N0=1。总的抵抗力取用等效板厚法算得的舷侧外板抵抗球鼻艏挤压的抵抗力， Wang等[7-8]根据球鼻艏的形状提出了两种舷侧外板抵抗撞击的模型。

(1) 球鼻艏视为点载荷，圆板的变形模型如图6所示：

F=πσ0ted

(11)

式中，te是等效板厚；

(2) 球鼻艏视为刚性球，圆板的变形模型如图7所示：

F=πσ0teR1sinθ(1+(r/R1)sinθ)

(12)

式中，R1为板变形区域半径，r为刚性球的半径。

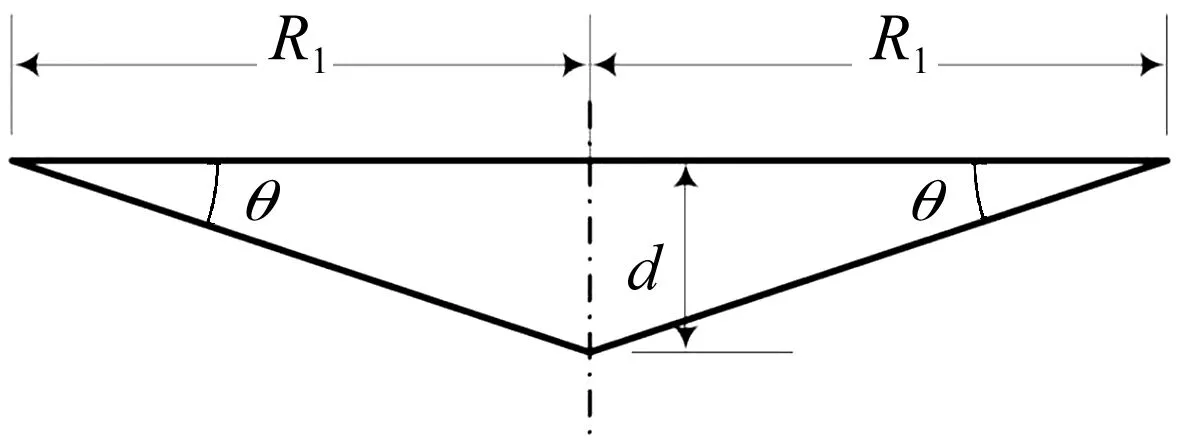
图6　圆板遭受点载荷撞击变形模型Fig.6 Circular plate subjected to a point load

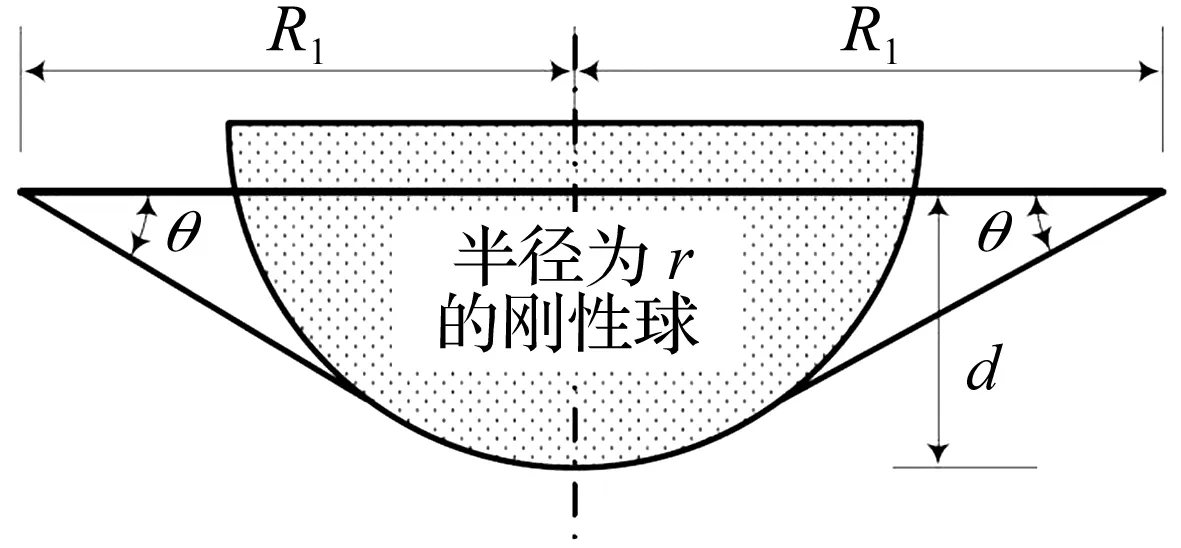
图7　圆板遭受刚性球撞击变形模型Fig.7 Circular plate subjected to punching of a rigid sphere

由于外板破裂后，对骨材的变形研究失去了意义，故需要准确预测外板发生破裂时球鼻艏的撞击深度，Gao等[11]提出了外板破裂时的球鼻艏的最大撞深为：

(13)

式中，c为经验因子取0.5～0.6，εc为材料的拉伸塑形应变，通常取0.2～0.35。

根据上述极限屈服条件，将参数无因次化得到：

(14)

根据正交性规则，有：

(15)

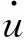
(16)

将式(15)代入式(9)中可得：

(17)

故与球鼻艏直接接触的骨材的中间部分的一半的变形能量为：

18)

对于未与球鼻艏直接接触而是随着外板的变形而发生变形的骨材，其因变形损伤耗散的能量占总能量的比例较小，在变形过程中，膜拉伸力取N0，主应变为：

u=(l/cosθ-l)/l=1/cosθ-1

(19)

则这类骨材在变形过程中中间部分的一半的能量耗散为：

(20)

能量耗散率为：

(21)

综上，骨材在遭受球鼻艏撞击过程中总的变形能为：

(22)

或

(23)

2.5骨材的抵抗力

通过以上对骨材变形损伤机理的研究，已经建立了舷侧外板骨材的能量耗散解析式。则总的能量耗散率为：

(24)

或

(25)

球鼻艏撞深的表达式为：

d=ltanθ

(26)

撞击速率为：

(27)

故骨材对球鼻艏的抵抗力为：

(28)

或

(29)

3数值仿真验证

3.1数值仿真模型

本文采用球鼻艏船舶撞击双壳油轮舷侧场景验证解析模型的合理性。被撞击船舶主尺度见表1，由于撞击的局部性，被撞击船舶只对舷侧一部分进行建模，其有限元模型如图1。被撞击船舶有限元模型材料采用理想弹塑性材料，弹性模量为2.1×1011N/m2，密度为7 850.0 kg/m3，泊松比为0.3，撞击位置的舷侧结构均采用普通钢材料，屈服应力为235 N/mm2。

研究中，撞击船选取的是带有球鼻艏的62200DWT油轮，其主尺度见表1。本文中撞击船的球鼻艏设置为刚性体，在撞击过程中不发生变形，撞击船球鼻艏与被撞击船舷侧外板之间的摩擦系数为0.3。撞击船有限元模型见图8。

表1　被撞船及撞击船主尺度表

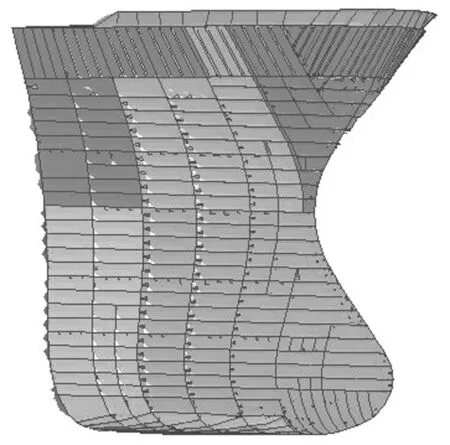
图8　撞击船艏有限元模型Fig.8 Model of the bow of striking ship

3.2撞击场景设计

撞击船撞击速度为5 m/s，正向撞击被撞击船舷侧。撞击位置选取两个：工况1：撞击点位于被撞击船舷侧两相邻肋框和两相邻舷侧纵桁围城的矩形的中心处；工况2：撞击点位于两相邻肋框中点处的舷侧纵桁上。具体位置见图9。

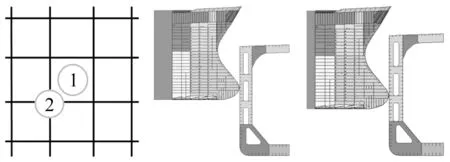
图9　撞击位置示意图Fig.9 The collision positions

4解析计算结果验证与讨论

4.1工况1计算结果

当球鼻艏撞击在位置①时，根据已知的球鼻艏尖端的平均半径和舷侧外板上骨材的间距，可知中间的三根骨材会遭受到球鼻艏的直接冲击，两边的四根骨材则会随着舷侧外板的变形而发生变形，如图3中的左侧图所示，与球鼻艏直接接触的三根骨材其能量耗散采用式(22)进行计算，间接受到球鼻艏影响的四根骨材其能量耗散采用式(23)进行计算。当球鼻艏刚接触到舷侧外板时，只有一根骨材参与抵抗球鼻艏的冲击而发生变形，随着撞深的增加，参与抵抗球鼻艏冲击的骨材逐渐增多，当舷侧外板发生破裂时，球鼻艏未能与舷侧纵桁和肋板发生接触，故骨材的变形损伤始终限制在相邻的肋板框架内，如图2所示。

工况1中数值仿真和理论计算得到的变形能量随撞击深度变化的对比曲线如图10所示。从图中可以看出，数值计算得到的结果和解析方法计算得到的结果吻合良好。在撞深达到1.05 m时，数值计算得到的曲线有一段平缓的过度，这是因为在这个时候，虽然舷侧外板还没有发生破裂，但变形损伤最严重的一根骨材已经发生了撕裂，此时它的抵抗力可以忽略。

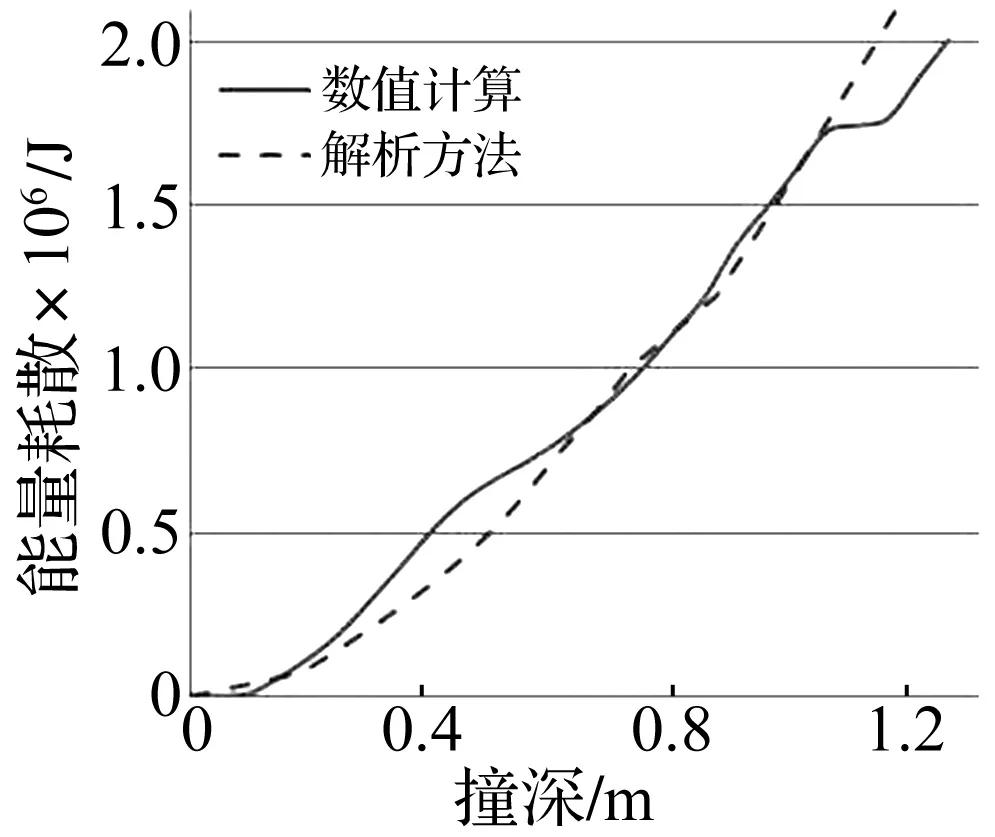
图10　工况1中能量-撞深关系曲线对比图Fig.10 The comparison of energy-depth relationship in case 1

4.2工况2计算结果

当球鼻艏撞击在位置②时，根据已知的球鼻艏尖端的平均半径和舷侧外板上骨材的间距，可知中间两根骨材会遭受到球鼻艏的直接冲击，两边的八根骨材则会随着舷侧外板的变形而发生变形，如图3中的右侧图所示，与球鼻艏直接接触的两根骨材其能量耗散采用式(22)进行计算，间接受到球鼻艏影响的八根骨材其能量耗散采用式(23)进行计算。当球鼻艏刚接触到舷侧外板时，只有舷侧纵桁和肋板构成的十字结构受到球鼻艏的冲击作用，骨材没有参与，随着撞深的增加，参与抵抗球鼻艏的骨材出现并逐渐增多。在这种情况下，骨材的变形区域不再像工况1中一样局限于一个肋位之间，由于被撞击肋板的严重受损，其对骨材的限制大大降低，根据之前的假设，可以忽略肋板对骨材的作用，骨材的变形模态和工况1以及本文提出的解析模型之间并无差异，只是骨材的变形扩大到了两个肋位之间，如图11所示。

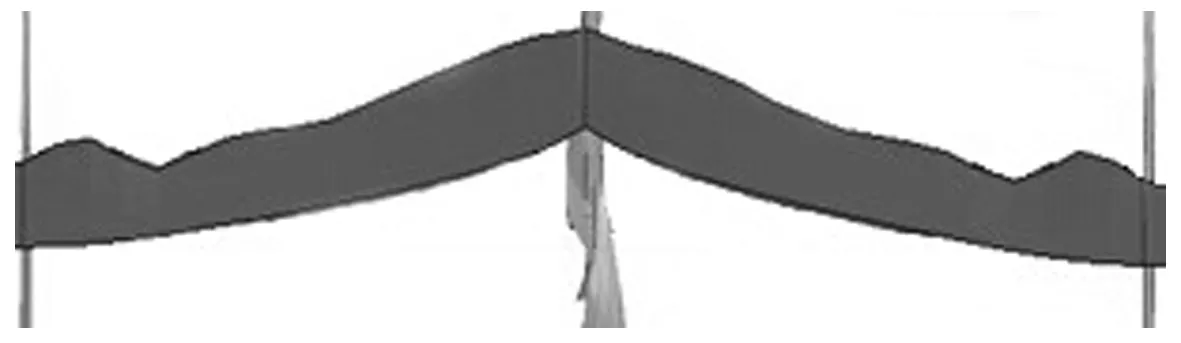
图11　工况2骨材变形模态Fig.11 The deformation pattern of stiffener in case 2

工况2中数值仿真和理论计算得到的变形能量随撞击深度变化的对比曲线如图12所示。从图中我们可以看出，数值计算得到的结果和解析方法编程计算得到的结果吻合良好。当撞深未达到0.18 m之前，球鼻艏未接触到骨材，故这段撞深内骨材的能量耗散很小。此后一段距离内，解析方法计算得到的骨材的能量耗散较数值计算得到的结果较大，这是因为在解析方法中，忽略了肋板的作用，而实际上，肋板在刚接触到球鼻艏时，变形损伤还并不严重，此时它对骨材的变形还有一定得限制作用，骨材的变形在肋板的限制下不会很大。此后，两种方法的结果几乎一致，在撞深达到1.05 m时，变形损伤最严重的两根骨材发生了一定的破裂，造成了和工况1中类似的情况。

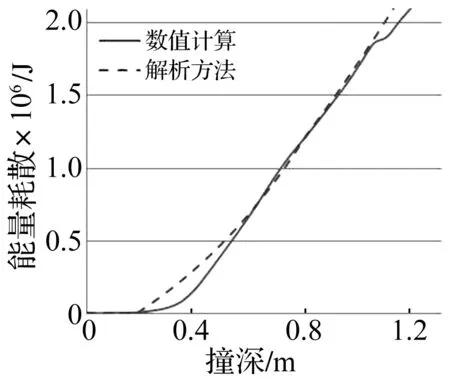
图12　工况2中能量-撞深关系曲线对比图Fig.12 The comparison of energy-depth relationship in case 2

5结论

本文主要研究了船舶舷侧遭到球鼻艏撞击时，舷侧外板上骨材的变形损伤机理。通过对数值仿真中骨材变形损伤过程的观察研究，提出了骨材变形的理论模型。

骨材在球鼻艏的冲击下发生弧状的塑性变形，其变形损伤主要包括两个部分：

(1) 是受到舷侧肋板约束的两端部分，这部分的能量主要通过弯曲变形的形式耗散；

(2) 是与球鼻艏直接接触或者因舷侧外板的变形而间接受迫变形的中间部分，这部分的能量主要通过弯曲变形和膜拉伸变形共同作用的形式耗散。本文应用塑性力学原理和数值仿真，对这两部分能量耗散分别进行了研究，建立起了骨材能量耗散和抵抗力的解析计算公式，并与数值计算的结果进行对比分析，结果吻合良好。

骨材数量众多，依附在舷侧外板上会明显加强舷侧外板的刚度，以抵抗外来的冲击，在评估船舶的抗撞性能时，不可对其进行忽略也不宜运用等效板厚法来对其进行简单的处理，本文对骨材的变形机理进行了详细的分析， 所得到的解析计算公式对船舶舷侧的抗撞性结构设计和耐撞性能评估都具有一定的参考价值。

参 考 文 献

[1] Lin Hong, Amdahl J, Wang Ge. A direct design procedure for FPSO side structures against large impact loads[J]. Journal of Offshore Mechanics and Arctic Engineering, 2009, 131:031105.

[2] Lin Hong. Simplified analysis and design of ships subjected to collision and grounding[D]. Trondheim:Norwegian University of Science and Technology, 2008.

[3] 于兆龙，胡志强，王革,等. 船舶搁浅于台型礁石场景下双层底纵桁上纵骨变形机理研究[J]. 振动与冲击，2014，33(3)：162-169.

YU Zhao-long, HU Zhi-qiang, WANG Ge, et al. Collapse mechanism of longitudinal web girder attached stiffeners in a shoal grounding scenario of double bottom tanker[J]. Journal of Vibration and Shock, 2014, 33(3): 162-169.

[4] 于兆龙，胡志强，刘毅,等. 船舶搁浅于台型礁石场景下双层底肋板骨材变形机理研究[J]. 振动与冲击，2014，33(14)：188-194.

YU Zhao-long, HU Zhi-qiang, LIU Yi, et al. Collapse mechanism analysis of stiffeners on transverse floors in a shoal grounding course of double bottom tanker[J]. Journal of Vibration and Shock, 2014, 33(14): 188-194.

[5] Yamada Y, Endo H. Experimental and numerical study on the collapse strength of the bulbous bow structures in oblique collision[J]. Marine Technology, 2008, 45(1):42-53.

[6] Yu Zhao-long, Hu Zhi-qiang, Amdahl J, et al. Investigation on structural performance predictions of double-bottom tankers during shoal grounding accidents[J]. Marine Structures, 2013, 33:188-213.

[7] Wang Ge. Structural analysis of ships’ collision and grounding[D]. Tokyo: University of Tokyo, 1995.

[8] Wang Ge, Arita K, Liu D. Behavior of a double hull in a variety of stranding or collision scenarios[J]. Marine Structures, 2000, 13(3): 147-187.

[9] Paik J K. Cutting of a longitudinally stiffened plate by a wedge[J]. J Ship Res, 1994, 38(4): 340-380.

[10] 刘毅，王晋，胡志强．船舶搁浅于台型礁石中的等效板厚法的研究[J]．工程力学，2013，30(8)：287-293.

LIU Yi, WANG Jin, HU Zhi-qiang. Investigation on smeared thickness method for ship grounding over obstacles with large contact surfaces and trapezoidal cross section[J]. Engineering Mechanics, 2013, 30(8): 287-293.

[11] Gao Zhen-guo, Hu Zhi-qiang, Wang Ge, et al. An analytical method of predicting the response of FPSO side structures to head-oncollision[J]. Ocean Engineering, 2014, 87:121-135.

Analyical prediction method for crashworthiness of side shell stiffeners

SUN Bin1, HU Zhi-qiang1, WANG Jin1,2

(1. State Key Lab of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. COTEC USA, Houston 77079, USA)

Abstract:A theoretical model for analysing the damage mechanism of stiffeners on the outer plating of ship side shell under the scenario of striking by a bulbous bow was proposed. It is based on a study of the progressive process of structural deformation and the plastic-elastic theory. The research stresses on establishing the characteristic deformation mechanism and identifying the major energy dissipation pattern of the stiffeners attached on side shell plating. The analytical expressions of distortion energy of stiffeners and average deformation resistance were derived. The analytical method was verified by numerical simulations using code LS-DYNA. The results of numerical simulations and those by the proposed analytical method match well. The proposed analytical method can be used for the quick assessment of performances of ship side structures during ship collision.

Key words:ship collision; stiffeners on side shell plating; structural damage; simplified analytical method; numerical simulation

基金项目：国家自然科学基金项目(51239007)

收稿日期：2014-10-22修改稿收到日期：2015-04-20

通信作者胡志强 男，博士，副教授，1975年生

中图分类号:U661.7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.010

第一作者 孙斌 男，研究生，1991年生