含负电容谐振分流电路的压电声子晶体梁的局域共振带隙与振动衰减

陈　良, 杜红军， 王　刚, 张　浩

(1. 空军第一航空学院 航空机械工程系，河南 信阳　464000；2. 湖南大学 机械与运载工程学院，长沙　410082；3.国防科技大学 装备综合保障重点实验室，长沙　410073)

含负电容谐振分流电路的压电声子晶体梁的局域共振带隙与振动衰减

陈良1, 杜红军1， 王刚2, 张浩3

(1. 空军第一航空学院 航空机械工程系，河南 信阳464000；2. 湖南大学 机械与运载工程学院，长沙410082；3.国防科技大学 装备综合保障重点实验室，长沙410073)

摘要：通过在树脂梁上周期贴敷压电片，并连接由被动电阻-电感(RL)谐振分流电路和负电容(NC)电路串联而成的分流电路，构造了压电声子晶体梁结构。采用传递矩阵法计算了该类型压电声子晶体梁结构的带隙特性，并对电阻、电感和负电容对局域共振带隙的影响进行了深入分析，发现分流电路中的LC电磁振荡回路可产生局域共振带隙，而串联的负电容电路则可增强压电片的机电耦合效率，从而增强带隙衰减范围和衰减幅值。采用振动实验方法对理论分析结果进行了验证，证实串联的负电容对局域共振带隙的增强作用，为局域共振声子晶体的设计提供了新的思路。

关键词：声子晶体；压电分流；负电容；局域共振

声子晶体作为一种人工周期结构在近十几年时间里引起了科研工作者的广泛关注。声子晶体具有带隙特性，可以抑制带隙频率范围内的弹性波传播，因此，在减振降噪、声波滤波器、新型换能器等方面具有广泛的应用前景[1]。

然而，对于传统的声子晶体，当其组分和结构参数被确定后，带隙的频率范围即被确定，无法改变。随着智能材料的发展，智能材料被引入到声子晶体中，以实现带隙可调的智能型结构。其中，通过引入压电材料及分流电路而构建的压电分流阵列是实现智能型声子晶体中一种很有前景的方法。Thorp等[2]首次将电阻及电感谐振型压电分流电路引入到声子晶体结构中。随后具有压电分流电路的周期结构中的弹性波传播特性受到广泛研究[3-5]。然而，基于电阻-电感(RL)等被动元件压电分流电路的声子晶体的局域共振带隙非常窄，带隙衰减也较小。为了获得宽频局域共振带隙，Airoldi等[6]引入了具有多谐振模态的分流电路,但电路比较复杂且带隙的衰减幅度仍有待提升。最近，负电容分流技术被认为是一种简单却高效的拓宽Bragg带隙的新方法[7]。Chen等[8]提出了具有负电容(NC)分流电路的一维声子晶体梁的分析模型。Casadei等[9]研究了分别连接负电容电路和被动RL分流电路的悬臂板的振动特性，但负电容分流电路和RL分流电路被连接的不同的压电片上，结构形式较为复杂。Zhang等[10]从理论上分析了并联负电容谐振分流电路的声子晶体梁结构的弯曲波带隙特性。

本文从理论和试验两方面深入研究了含串联负电容谐振分流电路(SNCRL)的声子晶体梁结构的局域共振带隙特性。其中，分流电路中的LC电磁振荡回路被用于产生局域共振带隙，而串联的负电容电路则被用来增强压电片的机电耦合效率，从而增强局域共振带隙。传递矩阵法被用于压电分流声子晶体梁结构的带隙特性计算，并对电阻、电感和负电容对局域共振带隙的影响进行了深入分析。最后本文搭建了振动实验系统，采用振动实验方法对文中理论分析结果进行了验证，证实了RL分流电路可使声子晶体梁产生局域共振带隙，而负电容则对局域共振带隙具有增强作用。

1声子晶体梁的物理建模

如图1所示，在基体梁上周期性对称特贴敷压电陶瓷(PZT)片，形成一维声子晶体梁。每一组成对贴敷的两片压电片的极化方向相反，电极并联，并与分流电路相连。分流电路由电阻R，电感L和电容Cn串联而成。图中，梁上贴有压电片的部分用A表示，未贴压电片的部分用B表示。

压电片的极化方向为z轴方向，除去沿x轴方向受力外，其余表面均自由。设对应于坐标轴x,y,z的方向在压电方程中分别用1,2,3表示，则d型压电方程可以简化为[9]

(1)

每组压电片外接分流电路的电阻抗为：

(2)

式中：s为Laplace算子,R、L和Cn分别为电阻、电感和电容的值。

由基本电学公式，可得分流电路中的电流为：

(3)

式中：V为压电片两电极之间的电势差，Q为电荷。

压电片内电场与电极上的电势差之间的关系为：

V=E3hp

(4)

式中：hp为压电片的厚度。

若采用精确积分方法[11]求解电极上的电荷，那么电极上的电荷Q为：

Q=∬AsD3ds

(5)

式中：As为压电片的表面面积。

将式(1)代入到式(5)得：

(6)

对于声子晶体梁中传播的弯曲波ψ(x,t)，压电片x处的应变可以表示为：

(7)

式中：hb为基体梁的厚度。

将式(7)代入式(6)，积分得：

(8)

联立式(3) ，(4) ，(8)，解得：

(9)

最后，将式(9)代入式(1)可得：

(10)

式中：

(11)

从式(10)和式(11)可以看出，分流电路对压电片的作用等效于在压电片各个位置保持一个大小相同，只随时间变化的附加应力。

如图1所示的声子晶体梁，忽略剪切变形和截面绕中心轴转动惯量对弯曲振动的影响，采用Euler-Bernoulli梁模型，其弹性波波动方程为[12]：

(12)

式中：ψ(x,t)表示x处质点t时刻的横向位移。E和I分别为声子晶体梁在x处的弹性模量、横截面惯性矩。ρ和A分别为声子晶体梁在x处密度和横截面面积。

将基体梁和压电片参数代入式(12)则可以得到声子晶体梁中第n个原胞中A，B段的弹性波波动方程：

(13)

式中：ψn,A(x,t)，ψn,B(x,t)分别为声子晶体梁第n个原胞中A，B段的横向位移。Eb和Ep分别为基体梁和压电片的弹性模量，Ib和Ip分别为基体梁和压电片的横截面惯性矩。ρb和ρp分别为基体梁和压电片的密度，Ab和Ap分别为基体梁和压电片的横截面面积。

设其中的弯曲波为频率ω的简谐波，即：

(14)

式中：ψn,A(x)、ψn,B(x)为振动幅值。

将式(14)代入式(13)，则可以化为四阶线性常微分方程，求解得：

(15)

式中，An,1,An,2,An,3,An,4,Bn,1,Bn,2,Bn,3和Bn,4为待定系数，λi为波数，可以表示为[8]：

(16)

在元胞n中，不同组元A、B的边界处位移、转角、弯矩和剪力连续条件为：

(17)

将式(14)代入式(17)，并整理为矩阵形式:

H1An=K1Bn

(18)

Bn=[Bn,1Bn,2Bn,3Bn,4]T。

同理，在元胞n和n-1之间的边界处位移、转角、弯矩和剪力连续条件为：

式中：l=lb+lp为晶格常数。

将式(14)代入式(19)，并整理为矩阵形式：

H2An=K2Bn-1

(20)

联立式(18)和式(20)，可得：

Bn=TBn-1

(21)

式中，T为改进积分建模方法得到的传递矩阵，可以表示为：

T=K1-1H1H2-1K2

(22)

对于图1所示的无限周期声子晶体梁结构，由其在x轴方向的周期性，根据Bloch定理[14]可得：

Bn=eμBn-1

(23)

式中：μ=α+iβ为波传播常数，实部α为衰减常数，虚部β为相位常数。

那么，联立式(21)和式(23)可以得到特征值方程：

(24)

I为单位矩阵，对于给定的频率ω，由式(24)可以计算传播常数μ。当频率ω位于某些频率范围内时，若α=0，那么弹性波可以在声子晶体梁中无衰减的传播，意味着该频率处于通带内；若α≠0，那么弹性波在声子晶体梁中传播发生衰减，意味着这些频率范围形成带隙，α越大则弹性波衰减幅度越大。

2数值计算

对于具有无限周期的声子晶体梁，传播常数可以用来描述其波传播特性。作为例子，基体梁材料选用环氧树脂，压电陶瓷片为PZT-5H，其材料参数和结构参数分别如表1和表2所示。

表1　基体梁所用材料参数和结构参数

表2　压电片所用材料参数和结构参数

2.1梁的带隙结构

由以上参数计算得到声子晶体梁的带隙结构如图2所示。图中细实线是电路短路(L=0，Cn=0，R=0)时梁的带隙结构，此时无局域共振带隙，只有由压电片和基体梁的阻抗失配引起的Bragg带隙。图中点线是RL电路(L=0.44 H，Cn=0，R=50 Ω)时梁的带隙结构，此时分流电路的电磁振荡作用产生局域共振带隙。粗实线为串联负电容谐振(SNCRL)电路(L=0.1 H，Cn=-1.3Cp=-234 nF，R=50 Ω) 时梁的带隙结构，此时有局域共振带隙，且相比于RL电路，其局域共振带隙得到了增强。综上可以发现：RL电路能使声子晶体梁产生局域共振带隙，而在RL电路中串联负电容能有效增强局域共振带隙，提高带隙内的衰减和增大带隙宽度。

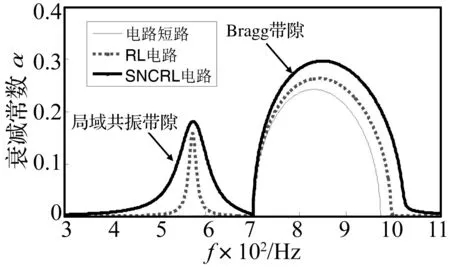
图2　声子晶体梁的带隙结构Fig.2 Band gaps of phononic crystal beam

2.2电阻、电感和负电容对局域共振带隙的影响

2.2.1电阻对局域共振带隙的影响

图3为局域共振带隙随电阻R的变化关系曲线(此时设定Cn=0，L=0.44 H)。从图中可以看出，随着电阻的增大，局域共振带隙内最大衰减幅值逐渐减小，而带隙位置保持不变。衰减幅值减小的原因是电阻的增大会使得分流电路的电磁振荡作用减弱。

兰德通过商业管理创新来帮助美国军事物流实现现代化，这些研究为国防部节省了数百万美元，同时提高了军队战斗力。

图3　带隙随电阻的变化Fig.3 Band gaps’ variation with the resistance

2.2.2电感对局域共振带隙的影响

图4为局域共振带隙随电感L的变化关系曲线(此时设定Cn=0，R=50 Ω)。从图中可以看出，随着电感值的增大，局域共振带隙的位置向低频移动。其原因是随着电感值的增大，分流电路的谐振频率fr逐渐变小，从而导致局域共振带隙的频率往低频移动。

(25)

图4　带隙随电感的变化Fig.4 Band gaps’ variation with the inductance

2.2.3负电容对局域共振带隙的影响

(26)

由式(26)可知，串联负电容的作用等效于增大压电片的固有电容Cp。随着负电容幅值的增大，谐振电路中的总电容值(CpCn)/(Cp+Cn)减少。如保持电路电感值不变，随着负电容幅值的增大，分流电路的谐振频率会升高。为分析负电容对局域共振带隙的影响，根据式(26)分别调节负电容Cn和分流电感L的取值，以保持电路的谐振频率fr不变，得到局域共振带隙随负电容的变化关系曲线。

从图5中可以看出，随着负电容幅值的减小,局域共振带隙增强效果越好，且负电容幅值越接近压电片固有电容时，局域共振带隙增强效果越好。

图5　带隙随负电容的变化Fig.5 Band gaps’ variation with the negative capacitance

3实验

3.1大值电感和负电容的实现

为实现较低频的局域共振带隙，谐振分流电路中的电感L需要取较大的值；但为了同时实现较大的局域共振衰减，电路中的电阻R不能太大。常用的绕线电感器难以在自身电阻较小的情况下实现较大的电感值，难以满足需要。所以实验中采用Antoniou’s电路[15]来模拟大值电感。Antoniou’s电路如图6(a)所示，其等效电感由式(27)计算，可通过改变电阻参数进行调节。

(27)

实验中设计的模拟电路采用的运算放大器为OPA445AP，其最大工作电压为±45 V，其他各元器件参数为R1=R2=10 kΩ，R3=1 kΩ，R4为取值范围为0～10 kΩ的可调电阻，C1=220 nF，那么利用式(27)计算该电路的模拟电感L的取值范围为0～2.2 H。

负电容模拟电路如图6(b)所示，该电路[16-17]的等效电容值可表示为：

(28)

(a) Antoniou’s电路　　　(b) 负电容模拟电路图6　模拟电路Fig.6 Synthetic circuit

3.2实验结果

为了验证被动RL分流电路能够产生局域共振带隙和负电容对局域共振带隙的增强作用，设计实验测试方案和实验测试系统分别如图7和图8所示。图7中，激振器(B&K4824)对梁A点进行激励，采用Polytec激光扫描测振系统(PSV-500)测量A点和B点的振动速度，分别记为VA，VB，从而得到A、B两点之间的振动速度传输特性T为：

(29)

实验中使用的样品梁共8个周期，晶格常数为0.08 m,总长为0.64 m。基体梁和压电片的几何参数和材料参数与数值计算的参数一样，参见表1和表2。根据图7搭建的实验测试系统如图8所示，利用细绳对实验样品进行悬挂，模拟横向自由边界条件，激振器输入为0～2 kHz的白噪声。当接入为RL谐振分流电路时，调节电路参数使电感L=0.44 H，电阻R=50 Ω；当接入为串联负电容谐振分流电路(SNCRL)时，调节电路参数使电感L=0.1 H，电阻R=50 Ω，负电容Cn=-1.3Cp=-234 nF。

图7　实验测试方案Fig.7 Experimental measurement scheme

图8　实验测试系统Fig.8 Experimental measurement system

图9　实验测试与理论分析结果Fig.9 Experimental measurement results and theoretical analysis results

实验测得的A、B两点的振动速度传输特性曲线如图9(a)所示，其中细实线，点线，粗实线分别表示分流电路短路，RL谐振分流电路,串联负电容谐振分流电路(SNCRL)时的速度传输特性曲线。从图9(a)中可以看出,在局域共振带隙中心频率572 Hz附近处，RL谐振分流电路声子晶体梁的衰减频段为556～589 Hz，衰减带宽为33 Hz，最大衰减幅值为7 dB；而串联负电容谐振分流电路声子晶体梁的衰减频段为541～604 Hz，衰减带宽为63 Hz，最大衰减幅值达13 dB。

图9(b)为理论分析结果(同图2)，为了方便对比分析实验结果和理论结果。从实验测试结果可以发现RL谐振电路的确能使声子晶体梁产生局域共振带隙，而在RL谐振电路中串联负电容能有效增强局域共振带隙，从而证明了理论分析的正确性。

此外，需要说明的是，虽然实验测试结果较好的验证了相应的理论分析结果，但是实验测试结果在带隙频率范围、衰减幅度等方面也存在少许误差。产生这些误差的主要原因有：① 理论计算时的模型是无限周期结构，衰减系数表征的是其带隙衰减特性；而实验测试时的样件是有限周期结构，具有自身的模态特性。实验测试得到的振动传输特性曲线将体现为模态特性和带隙特性的综合效果(如带隙范围内的模态峰被明显抑制)；② 计算中未考虑结构的阻尼，这些阻尼常常是非线性的，而且较难测量；③ 材料参数和电路参数的误差。

4结论

通过对具有压电分流电路的声子晶体梁的理论建模分析和实验验证，可以得到如下结论：

(1) 具有压电分流电路的声子晶体梁的带隙由布拉格带隙和局域共振带隙组成。当RL谐振电路中电感为零时，无局域共振带隙；当RL谐振电路中电感值不为零时，由于分流电路的电磁振荡作用形成局域共振带隙；在RL谐振电路中串联负电容能有效增强局域共振带隙，提高带隙内的衰减和增大带隙宽度。

(2) 随着分流电路中电阻的增大，局域共振带隙的衰减幅值减小而衰减范围变宽；随着电感的增大，局域共振带隙向低频移动；随着负电容幅值的减小，局域共振带隙增强效果越好。

具有压电分流电路的声子晶体梁与传统机械振子局域共振声子晶体梁相比，具有附加质量小、带隙主动可调等优点。总之，本文的研究结论为局域共振声子晶体的设计提供了新的思路。

参 考 文 献

[1] 温熙森．光子/声子晶体理论与技术[M]．北京：科学出版社,2006

[2] Thorp O, Ruzzen M, Baz A. Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches[J].Smart Material and Structrues,2001,10(5):979-989.

[3] Spadoni A, Ruzzene M, Cunefare K. Vibration and wave propagation control of plates with periodic arrays of shunted piezoelectric patches [J]. Journal of Intelligent Material Systems and Structures, 2009, 20(9): 979-990.

[4] Wang G, Chen S B, Wen J H. Low-frequency locally resonant band gaps induced by arrays of resonant shunts with Antoniou’s circuit: experimental investigation on beams [J]. Smart Materials and Structures, 2011, 20(4):015026.

[5] Dai L X, Jiang S, Lian Z Y, et al. Locally resonant band gaps achieved by equal frequency shunting circuits of piezoelectric rings in a periodic circular plate [J].Journal of Sound and Vibration,2015,337:150-160.

[6] Airoldi L, Ruzzene M. Wave propagation control in beams through periodic multi-branch shunts [J]. Journal of Intelligent Material Systems and Structures, 2011, 10(6): 1567-1578.

[7] Collet M, Ouisse M, Ichchou M N, et al. Semi-active optimization of 2D wave dispersion into shunted piezo-composite systems for controlling acoustic interaction[J]. Smart Materials and Structures, 2012, 21(4):094002.

[8] Chen S B, Wen J H, Yu D L, et al. Band gap control of phononic beam with negative capacitance piezoelectric shunt[J].China Physics B,2011,20(1):014301.

[9] Casadei F, Beck B S, Cunefare K A, et al. Vibration control of plates through hybrid configurations of periodic piezoelectric shunts [J]. Journal of Intelligent Material Systems and Structures, 2012,23(10): 1169-1177.

[10] Zhang H, Wen J H, Chen S B, et al. Flexural wave band-gaps in phononic meta-material beam with hybrid shunting circuits [J].China Physics B, 2015, 24(3):036201.

[11] Chen S B, Wen J H, Wang G, et al. Improved modeling of rods with periodic arrays of shunted piezoelectric patches [J]. Journal of Intelligent Material Systems and Structures, 2012, 23(6): 1613-1621.

[12] Meirovitch L. Fundamentals of vibrations [M]. New York: McGraw-Hill Co, 2001.

[13] 李凤明,汪越胜.压电周期结构振动主动控制研究[J].机械工程学报，2004，17(增刊2): 828-830.

LI Feng-ming, WANG Yue-sheng. Active vibration control of the piezoeletric periodic structure [J].Journal of Mechanical Engineering, 2004，17(Sup2): 828-830.

[14] Ashcroft N W, Mermin N D. Solid State Physics [M].Philadelphia, PA: Sasunders, 1976.

[15] Antoniou A. Realization of gyrators using operational amplifiers and their use in RC-active-network synthesis [J]. Proc IEEE, 1969, 116(2):1838-1850.

[16] Tang J, Wang K W. Active-passive hybrid piezoelectric networks for vibration control: comparisons and improvement [J]. Smart Materials and Structures, 2001, 10(4): 794-806.

[17] 马小路，裘进浩，季宏丽.负电容在主动-被动混合压电振动控制中的应用[J].华南理工大学学报，2012,3(40),107-112.

MA Xiao-lu, QIU Jin-hao, JI Hong-li. Application of negative capacitance to active-passive hybrid piezoelectric vibration control [J].Journal of South China University of Technology, 2012,3(40),107-112.

Local resonance band gaps and corresponding vibration attenuations of a piezoelectric phononic beam consisting of negative capacitor based resonant circuits

CHEN Liang1, DU Hong-jun1, WANG Gang2, ZHANG Hao3

(1. Department of Aeronautical Mechanical Engineering, The First Aeronautical College of Air Force,, Xinyang 464000, China;2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;3. Laboratory of Science and Technology on Integrated Logistics Support, National University of Defense Technology, Changsha 410073, China)

Abstract:Periodic arrays of piezoelectric patches connected with serial negative capacitive-resistive-inductive (SNCRI) circuits were attached to an epoxy beam so as to construct a piezoelectric phononic beam structure. The band-gap structure of the piezoelectric phononic beam was analysed with the transfer matrix approach. Subsequently, the influences of the resistance, inductance and negative capacitance parameters on local resonance band-gap were discussed. It is found that the LC oscillator circuit can lead to local resonance band-gap, and the negative capacitive circuits can enhance the electromechanical coupling efficiency of piezoelectric patches, i.e. the attenuation in the local resonance band-gap is enlarged thereby. Vibration experiments were conducted to validate the theoretical predictions, and considerable gap enhancements by negative capacitance were observed. The work provides a new way in the design of phononic crystals with tunable band gaps.

Key words:phononic crystal; piezoelectric shunting; negative capacitance; local resonance

基金项目：国家自然科学基金项目资助(51322502)

收稿日期：2015-04-09修改稿收到日期：2015-06-02

通信作者王刚 男，教授，博士生导师，1975年11月生

中图分类号:TH113；O48

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.006

第一作者 陈良 男，硕士,助教，1989年10月生

E-mail: zaehwang@hotmail.com