大型液体火箭结构纵横扭振动与推进系统耦合(POGO)稳定性分析

王庆伟， 谭述君， 吴志刚,， 杨云飞， 于子文

(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室，辽宁 大连　116023；2.大连理工大学 航空航天学院，辽宁 大连　116023；3.北京宇航系统工程研究所，北京　100076)

大型液体火箭结构纵横扭振动与推进系统耦合(POGO)稳定性分析

王庆伟1， 谭述君2， 吴志刚1,2， 杨云飞3， 于子文3

(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室，辽宁 大连116023；2.大连理工大学 航空航天学院，辽宁 大连116023；3.北京宇航系统工程研究所，北京100076)

摘要：大型液体火箭结构振动模态空间分布的特征，导致结构横向和扭转振动对传统POGO回路稳定性产生影响。对此，基于改进的Rubin建模方法，建立了结构纵横扭振动与推进系统液路脉动耦合的POGO回路模型。该模型具有非奇异的优点，可以直接应用于频域分析和时域仿真。基于该模型分析了中国某型号液体火箭推进系统的泵增益和蓄压器能量值等重要参数对结构纵向振动以及横向和扭转振动稳定性的影响。研究得出，泵增益的增大不仅使结构纵向第2、4阶模态不稳定也使结构横向第2阶不稳定。通过调节蓄压器能量值，不但可使结构纵向失稳的模态由不稳定变为稳定，也使结构横向失稳的模态由不稳定变为稳定，说明该型号液体火箭的推进系统不仅与结构系统的纵向模态存在耦合作用，也与横向模态存在耦合作用。因此，对于大型液体捆绑火箭，在研究POGO稳定性时分析结构纵横扭振动与推进系统的耦合作用是有必要的。

关键词：POGO；纵横扭模态；稳定性；耦合模型

POGO振动是液体运载火箭在飞行中由于推进系统中的压力和流量脉动与结构系统弹性振动之间的耦合作用产生的一种不稳定振动。其典型的表现形式为整箭突然自发产生纵向周期振动，振动逐渐增至某一最大值后又逐渐减小，直至振动消失。POGO振动产生的加速度会对箭上的仪器、设备以及航天员造成不利影响，振动严重时可能导致飞行任务失败。因此，自1960-1962年首次在Thor/Agena 和TitanII火箭上发现POGO振动以来，得到了学者们的广泛研究[1-6]。

传统的POGO稳定性分析，将火箭结构动力学简化为一维梁附加质量块模型，主要考虑结构纵向模态与推进系统的耦合。Rubin[1]采用单推进剂-单发动机模型研究了POGO产生的机理，提出了分析POGO振动稳定性的临界阻尼比法。Zhao等[5]则在参数空间分析了推进系统与结构系统的频率比等参数对POGO振动稳定性的影响。Dotson等[6]指出了POGO问题是任务依赖性的(“mission specific”)。徐得元等[7]利用有理多项式逼近提出了POGO系统振动特性的一种快速求解方法。唐冶等[8]对液体火箭推进系统频率特性进行了灵敏度分析。Oppenheim等[9]利用有限元法，建立了一种分析POGO振动稳定性的先进方法，该方法通过将推进系统划分为八种基本物理单元，以推进系统节点上的脉动压强、脉动重量位移和结构模态位移为变量，建立了POGO振动分析模型。该模型可通过程序自动生成，具有很强的通用性，已经成功地用于Atlas-Ⅱ/Centaur和CZ-2FPOGO问题研究中。但是由于模型中存在大量的代数方程，导致模型矩阵奇异，增加计算量的同时，不便于时域仿真。Wang等[10]在文献[9]模型基础之上，基于独立单元的概念，提出了“改进的Rubin模型”，建立了全微分形式的POGO振动模型，与文献[9]中的模型相比，维数降低近一半，大大降低了计算量，且该模型为非奇异模型，可直接用于时域仿真分析。

传统的POGO模型和分析忽略了箭体横向振动和扭转振动与推进系统之间的耦合，然而，随着现代液体火箭规模的增大，特别是捆绑火箭的出现，箭体的结构动力学特性变得复杂，一方面，箭体的模态出现低频的密集模态，另一方面，大量的模态呈空间分布，在纵横扭方向上均存在明显的投影[11-13]，结构的横向和扭转模态也有可能与推进系统耦合而引起横向振动或扭转振动的不稳定。如土星V[14]的一次飞行记录显示，火箭飞行中出现了两个耦合，一个是纵向振动与推进系统耦合产生POGO振动，产生一个幅值为0.72 g的加速度；另一个为结构纵向与横向振动的耦合，在登月舱处产生一个频率为5.3 Hz、幅值为0.65 g的振动加速度，达到了破坏极限。肖丽红[15]指出，我国某运载火箭姿控回路的速率陀螺在整个助推段出现高频抖动，而产生抖动的原因是由于助推器的模态、纵向振动与扭转振动之间存在耦合。王建民等[12, 16]利用试验和计算相结合的方法，得到了捆绑火箭全箭的动力学特性，提出了基于空间模态进行POGO设计的思想，特别是包含纵向分量的空间模态，如横向第2阶模态。赵治华[17]利用多体系统动力学方法，分析了包含结构纵横扭的液体火箭POGO振动稳定性。荣克林等[4]通过全箭模态计算，管路模态试验等方法研究了多模态多推力影响下的POGO振动稳定性。杨云飞等[11]在建立液体捆绑火箭的姿态动力学模型时充分考虑了结构弹性振动与姿态动力学的耦合，其中横向振动模态对火箭的姿态稳定至关重要，因此推进系统与结构纵横扭模态的耦合对姿控系统的稳定是一个潜在的威胁。所以对于大型液体捆绑火箭，在分析POGO振动稳定性时，综合考虑结构纵向、横向和扭转模态与推进系统的耦合作用是很有必要的。

本文将“改进的Rubin模型”[10]扩展到空间结构模态中，建立了结构纵横扭振动与推进系统耦合的POGO回路非奇异模型，通过推进系统参数泵增益和蓄压器能量值，分析了我国某型号液体火箭推进系统与结构纵横扭振动的耦合稳定性。

1POGO回路模型

文献[10]提出了基于独立单元建模的思想，通过划分和组合将推进系统划分为九类独立单元。将推进系统节点上脉动压强(推力室除外)作为连接条件而不是变量，使得“改进的Rubin模型”全部由微分方程组成。所以“改进的Rubin模型”为非奇异模型，可直接用于频域分析和时域仿真，而且维数与Rubin模型[9]相比降低一半左右，提高了计算效率。将“改进的Rubin模型”扩展到结构的空间模态中，从而建立结构纵横扭模态与推进系统耦合的POGO回路模型，这种扩展主要体现在两个方面。一方面为结构系统对推进系统的影响，即结构纵向振动、横向振动对推进系统中流体的脉动压强和重量位移产生作用。另一方面为结构系统的变化，即结构系统的方程由纵横扭模态振动方程组成。推进系统中流体单元由于脉动压强和重量位移产生的干扰力影响结构的纵横扭模态振动。

1.1推进系统模型

w=[w1,w2,w3,…,wNp]T

(1)

ptc=[ptco1,ptcf1,…,ptcoNth,ptcfNth]T

(2)

得出推进系统的动力学方程为[10]

(3)

(4)

(5)

式中，wi为第i节点上的相对重量位移，与物理位移ui的关系为wi=ρAigui，其中，ρ和g分别为流体密度和重力加速度，Ai为i结点的截面积。ptcoj和ptcfj分别为推力室中第j节点上氧化剂和燃料喷嘴出口产生的脉动压强。Mp，Rp，Kp，S，L和H为推进系统的系数矩阵。fps为结构系统的弹性振动对推进系统产生的作用力向量。将“改进的Rubin模型”扩展到结构空间模态中，对推进系统模型的影响即体现在fps的描述式5)中，

rp=[rp1,rp2,rp3,…,rNp]T

(6)

式中，rpi为第i个推进系统中节点的弹性振动空间位移向量，包含了结构的纵向和横向弹性振动。rp与整箭结构系统节点的位移向量r的关系可表示为rp=Xpsr，其中Xps为常数转换矩阵。在空间模态中可将弹性振动位移表示为

rp=XpsΦq

(7)

其中，Φ为箭体结构的空间模态矩阵，包含结构纵向、横向和扭转模态。q为模态坐标向量。将式(7)代入式(5)，fps可表示为

(8)

其中，Φps=XpsΦ，Φps可看作为推进系统节点处的模态矩阵。

1.2结构系统模型

对“改进的Rubin模型”的另一个扩展即建立基于全箭动特性的纵向、横向和扭转模态的结构系统方程。其中推进系统单元对结构系统产生的空间力向量直接作用于结构纵横扭振动方程中。全箭三维模态能更好反映捆绑火箭的动力学特性，是液体捆绑火箭POGO设计和姿控系统稳定设计的基础，特别是助推器对整箭特性的影响[12]。将结构的方程在空间模态下分解，得到结构的方程形式为

(9)

fsp=Xspfp=

(10)

ΦTfsp=

(11)

1.3POGO振动模型

综合式(1)～式(11)，选取耦合系统的状态变量v为

(12)

POGO振动系统的耦合动力学方程可写为

(13)

其中，

式(13)即结构纵横扭振动与推进系统耦合的POGO振动分析模型。可用于分析结构纵向振动和横向振动对推进系统中管路流体的影响以及推进系统单元产生的干扰力对结构纵横扭振动的影响。由于Mp和Ms为非奇异阵，因此E矩阵为可逆矩阵。因此，式(13)可以描述为

(14)

其中，

(15)

由于E矩阵的分块对角特性，根据分块对角阵的求逆引理，

(16)

其中

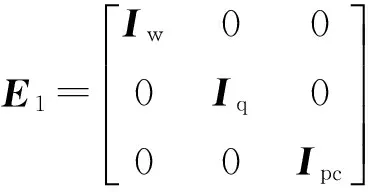
(17)

(18)

(19)

其中，

2结构纵横扭振动与推进系统耦合稳定性分析

如引言所述，捆绑火箭模态空间分布，导致了推进系统与结构纵横扭模态均存在耦合作用，在POGO分析中要充分考虑结构纵横扭振动与推进系统的耦合作用[12]。本节基于式(13)或式(14)所示的模型，以我国某型号液体捆绑液体火箭为例，通过频域分析和时域仿真分析了推进系统中重要参数——泵增益和蓄压器能量值对某型号运载火箭150 s时刻的模型POGO回路稳定性的影响。泵增益和蓄压器能量值均通过与设计值作商进行无量纲处理，其中泵增益的变化范围根据工程经验设定为设计值的1倍～3倍，蓄压器能量值的变化范围设定为设计值的0倍～1.8倍。结构取横向前2阶，纵向前5阶，扭转前3阶。芯级推进系统的模型以及单元划分示意图如图1所示。

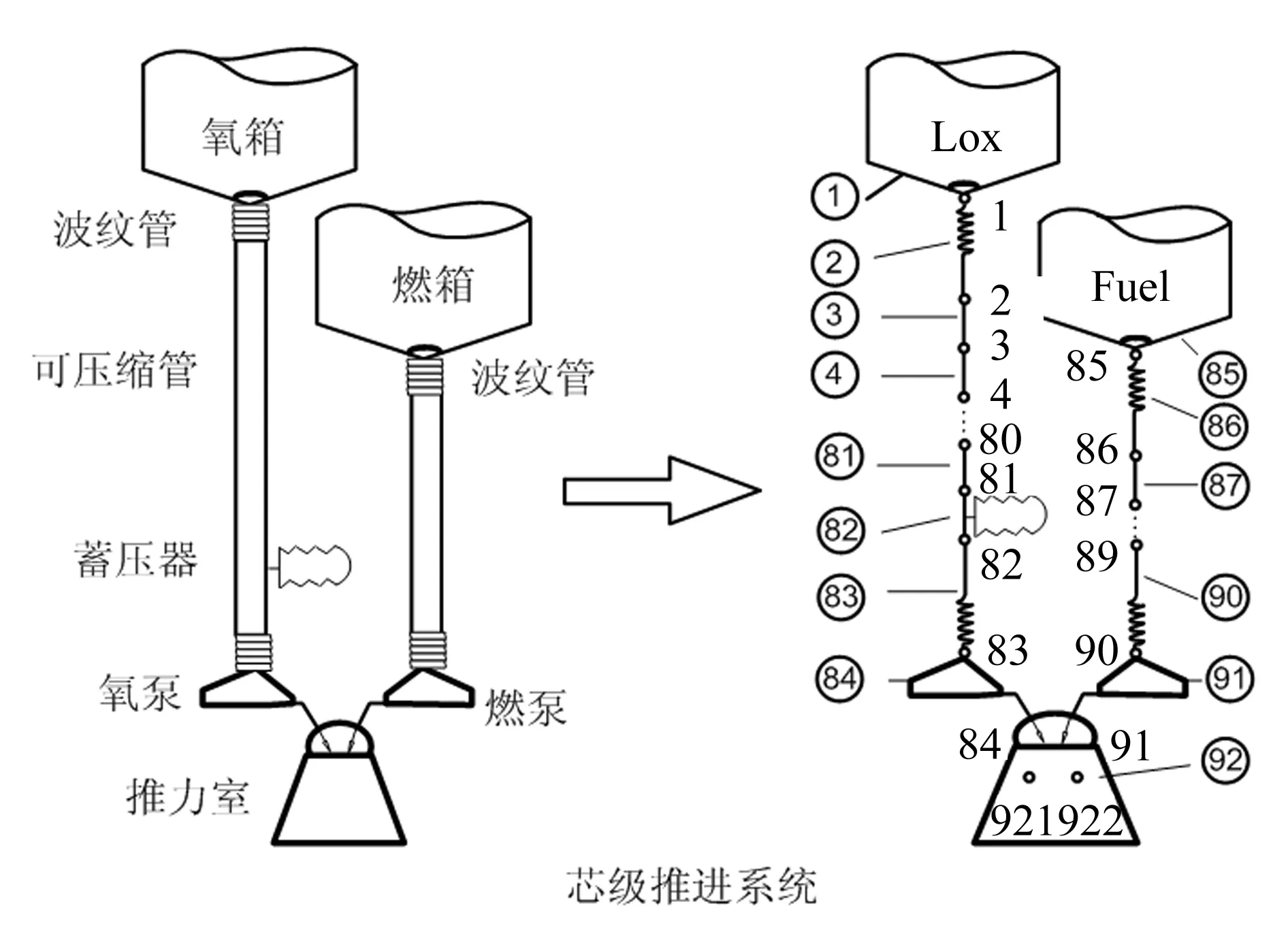
图1　推进系统示意图及划分节点示意图Fig.1 Schematic diagram of propulsion system and elements division

在频域分析中，通过分析系统的模态阻尼比ξ来判断系统的稳定性。

按照图1所示的节点划分示意图，通过程序自动生成式(13)中的各系数矩阵。求该模型的特征值，可以得到一组复数形式的特征值向量s，可以描述为

s=σ±iλ

(20)

其中，σ和λ分别为特征值向量的实部和虚部，i为虚数单位。每一阶特征值sj，均可以重新描述为系统的模态阻尼比ξ和频率ω的形式，即

sj=-ξω±i(1-ξ2)1/2ω

(21)

其中

(22)

当结构的模态阻尼比小于零(即系统的特征值的实部大于零)时，此时系统是不稳定的。反之，系统是稳定的。当模态阻尼比等于零，系统临界稳定。

在时域仿真中，本文基于式(1)～式(11)在Matlab中建立仿真POGO振动的simulink模型，如图2所示，以进一步与频域分析结果对应。通过仿真曲线可以直观的观察系统发散的程度。在仿真过程中，为了仿真结果的可比性，每次仿真对应的初始条件完全相同，且采用完全相同的推力室脉动压强干扰，系统某一阶模态振动可以表示为

v(t)=e-ξωtRe{v(sj)ei(1-ξ2)1/2ωt}

(23)

其中，Re表示解的实部。由式(23)可以看出当系统不稳定时，负的模态阻尼比不断吸收能量导致系统的振动逐渐发散，而当系统稳定时，正的模态阻尼比会通过能量耗散使系统保持稳定。

图2　Simulink仿真示意图Fig.2 Schematic diagram of simulink model

2.1泵增益的影响

图3给出了泵增益逐渐增大时结构横向1～2阶、纵向1～5阶和扭转1～3阶模态阻尼比的变化。其中结构的模态阻尼比初始值为0.5%。

图3(a)显示，随着泵增益的增大，横向第1阶、纵向第1阶以及扭转第1～3阶的模态阻尼比变化很小，纵向第4、5阶的模态阻尼比略有增大，纵向第3阶阻尼比单调减小，说明泵增益的增大导致纵向第3阶模态稳定性大幅度下降，纵向第4阶模态和第5阶模态的稳定性略有增强，对扭转第1～3阶、横向第1阶和纵向第1阶模态的稳定性影响很小。图3(b)显示，随着泵增益的增大，结构的横向第2阶和纵向第2阶的模态阻尼比单调减小，由大于零变为小于零，即由稳定变为不稳定，说明泵增益的增大导致了横向第2阶和纵向第2阶模态失稳。

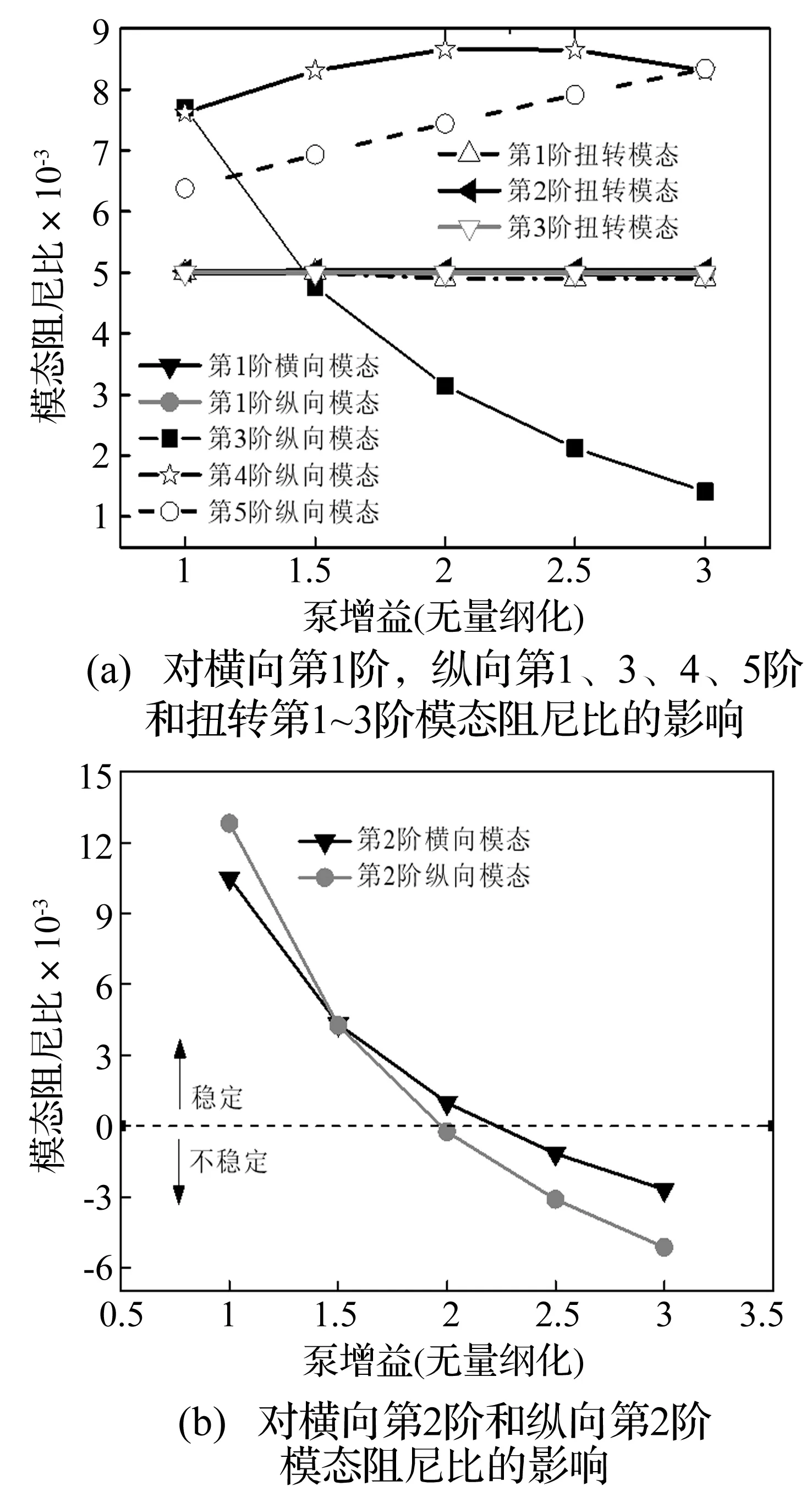
图3　150 s泵增益对结构系统稳定性影响Fig.3 Effect of pump gain to the modal damping ratio of structural system at 150th second

图4和图5分别给出了泵增益增大为设计值的1.5倍和3倍时纵向第2阶和横向第2阶模态加速度仿真曲线。图4显示，当泵增益增大为设计值的1.5倍时，在150 s附近横向第2阶模态和纵向第2阶模态振动加速度均保持稳定状态，图5显示当泵增益增大为设计值的3倍时，横向第2阶模态和纵向第2阶模态的振动加速度均在150秒附近发散。图4和图5中的仿真结果说明在完全相同的初始条件以及干扰条件下，泵增益增大为设计值的1.5倍时，第2阶纵向和横向的模态加速度均保持稳定，但泵增益增大为设计值的3倍时，第2阶纵向和横向模态加速度均发散，这与图3中的频域分析结果一致。

图4　泵增益增大为设计值1.5倍时仿真曲线Fig.4 Simulation curve with pump gain increased to 1.5 times of designing value

图5　泵增益增大3倍时仿真曲线Fig.5 Simulation curve with pump gain increased to 3 times of designing value

2.2蓄压器能量值的影响

在POGO设计时，通常在氧路或燃路的泵前安装蓄压器来抑制POGO振动发散。蓄压器能量值是蓄压器中可调节的重要参数。图6给出了在泵增益增大为设计值的3倍的基础上，蓄压器能量值在设计值的0倍～1.8倍内变化时结构纵横扭模态稳定性的变化。

由图6(a)可知，由于结构与推进系统的耦合作用，纵向第3阶的模态阻尼低于0.5%，说明耦合作用大大降低了纵向第3阶的稳定性，而第5阶纵向模态阻尼比均大于0.5%，说明耦合作用提高了纵向第5阶的稳定性。随着蓄压器能量值增大，结构第3阶纵向模态阻尼比先减小后增大，第5阶纵向结构模态阻尼比先增大后减小，扭转前3阶模态以及横向1阶纵向1阶模态阻尼比变化很小。图6(b)显示随着蓄压器能量值的增大，横向第2阶和纵向第2阶的阻尼比先减小后增大，当蓄压器能量值增大为初始值的1.5倍时，横向第2阶模态和纵向第2阶模态阻尼比均大于零，表明此时横向第2阶模态和纵向第2阶模态由不稳定变为稳定。当蓄压器能量值大于零时纵向4阶模态阻尼比由负变正，即纵向第4阶模态由不稳定变为稳定。

图6　150 s蓄压器能量值对结构系统稳定性影响Fig.6 Effect of accumulator energy value to the modal damping ratio of structural system at 150th second

比较图6(b)和图3(b)可以得出，泵增益的增大导致结构横向第2阶和纵向第2阶，第4阶模态失稳，通过增大蓄压器能量值，可以增大失稳模态的阻尼比直至稳定，而且蓄压器能量值对这些模态阻尼比的影响是非线性的。

2.1与2.2节的数值算例表明，结构纵向第2阶、第4阶、第5阶模态和横向第2阶模态与推进系统的耦合作用较大，且与泵增益和蓄压器能量值的关系是非线性的。泵增益的增大会导致横向2阶模态与纵向第2阶、4阶模态失稳。增大蓄压器能量值，能够使横向2阶模态与纵向第2阶、第4阶模态由不稳定变为稳定。泵增益和蓄压器能量值对扭转模态稳定性影响较小，说明对于该型号的火箭，扭转模态与推进系统的耦合作用相对结构纵向和横向模态较小，箭体的横向模态与纵向模态均与推进系统存在较强的耦合作用。

在分析POGO稳定性时，对于纵横扭模态耦合作用明显的大型液体捆绑火箭，特别是重型运载火箭，综合考虑结构纵向、横向和扭转模态和与推进系统的耦合作用是非常有必要的。

3结论

本文将“改进的Rubin模型”扩展到结构纵横扭模态空间，建立了结构纵横扭振动与推进系统耦合的POGO振动模型。基于该模型，通过时域仿真和频域分析，研究了我国某型号运载火箭纵横扭模态与推进系统的耦合稳定性。研究得出：

(1) 推进系统与结构纵横扭振动存在耦合作用。如算例中泵增益的增大，导致了结构纵向第2阶、第4阶和横向第2阶模态失稳。降低了纵向第3阶的稳定性。通过调节蓄压器能量值，可以使失稳的结构模态恢复稳定。对于纵横扭模态耦合作用明显的大型液体捆绑火箭，在POGO回路设计时，必须要充分考虑结构纵横扭振动与推进系统的耦合稳定性。

(2) 结构横向振动稳定对姿控系统的稳定性至关重要，因此基于结构纵横扭振动与推进系统耦合的POGO回路模型，可进一步研究推进系统与姿控系统的耦合作用，研究推进系统对姿控系统稳定性的影响。

参 考 文 献

[1] Rubin S. Longitudinal instability of liquid rockets due to propulsion feedback[J]. Journal of Spacecraft and Rockets, 1966, 3(8):1188-1195.

[2] 王其政，张建华，马道远. 捆绑液体火箭跷振(POGO)稳定性分析[J]. 强度与环境，2006, 33(2): 6-11.

WANG Qi-zheng, ZHANG Jian-hua, MA Dao-yuan. POGO analysis of cluster liquid rocket[J]. Structure Environment Engineering, 2006,33(2): 6-11.

[3] 马道远,王其政,荣克林. 液体捆绑火箭POGO稳定性分析的闭环传递函数法[J]. 强度与环境，2010, 37(1): 1-7.MA Dao-yuan, WANG Qi-zheng, RONG Ke-lin. Close-looptransfer function of POGO stability analysis for binding liquid-propellant rocket[J]. Structure Environment Engineering, 2010, 37(1):1-7.

[4] 荣克林，张建华，马道远，等. CZ-2F火箭POGO问题研究[J]. 载人航天，2011(4): 8-18.

RONG Ke-lin, ZHANG Jian-hua, MA Dao-yuan, et al. Research on POGO problem for CZ-2F rocket[J]. Manned Spaceflight, 2011(4): 8-18.

[5] Zhao Z H, Ren G X, Yu Z W, et al. Parameter Study on POGO stability of liquid rockets[J]. Journal of Spacecraft and Rockets, 2011, 48(3): 537-541.

[6] Dotson K W, Rubin S, Sako B H. Mission-specific POGO stability analysis with correlated pump parameters[J]. Journal of Propulsion and Power, 2005, 21(4): 619-626.

[7] 徐得元，郝雨，杨琼梁，等. 液体火箭纵向耦合振动特性的快速求解方法[J]. 宇航学报，2014, 35(1): 21-27.

XU De-yuan, HAO Yu, YANG Qiong-liang, et al. Fast matrix algorithm for POGO instability prediction in liquid rocket[J]. Journal of Astronautics, 2014,35(1): 21-27.

[8] 唐冶，方勃，李明明，等. 液体火箭推进系统频率特性的灵敏度分析[J]. 宇航学报，2014, 35(8): 878-883.

TANG Ye, FANG bo, LI Ming-ming, et al. Sensitivity analysis of frequency characteristic for propulsion system in liquid rocket[J]. Journal of Astronautics, 2014,35(8):878-883.

[9] Oppenheim B W, Rubin S. Advanced POGO stability analysis for liquid rockets[J]. Journal of Spacecraft and Rockets, 1993, 30(3): 360-373.

[10] Wang Q W, Tan S J, Wu Z G, et al. Improved modelling method of POGO analysis and simulation for liquid rockets[J]. Acta Astronautica, 2015, 107: 262-273.

[11] 杨云飞，李家文，陈宇，等. 大型捆绑火箭姿态动力学模型研究[J]. 中国科学E辑:技术科学，2009, 39(3): 490-499.

YANG Yun-fei, LI Jia-wen, CHEN Yu, et al.Study on attitude dynamics modeling for largre boundled rockets[J]. Science in China Series E: Technical Science, 2009,39(3):490-499.

[12] 王建民，荣克林，冯颖川，等. 捆绑火箭全箭动力学特性研究[J]. 宇航学报，2009, 30(3): 821-826.

WANG Jian-min, RONG Ke-lin, FENG Ying-chuan, et al. The research of dynamic characteristics for the strap-on launch vehicle[J]. Journal of Astronautics, 2009, 30(3): 821-826.

[13] 杨云飞，李东，谭述君，等. 运载火箭纵横扭大回路耦合动力学研究[J]. 中国科学E辑:技术科学，2014, 44(5): 510-516.

YANG Yun-fei, LI Dong, TAN Shu-jun, et al. A study of longitudinal-lateral-torsional coupling dynamics of launch vehicles[J]. Science in China Series E: Technical Science, 2014,44(5):510-516.

[14] Rtan R S, Papadopoulos J G, Kiefling L A, et al. A study of Saturn As-502 coupling longitidinal structural vibration and lateral bending respnse during boost[J]. Journal of Spacecraft and Rockets, 1970, 7(2): 113-118.

[15] 肖利红. 捆绑火箭助推段扭转与纵向振动耦合分析[J]. 航天控制, 2001(2):14-19.

XIAO Li-hong.Coupling analysis of tortional and longitudinal vibration of bundled rocket during boost[J]. Aerospace Control, 2001(2): 14-19.

[16] 王建民，吴艳红，张忠，等. 运载火箭全箭动特性三维建模技术[J]. 中国科学E辑:技术科学，2014, 44(1): 50-61.

WANG Jian-min, WU Yan-hong, ZHANG Zhong, et al. Three-dimensional modeling technology for dynamic characteristics of the launch vehicle[J]. Science in China Series E: Technology Science,2014,44(1): 51-61.

[17] 赵治华. 液体火箭POGO振动的多体动力学建模及稳定性分析[D]: 北京：清华大学, 2011.

POGO stability analysis of large liquid rocket considering longitudinal, lateral and torsional vibration modes of structural system

WANG Qing-wei1, TAN Shu-jun2, WU Zhi-gang1,2, YANG Yun-fei3, YU Zi-wen3

(1. State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian 116023, China; 2. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116023, China;3. Beijing Aerospace System Engineering Institute, Beijing 100076, China)

Abstract:The lateral and torsional vibration of structural system has importance influence on the stability of traditional POGO of large liquid rocket because of the spatial distribution characteristics of structural modes. A model for POGO stability analysis considering longitudinal, lateral and torsional modals of structural system was developed based on the improved Rubin’s modeling method. Because of its non-singularity, the model can be directly used for frequency-domain analysis and time-domain simulation. The effects of pump gain and energy value of the accumulator on the POGO stability of a certain type of China liquid rocket were studied. The results show that the second order lateral modal, the fourth order lateral modal and the second order longitudinal modal may enter into unstable regions with the increase of pump gain. By adjusting the energy value of the accumulator, both the unstable longitudinal modal and lateral modal may become stable, which indicates that the coupling effect exists between the propulsion system and the longitudinal and lateral modals of the structural system in this rocket. Therefore, it is necessary to take the longitudinal, lateral and torsional modals of structural system into consideration in the POGO analysis of large liquid rockets.

Key words:POGO; longitudinal; lateral and torsional modal; stability; coupling model

基金项目：国家自然科学基金资助项目(11072044;11372056)；高等学校博士点基金资助项目(20110041130001)

收稿日期：2015-04-08修改稿收到日期：2015-05-18

通信作者谭述君 男，博士，讲师，1979年8月生

中图分类号:O32,V47

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.027

第一作者 王庆伟 男，博士生，1988年3月生