变转速及齿轮噪源干扰下基于IDMM与EMD的滚动轴承故障诊断方法

赵德尊， 李建勇， 程卫东

(北京交通大学 机械与电子控制工程学院，北京　100044)

变转速及齿轮噪源干扰下基于IDMM与EMD的滚动轴承故障诊断方法

赵德尊， 李建勇， 程卫东

(北京交通大学 机械与电子控制工程学院，北京100044)

摘要：旋转设备中变转速工作模式和齿轮噪源是影响滚动轴承故障诊断的关键性难题，现有的方法虽然取得一定进展，但是对辅助设备的依赖以及方法步骤繁琐等问题依然突出，因此提出了基于峰值啮合倍频(Instantaneous Dominant Meshing Multiply,IDMM)和经验模式分解(Empirical Mode Decomposition,EMD)的滚动轴承故障诊断方法。该方法首先采用峰值搜索算法从混合信号的时频图中提取齿轮啮合倍频趋势线，将该趋势线等效为轴承转频对混合信号进行等角度重采样；其次对重采样信号进行EMD分解得到本征模态函数(Intrinsic Mode Function,IMF)之和，计算各IMF分量与重采样信号的互相关系数后根据预设的互相关系数阈值选取合适的IMF分量；最后对选取的IMF分量进行包络谱分析，进而判断轴承是否发生故障。仿真和实测信号分析证明该方法在无转速测量装置的情况下能有效去除齿轮噪声对滚动轴承故障诊断的影响。

关键词：变转速；齿轮噪源；滚动轴承故障诊断；IDMM；EMD

变转速工作模式和齿轮噪源干扰是阻碍滚动轴承故障诊断的两大难题[1]。转速变化将直接影响滚动轴承振动信号的频率和幅值。在频率方面，由轴承故障引起的冲击将不再以等时间间隔出现，导致现有的以高频共振技术为代表以转速平稳为前提的滚动轴承故障诊断方法失效。在时域上，滚动轴承振动信号的幅值也将随着转速变化而发生改变。旋转设备中齿轮啮合引起的噪声具有幅值上的优势，即使是在齿轮健康滚动轴承有明显故障的情况下，齿轮噪声也会掩盖故障轴承引起的冲击特征。另外，齿轮噪源也会影响由滚动轴承引起的共振频带的获取。

针对上述单一因素的影响许多学者做出了探索。阶比跟踪技术[2-3]是处理变转速工作模式的有效方法，其思想是获得相对于参考轴的恒定角增量采样，将时域的非周期信号转化为角域周期信号以消除转速变化对振动信号的影响。常用的阶比跟踪方法有硬件阶比跟踪法、计算阶比跟踪法[4]、以及基于瞬时频率估计的阶比跟踪法[5-6]等。其中，基于瞬时频率估计的阶比跟踪算法因克服了硬件安装空间及安装成本对计算阶比跟踪以及硬件阶比跟踪的限制近年来得到学者的广泛关注，其核心是从原始振动信号中提取等效转频进而进行角域重采样。然而对于齿轮和故障轴承混合信号而言，由于高幅值齿轮噪源的干扰，难以从混合信号中提取到滚动轴承的转频信息。传统的消除齿轮噪源干扰的方法主要包括：时域同步平均技术(Time Synchronous Average,TSA)、线性预测算法(Linear Prediction)、自适应噪声消除算法(Adaptive Noise Cancellation,ANC)、单一自适应噪声消除算法(Self-adaptive Noise Cancellation,SANC)离散/随机分离算法(Discrete/Random Separation,DRS)以及编辑倒谱算法(Edited Cepstrum)等[7-8]。上述算法中除ANC算法外，都要求相应的转频不能有太大的波动，而ANC算法需要依靠辅助设备获取齿轮的参考信号以及对辅助设备的安装位置要求较高。

为实现两种影响因素并存状态下的滚动轴承的故障诊断，Borghesani等[9]采用阶比跟踪技术消除转速变化对混合信号的影响，再利用传统齿轮去噪算法在角域实现齿轮噪源的去除，最后将去噪后的信号反采样回时域，根据轴承转速信息重采样以实现故障诊断。Borghesani提出的方法虽然在一定程度上解决了变转速及齿轮噪源干扰条件下的滚动轴承的故障诊断这一问题，但是该方法需要辅助设备测取转速信息，对于受安装空间及安装成本限制的机械设备无能为力，另外齿轮角域重采样-齿轮噪源去除-时域逆采样-轴承信号角域重采样等一系列算法会消弱本来就相对微弱的轴承信号中的故障冲击成分。王天杨等[10]则直接从混合信号中提取IDMM趋势线，以此构造ANC算法所要求的参考信号，去除齿轮噪声后根据剩余信号估计瞬时转频，重采样得到角域平稳信号，进而包络分析得到包络谱对轴承进行故障诊断。王天杨提出的ANC改进算法虽然摆脱了滚动轴承故障诊断过程对辅助设备的依赖，但是ANC算法中自适应滤波参数的确定需要根据后续的包络谱不断尝试以得到最优值，选择不当会直接影响去噪效果，过程较为繁琐，即使选出最优滤波参数，ANC算法也只能消除齿轮峰值啮合倍频，对于其他阶的齿轮啮合频率无能为力。另外根据去噪后的信号提取的等效转频存在较大误差，对滚动轴承故障诊断有一定影响。

为进一步改进现有的变转速及齿轮噪源干扰条件下的滚动轴承的故障诊断方法，本文引入EMD算法，结合齿轮啮合倍频趋势线这一概念实现变转速及齿轮噪源干扰条件下的滚动轴承的故障诊断。本文方法摆脱了诊断过程对辅助设备的依赖，避免了参数选取过程中的复杂计算以及多次重采样对轴承信号的消弱，成功的分离出了齿轮啮合频率及其倍频。

1IDMM趋势线及EMD算法

1.1IDMM趋势线

匀转速条件下的齿轮振动信号为窄带周期信号，该特性使其振动信号在频谱相应的啮合频率以及倍频处出现明显峰值。其中幅值最大的突出峰值对应的横坐标与齿轮转频之间存在固定的比例关系，公式如

(1)

当齿轮转速发生变化时，最大啮合倍频也会以相同的变化趋势发生改变。文献[10]将最大啮合倍频定义为峰值啮合倍频，即IDMM。IDMM随时间变化所构成的趋势线为IDMM趋势线。滚动轴承与齿轮的混合信号中，齿轮信号的振幅远大于轴承信号的幅值，所以IDMM趋势线容易从混合信号的时频图中直接提取。本文利用短时傅里叶变换(Short-time Fourier Transform，STFT)求取混合信号的时频表达：

(2)

式中，x(τ)为滚动轴承与齿轮的混合信号；g(τ)为高斯窗函数。

利用峰值搜索算法求取IDMM。峰值搜索算法的原理是从时频图上搜索每一时刻对应的最大幅值点，该幅值点所对应的频率值即为该时刻的瞬时啮合倍频。利用峰值搜索算法求取IDMM的具体公式如下：

IDMMi=argmax{IFTi}(i=1,2,…,n)

(3)

式中，IFT代表瞬时频谱；i为瞬时频谱对应的序号,取值是1～n；arg max函数表示IFTi取得最大值时对应的频域横坐标，瞬时频谱的总数n将由原始信号与窗函数的长度决定，IDMM趋势线为瞬时峰值啮合倍频的集合。

1.2EMD算法

EMD方法是由Huang[11]提出的一种自适应的信号分解方法。它基于信号的局部特征，将原始信号分解为许多的窄带分量，即本征模态函数(Intrinic Mode Function,IMF)。IMF必须满足下面两个条件：① 在整个数据段内,极值点的个数和过零点的个数必须相等或最多相差一个；② 在任意时刻,由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零。

EMD分解的实现过程如下：

步骤1确定信号x(t)的所有局部极值点，然后用三次样条插值分别将所有的局部极大值点和局部极小值点连接起来，形成上包络线和下包络线,包络线包括了所有的信号数据。

步骤2计算上、下包络线的平均值，记为m1，求出

h1=x(t)-m1

(4)

如果h1是一个IMF,那么它就是信号x(t)的第一个IMF。

步骤3如果h1不是一个IMF，则将h1作为原始数据，重复步骤1～2得到上、下包络线的平均值，记为m11，计算h11=h1-m11，并判断是否满足IMF的条件，如果不满足，则重复循环，计算h1k=h1{k-1}-m1k，直到h1k是一个IMF。记c1=h1k，则c1为信号x(t)的第一个IMF。

步骤4将c1从x(t)中分离出来，得到:

r1=x(t)-c1

(5)

将r1作为原始数据，重复步骤1～3，得到第二个IMF。重复循环n次,到信号x(t)的n个IMF，于是有:

r2=r1-c2…rn=rn-1-cn

(6)

当rn成为一个单调函数不能再从中提取满足IMF条件的分量时，循环结束。经EMD分解，信号表示为：

(7)

式中，rn称为残余函数,代表信号的平均趋势。

2基于IDMM与EMD的滚动轴承故障诊断方法

变转速及齿轮噪源干扰条件下的滚动轴承振动信号的时频图中，齿轮某一阶的啮合倍频具有明显的幅值优势，利用峰值搜索算法即可提取。由于该啮合倍频与齿轮转频以及轴承转频有固定比例关系，因此IDMM趋势线可以等效为轴承转频对原始混合信号进行角域重采样，将时域非平稳信号转变成角域平稳信号。EMD算法基于信号自身的特征进行分解，不需要信号的先验知识以及预定基函数，具有很好的适应性。另外，EMD分解得到的IMF分量根据频率从到高低依次分布，而轴承信号为高频共振信号，齿轮啮合干扰信号一般分布在低频，所以EMD算法可以将混合信号中的齿轮干扰成分剔除。本文根据多次试验的分析结果，按照确保含有滚动轴承故障信息的IMF分量不被剔除，以及尽可能减少选取的IMF数量这两条原则，设定互相关系数阈值θ=0.5，选取互相关系数大于0.5的IMF分量进行包络谱分析。互相关系数的计算公式如式(8)所示：

(8)

式中：E(x)为x的数学期望，μx和μy分别为原始信号x和y的均值，σx和σy分别为原始信号x和y的标准差。

本文方法的流程图如图1所示，主要步骤如下：① 利用峰值搜索算法从原始信号的时频图中提取IDMM趋势线；② 以IDMM趋势线为轴承等效转频对原始信号进行等角度重采样，得到角域重采样信号；③ 利用EMD算法对重采样信号进行分解，得到IMF分量；④ 利用式(8)求取各IMF分量与角域重采样信号的互相关系数，根据预设的相关系数阈值选取合适的IMF分量；⑤ 对选取的IMF分量进行包络谱分析，根据包络谱对滚动轴承进行诊断。

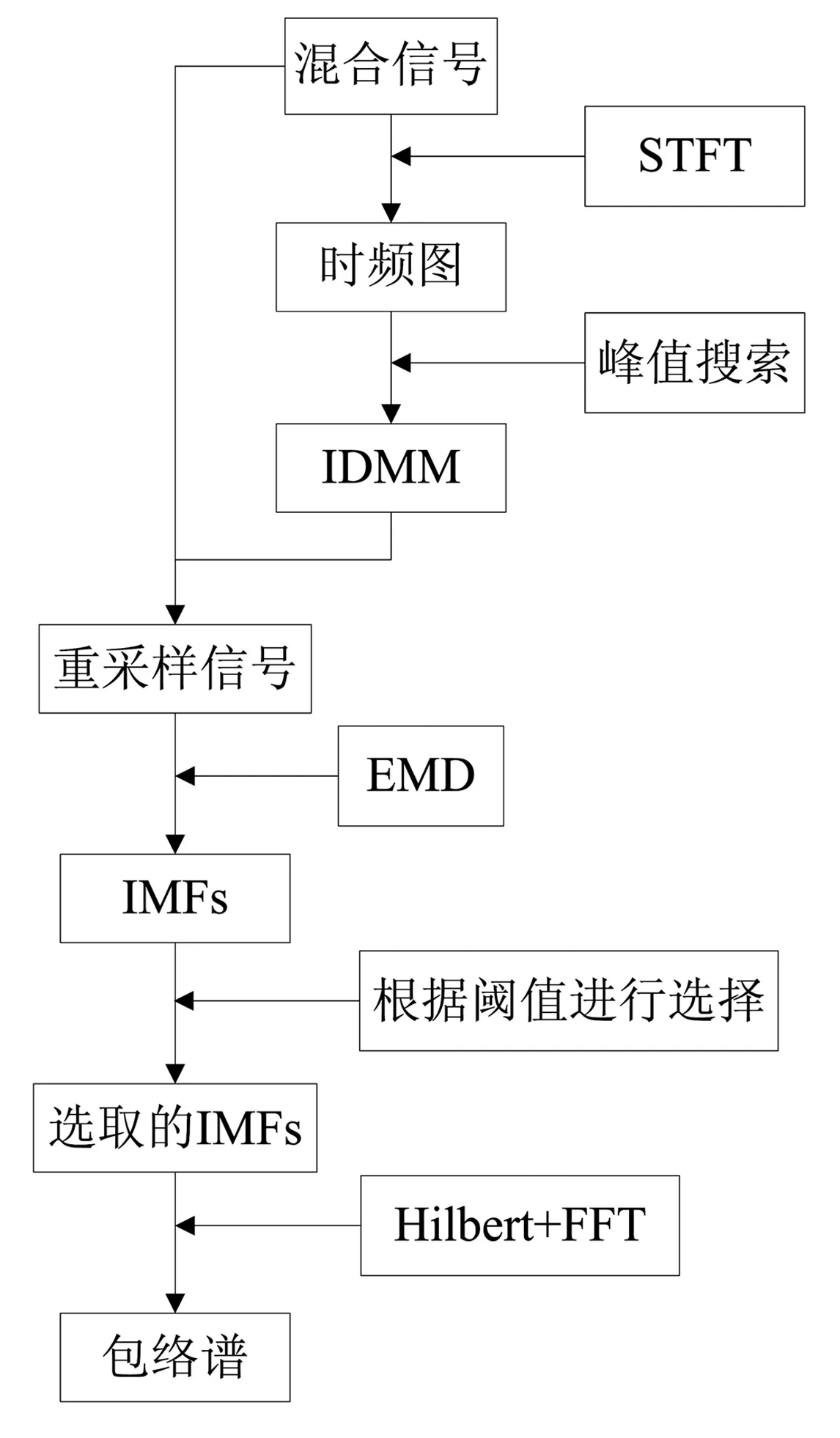
图1　基于IDMM和EMD的滚动轴承故障诊断方法的流程图Fig.1 Flowchart of rolling element bearing fault diagnosis by IDMM and EMD

3仿真与实验分析

3.1仿真分析

为了验证本文方法在变转速及齿轮噪源干扰条件下滚动轴承故障诊断的有效性，构造了变转速模式下包含齿轮噪源的滚动轴承故障仿真信号。

变转速条件下的滚动轴承故障信号xbearing的仿真公式如下：

xbearing(t)=

(9)

式中，Am为由故障引起的第m个冲击的幅值；β为结构衰减系数；wr为由轴承故障引起的共振频率，u(t)为单位阶跃函数；tm为第m个冲击发生的时间，可由递推公式(10)确定：

(10)

式中,u为由滚动体滑移带来的故障冲击间隔之间的误差，其取值一般为0.01～0.02；f(t)是轴承转频随时间的变化规律；t0=0；n为每转出现的故障冲击数。

变转速条件下健康齿轮振动信号的仿真公式为：

(11)

式中，j(1,2，…，G)为齿轮啮合倍频的倍数；Xj(t)为第j阶谐波的幅值随时间的变化规律；L为齿轮的齿数；Fg(t)为齿轮转频fg(t)的积分函数；齿轮转频与轴承转频的关系为：fg(t)=τf(t)。设定轴承转频随时间变化的规律为f(t)=2.5t+5；一阶啮合频率峰值X1=0.4，二阶啮合频率峰值X2=4，三阶啮合频率峰值X3=0.3，将齿轮啮合频率的二阶倍频设为峰值啮合倍频，其他参数见表1。

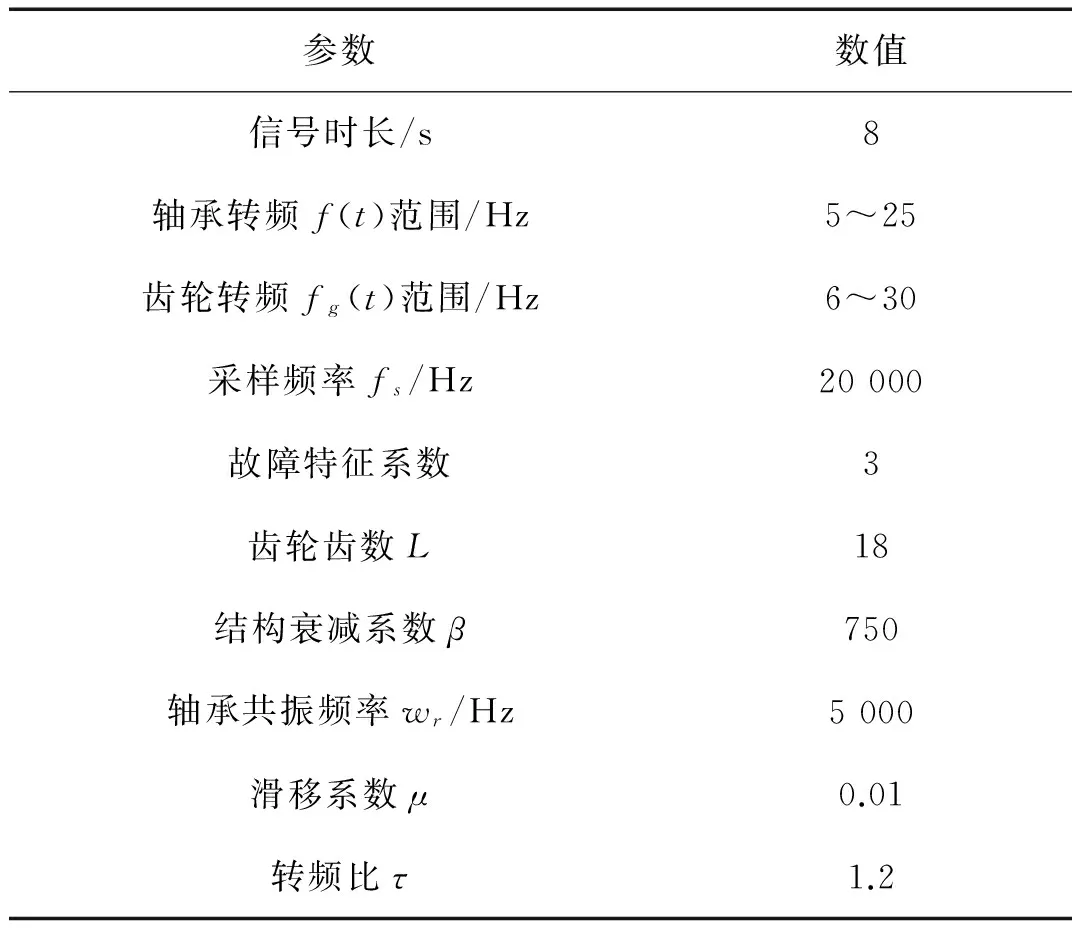
表1　变转速条件下滚动轴承与齿轮混合信号仿真模型参数

选取上述仿真信号4 s时长数据段进行处理，其原始混合信号如图2(a)所示，随着转速的提升，信号的幅值也随之增加。对原始信号进行STFT变换得到时频图，如图2(b)，图2(b)中低频区可以明显辨别出齿轮啮合频率及其倍频，其中预设的二阶IDMM趋势线最为突出。利用峰值搜索算法从时频图中提取IDMM趋势线，图2(c)将IDMM趋势线与预设的齿轮啮合频率进行对比，其中，直线为提取的IDMM趋势线，点划线代表预设的齿轮啮合频率趋势线，虚线代表齿轮啮合频率的2倍频，可以看出，提取的IDMM趋势线与预设的齿轮啮合频率2倍频趋势线几乎相重合，说明可以利用峰值搜索算法从混合信号中提取与齿轮转频有关的频率成分。由于IDMM趋势线与轴承转频有固定的比例关系，根据式(1)以及仿真参数可计算出该固定比例系数为43.2，所以将其等效为轴承转频。

根据IDMM趋势线和混合信号得到重采样信号如图2(e)所示。重采样信号的时频谱如图2(f)所示，从中可以看到重采样后齿轮啮合频率及其倍频在角域趋于平稳。对重采样信号进行包络谱分析得到包络谱如图2(d)，包络谱中含有明显的齿轮啮合频率干扰峰及其二倍频。

对重采样信号EMD分解得到若干IMF，其中图2(h)中给出了前6个IMF分量。分别计算各IMF与重采样信号的互相关系数，表2给出前6个IMF分量的互相关系数，其中IMF1和IMF2互相关系数大于预设的阈值0.5，因此选取IMF1和IMF2，其角域表示分别如图2(j)、(k)所示。分别对IMF1和IMF2进行包络谱分析，如图2(f)、(g)所示。由图2(l)、(m)易辨别IMF1的包络谱为轴承信号的包络谱，其局部放大图如图3所示，该包络谱中存在一阶故障特征阶比(Fault Characteristic Order,FCO)及二阶三阶倍频，对应的横坐标分别为0.069 6， 0.139和0.208 6，以及转频阶比(Bearing Rotational Order,BRO)及其倍频，对应横坐标分别为0.023 2和0.046 16,一阶故障特征阶比峰值对应的横坐标数值与一阶转频阶比横坐标值的比值为3，与预设的故障特征阶比相等，说明该方法能有效的辨别出轴承的故障类型。

另外，图2(g)、(i)分别表示IMF1和IMF2的时频图，图2(g)只含有滚动轴承的故障信息，而图2(i)只含有齿轮啮合频率及其倍频。通过图2(g)、(i)从另一个方面证明本文算法可以有效的将混合信号中的齿轮啮合频率以及轴承故障成分分离。

对比图2(l)和(d)，不难看出本文方法有效去除齿轮噪源干扰的同时，各阶谐波的幅值也有明显的提升，其中一阶故障特征阶比幅值的的变化比例达到113.57%，具体数值及变化幅度如表3所示。

表2　 IMF分量与重采样信号的互相关系数

图2　本文算法的效果流程图Fig.2 The flowchart of all the algorithms with simulation signal

图3　IMF1包络谱的局部放大图Fig.3 Partial enlargement figure of the IMF1envelop spectrum

谐波阶比谱谐波分量幅值未去齿轮噪去齿轮噪变化比例1BRO0.035340.036052%2BRO0.019730.0271137.4%1FCO0.11570.2471113.57%2FCO0.11940.2509110.13%3FCO0.10060.18684.89%4FCO0.078660.125259.17%

3.2实验验证

本文在BR-D单级圆柱直齿减速器试验台上对提出的新方法进行验证，试验台简图如图4所示，齿轮为健康齿轮，减速比为3/11。故障轴承为轴承3，利用电火花切割凹坑模拟轴承外圈点蚀故障，型号为6206，故障轴承的各项参数如表4所示。故障特征系数：

图4　试验台结构简图Fig.4 The diagram of the test rig

轴承型号滚动体数n滚动体直径d/mm节圆直径D/mm接触角α620699.52510

该试验台由速度调节器控制电机(130ZYT-1.5 kw)转速，加速度传感器安装在离轴承较近的位置以准确测量轴承的振动信号，转速计安装在最右侧用于测量转速，采集装置为YE6231采集卡及其配套的采集软件，采样频率设为24 000 Hz。混合信号的时域波形图如图5所示。

利用本文方法对测取的混合振动信号进行分析。图6中直线表示从混合信号的时频图中提取的IDMM趋势线，点划线为测取的齿轮啮合频率趋势线，该趋势线可以根据转速计测量的信息以及式(1)计算得到，虚线为测取的齿轮啮合频率3倍频趋势线。不难看出，IDMM趋势线与测取的IDMM趋势线变化趋势一致，数值上相吻合。利用IDMM趋势线对混合信号进行角域重采样得到重采样信号，对该信号进行包络谱分析得到其包络谱如图7所示，图中箭头所指的突出峰即为齿轮啮合频率的干扰峰及其二倍、三倍频，代表转频的突出峰被淹没在噪声中，难以辨别。

对重采样信号进行EMD分解得到7个IMF分量，计算得到的前7个IMF分量与重采样信号的互相关系数分别为0.664、0.718、0.145、0.014、0.003、0.003和0.001。IMF1和IMF2的互相关系数值大于0.5，则对它们进行包络谱分析，计算结果如图8(a)、(b)所示。图8(a)即为故障轴承的包络谱，该频谱中齿轮噪源的干扰成分被有效消除。图8(a)的局部放大图如图9所示，图中含有明显的代表转频的突出峰，以及故障特征阶比及其倍频。一阶故障特征阶比对应的横坐标数值与转频对应的横坐标数值相比为3.61，实际值为3.66，即可判断该轴承外圈存在故障。利用本文方法得到的滚动轴承包络谱中各阶谐波与重采样信号包络谱中各阶次谐波相比，其幅值的变化比例如表5所示。经过本文方法处理后包络谱中各个谐波的幅值明显增加，最大变化比例达到41.53%。

图5　实测混合信号的时域波形图Fig.5 Mixed measure signal in time domain

图6　实测的齿轮啮合转频及提取IDMM趋势线Fig.6 Extracted IDMM trend and measured gear instantaneous meshing frequency

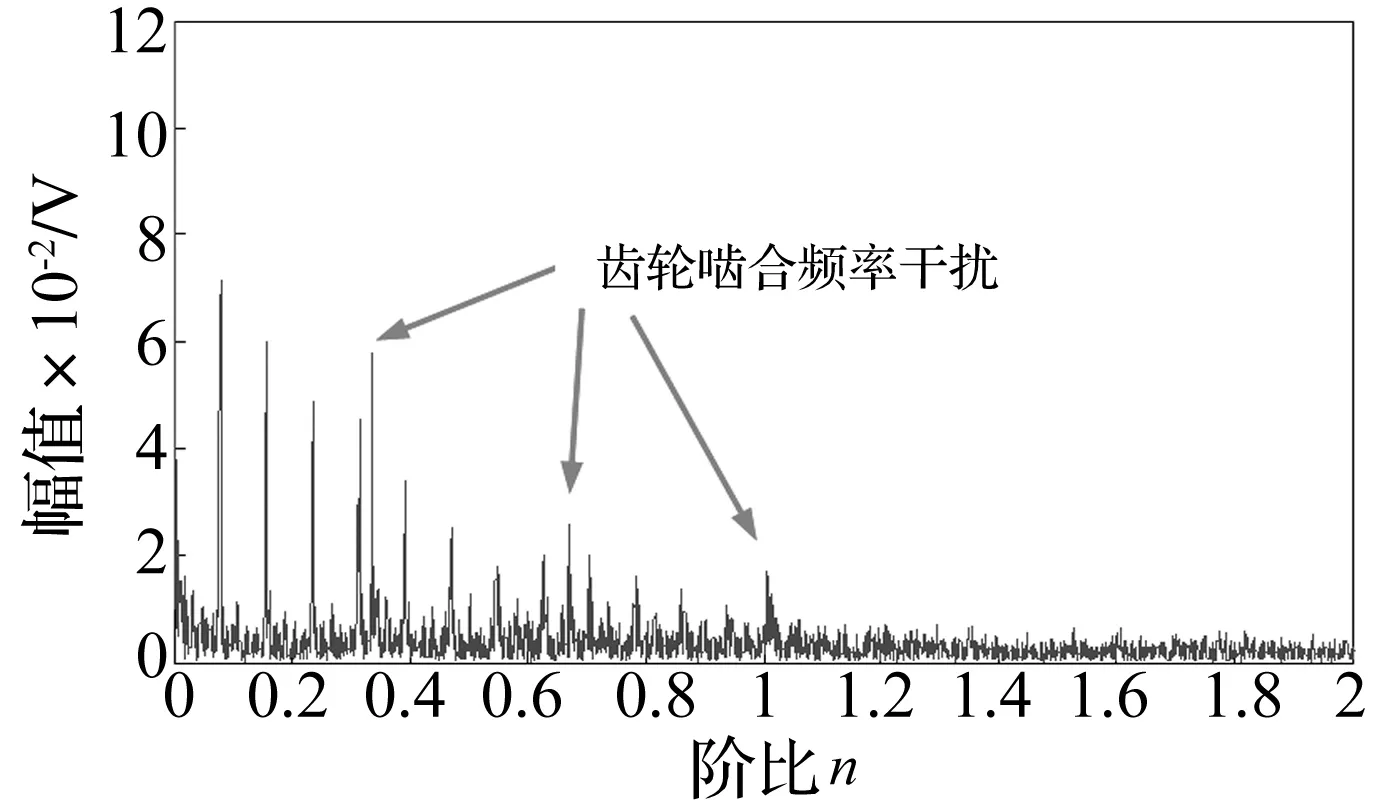
图7　重采样信号的包络谱Fig.7 Envelop order spectrum of resampled signal

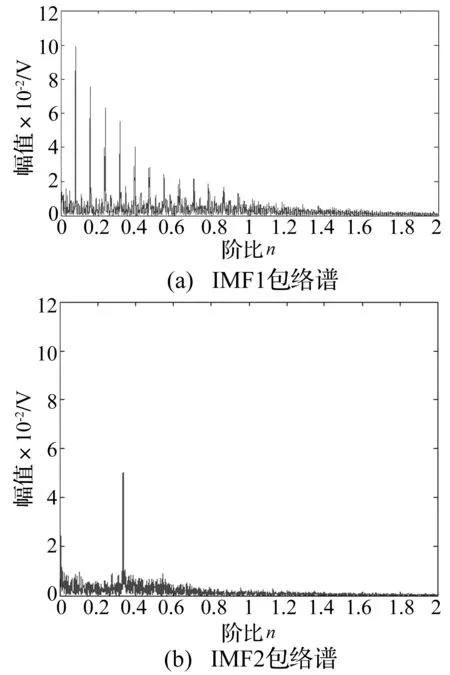
图8　IMF分量的包络谱Fig.8 Envelop spectrum of IMF

图9　IMF1包络谱的局部放大图Fig.9 Partial enlargement figure of the IMF1 envelop spectrum

谐波阶比谱谐波分量幅值未去齿轮噪去齿轮噪变化比例1BRO无0.017272BRO无无1FCO0.065280.0922441.3%2FCO0.05430.0725333.57%3FCO0.0452470.0640441.53%4FCO0.035450.0488237.72%

4结论

本文提出了基于IDMM和EMD变转速及齿轮噪源干扰条件下的滚动轴承故障诊断方法，该方法的优势表现在以下几个方面：

(1) 将IDMM趋势线等效为轴承转频对混合信号进行重采样减少了故障诊断过程对辅助设备的依赖；

(2) 将EMD算法应用于齿轮噪源的去除，实现了混合信号中齿轮噪源与滚动轴承振动信号的分离；

(3) IDMM与EMD方法相结合避免了多次重采样，无需复杂的参数计算，简化了变转速及齿轮噪源干扰下滚动轴承故障诊断的过程。

(4) 利用本文方法得到的包络谱与直接对重采样信号进行包络分析得到的包络谱相比，齿轮信号的干扰峰被有效去除，代表滚动轴承故障特征频率以及转频突出峰的幅值也得到大幅度提高。

需要指出的是对于本文仿真与实测数据分析过程中选取的IMF都为前两个分量，属于巧合现象。另外，本文方法的不足之处表现在其仅适用于齿轮转频与轴承转频有固定比例关系的旋转部件，例如齿轮箱中滚动轴承的故障诊断。

参 考 文 献

[1] 王天杨,李建勇,程卫东.基于改进的自适应噪声消除和故障特征阶比谱的齿轮噪源干扰下变转速滚动轴承故障诊断[J].振动与冲击，2014,33(18):7-13.

WANG Tian-yang,LI Jian-yong,CHENG Wei-dong.Fault diagnosis of rolling bearing under a variable rotational speed and gear vibration noise based on revised ANC algorithm and FCO spectrum[J].Journal of Vibration and Shock,2014,33(18):7-13.

[2] Fyfe K R, Munck E D S. Analysis of computed order tracking[J].Mechanical System And Signal Processing,1997,11(2):187-205.

[3] Cheng Wei-dong,Gao R X,Wang Jin-jiang,et al.Envelope deformation in computed order tracking and error in order analysis[J].Mechanical System and Signal Processing,2014, 48(1/2):92-102.

[4] Bossley K M, Mckendrick R J, Harris C J, et al. Hybird computed order tracking[J]. Mechanical Systems And Signal Processing, 1999,13(4):627-641.

[5] Coats M D, Randall R B. Order-tracking with and without a tacho signal for gear fault diagnostics[C]//Proceedings of Acoustics. Fremantle,Australia, 2012.

[6] 郭瑜, 秦树人, 汤宝平, 等.基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报, 2003,39(3):32-36.

GUO Yu, QIN Shu-ren, TANG Bao-ping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Chinese Journal of Mechanical Engineering, 2003,39(3):32-36.

[7] Randall R B, Antoni J. Rolling element bearing diagnostics—A tutorial[J]. Mechanical Systems and Signal Processing, 2011,25(2):485-520.

[8] Randall R B, Sawalhi N, Coats M. A new methods for separating discrete components from a signals[J]. The Sound and Vibration,2011,45(2):6-9.

[9] Borghesani P, Ricci R, Chatterton S, et al. A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions[J]. Mechanical Systems and Signal Processing, 2013,38(1):23-35.

[10] Wang T,Liang Ming,Li Jian-yong,et al. Bearing fault diagnosis under unknown variable speed via gear noise cancellation and rotational order side band identification[J]. Mechanical Systems Signal and Processing,2015(62/62):30-53.

[11] Huang N E,Shen Zheng,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc Lond A, 1998,454(1971):903-995.

Method for rolling element bearing fault diagnosis based on IDMM and EMD under time-varying rotational speed and gear noise

ZHAO De-zun, LI Jian-yong, CHENG Wei-dong

(School of Mechanical Electronic and Control Engineering, Beijng Jiaotong University, Beijing 100044, China)

Abstract:Time-varying rotational speed and gear noise are the key problems of rolling element bearing fault diagnosis in rotating machinery. For resolving these problems, a new method for rolling element bearing fault diagnosis based on instantaneous dominant meshing multiply(IDMM) and empirical mode decomposition (EMD) was proposed. The new method extracts IDMM from time-frequency representation by peak searching algorithm, then resamples the signal in angle domain, decomposes the resampled signal by EMD, calculates the cross-correlation coefficient between IMFs and resampled signal and selects IMFs by using the threshold value of cross-correlation coefficient. The selected IMFs were then analyzed with envelope spectrum.The effectiveness of the proposed method has been validated by both simulated and experimental bearing vibration signals.

Key words:time-varying speed; gear noise; rolling element bearing fault diagnosis; instantaneous dominant meshing multiply (IDMM); empirical mode decomposition (EMD)

基金项目：国家自然科学基金资助项目(51275030)

收稿日期：2015-04-03修改稿收到日期：2015-05-27

通信作者程卫东 男，博士，副教授，博士生导师，1967年6月

中图分类号:TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.016

第一作者 赵德尊 男，博士生，1990年3月生

E-mail：wdcheng@bjtu.edu.cn