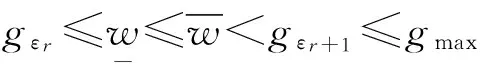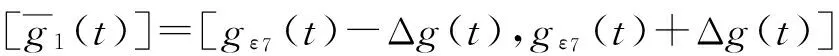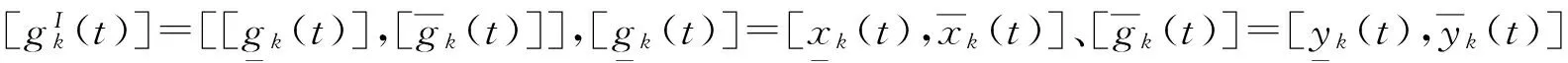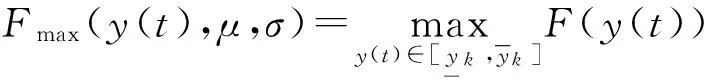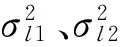随机冲击情况下考虑认知不确定的多态系统可靠性评估

潘　刚， 尚朝轩， 梁玉英， 蔡金燕， 孟亚峰

(军械工程学院 电子与光学工程系，石家庄　050003)

随机冲击情况下考虑认知不确定的多态系统可靠性评估

潘刚， 尚朝轩， 梁玉英， 蔡金燕， 孟亚峰

(军械工程学院 电子与光学工程系，石家庄050003)

摘要：由于环境或其他原因，部件可能受到随机冲击，部件性能退化由正常性能退化和随机冲击两部分构成，对于该类高可靠部件短时间内很难得到足够的性能数据，致使对部件认知存在一定不确定性，无法准确估计系统的可靠性。为实现对系统可靠性的准确估计，假定冲击引起的部件性能损伤分布参数为区间变量，建立基于区间变量的部件性能分布模型，给出了部件状态性能区间连续序列定义和区间状态概率计算方法，对传统的通用生成函数方法进行改进，定义了区间通用生成函数及其运算法则，提出了随机冲击情况下考虑认知不确定的多态系统可靠性评估方法，并以仿真实例进行了验证说明。该方法不仅克服了性能分布信息缺少，无法准确建立状态性能分布模型的不足，且具有很强的通用性和工程应用价值。

关键词：随机冲击；认知不确定性；区间连续序列；区间通用生成函数

20世纪70年代多态系统的概念被提出后[5-6]，基于多态系统模型的系统可靠性研究得到了学者们的广泛关注。在理论方法方面，文献[4, 11-12]对多态系统可靠性的基本概念、评估方法和优化设计等方面内容进行了详细的阐述。在工程应用方面，多态系统可靠性的相关理论已经应用到电力[7-8]、机械[9-10]等领域。一些学者对上述传统的多态系统理论进行推广。Ding等[13-14]在模糊状态和模糊状态概率给定的前提下，给出了模糊多态系统的通用定义和可靠性分析方法。鄢民强等[15]提出了一种考虑不完全覆盖的模糊多状态系统的可靠性计算方法。Li等[16]利用区间分析理论和通用生成函数方法分析了多态系统的区间可靠性。Li等[17]对具有随机冲击情况的考虑竞争失效的多状态系统可靠性模型进行分析。对于具有随机冲击情况的高可靠部件构成的系统，通常情况下，很难准确定量冲击对部件或系统性能的影响。通过对当前上述研究分析可知，在具有随机冲击的情况下，无论是基于 “二态”假设，还是采用多态系统模型，对于随机冲击情况下考虑认知不确定的多态系统可靠性分析研究相对较少。

高可靠性部件构成的多态系统进行可靠性分析时，随机冲击情况下的认知不确定性主要表现在两个方面：①随机冲击对部件性能分布的影响具有一定的不确定性，且很难准确定量；②由于对系统或部件性能退化机理认知的不完善，而建立的状态性能分布模型往往是不准确的，有时可能会出现很大的偏差。鉴于上述不足，本文提出了随机冲击情况下考虑认知不确定的多态系统区间可靠性分析方法，给出了多态系统的可靠性分析流程，并以仿真实例进行了验证分析。

1性能退化系统状态分析

1.1性能退化部件性能分析

对随机冲击情况下考虑认知不确定的部件性能分布进行分析之前，先做如下假设：

(2) 部件只有一个性能参数x，对应一个性能退化过程，且退化过程不可逆。

(3) 定义N(t)为到t时刻为止部件受到的冲击次数，Sl为第l次冲击对部件性能的损伤，S(0)=0，S(t)为到t时刻为止，随机冲击对部件性能产生的累计损伤，则：

假设冲击次数服从参数为λ的泊松分布，即

(5) 在任意时刻t，假设部件性能X(t)服从均值为μ(t)，方差为σ(t)2的正态分布，其概率密度函数为f(x;θ(t))。

(6) 同时考虑正常的性能退化和冲击所引起的性能退化时，t时刻部件的性能可以表示为：

此时部件的性能分布函数为：

F(Y)=p{G(t)≤y}=

由于，

最后可得:

(1)

式中，

1.2性能退化部件状态概率分析

定义部件的状态性能区间划分准则，采用系统最低任务需求[w]与部件性能分布特性相结合的方法对部件的状态性能区间进行划分，具体如下：

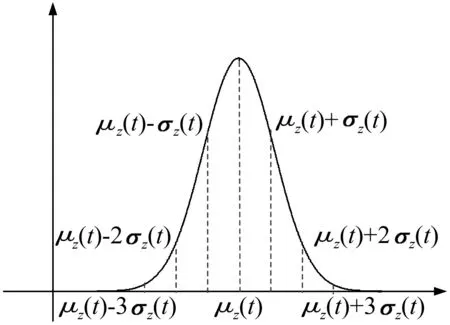
图1　部件性能分布Fig.1 Performance distribution of components

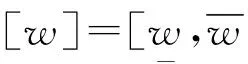
(4) 令部件的最大性能为gmax，为了便于表示假定gε1(t)=μz(t)-3σz(t)，gε2(t)=μz(t)-2σz(t)，gε3(t)=μz(t)-σz(t)，gε4(t)=μz(t)，gε5(t)=μz(t)+σz(t)，gε6(t)=μz(t)+2σz(t)，gε7(t)=μz(t)+3σz(t)。

其中，

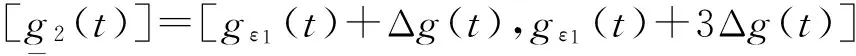
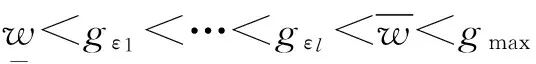
其中，

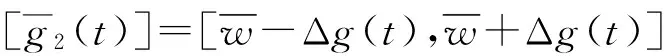
gεx(t)=(gε1(t)+gεl(t))/2，l=1,…,7

其中，

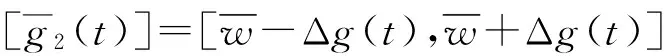
gεx(t)=(gεr+1(t)+gεl(t))/2，1≤r

其中，

其中，

⑥ 当[w]>gmax时，表明部件的性能已不满足系统分配的最小任务需求，对其进行状态的划分已经没有实际的工程意义，故此时可认为部件失效。

(2)

式中，

2运算法则

为了降低计算的难度，在分析时将状态性能区间连续序列分为区间连续序列上限、区间连续序列中值、区间连续序列下限三种情况进行讨论分析，现以区间连续序列上限为例进行分析说明。

2.1区间通用生成函数定义

部件i的状态概率区间族形式为：

{pi(t)}={[p1(t)],…,[pki(t)],…,[pMi(t)]}

定义部件i的区间通用生成函数为：

(3)

式中，i=1,2,…,n，ki=1,2,…,Mi。

2.2区间通用生成函数运算法则

U(t,z)=Ω(ui(t,z),uj(t,z))=

(4)

根据系统结构特点定义如下运算符：

δ1(ui(t,z),uj(t,z))=

δ2(ui(t,z),uj(t,z))=

3基于区间通用生成函数的多态系统可靠性分析

根据上述运算法则的分析，假定得到的多态系统区间通用生成函数为：

(5)

定义多态系统的最小区间任务性能需求为[w]，则系统的区间可靠度为：

[R(t)]=P{[G(t)]≥[w]}=

(6)

式中，P{[G(t)]≥[w]}表示[G(t)]-[w]≥0的概率，[G(t)]={[g1(t)],…,[gks(t)],…,[gMs(t)]}。

综合上述三点，可以将[gks(t)]-[w]的可能度区间定义为：

p([gks(t)]-[w]≥0)=

因此，系统的区间可靠度为：

[R]=P{[G(t)]≥[w]}=

4算例分析

图2　多态串-并联系统Fig.2 Multi-state serial-parallel system

4.1部件和分系统区间通用生成函数

4.1.1部件区间通用生成函数

表1　部件退化性能、分系统结构函数和系统结构函数

部件6可分为2个状态，其状态性能定义为g6={[0,70],[70,100]}。

在t=10 000 h时，根据2.2节性能退化部件状态概率分析，部件各状态性能区间连续序列对应的概率区间为：{p1(t)}={p1,1(t),p1,2(t),p1,3(t)}，其中，p1,1(t)=[0.004 4,0.008 2]，p1,2(t)=[0.064 5,0.107 8]，p1,3(t)=[0.836 2,0.884 0]{p2(t)}={p1(t)}，{p3(t)}={p31(t),p32(t)}，其中，p3,1(t)=[0.037 1,0.049 5]p3,2(t)=[0.935 0,0.950 5]{p3(t)}={p4(t)}={p5(t)}，{p6(t)}={p6,1(t),p6,2(t)}，p6,1(t)=0.051 8，p6,2(t)=0.948 2。

以状态性能区间连续序列上限方法为例对部件区间通用生成函数和分系统区间通用生成函数进行分析，其他的方法类似，不再赘述。

根据状态性能区间连续序列族定义和性能退化部件状态概率求解方法，可得部件1～6的区间通用生成函数为：

u1(t,z)=[0.004 4,0.008 2]z[51.97,52.47]+

[0.064 5,0.107 8]z[54.75,55.25]+

[0.836 2,0.884 0]z[69.75,70.25]，

u2(t,z)=u1(t,z),

u3(t,z)=[0.037 1,0.049 5]z[34.77,35.07]+

[0.935 0,0.950 5]z[49.85,50.15]，

u3(t,z)=u4(t,z)=u5(t,z)，

u6(t,z)=[0,70]z0.051 8+[70,100]z0.948 2

4.1.2分系统区间通用生成函数

由图2可知分系统1是由部件1和部件2构成，且分系统1的性能为部件1和部件2性能的和，根据第3节运算法则定义的δ1运算符，可得分系统1的区间通用生成函数为：

Usub1(z,t)=δ1(u1(z,t),u2(z,t))=

[0.000 6,0.001 8]z[106.7,107.7]+

[0.004 2,0.011 6]z[109.5,110.5]+

[0.007 4,0.014 4]z[121.7,122.7]+

[0.107 8,0.190 6]z[124.5,125.5]+

[0.699 2,0.781 6]z[139.5,140.5]

分系统2是由部件3、4和5构成，且其性能为部件3、4和5性能的和，同理可得分系统2的区间通用生成函数为：

Usub2(z,t)=δ1(u3(z,t),u4(z,t),u5(z,t))=

[0,0.000 1]z[104.3,105.2]+[0.003 9,0.007 0]z[119.4,120.3]+

[0.097 3,0.134 2]z[134.5,135.4]+

[0.817 3,0.858 7]z[149.6,150.5]

4.2系统区间可靠性分析

4.2.1系统区间可靠性分析

将分系统1和分系统2采用第2节运算法则定义的δ2运算符，可得分系统1、2综合后的分系统区间通用生成函数为：

U1-2=[0.000 4,0.001 5]z[106.7,107.7]+

[0.003 7,0.011 3]z[109.5,110.5]+

[0.003 1,0.006 9]z[119.4,120.3]+

[0.006 8,0.014 3]z[121.7,122.7]+

[0.098 6,0.189 2]z[124.5,125.5]+

[0.068 0,0.104 9]z[134.5,135.4]+

[0.571 4,0.671 2]z[139.5,140.5]

因此，根据式(7)可得分系统1和2的区间可靠度为：

R1-2=[0.752 1,0.999 4]

分系统3的可靠度为：

R3=0.948 2

最后可得t=10 000 h时系统的区间可靠度为：

R(t)=R1-2(t)R3(t)=[0.713 2,0.947 7]

在t=10 000 h时采用Monte Carlo(MC)仿真方法进行分析，在分析过程中为了充分描述Monte Carlo(MC)仿真方法在每次仿真计算过程中所得计算结果的可能性，取L=1 000次仿真结果的最大值和最小值，将其作为区间可靠度的最大值和最小值，可得MC仿真方法的区间可靠度为[0.894 8,0.956 9]。

如果采用传统的方法进行系统可靠性分析，则一般假设部件仅有两个状态，根据系统总的性能输出要求，确定部件的失效阈值。对于部件1,2性能不小于[54.75, 55.25]时分系统1正常，部件3,4,5性能不小于[35.75,36.25]时分系统2正常，部件6的性能不小于70时，分系统3正常，因此，采用传统方法可得系统的区间可靠度为[0.483 4,0.606 3]。

采用本文所提方法、传统可靠性方法、Monte Carlo仿真方法所得系统的区间可靠性对比关系如表2所示。

表2　三种方法所得系统区间可靠性对比分析结果

通过对表2分析我们可以得出以下结论：

1) 采用本文所提方法，分别对连续区间序列下限、中值、上限进行分析，所得计算结果总体上呈增大的趋势，连续区间序列的上限方法和下限均未完全包含连续区间序列中的状态信息，而连续区间序列的中值为上限和下限的折中，故所得结果一定程度上，更加接近客观值，取连续区间序列族下限时所得结果随着时间的增加与后两者的偏差越大，在后续研究中不再分析。

2) 传统方法、区间连续序列中值方法和Monte Carlo仿真方法三者所得结果进行对比，传统方法与后两者相比误差较大，且采用传统方法进行系统可靠性估计时，部件的失效阈值通常是根据部件自身的统计规律确定的，不能根据具体系统具体分析，有时可能会出现一些偏差，进一步体现了多态系统理论在描述系统可靠性时的准确性优势。

4.2.2状态性能区间半径影响分析

图3　区间半径大小与系统区间可靠度均值的关系Fig.3 The relationship between interval radius and the mean of system interval reliability

由图3可以得出以下结论：

1) 连续区间序列上限方法的最大值点和最小值点分别为(0,0,0.948 1)、(2,2,0.701 4)；连续区间序列中值方法的最大值点和最小值点分别为(0,0,0.904 7)、(2,2,0.648 3)。

2) 对于连续区间序列上限方法和连续区间序列中值方法，随着参数α，β值的增加，系统区间可靠度均值呈增大趋势，其主要原因是当α=β=0，区间连续序列退化为点区间，部件状态性能区间中存在的不确定性变为0，再对其采用区间序列上限方法时，其取值变为点区间的上边界，致使[gks(t)]-[w]的可能度增大，从而使得区间可靠度的均值增大，同理，区间序列中值法亦是如此。

4.3进一步分析

4.3.1部件状态点区间划分时系统可靠性分析

为了充分分析本文所提方法的优缺点，在t=10 000 h时，将部件状态按传统的点区间进行划分，部件的通用生成函数为：

u1(z,t)=u2(z,t)=0.002 7z[0,51.6]+

0.093 4z[51.6,55]+0.903 8z[55,70]

u3(z,t)=u4(z,t)=u5(z,t)=

0.039 4z[0,34.8]+0.960 6z[34.8,50]

分系统1和分系统2的区间通用生成函数分别为：

Usub1(z,t)=δ1(u1(z,t),u2(z,t))=

0.000 5z[51.6,106.6]+0.004 9z[55,106.6]+

0.008 7z[103.2,121.6]+0.168 9z[106.6,125]+0.817 0z[110,140]

Usub2(z,t)=δ1(u3(z,t),u4(z,t),u5(z,t))=

0.000 1z[0,104.5]+0.004 5z[34.8,119.7]+

0.109 1z[69.7,134.8]+0.886 3z[104.5,150]

将分系统1、2综合后的分系统区间通用生成函数为：

U1-2=0.000 1z[0,104.5]+0.000 5z[51.6,106.6]+

0.004 9z[55,110]+0.004 5z[34.8,119.6]+

0.007 7z[103.2,121.6]+0.149 7z[104.5,125]+

0.089 2z[69.7,134.8]+0.724 1z[104.5,140]

当系统的最小性能需求[w]=[90,110]，则分系统12的可靠度为：R1-2=0.837 7。最后可得系统的可靠度为：

R(t)=R1-2(t)R3(t)=0.794 4

4.3.2进一步对比分析

为了进一步对比分析，将区间连续序列上限方法(状态3-2)和区间连续序列中值方法(状态3-2)两种方法结果的均值，点区间方法、传统方法和Monte Carlo仿真方法的结果进行比较。

图4　几种方法所得可靠性结果对比Fig.4 Comparison of reliabilities respectively obtained by the afore-said methods

由图4可以得出以下结论：

1) 在传统方法中，部件失效阈值的选取对系统可靠性的影响较为敏感，因此其成为影响系统可靠度评估精度的薄弱环节，与其他方法相比误差较大。

2) 区间连续序列中值方法(状态3-2)和点区间方法两种方法所得结果相对比较保守，此外状态数相同的情况下，因大部分系统的失效率随着时间的增加逐渐增大，即可靠性降低的速率要增大，故采用区间连续序列中值方法要比点区间方法更加符合系统可靠性的退化规律，精度更高，一定程度上克服了随着状态数的增加，计算过程过于繁琐的不足。

3) 区间连续序列上限方法(状态3-2)与Monte Carlo仿真方法结果相对存在一定的误差，随着时间的增加偏差增大，原因主要在于仿真的过程中部件的状态数N=20相对较少，若部件的状态数过多的话，在仿真计算系统的状态数过于庞大，难以计算。

众所周知，采用通用生成函数方法对多态系统可靠性进行分析时，随着状态数的增加，精度增大，但计算的复杂度增加，下面将分析分系统1中部件状态为4，分系统2中部件状态为3时，系统区间可靠度和区间可靠度均值随时间的变化关系，见图5。

图5　部件状态取不同值时系统可靠性的变化Fig.5 Changes of MSS reliability when component’ state number is changed

由表3和图5可以得出以下结论：

1) 状态数(4-3)与状态数(3-2)相比，在相同时刻，状态数(4-3)中区间连续序列下限方法和区间连续序列中值方法的分析结果呈增大的趋势。

2) 区间连续序列中值方法与Monte Carlo仿真方法相比结果虽存在一定误差，但在一定程度上可以表征系统的可靠性水平，因此在损失一定的精度情况下，本文区间连续序列族中值方法不仅解决了传统方法误差大的问题，而且克服了Monte Carlo仿真方法仿真规模大、耗时长的不足，方法简单，便于实现。

3) 采用区间通用生成函数方法随着状态数的增加，降低了系统的可靠性评估结果与MC仿真方法所得评估结果之间的误差，因此在一定程度上验证随着部件状态数的增加，系统可靠性评估结果精度增大的结论。

表3　状态数(4-3)时所得系统区间可靠性对比分析结果

5结论

本文针对考虑认知不确定性与随机冲击情况的多态系统，提出了随机冲击情况下考虑认知不确定的多态系统区间可靠性分析方法，给出了多态串-并联系统可靠性的分析流程，通过仿真实例分析可得出以下结论：

(1) 该方法降低了传统方法中部件失效阈值选取不当对系统可靠度评估影响，提高了系统可靠性评估精度；

(2) 该方法在状态数相同的情况下，与传统点区间通用生成函数法相比，不仅精度较高，且一定程度克服了其随着状态数的增加，计算过程过于繁琐的不足；

(3) 该方法与Monte Carlo仿真方法相比，克服了其仿真规模大、耗时长的不足。

参 考 文 献

[1] Nakagawa T. Shock and damage models in reliability theory[M]. Berlin:Springer, 2006.

[2] Liu Y, Huang H, Pham H. Reliability evaluation of systems with degradation and random shocks, 2008[C]//Reliability and Maintainability Symposium.Las Vegas,NV:RAMS,2008.

[3] Wang Ya-ping. Multi-objective impact for dependent competing system with multiple degradation progress and random shock[D]. New Brunswick,NJ:The State University of New Jersey, 2012.

[4] Lisnianski A, Levitin G. Multi-state system reliability: assessment, optimization and applications[M]. Singapore: World Scientific, 2003.

[5] Barton R M, Damon W. Reliability in a multi-state system[C]//Procedings of the 6th Annual Southeastern Symposium on Systems Theory. Baton Rouge,LA，1974.

[6] Barton R E, Wu A S. Coherent systems with multi-state components[J]. Mathematica of Operations Research, 1978(3):275-281.

[7] Li Y, Zio E. A multi-state model for the reliability assessment of a distributed generation system via universal generating function[J]. Reliability Engineering and System Safety, 2012(106):28-36.

[8] Billinton R Y G. Adequacy assessment of composite power generation model for reliability evaluation.[J]. International Journal of Reliability and Safety, 2008,2(1):79-98.

[9] 史新红, 齐先军, 王治国. 基于UGF的发电系统区间可靠性评估及其仿射算法改进[J]. 合肥工业大学学报:自然科学版, 2014,37(3):286-291.

SHI Xin-hong，QI Xian-jun，WANG Zhi-guo. Interval reliability estimation of power generating system based on UGF method and its modification by using affine arithmetic[J]. Journal of Hefei University of Technology:Natural Science, 2014,37(3):286-291.

[10] 尚彦龙, 蔡琦, 赵新文,等. 基于UGF和Semi-Markov方法的反应堆泵机组多状态可靠性分析[J]. 核动力工程, 2012(1): 117-123.

SHANG Yan-long, CAI Qi, ZHAO Xin-wen, et al.Multi-state reliability for pump group in nuclear power system based on UGF and semi-markov process[J]. Nuclear Power Engineering,2012(1):117-123.

[11] Natvig B. Multistate systems reliability theory with applications[M]. Hoboken, NJ, USA: Wiley,2010.

[12] Levitin G. The universal generating function in reliability analysis and optimization[M]. London: Springer, 2005.

[13] Ding Y, Zuo M J, Lisnianski A,et al.Fuzzy multi-state systems: general definitions, and performance assessment[J]. IEEE Transactions on Reliability, 2008,57(4):589-594.

[14] Ding Y, Lisnianski A. Fuzzy universal generating functions for multi-state system reliability assessment[J]. Fuzzy Sets and Systems, 2008，159:307-324.

[15] 鄢民强, 杨波, 王展. 不完全覆盖的模糊多状态系统可靠性计算方法[J]. 西安交通大学学报, 2011,45(10):109-114.

YAN Min-qiang, YANG Bo, WANG Zhan. Reliability assessment for multi-state system subject to imperfect fault coverage[J].Journal of Xi’an Jiaotong University, 2011,45(10): 109-114.

[16] Li Chun-yang,Chen Xun, Yi Xiao-shan,et al. Interval-valued reliability analysis of multi-state systems[J]. IEEE Transactions on Reliability, 2011,60(1):323-330.

[17] Li W, Pham H. Reliability modeling of multi-state degraded systems with multi-competing failures and random shocks[J]. IEEE Transactions on Reliability, 2005,54(2):297-303.

[18] 邱志平. 非概率集合理论凸方法及其应用[M]. 北京: 国防工业出版社, 2005.

Estimation of interval-valued reliability of multi-state system in consideration of epistemic uncertainty under random shock

PAN Gang, SHANG Chao-xuan, LIANG Yu-ying, CAI Jin-yan, MENG Ya-feng

(Department of Electronic and Optic Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

Abstract:Components may suffer from random shocks in some environments or other conditions. The performance degradation of components consists of normal performance degradation and random shocks. Since it is hard to obtain adequate performance data of high-reliability components within a short time, there are epistemic uncertainties on components and the system reliability cannot be accurately estimated. For the purpose of accurate estimation of system reliability, the distribution parameters of components’ performance deterioration caused by random shocks were assumed as interval variables, the components’ performance distribution model based on the interval variables was built, the definition of interval-continuous sequences of components’ state performances was presented and a method to calculate the interval-valued state probability were provided. The traditionally universal generating function method was improved, the interval-valued universal generating function and its algorithm were defined, a method to assess multi-state system reliability in consideration of epistemic uncertainty under random shocks was proposed, and the verification and illustration were conducted by using simulations. The method not only overcomes the inaccuracy of the reliability analysis model, but also has strong versatility and engineering application value.

Key words:random shock; epistemic uncertainty; interval-continuous sequence; interval-valued universal generating function

基金项目：国家自然科学基金(61372039;61271153)

收稿日期：2015-04-02修改稿收到日期：2015-05-31

通信作者尚朝轩 男，博士，教授，博士生导师，1964年4月生

中图分类号:N945;TB114.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.005

第一作者 潘刚 男，博士生，1987年7月生