一种基于LMS的振动信号相位差自适应无偏估计方法及应用

杨辉跃, 涂亚庆, 张海涛, 李　明

(后勤工程学院 信息工程系，重庆　401311)

一种基于LMS的振动信号相位差自适应无偏估计方法及应用

杨辉跃, 涂亚庆, 张海涛, 李明

(后勤工程学院 信息工程系，重庆401311)

摘要：针对振动信号相位差估计问题，提出了一种基于LMS的自适应无偏估计方法。该方法通过一路信号与其正交的三角运算来配准另一路信号，相位差的正切值等于两个配准系数之比；根据均方误差最小原则对配准系数进行迭代更新，从而实现相位差自适应估计；理论推导出噪声引起的估计偏差，并据此对估计结果进行偏差补偿，实现相位差无偏估计，给出了补偿公式和方法流程。实验结果表明：该方法能准确估计出两路同频振动信号相位差，经偏差补偿后估计精度显著提高；在相位差发生突变时，能进行快速跟踪测量，具有较好动态测量特性；该方法在变化流量下科氏流量计振动信号相位差估计中的应用，验证了方法的工程实用性。

关键词：相位差; 自适应; 无偏估计; LMS算法; Hilbert变换

相位差测量技术在振动分析、故障诊断、电力系统、仪器仪表、智能控制等诸多领域应用中有着重要意义[1-3]。现有诸如过零鉴相[4]、数字相关[5-6]、DFT谱分析[7]等方法在动态相位差估计方面存在各自不足。过零鉴相法利用两路信号过零点的时间计算相位差，计算速度快，但硬件成本高；数字相关法利用两路信号的相关函数估计相位差，对随机噪声抑制能力强，但受谐波影响较大且要求同步采样；DFT谱分析将信号从时域变换到频域，利用相频关系估计相位差，应用广泛，但受谱泄漏影响。最小均方(LMS)自适应算法[8]由于无需信号先验知识，且计算简便，易于实现，广泛应用于自适应滤波器、频率跟踪、时延估计等领域[9-12]。文献[13]通过自适应相位计跟踪信号相位变化，利用两个相位计的估计值之差实现相位差估计，但难以估计动态相位差；文献[14]通过对输入信号进行自适应延迟补偿，使得补偿后的信号与参考信号对齐，并在最小均方误差准则下对延迟补偿因子进行计算和修正，由延迟补偿因子获得相位差，但受噪声影响存在估计偏差。

本文利用一路信号与其正交变换来配准另一路信号，并根据最小均方误差对配准系数进行自适应更新，针对估计偏差问题在迭代过程中进行了偏差补偿，实现相位差自适应无偏估计。

1方法原理

1.1基本思想

设两路同频实正弦信号采样序列为s1(k),s2(k)：

k=1,2,…,N

(1)

式中，A为信号幅值，θ1,θ2为初始相位，角频率ω0=2πf0/fs，fs为采样频率，n1(k)和n2(k)是零均值，方差为σ2的高斯白噪声，N为采样长度。

(2)

估计误差：

ε(k)=Asin(ω0k+θ1)-ws(k)Asin(ω0k+θ2)-

wc(k)Acos(ω0k+θ2)+n3(k)

(3)

系数ws(k)和wc(k)中蕴涵相位差Δθ信息，利用LMS算法对ws(k)和wc(k)进行自适应更新，在均方误差E[ε2(k)]→min时即可解算出相位差Δθ。

1.2相位差计算

Δθ=θ1-θ2=arctan(wc/ws)

(4)

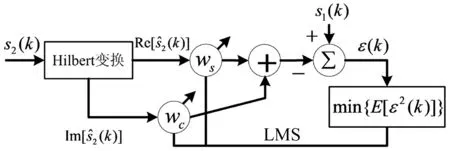
图1　相位差自适应估计原理Fig.1 Principle of the phase difference adaptive estimation

1.3自适应更新

对ws(k)和wc(k)采用LMS最大梯度迭代算法进行自适应计算，有：

(5)

式中，μ为步长。

1.4估计偏差与补偿

由于噪声影响，式(5)的计算结果通常存在偏差。稳态条件下，设

ws(k)≈ws0,wc(k)≈wc0

δws(k)=ws(k)-ws0,δwc(k)=wc(k)-wc0

(6)

代入式(3)，整理可得：

ε(k)=-δws(k)Asin(ω0k+θ2)-

δwc(k)Acos(ω0k+θ2)+n3(k)

(7)

考虑噪声，对式(5)两边同时减去ws0或wc0，得：

δws(k+1)=δws(k)-με(k)s2(k)

(8)

两边取期望，有，

E[δws(k+1)]=E[δws(k)]-μE[ε(k)s2(k)]=

(9)

稳态条件下，一般有

E[δws(k+1)]|k→∞=

E[δws(k)]|k→∞=E[δws(∞)]

(10)

考虑到噪声相关性，联合式(9)和(10)有：

(11)

同理，可得：

(12)

可见，相位差估计是有偏的，偏差大小与信噪比SNR、步长μ以及对ws(k)和wc(k)的稳态值有关。

稳态下，则偏差补偿算法为

ws(k+1)=(1+G)ws(k)-με(k)s2(k)

(13)

式中，G=2σ2/μA2。

1.5方法流程

综上所述，方法流程如图2所示，具体步骤如下：

步骤1信号采样，获取离散序列s1(k)和s2(k)；

步骤2初始化参数wc(0),ws(0)和步长μ，估计信噪比SNR；

步骤6根据式(13)对参数ws(k)和wc(k)进行自适应更新；

步骤7计算相位差Δθ=arctan(wc/ws)。

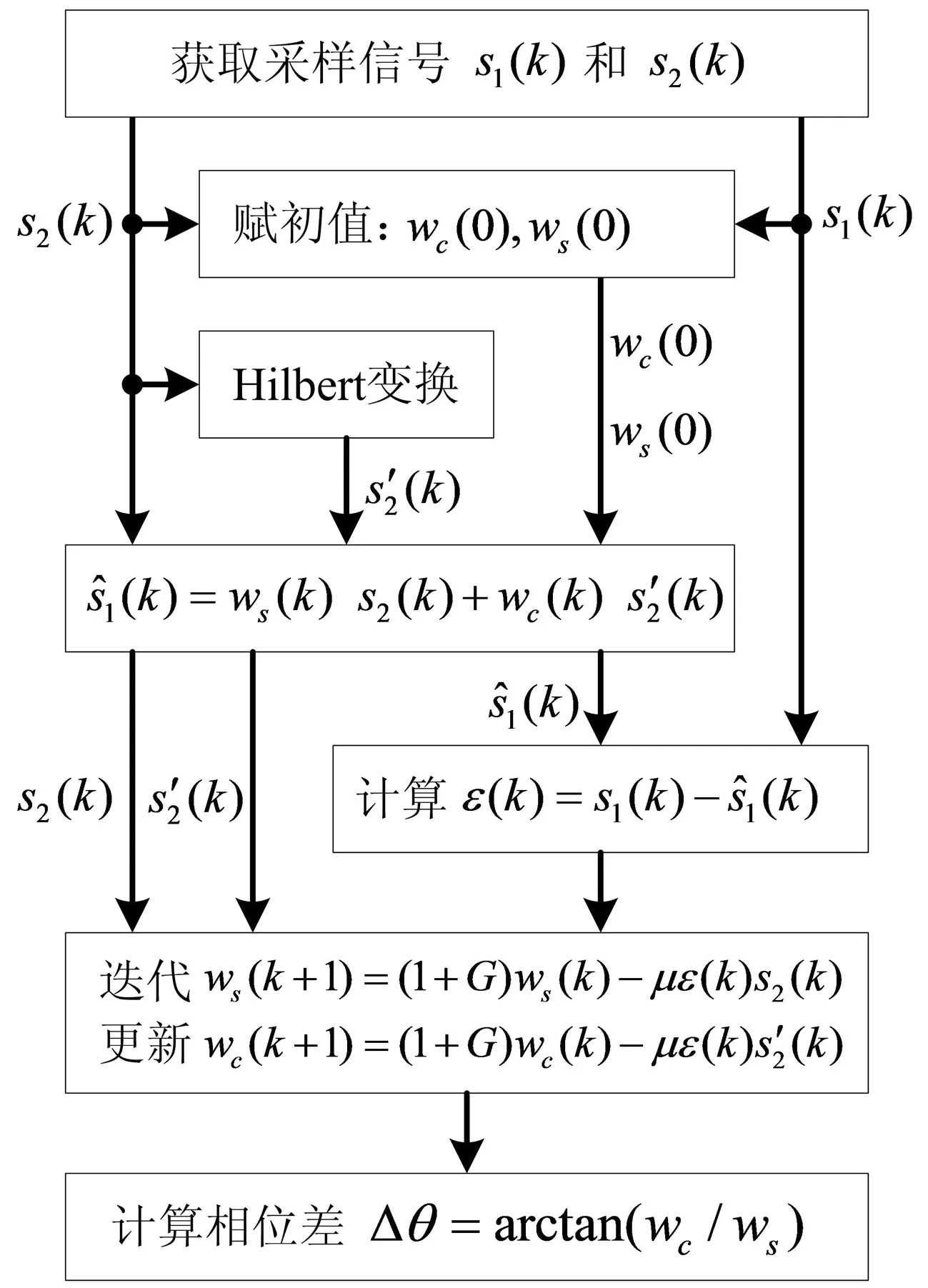
图2　相位差自适应估计流程Fig.2 Flow of the phase difference adaptive estimation

2性能分析

(14)

以下分析均方误差

μ2E[{ε(k)s2(k)}2]

(15)

结合式(11)，可推导出

(16)

(17)

(18)

同理，可得

(19)

联立式(18)和式(19)解得：

(20)

3实验结果

3.1仿真实验

设信号频率f=198 Hz，幅值A=10，相位差分别Δθ=[π/6,π/4,π/3]，SNR=30 dB，采样频率fs=20 000 Hz，初始化步长μ=0.48×10-4，利用本文方法估计相位差，得到估计结果如图3所示。表1给出了稳定后的估计值、均方差及比值校正后的相位差估计值。由实验结果可知，本文方法能准确估计出同频信号相位差，稳态精度与比值校正法持平；校正前存在显著偏差，均方误差为13.832 7，经偏差校正后均方误差为0.081 4，估计精度明显提高。

图3　相位差跟踪结果Fig.3 Phase difference estimation

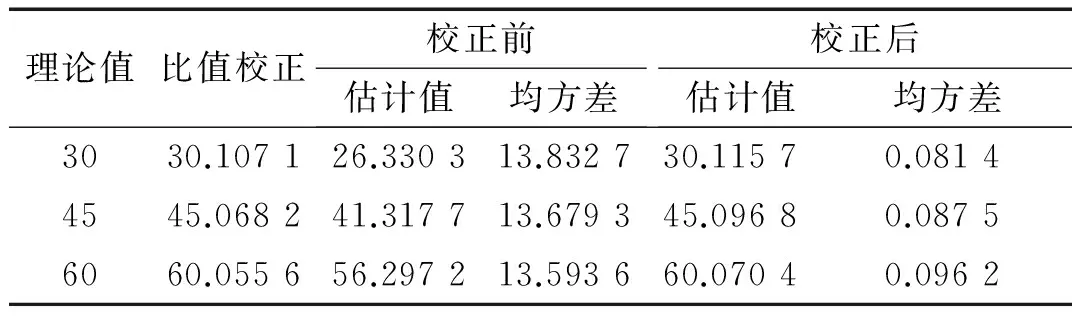
理论值比值校正校正前估计值均方差校正后估计值均方差3030.107126.330313.832730.11570.08144545.068241.317713.679345.09680.08756060.055656.297213.593660.07040.0962

自适应算法中步长μ影响收敛速度和稳定精度，μ值越大收敛越快，但稳态精度降低，反之则稳态精度高、收敛速度慢。图4为不同步长下相位差估计的稳态精度，可见在校正后方法精度更高。

图4　不同步长下相位差估计均方误差Fig.4 MSEs of phase difference estimation at different steps

图5给出了不同信噪比下相位差估计结果。信噪比较低时，偏差校正效果明显，当SNR>30 dB时，信噪比已非影响精度的主要原因，校正前后精度基本一致。

图5给出了相位差突变时本文方法校正前后的跟踪结果。相位差发生突变时，本文方法能实现有效的跟踪测量，且收敛速度快。

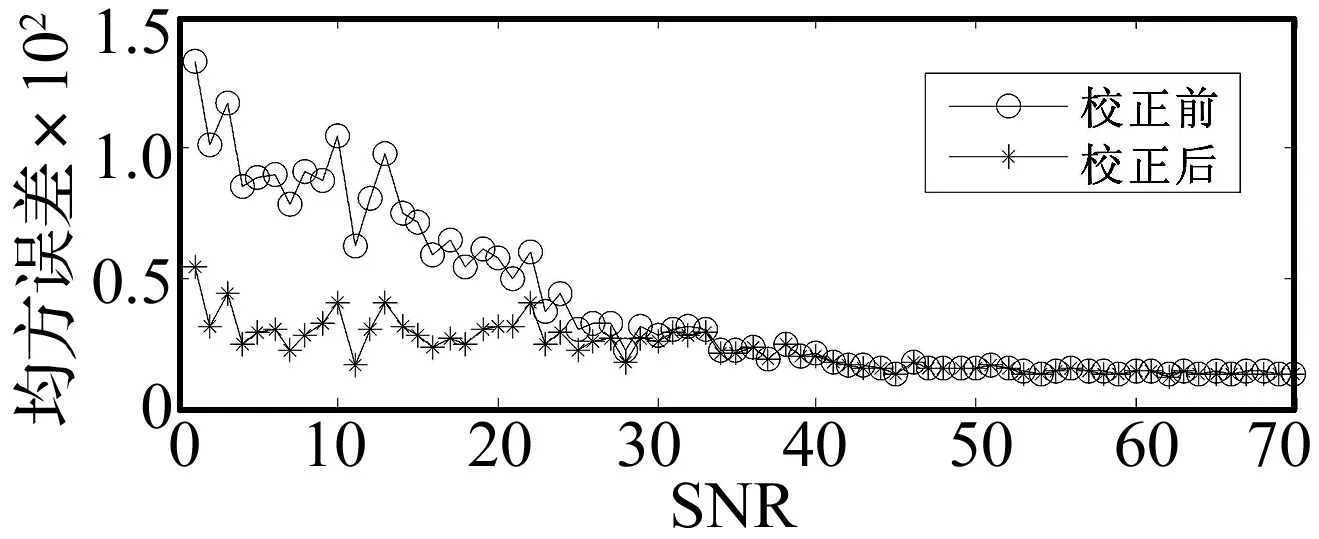
图5　不同信噪比下相位差估计均方误差Fig.5 MSEs of phase difference estimation at different SNRs

图6　时变相位差跟踪结果Fig.5 Estimation of time-vary phase difference

3.2应用实验

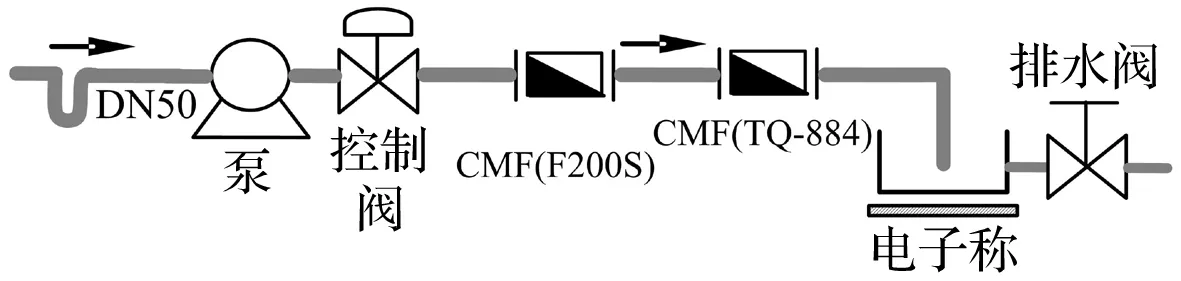
图7　科氏流量计实验平台Fig.7 Experiment equipment of Coriolis mass flowmeter

科氏流量计通过测量管两路振动信号的相位差(时间差)来测量流体的质量流量。利用图7所示科氏流量计实验装置进行应用验证，其中罗斯蒙特F200S型科氏流量计(配1700型变送器，带MVD技术)振动信号频率为197.75 Hz。利用NIUSB9234多通道数据采集器，以采样频率10 kHz采集水流量下科氏流量计振动信号。采集开关阀过程中，流量变化下科氏流量计振动信号。图8给出了4 000点的采样波形，可见科氏流量计信号较为干净。利用本文校正方法跟踪相位差变化，图9给出了示值流量分别从105.2 kg/min和42.7 kg/min到0 kg/min过程中，本文方法估计的相位差变化。采用流量计示值作为参考，推导出相位差变化趋势及幅度与本文方法估计值吻合，说明本文方法在科氏流量计信号处理应用中是有效可行的。

图8　科氏流量计信号时域波形Fig.8 Signals of Coriolis mass flowmeter

图9　流量变化时相位差估计曲线Fig.9 Phase difference estimation when flow changes

4结论

针对同频信号相位差估计问题，本文提出了一种基于LMS的相位差自适应无偏估计方法。给出了方法的基本思想、相位差估计和偏差校正公式，给出了方法流程，并分析了方法性能。实验结果表明本文方法能准确估计出振动信号相位差；在相位差发生突变时，能进行快速跟踪测量，具有较好动态测量特性；科氏流量计应用实验验证了本文方法的工程实用性。后续研究将围绕进一步提高估计精度展开。

参 考 文 献

[1] Dash P K, Krishnanand K R, Patnaik R K. Dynamic phasor and frequency estimation of time-varying power system signals[J]. Electrical Power and Energy Systems, 2013,44:971-980.

[2] Tu Ya-qing, Zhang Hai-tao, Mao Yu-wen, et al. Unbiased phase delay estimator with negative frequency contribution for real sinusoids[J]. Journal of Applied Sciences, 2013,13(8): 1160-1168.

[3] 杨辉跃, 涂亚庆, 张海涛,等. 一种基于SVD和Hilbert变换的科氏流量计相位差测量方法[J]. 仪器仪表学报, 2012,33(9): 2101-2107.

YANG Hui-yue, TU Ya-qing, ZHANG Hai-tao, et al. Phase difference measuring method based on SVD and Hilbert transform for Coriolis mass flowmeter[J]. Chinese Journal of Scientific Instrument, 2012,33(9): 2101-2107.

[4] 龚国良,鲁华祥. 一种利用固定相移测量同频正弦信号相位差的方法[J].仪器仪表学报,2010,31(4):873-877.

GONG Guo-liang, LU Hua-xiang. Phase difference measurement method of sine signal with same frequency using aptotic phase shifting[J]. Chinese Journal of Scientific Instrument, 2010,31(4):873-877.

[5] 沈廷鳌, 涂亚庆, 李明,等. 基于相关原理的相位差测量改进算法及应用[J].振动与冲击,2014,33(21): 177-182.

SHEN Ting-ao, TU Ya-qing, LI Ming, et al. An improved method for phase difference measurement based on correlation theory[J]. Journal of Vibration and Shock, 2014,33(21): 177-182.

[6] 沈廷鳌, 涂亚庆, 李明,等. 基于多次互相关的非整周期信号相位差测量算法[J]. 仪器仪表学报,2014,35(7): 1578-1585.

SHEN Ting-ao, TU Ya-qing, LI Ming, et al. Research on phase difference measurement algorithm for non-integer period sampling signal based on multi-layer correlation[J]. Chinese Journal of Scientific Instrument, 2014,35(7): 1578-1585.

[7] 李炯,王岩飞. DFT相位估计算法及噪声敏感频率问题分析[J].电子与信息学报,2009,31(9):2101-2103.

LI Jiong, WANG Yan-fei. DFT phase estimation algorithm and noise sensitive frequency region[J]. Journal of Electronics & Information Technology, 2009,31(9): 2101-2103.

[8] Widrow B, Stearns S. Adaptive signal processing[M]. Englewood Cliffs, NJ: Prentice-HaIl, 1985.

[9] 吴慧娟, 文玉梅, 李平. 低信噪比下的LMS自适应无偏时延估计[J]. 电子学报,2009,37(3):500-505.

WU Hui-juan, WEN Yu-mei, LI Ping. Bias-free LMS time delay estimation at low signal-to-noise ratio leves[J]. Acta Electronica Sinica, 2009,37(3):500-505.

[10] Rahmat A H, Mahdi T E. Adaptive filter design based on the LMS algorithm for delay elimination in TCR/FC compensators[J]. ISA Transactions, 2011,50:142-149.

[11] Xia Y L, Danilo P M. A widely linear least mean phase algorithm for adaptive frequency estimation of unbalanced power systems[J]. Electrical Power and Energy Systems, 2014,54:367-375.

[12] 杨辉跃, 涂亚庆, 张海涛,等. 振动信号频率跟踪的反馈修正自适应陷波器法[J].振动与冲击, 2014,33(3):145-149.

YANG Hui-yue, TU Ya-qing, ZHANG Hai-tao, et al. Feedback corrected adaptive notch filter for vibration signal frequency tracking[J].Journal of Vibration and Shock, 2014,33(3):145-149.

[13] 翟春平. 自适应相位差估计器[J]. 舰船科学技术,2011, 33(4):65-68.

ZHAI Chun-ping. Adaptive phase difference estimate[J]. Ship Science and Technology,2011,33(4):65-68.

[14] 罗柏文,万明康, 于宏毅. 两种基于自适应相位补偿的FDOA估计算法[J]. 数据采集与处理,2012,27(1):20-26.

LUO Bai-wen, WAN Ming-kang, Yu Hong-yi. Two algorithms for FDOA estimation based on adaptive phase compensator[J].Journal of Data Acquisition & Processing, 2012,27(1): 20-26.

LMS based phase difference adaptive unbiased estimation method and its application

YANG Hui-yue, TU Ya-qing, ZHANG Hai-tao, LI Ming

(Department of Information Engineering, Logistical Engineering University, Chongqing 401311, China)

Abstract:For phase difference estimation of vibration signals, a LMS based adaptive unbiased estimation method was proposed. In the method, one of the two signals and its orthogonal signal were used to synthesize a new signal which is seen as the estimation of the other signal and the phase difference of the two signals was equal to the ratio of two matching coefficients. The coefficients were adaptively updated to minimize the mean square matching error and then to realize the adaptive estimation of phase difference. The estimation bias resulted from noises was theoretically derived. For improving the precision, the estimated results were compensated according to the estimation bias to obtain an unbiased estimation of phase difference. The compensation formula and process of the proposed method were given out. The experimental results show that the proposed method is able to accurately estimate the phase difference of two signals with the same frequency. The precision of estimation is significantly improved by bias compensation. The proposed method has a good dynamic measurement characteristic which makes it still available when mutations of the phase difference occur. The application of the proposed method in measuring the dynamic phase differences of Coriolis flow meter signals in the varying flow situation verifies its engineering practicability.

Key words:phase difference; adaption; unbiased estimation; LMS algorithm; Hilbert transform

基金项目：国家自然科学基金(61271449；61302175)；重庆市基础与前沿研究计划项目(CSTC2013JCYJA40030; CSTC2015JCYJBX0017)

收稿日期：2015-03-26修改稿收到日期：2015-05-24

通信作者涂亚庆 男，博士,教授,博士生导师，1963年生

中图分类号:TP206+.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.009

第一作者 杨辉跃 男，博士,讲师，1987年生

E-mail:yq.tu@163.com