桥梁工作模态分析中阻尼比识别的离散性研究*

秦世强， 康俊涛， 孔 凡

(1.武汉理工大学道路桥梁与结构工程湖北省重点实验室 武汉，430070) (2.武汉理工大学土木工程与建筑学院 武汉，430070)

桥梁工作模态分析中阻尼比识别的离散性研究*

秦世强1,2， 康俊涛2， 孔 凡2

(1.武汉理工大学道路桥梁与结构工程湖北省重点实验室 武汉，430070) (2.武汉理工大学土木工程与建筑学院 武汉，430070)

准确识别阻尼比一直是桥梁结构模态参数识别的难题。为研究工作模态分析中识别的阻尼比离散性问题，总结了现有的代表性的频域、时域和时频分析的阻尼比识别方法，指出了各种方法导致识别结果不准确的原因。以一个预应力混凝土连续梁桥的工作模态分析为例，分析了阻尼比识别的结果，研究了减小识别的阻尼比离散性的方法。结果表明：相对频率而言，阻尼比识别结果离散程度较高；在混合自由振动响应的情况下，通过增加采样时间，能改善阻尼比识别离散较大的问题，提高识别精度；利用振动水平较低的随机振动响应识别的阻尼比离散性较小。

阻尼比； 模态参数； 半功率带宽； 随机子空间识别； 自由振动响应

引 言

阻尼比是工程结构的基本动力参数之一，直接影响结构的动力行为，因此准确地识别阻尼比有重要的意义。传统方法记录输入输出的模态分析是通过测试结构自由振动响应幅值衰减程度来识别阻尼比。然而，由于激励设备贵重、测试过程复杂，可能会对结构造成损伤，这种方法对大型土木工程结构往往不太实用。大型土木工程结构通常使用环境激励方法，即测试其在风、水流和地脉动等微幅振动下的响应，从而识别其频率、阻尼比和振型。这种方法由于不中断结构的运营，因而又称为工作模态分析(operational modal analysis, 简称OMA)。近年来，对土木工程结构的工作模态分析出现了一系列研究成果[1-5]，得到了广泛认可。相比较频率和振型的识别精度而言，工作模态分析中存在的一个较大问题就是阻尼比难以精确识别[6-8]，多个测试组识别的阻尼比通常呈现较大的离散性，识别结果的可靠性不高。目前，关于这方面研究的文献相对较少。笔者在总结现有一些代表性的阻尼比识别方法的基础上，分析了各种方法中导致阻尼比识别结果离散的原因。通过一个连续梁桥的工作模态分析，进一步分析了阻尼比识别的结果，并研究了提高阻尼比识别精度的方法。

1 半功率带宽法及误差分析

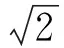
(1)

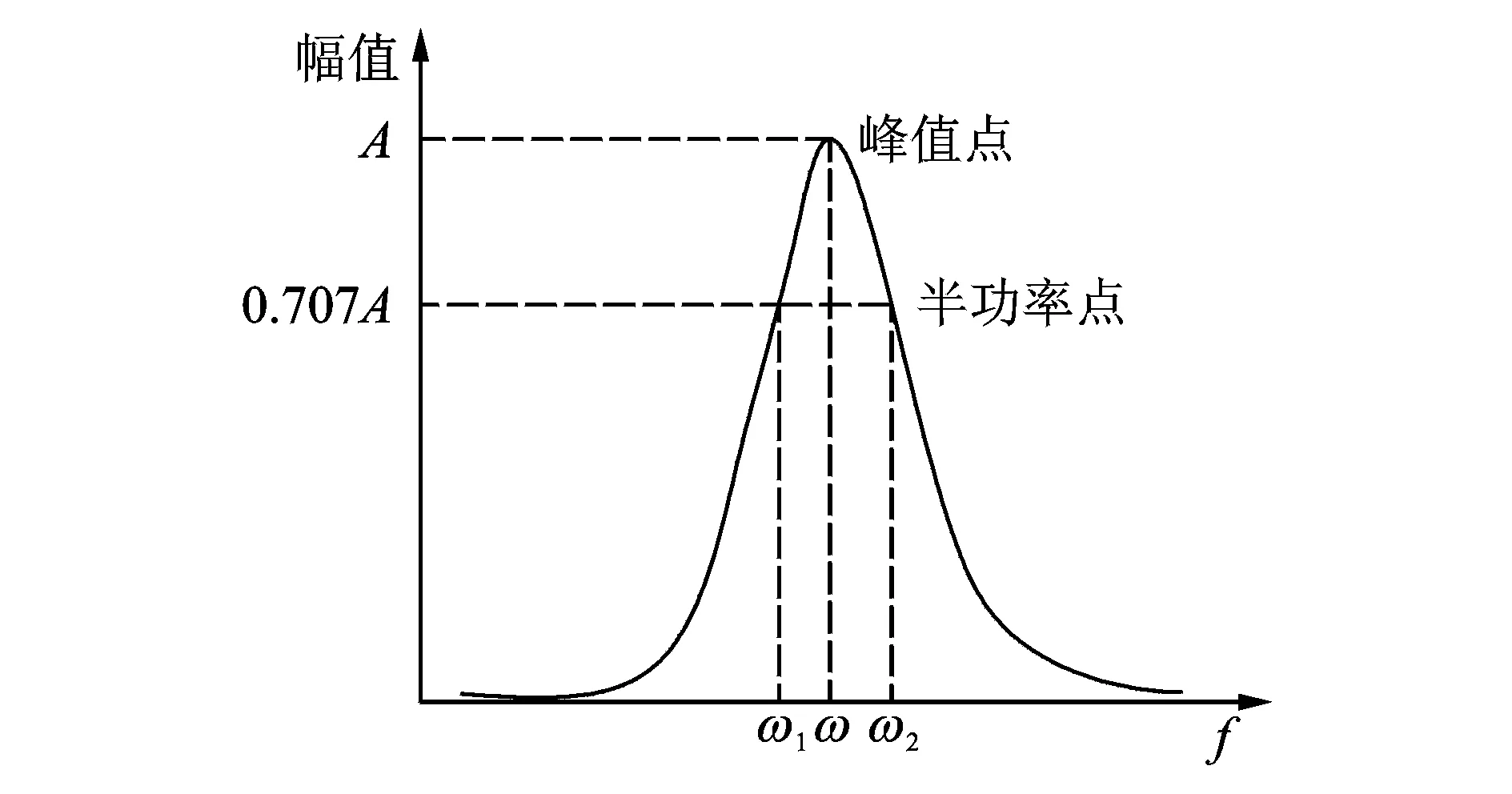
图1 半功率带宽法示意图Fig.1 Schematic diagram of half-power bandwidth method

其中：ω1，ω2分别为半功率带宽点对应的频率值；ω为峰值点对应的频率值。

由于半功率带宽法十分简便，在工程应用中十分广泛。在频响函数精确且频率分辨率较高的情况下，半功率带宽法识别的阻尼比较为精确，一旦峰值频率有较小的误差，阻尼比就会产生较大误差。在工作模态分析中，以下原因会导致半功率带宽法识别的阻尼比结果呈现较大的离散性：a.工作模态分析是利用环境荷载作为激励，激励无法记录，因此无法得到结构的频响函数，一般是用输出响应的自功率谱代替频响函数，这直接导致了阻尼比识别误差；b.多个测试组在人工拾取峰值的过程中会产生人为误差，导致了识别的阻尼比结果离散；c.由于土木工程结构频率呈现低频、模态密集的特点，因而峰值较难准确拾取，这也给半功率带宽法识别阻尼比带来了困难。

2 自由振动响应法及误差分析

通过结构的自由振动响应来计算阻尼比是较为常用的时域阻尼比识别方法。典型的通过直接测试获得结构自由振动响应方法包括力锤试验和突然释放吊重等。此外，也可以利用结构在环境激励下的响应，结合随机减量技术(random decrement technique，简称RDT)和自然激励技术(natural excitation technique, 简称NExT)来获取结构的自由衰减响应[10]。

在获得结构自由振动响应之后，直接根据定义求解阻尼比ξ

(2)

其中：m为振动衰减曲线上量取的波形数；Ai为振动衰减曲线上量取的第i个波形的峰值；Ai+m为振动衰减曲线上量取的第i+m个波形的峰值。

利用定义法识别阻尼比存在的问题包括：a.自由振动响应属于时域响应，其单个时间点的峰值极易受到外界噪声的干扰而产生较大的偏差，因此会导致计算的阻尼比产生较大误差；b.对工作模态分析而言，一般不会直接测试结构自由振动响应，而是利用RDT和NExT方法来获取结构的自由衰减响应，这也导致了一定的误差。

黄方林等[11]提出一种基于自由振动响应的面积法来识别阻尼比，改善了阻尼比识别的精度。如图2所示，自由振动响应时程曲线与时间轴包络形成一系列个面积S1，S3，S5，…以及S2，S4，S6，…；阻尼比可以表达为

(3)

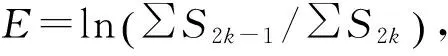
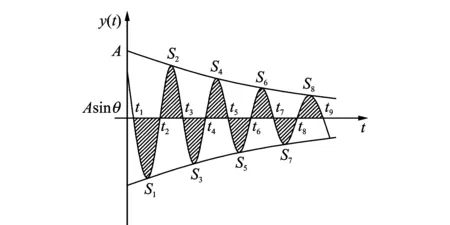
图2 面积法识别阻尼比示意图Fig.2 Schematic diagram of acreage method for damping ratio identification

相比定义法，面积法的正负抵消效应能够平均峰值波动带来的误差，提高阻尼比识别的精度。文献[11]中的数值模拟也表明：随着噪声比例的增加，阻尼比识别的精度也在降低；同时，对于在有噪声干扰的情况下，需要较高的采样频率来保证面积的个数。可见，这种方法也依赖于准确地获得结构自由振动响应。

3 随机子空间识别及误差分析

时域阻尼比识别方法中除了自由振动响应法，还包括最小二乘复频域法[12]、ITD法[13]和随机子空间识别(stochastic subspace identification, 简称SSI)[14]等。时域方法的特点是直接处理测试得到的动力时程曲线数据来进行参数识别。SSI由于其理论体系完备，在识别过程中引入了奇异值分解和卡尔曼滤波等数学工具，便于程序实现且识别结果稳定，因而受到广泛的应用。以数据驱动的SSI(data-driven SSI, 简称SSI-data)为例简要地说明时域方法识别阻尼比的流程。结构随机状态空间模型可以表示为

(4)

其中：yk为测试得到的结构时域响应；xk为结构的状态向量；wk，vk分别为测试误差和结构建模误差；A，C分别为结构的状态矩阵和输出矩阵。

SSI-data的识别过程主要是识别系统矩阵A和C，然后利用特征值分解求解模态参数。利用输出响应构建Hankel矩阵Y0|2i-1

(5)

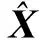
(6)

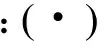
在得到系统的状态矩阵和输出矩阵后，模态参数识别转化为特征值分解问题，对系统状态矩阵A进行特征值分解

(7)

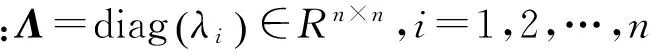
阻尼比ξi可以表示为

(8)

在实际应用过程中，通常取一个较大的系统阶次循环求解模态参数，并将结果绘制在一个以频率为横轴，以系统阶次为纵轴的稳定图上来识别模态参数。尽管SSI在识别频率和模态振型方面已经取得较高精度，但识别的阻尼比仍存在较大离散性。从现有文献看，同一次测试中不同测试组识别的阻尼比的标准差远远高于频率的标准差，这表明在同一测试中不同测试组的结果呈现出较大的离散性，即识别阻尼比存在较高的不确定性。导致SSI阻尼比结果产生误差的原因包括：a.式(4)所示的随机状态空间模型中将环境激励假设为白噪声，而实际中环境荷载并不完全符合这样的假设；b.由连续状态空间转换到离散状态空间带来的误差；c.计算模型误差，如式(5)要求一致性算子j趋近于无穷，实际上就是采样数趋近于无穷，而实际测试中是不可能做到的；d.系统阶次的取值也会影响阻尼比的精度，取值过大，导致较多的数值模态和虚假模态；取值过小，导致结构真实模态无法识别。

4 时频分析法及误差分析

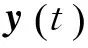
(9)

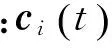
图3 基于HHT的模态参数识别流程Fig.3 The flow chart of modal parameter identification based on HHT

对于基于HHT识别的阻尼比离散的原因包括：a.EMD是一种基于经验的信号处理方法，本身存在一些问题，比如端点飞翼等；b.桥梁固有振动特性一般呈现低频、模态密集的特点，在应用EMD时会出现模态混叠现象，导致本征模态函数不完全是单频率成分；c.利用RDT提取的自由衰减响应与确定的初值和时间段有关系，往往不够理想。

5 工程实例分析

在实际工程中，阻尼比识别结果存在更多的不确定性来源。笔者通过一个预应力混凝土连续梁桥的工作模态分析，对识别的阻尼比结果的离散性进行讨论，并研究提高阻尼比识别精度的方法。

5.1 环境振动测试

该预应力混凝土连续梁桥是高速铁路线路上一座高架桥(图4)，跨径布置为(35+45×4+35) m；截面为箱型截面且沿桥梁纵向梁高一致。为了了解该桥的固有振动特性，对其实施了环境振动测试。采用12个无线传感器测试其在环境荷载下的三向加速度，其中4个传感器布置于参考点进行连续测试，另外8个作为移动测点。传感器布置于箱梁内部底板上(图5)，沿桥梁纵向每隔2.5 m选择一个测试截面，每个截面布置3个测点，总计303个测点。采样频率为200 Hz，每个测试组测试时间约为15 min。现场测试得到典型的加速度响应如图6所示，其幅值约为10-3m/s2。

图4 预应力混凝土连续梁桥Fig.4 The pre-stressed concrete continuous bridge

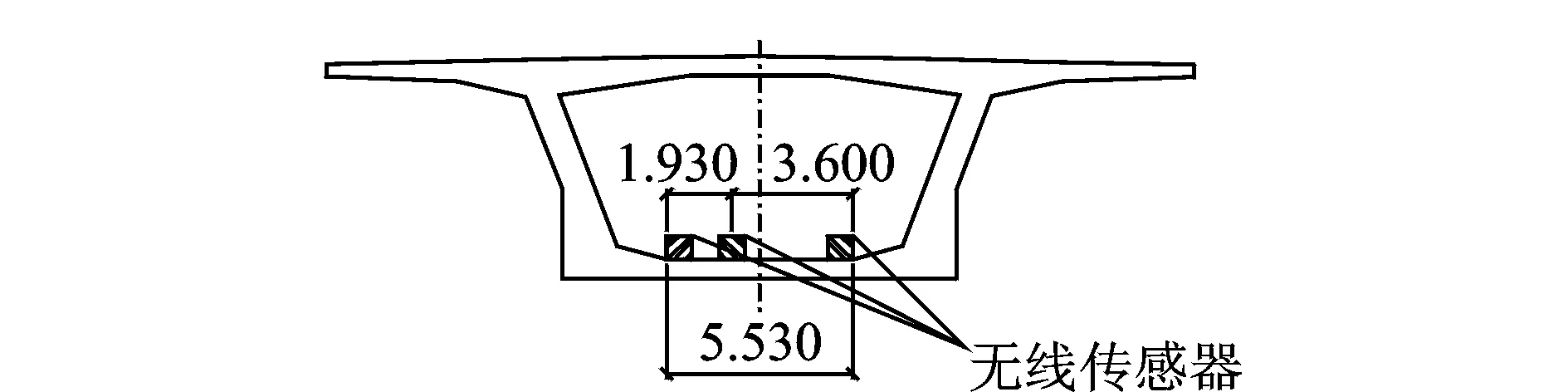
图5 无线传感器在箱梁内布置Fig.5 The layout of wireless sensors in box girder

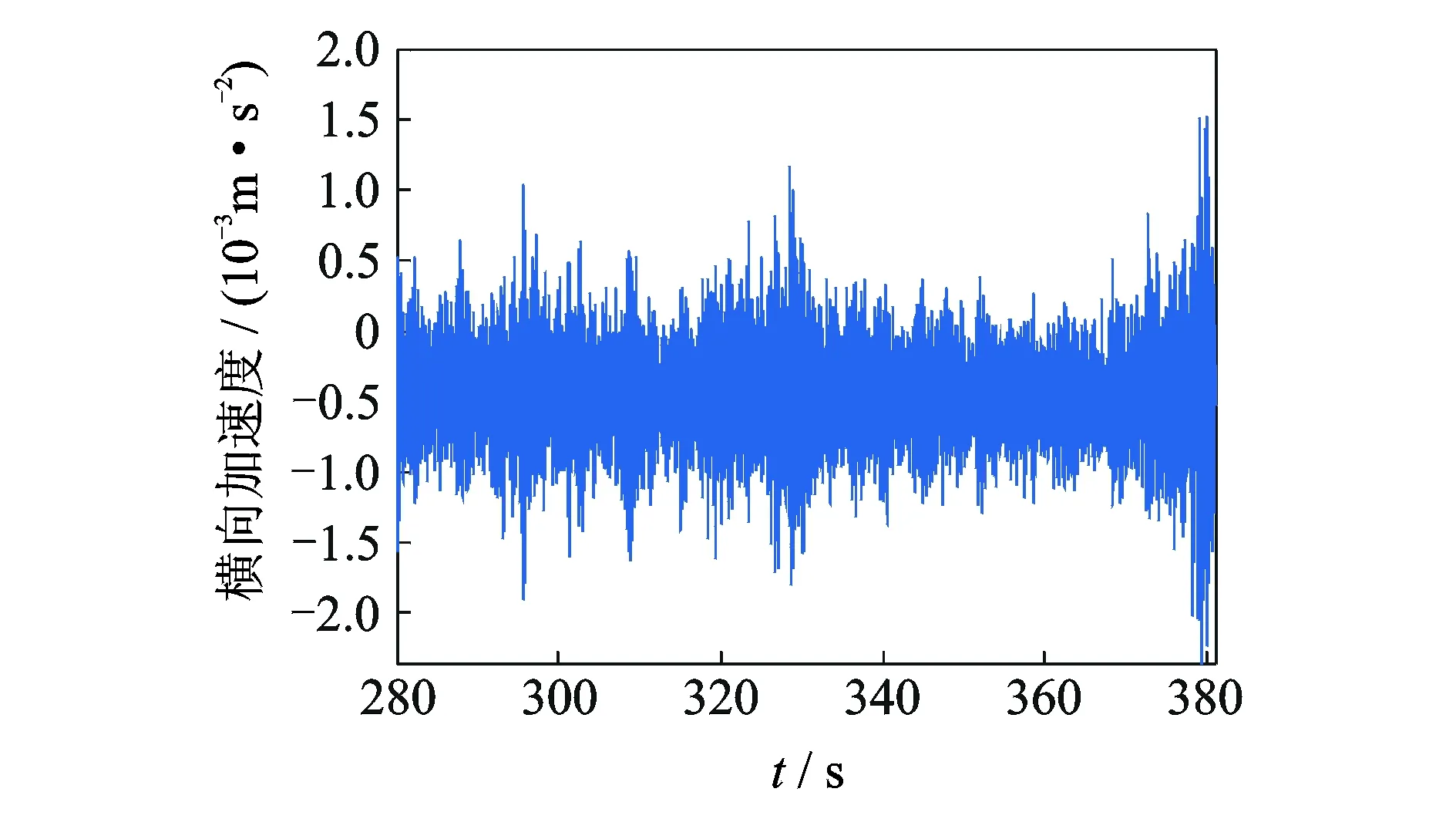
图6 桥梁横向加速度响应Fig.6 The lateral acceleration responses of bridge

5.2 阻尼比识别

图7为该桥测试组2下横向加速度的傅里叶谱。由于是横向加速度，因此只包含横向振动信息。可以看出，峰值带宽较窄，一旦峰值拾取稍微有误差，选择的半功率点就会产生较大误差，从而使得阻尼比识别错误。此外，这里使用加速度响应的傅里叶谱代替结构的频响函数，本身就是一种近似处理手段，其识别的阻尼比产生的误差甚至可以达到100%。图8为利用SSI得到的测试组2的稳定图。稳定图反映了该桥梁的纵向和横向振动信息。稳定轴清晰地显示了桥梁各阶模态信息。如表1所示，将每个测试组识别的桥梁前6阶阻尼比取均值和标准差。为方便对比，列出了频率的均值和标准差。

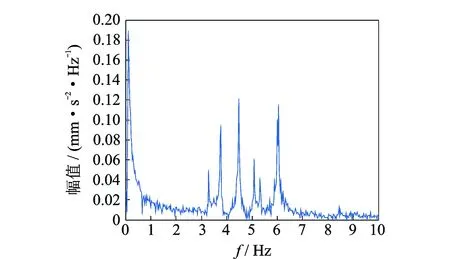
图7 加速度响应的傅里叶谱Fig.7 The FFT spectrum of acceleration response

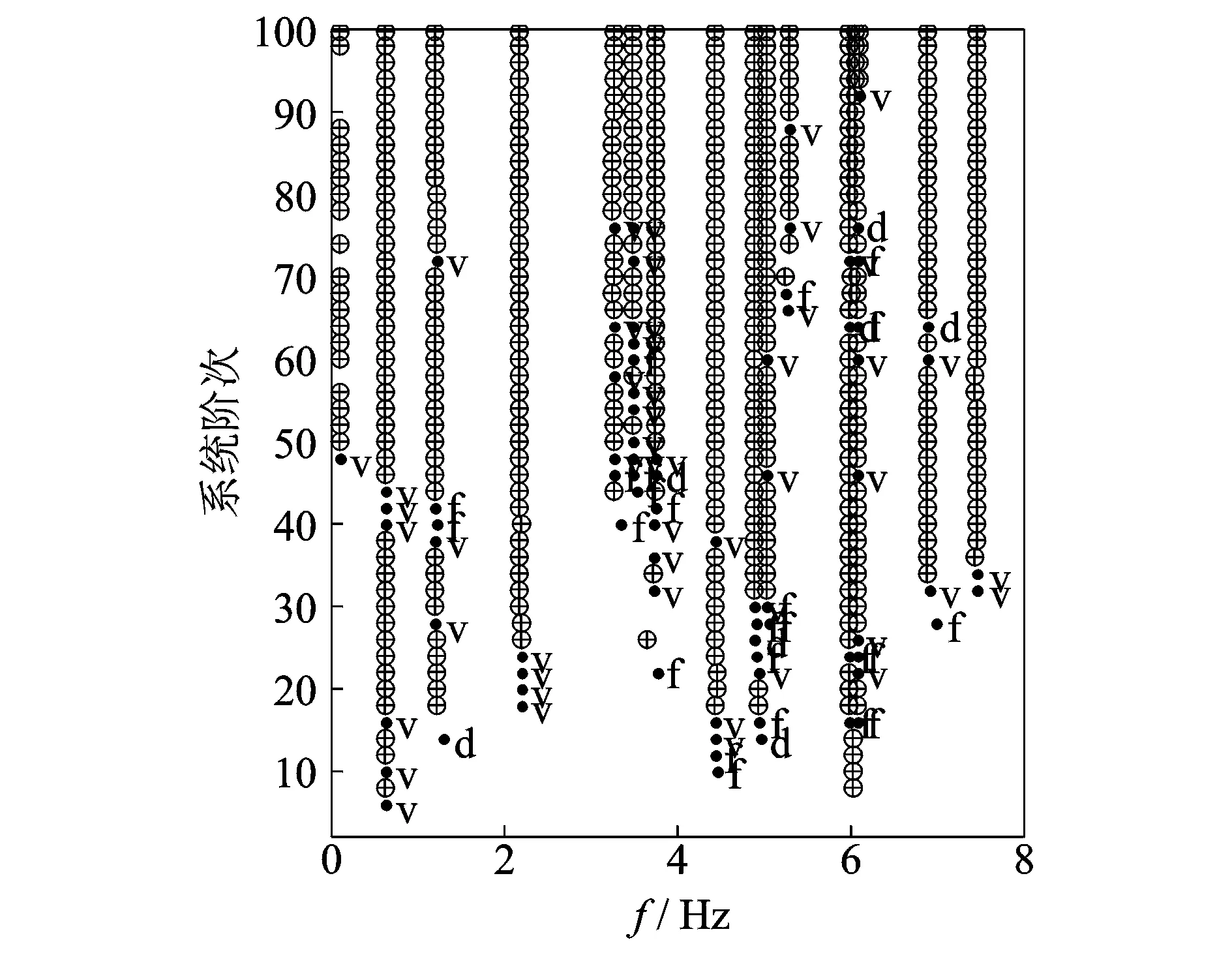
⊕表示频率、阻尼比和振型的共同稳定点；.f，.d和.v分别表示频率、阻尼比和振型的单独稳定点图8 随机子空间识别得到的稳定图Fig.8 The stabilization diagram obtained from SSI

对表1中的数据，首先比较频率和阻尼比结果。桥梁前6阶频率标准差最大为0.012，阻尼比标准差最大为0.65，阻尼比的标准差要远大于频率标准差，这表明识别的阻尼比结果呈现较大的离散性；其次比较阻尼比的均值及标准差，标准差最大约占均值的50%，表明识别的阻尼比本身就存在比较高的不确定性。

表1 多个测试组识别的频率和阻尼比的均值及标准差

Tab.1 The expect values and standard deviations of damping ratios identified from multi-setups

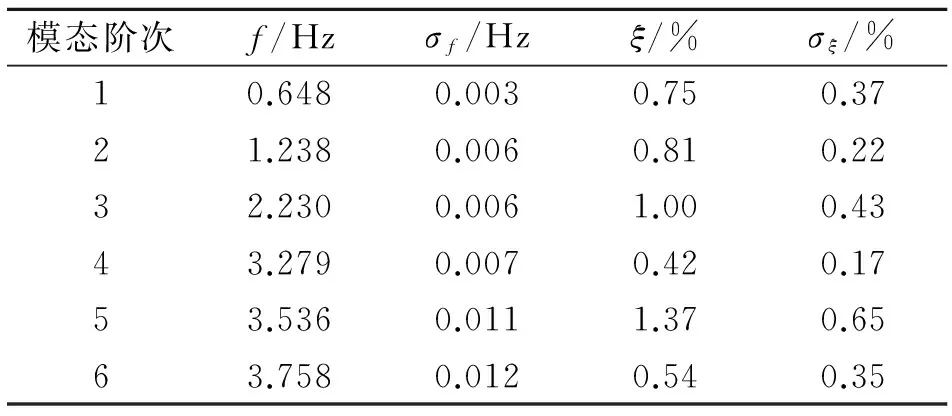
模态阶次f/Hzσf/Hzξ/%σξ/%10.6480.0030.750.3721.2380.0060.810.2232.2300.0061.000.4343.2790.0070.420.1753.5360.0111.370.6563.7580.0120.540.35

5.3 改善阻尼比识别精度

为了改善阻尼比识别离散性较大的问题，研究不同振动水平和不同采样时间对阻尼比识别的影响。如图9所示，数据序列的振动水平是通过考虑桥梁结构在车辆荷载下的自由振动响应实现的；不同采样时间则是通过累加入不同时长的随机振动响应实现。结构动力响应的振动水平可以用响应的均方根值(root mean square,简称RMS)来表示。加速度响应y(t)的RMS值为

(10)

其中：N为y(t)的离散采样数。

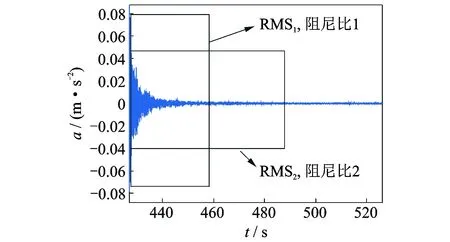
图9 不同振动水平及不同采样时间数据序列示意图Fig.9 Schematic diagram for data sets with different vibration level and sampling time

考虑了自由振动响应混合了10 s，50 s，90 s和200 s时长的随机振动响应4种工况，分别用混合10，混合50，混合90和混合200来表示。以工况混合10为例，说明各工况对桥梁加速度响应截取的原则：从车离桥后的桥梁自由振动响应起始点开始，至自由振动响应幅值衰减至随机振动响应水平为第1个阶段(约6 s)，第2阶段为第1个阶段后延后10 s的纯随机振动响应，两个阶段混合形成工况混合10的加速度响应数据，从而进行阻尼比识别。为了对比，也列入了纯随机振动响应的阻尼比识别结果。需要指出的是，该工况下各测试组时长不同，但最短控制在200 s左右。

表2为前3个测试组下各种工况加速度响应的RMS值。可以看出：a.混合了自由振动响应的RMS值显著提高，表明其信号的振动水平较高；b.随着混合的随机振动响应的时间增加，信号的RMS值在逐渐降低，反映了信号幅值的平均过程；c.RMS值较好地反映了加速度响应的振动水平，即RMS值越大，振动水平越高。这也进一步解释了各种工况数据的区别：振动水平不同、分析时长不同。

表2 不同工况下加速度响应的RMS值

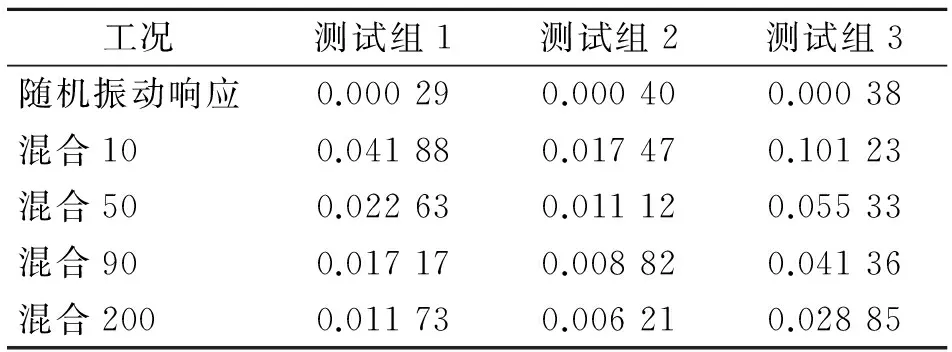
Tab.2 The RMS value of the acceleration response under different conditions m/s2

各工况下多个测试组阻尼比识别的均值和标准差如表3所示，可以看出：a.振动水平较低的随机振动响应识别的阻尼比的标准差较低，而混合了自由振动响应的工况识别的阻尼比标准差相对较高；这表明振动水平较低的随机动力响应识别的阻尼比离散性较小，相对可靠；b.仅看包含自由振动响应的工况，随着采样时间的增长，总体而言识别的阻尼比的标准差在逐渐降低；到工况混合200时，阻尼比的标准差已经接近或低于随机振动响应工况下的结果，这表明通过提高采样时间能够改善阻尼比的识别精度。

从上述研究结果可知，在工程应用中应将测试时段选择在环境荷载振动水平较低时进行，离线分析时利用采样时间较长(采样频率一定的情况下)的随机振动响应识别的阻尼比的离散性最小，识别结果较为稳定。

为了更直观地显示多个测试组在各种工况下阻尼比识别的离散程度，将每个工况下多个测试组识别的阻尼比以散点图的形式绘制于图10中。图中的竖线是随机振动响应工况识别的阻尼比的均值，起参考作用。可以看出，图中有些点是明显超出了桥梁结构阻尼比的范围，是跳点，应不予考虑(表3计算结果中并未考虑跳点，只在图形中直观显示)。除去这些点后，图形直观地反映了各个工况识别的阻尼比的离散程度，随机振动响应工况阻尼比相对聚拢，而混合自由振动响应的工况随着采样时间的增加也逐渐向平均线(图10中竖线)靠拢，基本与表3反映的信息一致。

需要说明的是，这里利用混合自由振动响应与利用强迫振动获取自由振动响应的思路不同。强迫振动获取自由振动响应是传统的测力法进行模态参数识别，而本研究中的混合自由振动响应实际上是考虑了零时刻点结构有一个初始加速度的情况，识别过程在保留工作模态分析的优势同时，来寻求降低阻尼比识别的离散性的方法。

表3 不同工况下识别的阻尼比的均值及标准差

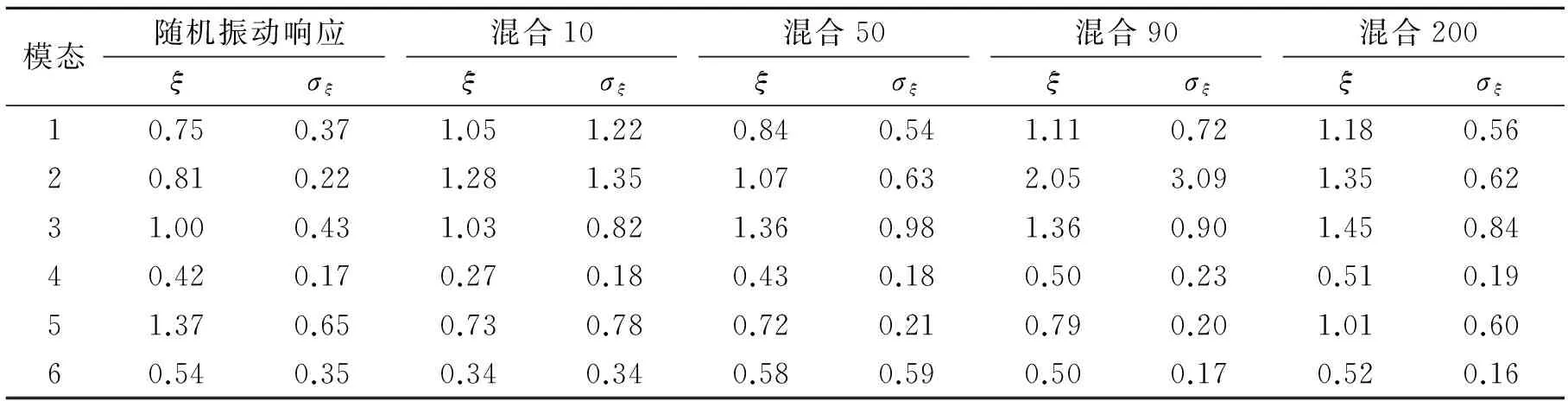
Tab.3 The expect values and standard deviations of damping ratios extracted from different conditions %

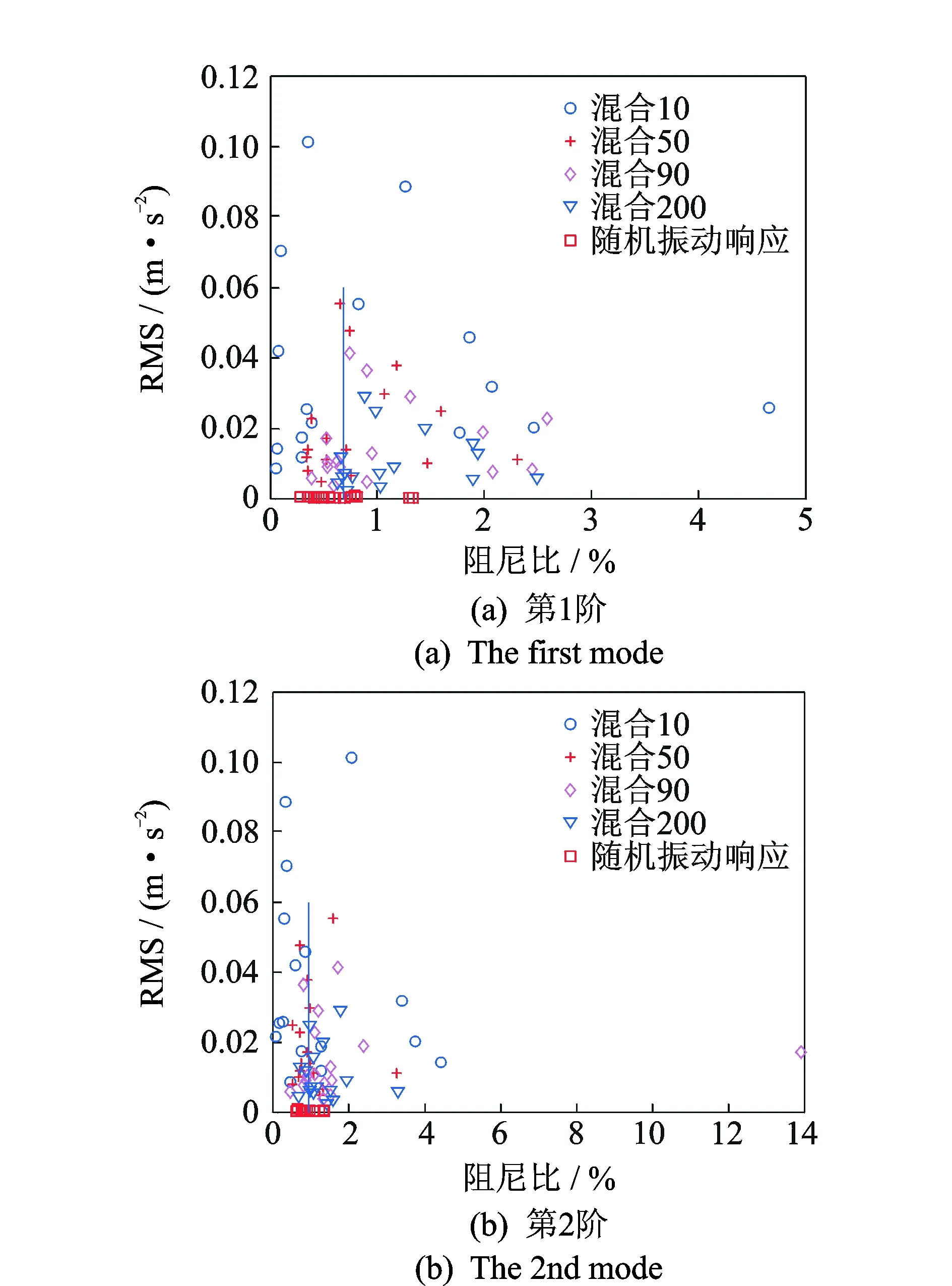
图10 不同工况下多个测试组识别的阻尼比离散图Fig.10 The scatter plot of multi-setups under different conditions

6 结 论

1) 桥梁工作模态分析得到的阻尼比离散程度远高于频率的离散程度，表明识别的阻尼比存在较高的不确定性和随机性。

2) 对同样的测试数据，各种阻尼比识别方法都存在识别阻尼比离散性较大的现象，说明目前对桥梁结构的阻尼机理不明确。

3) 在混合自由振动响应的情况下(即考虑桥梁结构在零时刻点的加速度不为0)，通过增加采样时间能够减小各测试组的识别的阻尼比标准差，得到更为稳定的结果。

4) 相对而言，利用长时间低振动水平的随机振动响应识别的阻尼比标准差最小，结果稳定。

[1] Magalhaes F, Cunha A. Explaining operational modal analysis with data from an arch bridge[J]. Mechanical System and Signal Processing, 2011, 25(5): 1431-1450.

[2] Peeters B, De Roeck G. Reference-based stochastic subspace identification for output-only modal analysis[J]. Mechanical Systems and Signal Processing, 1999, 13(6): 855-878.

[3] Reynders E. System identification methods for (operational) modal analysis: review and comparison[J]. Archives of Computational Methods in Engineering, 2012, 19(1): 1-74.

[4] 林贤坤, 覃柏英, 张令弥, 等. 基于附加质量的试验模态振型质量归一化[J]. 振动、测试与诊断, 2012,32(5):784-790.

Lin Xiankun, Qin Boying, Zhang Lingmi, et al. Way of getting mass-normalized experimental mode shapes based on mass changes[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5):784-790. (in Chinese).

[5] 刘宗政, 陈恳, 郭隆德, 等. 基于环境激励的桥梁模态参数识别[J]. 振动、测试与诊断, 2010,30(3):300-303.

Liu Zongzheng, Chen Ken, Guo Longde, et al. Modal parameter identification of a bridge under ambient excitation[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(3):300-303. (in Chinese)

[6] Magalhaes F, Cunha A, Caetano E, et al. Damping estimation using free decays and ambient vibration tests[J]. Mechanical System and Signal Processing, 2010, 24(5): 1274-1290.

[7] Torvik P J. On estimating system damping from frequency response bandwidths[J]. Journal of Sound and Vibration, 2011, 330(25): 6088-6097.

[8] 陈隽，徐幼麟，李杰. Hilbert-Huang变换在密频结构阻尼识别中的应用[J]. 地震工程与工程振动, 2003, 23(4): 34-42.

Chen Jun, Xu Youlin, Li Jie. Hilbert-Huang transform for damping ratio identification of structures with closely spaced modes of vibration[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(4): 34-42. (in Chinese)

[9] 应怀樵，刘进明，沈松. 半功率带宽法与INV阻尼计法求阻尼比的研究[J]. 噪声与振动控制, 2006(2): 4-6.

Ying Huaiqiao, Liu Jinming, Shen Song. Half-power bandwidth method and INV damping ratio solver study[J]. Noise and Vibration Control, 2006(2): 4-6. (in Chinese)

[10]韩建平，李达文. 基于Hilbert-Huang变换和自然激励技术的模态参数识别[J]. 工程力学, 2010，27(8): 54-59.

Han Jianping, Li Dawen. Modal parameter identification based on Hilbert-Huang transform and natural excitation technique[J]. Engineering Mechanics, 2010, 27(8): 54-59. (in Chinese)

[11]黄方林，何旭辉，陈政清，等. 识别结构模态阻尼比的一种新方法[J]. 土木工程学报, 2002, 35(6): 20-23.

Huang Fanglin, He Xuhui, Chen Zhengqing, et al. A new approach for identification of modal damping ratios for a structure[J]. Chinese Journal of Civil Engineering, 2002，35(6): 20-23. (in Chinese)

[12]孙鑫晖，郝木明，张令弥. 环境激励下宽频带模态参数识别研究[J]. 建筑结构学报, 2011，32(4): 151-156.

Sun Xinhui, Hao Muming, Zhang Lingmi. Research on broadband modal parameters identification under ambient excitation[J]. Journal of Building Structures, 2011, 32(4): 151-156. (in Chinese)

[13]Mohanty P, Rixen D J. A modified Ibrahim time domain algorithm for operational modal analysis including harmonic excitation[J]. Journal of Sound and Vibration, 2004, 275(2): 375-390.

[14]Overschee P, De Moor B. Subspace identification for the linear systems: theory-implementation-applications[M]. Boston: Kluwer Academic Publishers, 1996:57-69.

[15]朱宏平，翁顺. 运用小波分析方法进行结构模态参数识别[J]. 振动与冲击, 2007，26(4): 1-4.

Zhu Hongping, Weng Shun. Identification of structural modal parameters with wavelet transformation[J]. Journal of Vibration and Shock, 2007, 26(4): 1-4. (in Chinese)

[16]闵志华，孙利民，孙智，等. 环境激励下基于小波变换和奇异值分解的结构模态参数识别[J]. 振动工程学报, 2009, 22(2): 142-149.

Min Zhihua, Sun Limin, Sun Zhi, et al. Structural modal parameter identification using wavelet transform and singular value decomposition under ambient excitation[J]. Journal of Vibration Engineering, 2009, 22(2): 142-149. (in Chinese)

[17]王学敏. 基于Hilbert-Huang变换的桥梁监测信号分析与处理和时变模态参数识别[D]. 长沙：中南大学, 2008.

10.16450/j.cnki.issn.1004-6801.2016.01.007

*国家自然科学基金资助项目(51108382)；道路桥梁与结构工程湖北省重点实验室开放基金资助项目(DQJJ201308)；中央高校基本科研业务费专项资金资助项目(2014-IV-047)

2014-01-08；修回日期：2014-04-02

TU311; TH113

秦世强，男，1987年7月生，博士、讲师。主要研究方向为桥梁健康监测、结构动力学系统识别。曾发表《Effects of initial conditions in operational modal analysis》(《Structural Control and Health Monitoring》2014, No.21)等论文。 E-mail：qsqiang417@gmail.com