振动环境下插装阀的动态特性*

杨忠炯， 周振峰， 周立强

(1.中南大学高性能复杂制造国家重点实验室 长沙，410083) (2.中南大学机电工程学院 长沙，410083)

振动环境下插装阀的动态特性*

杨忠炯1，2， 周振峰2， 周立强1，2

(1.中南大学高性能复杂制造国家重点实验室 长沙，410083) (2.中南大学机电工程学院 长沙，410083)

为研究强振动环境对二通插装阀工作性能的影响，建立了振动环境下的二通插装阀结构模型及AMESim仿真模型,分别分析振动条件及插装阀结构参数对其动态特性的影响规律。研究表明：基础振动会引起插装阀阀口流量及阀芯开度出现波动现象；阀芯在稳态时的波动程度随基础振动幅值线性增加，振动频率大于20Hz后，波动程度明显。较小的阻尼孔径会使流量上升至最大值的时间增加，但通过阀口的流量更平稳；插装阀在开启状态时，阀芯波动值与阀芯质量呈正相关关系；改变插装阀的面积对改善流量波动现象效果有限；增加弹簧刚度可以改善流量波动现象，但会使通过阀口的流量减小。

基础振动； 插装阀； 动态特性； 振动条件； 结构参数

引 言

二通插装阀具有流通能力大、动作快和密封性能好等特点，在高压大流量领域应用比较广泛[1]。全断面硬岩掘进机(tunnel boring machine，简称为TBM)液压系统具有大负载、大功率和大流量等特点，因此TBM上广泛采用大规格的二通插装阀[2]。例如：美国ROBBINS公司的MB264-311型TBM支撑、推进液压系统共使用了16个二通插装阀[3]；德国WIRTH公司的TB880E型TBM支撑系统使用了2个二通插装阀来保证差动快进[4]。

重大工程装备在工作时会不可避免地产生振动现象[5]，基础振动会对插装阀的工作特性造成一定影响，目前对插装阀的工作特性研究主要集中在阀体结构和流体动力学等方面。李淮祥[6]分析了插装阀锥角和阀芯圆周直径的大小对锥阀振动特性和静态特性的影响。文献[7]分析了锥阀入口速度、出口速度、阀口开启度和锥角对空化效应的影响。文献[8]对不同开口度的阀隙流速进行仿真，得出了锥阀阀隙处压力损失与开口度大小的关系。文献[9]研究了插装阀液压系统中蓄能器的振动衰减影响，对锥阀的稳定性进行了分析。目前，部分学者对模拟强振动环境的试验台进行了研究。张志等[10]对振动试验台的加速度积分方法进行了探究。黄中华等[11]对振动试验台的测控系统进行了研究。由于针对插装阀在振动试验台上的性能研究较少，因此研究基础振动下的插装阀工作特性具有重要意义。

1 基础振动下的插装阀模型

典型的二通插装阀由先导阀、控制盖板和插装件3部分构成。插装件由阀芯、阀套、弹簧和密封圈等组成[12]。先导阀、控制盖板、阀套与阀块采用螺钉紧固，可作为一个刚性连接的整体。振动条件下的二通插装阀结构模型如图1所示。X1为基础振动位移，X2为阀芯运动位移，取向上的位移方向为正。阀芯开启时开启高度以X表示，X=X2-X1。

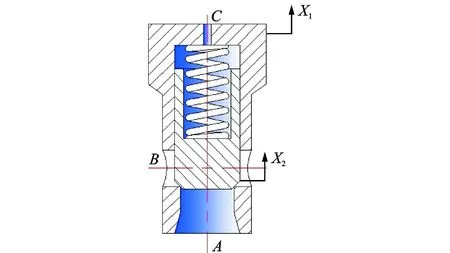
图1 振动条件下的插装阀结构模型Fig.1 Cartridge valve structure model under vibration condition

在TBM的主机支撑系统中[4]截取一个简单的二通插装阀换向回路作为研究对象，如图2所示。先导电磁阀不得电时，插装阀入口处A腔压力Pa与控制腔C腔压力Pc相等，C腔承压面积大，此时插装阀关闭。先导电磁阀得电时，控制腔C腔油液回油箱，压力Pc减小，在压差及弹簧力的共同作用下，插装阀阀芯打开，油液从A腔流向B腔。

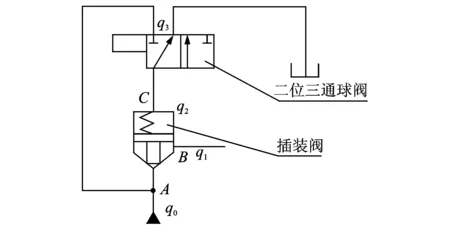
图2 插装阀简单换向回路Fig.2 Simple cartridge valve commutation circuit

2 系统数学模型

设系统泵源流量为q0，插装阀阀口流量为q1，插装阀阀芯运动导致控制腔体积变化引起的流量为q2，二位三通球阀的流量方程为q3。进油口A腔、出油口B腔、控制腔C腔的压力分别以Pa，Pb，Pc表示，进油口A腔、出油口B腔、控制腔C腔的液压作用面积分别以Aa，Ab，Ac表示。

插装阀阀口的压力-流量方程为

(1)

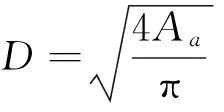
先导阀二位三通球阀的压力-流量方程为

(2)

其中：C为流量系数，约为0.62～0.75[13]；d为先导电磁阀过流孔径。

插装阀控制腔体积变化引起的流量为

(3)

其中：Vc为C腔的体积；E为油液体积弹性模量。

插装阀控制腔的流量连续方程为

(4)

插装阀阀口的流量连续性方程为

(5)

假定基础处于简谐振动环境，X1=Asinωt，取向上的位移为正。忽略阀芯与阀套间的动摩擦力与阀芯重力的影响，当阀芯开启时，根据外部激励作用下的强迫振动理论[14]，插装阀阀芯运动微分方程为

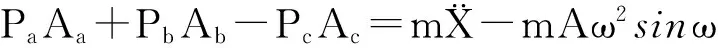
(6)

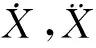
插装阀所受稳态液动力与其过流面积、阀口压差有关，总是使插装阀阀芯趋于关闭，其方程[15]为

Fw=-CwπDXΔPsin2α

(7)

其中：Cw为流量系数，约为0.77～0.82。

3 系统仿真及分析

根据数学模型方程，利用AMESim仿真软件建立其仿真模型，如图3所示。仿真系统中主要元件参数设置为：泵源排量为300ml/r，转速为1 200r/min，溢流阀设定压力为10MPa，其他模型参数如表1所示。插装阀阀芯最大开启高度为10mm，控制腔回油路阻尼孔径为3mm，弹簧刚度为1.6×105N/m，插装阀结构参数如表2所示。

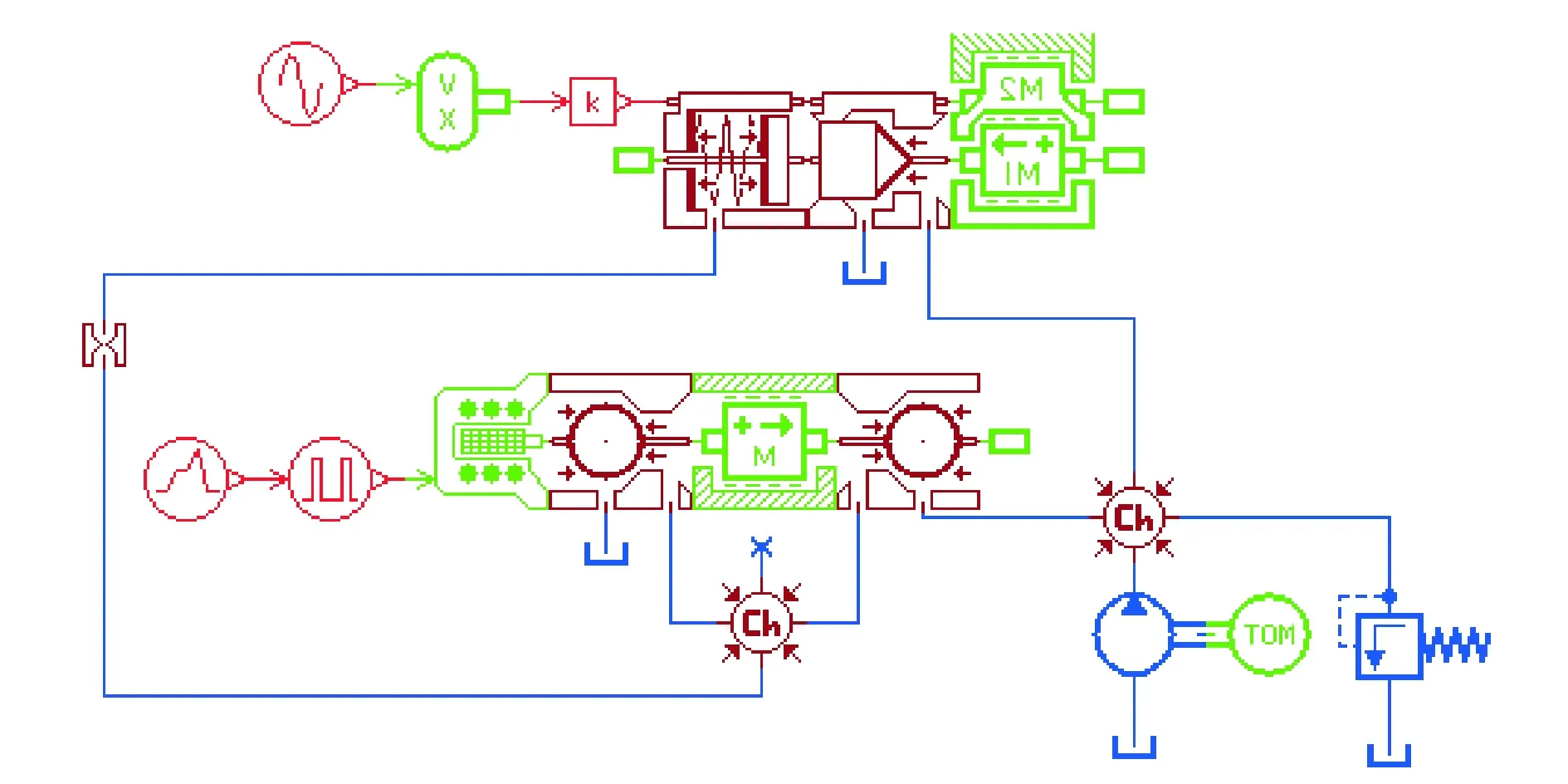
图3 振动下的插装阀仿真模型Fig.3 Cartridge valve simulation model under vibration

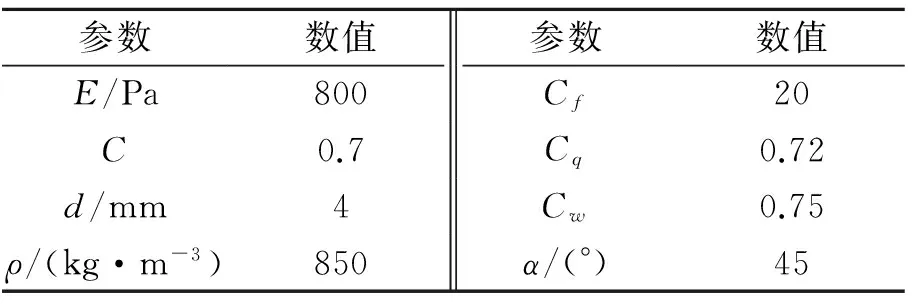
参数数值参数数值E/Pa800Cf20C0.7Cq0.72d/mm4Cw0.75ρ/(kg·m-3)850α/(°)45

表2 插装阀主要结构参数表

在振动条件为振幅A为0.005 m，频率为100 Hz时，插装阀阀口流量的仿真结果如图4所示。由仿真结果可以得出， 基础振动对插装阀阀口流量的影响主要在于其达到平衡阶段后会出现周期性波动现象。由式(1)可知，在压力不变的情况下，插装阀开启高度是决定阀口流量的重要因素。

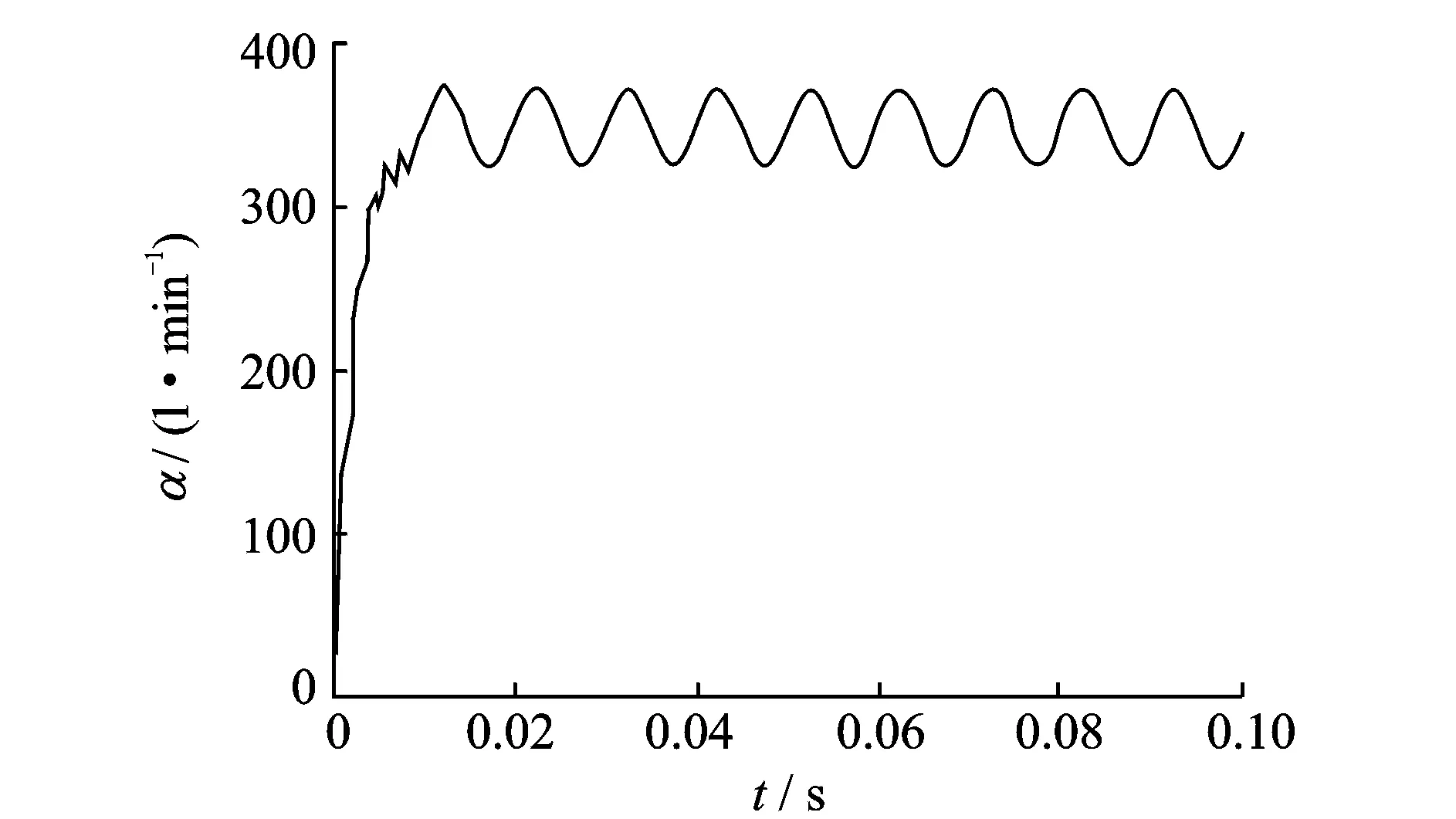
图4 插装阀流量仿真结果Fig.4 Simulation results of cartridge valve flow

3.1 基础振动对阀芯开启的影响规律

在插装阀受到基础振动(振幅A为0.005 m，频率为100 Hz)与无振动时，阀芯开启高度X的仿真结果如图5所示。由图5可知，在阀芯开启时，基础振动对其快速上升阶段影响不大， 这是因为阀芯快速上升时，由于控制腔C腔压力迅速减小，进油口A腔作用力远大于基础振动造成的阀芯惯性力，所以阀芯迅速打开。在阀芯处于动态平衡阶段时，基础振动会导致阀芯出现波动现象。这是当阀芯在液

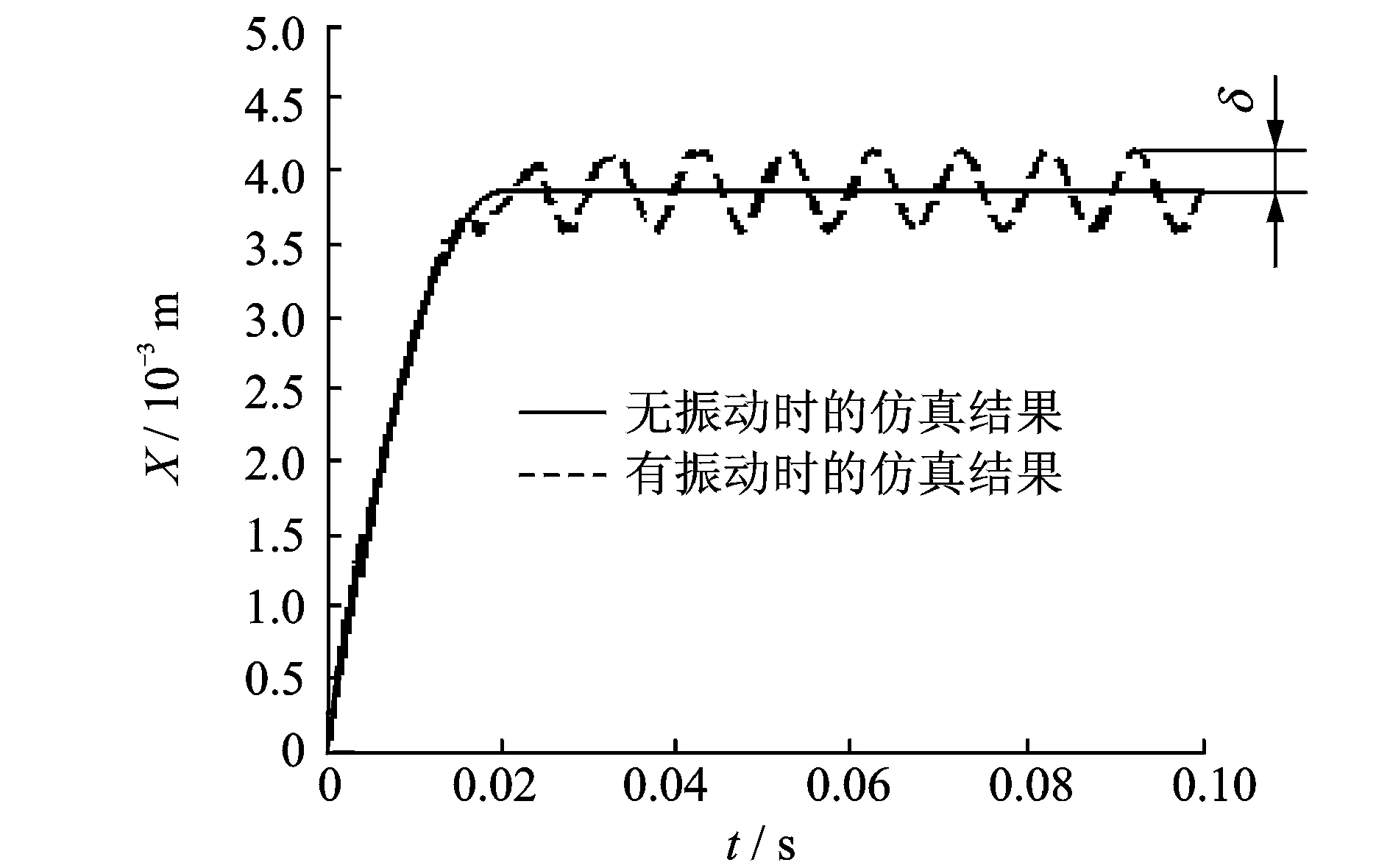
图5 基础振动下的X仿真结果Fig.5 Simulation results of X under fundamental vibration

压作用力、弹簧力和稳态液动力作用下到达平衡状态时，基础振动造成的阀芯惯性力周期性变化，打破了阀芯的受力平衡，阀芯开启高度也出现周期性变化规律。设定阀芯周期波动的幅值为δ，设定无振动时阀芯的开启高度为X0，可用δ/X0的比值来反映阀芯开启高度受基础振动的影响程度。

3.1.1 基础振动幅值A的影响

为研究基础振动幅值A对阀芯开启时的影响规律，设立3组仿真试验。由中国铁建重工集团在越南工地的测试报告显示，TBM左侧撑靴振动频率主要集中在100 Hz以内，故仿真试验频率分别取f为80，60和30 Hz。记录阀芯周期波动幅值δ与稳态平衡值X0的仿真结果，δ/X0的比值如图6所示。可见，阀芯在稳态平衡时的波动比值δ/X0随基础振动幅值A的增加而线性增加。

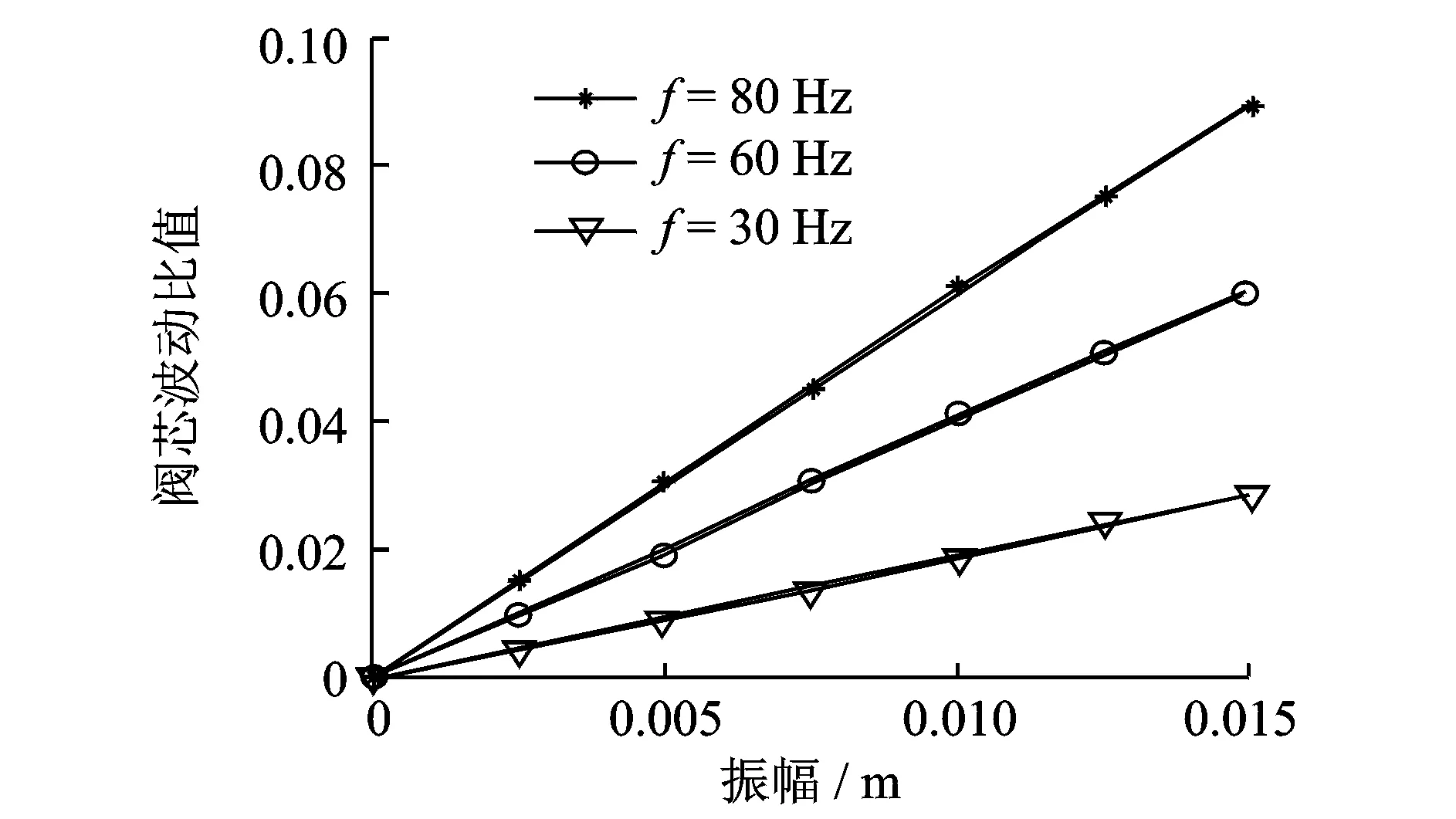
图6 δ/X0比值随振幅变化曲线Fig.6 Curves of δ/X0 ratio changing with amplitude

3.1.2 基础振动频率f的影响

为研究基础振动频率f对阀芯开启时的影响规律，同样设立3组仿真试验，振动幅值分别为A=0.01 m，A=0.007 5 m，A=0.005 m，δ/X0的比值如图7所示。由图7可知，当基础振动频率增加时，阀芯在稳态波动时的比值首先会缓慢增加，这是因为振动频率较小时阀芯所受惯性力数值不大，对阀芯平衡影响不大；当振动频率超过20 Hz时，阀芯波动比值才急剧增加。

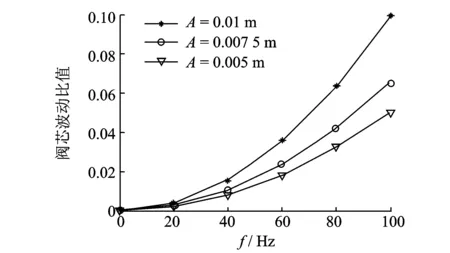
图7 δ/X0比值随频率变化曲线Fig.7 Curves of δ/X0 ratio changing with frequency

3.2 阀体结构对动态特性的影响规律

3.2.1 阻尼孔径的影响

为研究控制腔C腔与先导阀之间的阻尼塞孔径对插装阀动态特性的影响规律，在阻尼塞孔径可选规格中分别选择Φ为1.5，2和3 mm 3组进行仿真试验，修改图3所示模型中的阻尼孔直径，插装阀流量仿真结果如图8所示。控制腔C腔的压力变化如图9所示。由图8可知，当阻尼孔径变大时，插装阀阀口流量达到最大值所需时间减小且流量波动幅度增加。这是由于阻尼孔径增加后，阻尼孔的流通能力增加，控制腔C腔的压力下降时间减小；同时控制腔的体积变化率加大，导致插装阀阀芯波动值变大，进一步引起流量波动值变大。

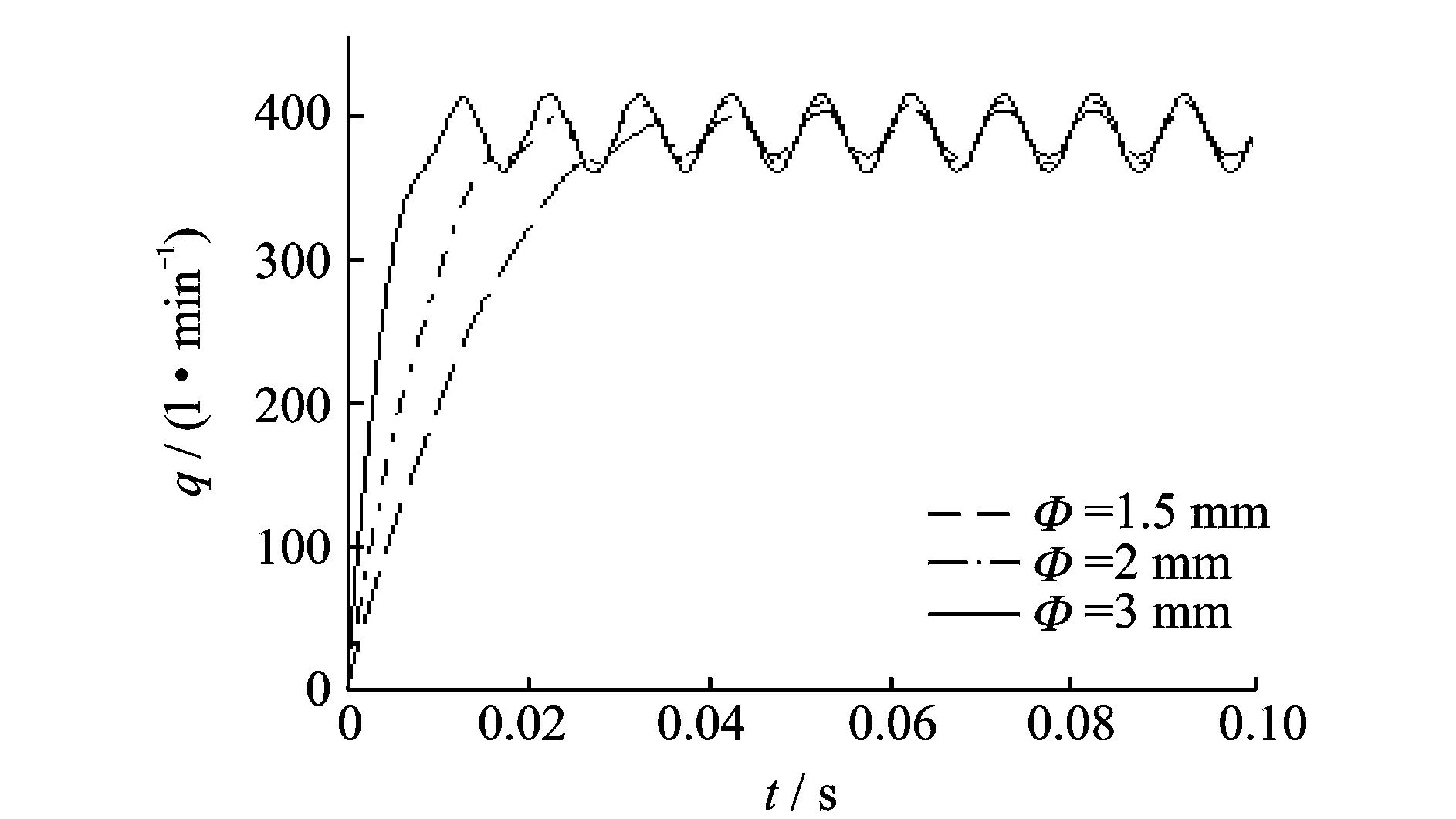
图8 插装阀阀口流量Fig.8 The outlet flow of cartridge valve

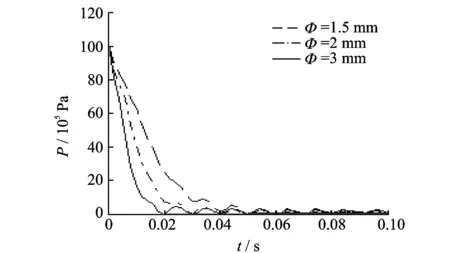
图9 控制腔压力变化曲线Fig.9 Pressure variation curves of controlled chamber

3.2.2 阀芯质量对阀芯稳态平衡的影响

设阀芯质量分别为m=0.125 kg，m=0.1 kg和m=0.075 kg的3组仿真试验，阀芯开启高度X在稳态平衡后的仿真结果如图10所示。由图10可知，插装阀阀芯在稳态平衡阶段的波动值与插装阀的质量呈正相关性，质量越大，其波动值亦越大。

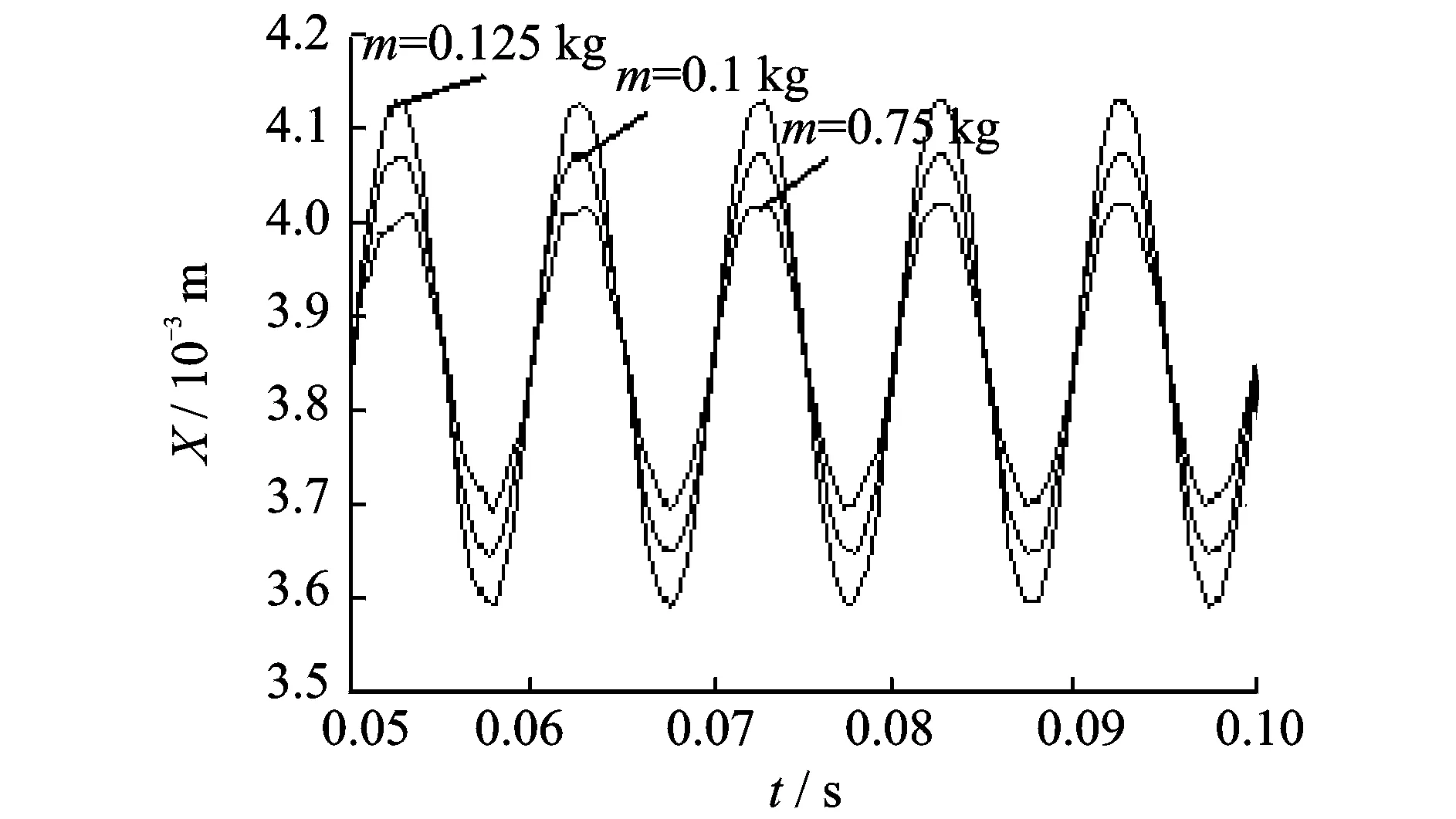
图10 不同阀芯质量下的X仿真结果Fig.10 Simulation results of X under different spool mass

3.2.3 面积比的影响

插装阀进油口A腔面积与控制腔C腔面积比值Aa/Ac称为其面积比，常见的面积比有1∶1.07，1∶1.5，1∶2.0几种，根据上述3种面积比进行仿真试验，插装阀阀口流量仿真结果如图11所示。由图11可知，插装阀流量值随面积比的减小而显著减小，而到达流量最大值的时间及波动幅值并无太大差异，这是因为面积Aa的减小造成插装阀阀口的过流面积减小，阀口流量必然随之减小。

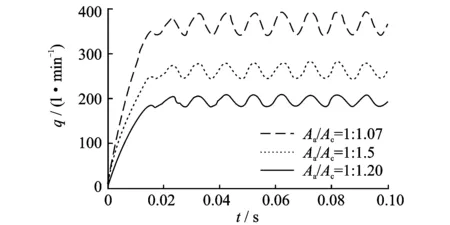
图11 不同面积比的流量仿真结果Fig.11 Simulation results of flow under different area ratio

3.2.4 弹簧刚度的影响

取弹簧刚度分别为1.2×105，1.6×105和2.0×105N/m进行仿真试验，阀芯达到稳态平衡后的仿真结果如图12所示。由图12可知，随着弹簧刚度的增加，插装阀阀芯波动值会减小，其开启高度也减小，因此增加弹簧刚度能减弱阀芯波动程度，但同时会使通过其阀口的流量减小。

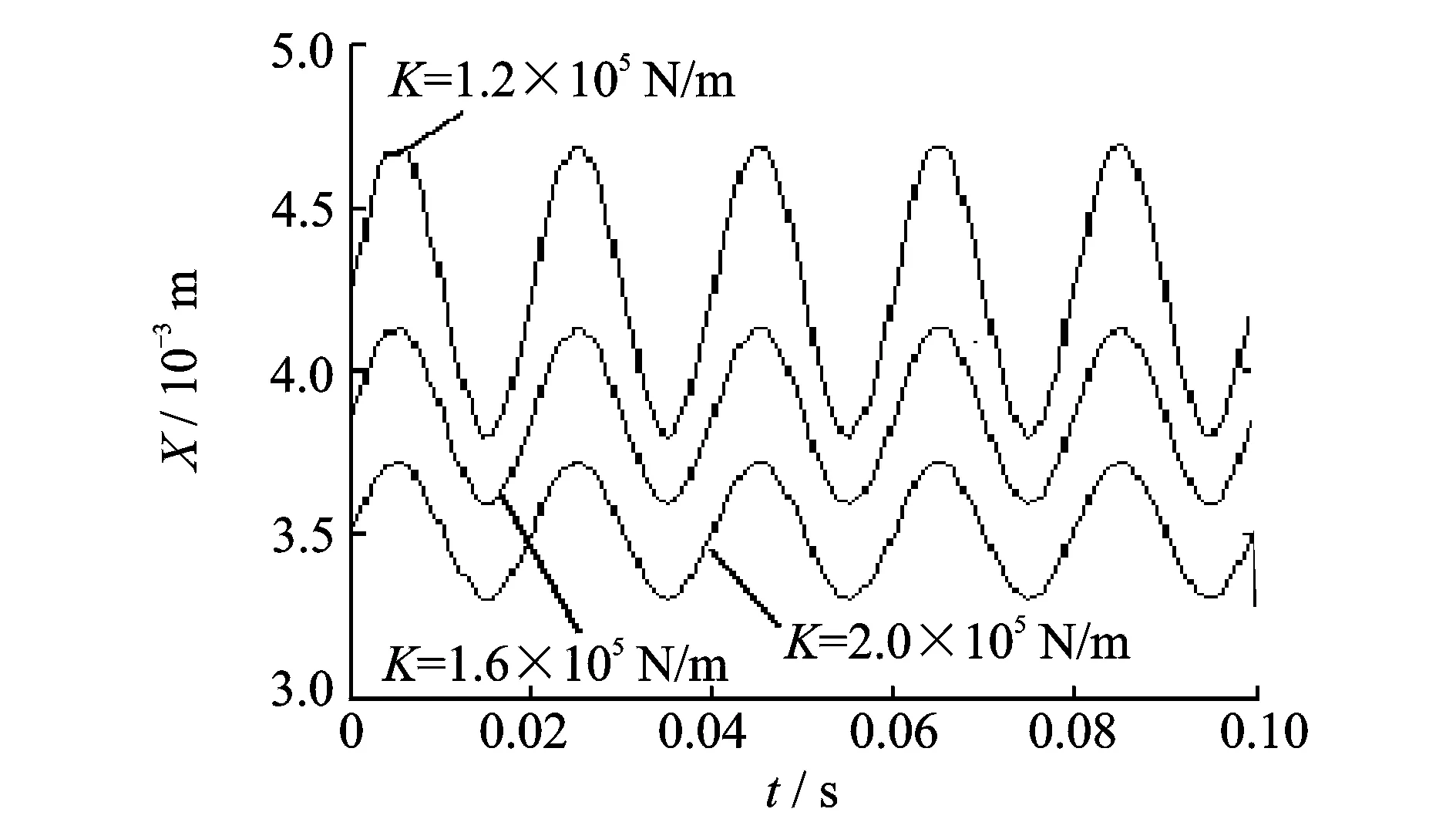
图12 不同弹簧刚度下的X仿真结果Fig.12 Simulation results of X under different spring stiffness

4 结 论

1) 基础振动对插装阀开启时的影响主要体现是：阀芯在平衡阶段会出现周期性波动现象，阀口流量值不稳定。

2) 阀芯在稳态时的波动比值δ/X0随基础振动幅值A线性增加；只有振动频率超过20Hz，阀芯波动比值δ/X0才随振动频率的增加而急剧增加。

3) 在振动环境下，选择较小的阻尼孔径和较小的阀芯质量可以改善阀口流量波动现象；在保证流量足够的前提下应尽量选择刚度较大的弹簧。

[1] 毛卫平.液压阀[M].北京：化学工业出版社，2009:144-146.

[2] 黄人豪. 二通插装阀和比例控制技术在中国重大工程和装备中的应用[J]. 流体传动与控制，2004(1)：24-30.

Huang Renhao. Applications of hydraulic catridge valve and proportional control technology[J].Fluid Power Transmission and Control, 2004(1)：24-30.(in Chinese)

[3] 杜彦良，杜立杰.全断面岩石隧道掘进机—系统原理与集成设计[M].武汉：华中科技大学出版社，2010: 119-124.

[4] 周赛群.全断面硬岩掘进机(TBM)驱动系统的研究[D].杭州：浙江大学，2008.

[5] Zhang Kuan，Yu Hai，Liu Zhi，et al. Dynamic characteristic analysis of TBM tunneling in mixed-face conditions [J]. Simulation Modelling Practice and Theory，2010，18(7)：1019-1031.

[6] 李淮祥.液压锥阀的振动特性研究[D].成都：西南交通大学，2012.

[7] Gao Hong,Fu Xin,Yang Huaiyong, et al. Numerical investigation of cavitating flow behind the cone of a poppet valve in water hydraulic system[J]. Journal of Zhejiang University,2002,3 (4):395-400.

[8] 何卫卫，刘浩辉，宋金朋.水压锥阀流场的CFD计算与分析[J]．机械管理开发，2010，25(3)：34-37．

He Weiwei,Liu Haohui,Song Jinpeng. Analysis and CFD simulation of the flow field in water hydraulics poppet valve[J]．Mechanical Management and Development,2010,25(3):34-37.(in Chinese)

[9] Li Zhongfu. Effects of accumulator on stabilization of direct acting poppet valve and its system[J]. Journal of China University of Mining & Technology,1998,8 (1):80-83.

[10]张志，孟少平，周臻，等. 振动台试验加速度积分方法[J].振动、测试与诊断，2013，33(4)：627-633.

Zhang Zhi, Meng Shaoping, Zhou Zhen, et al. Numerical integration method of acceleration recodes for shaking table test[J]. Journal of Vibration, Measurent & Diagnosis, 2013，33(4)：627-633.(in Chinese)

[11]黄中华，刘质，胡琼,等.工程机械混合动力系统实验台测控系统[J]. 振动、测试与诊断，2013，33(1)：144-148.

Hang Zhonghua, Liu Zhi, Hu Qiong, et al. Test bench control system of construction machinery hybrid power system[J]. Journal of Vibration, Measurent & Diagnosis, 2013，33(1)：144-148.(in Chinese)

[12]袁子荣，吴张永，袁锐波，等.新型液压元件及系统集成技术[M].北京：机械工业出版社，2011:110-113.

[13]何存兴.液压元件[M].北京：机械工业出版社，1982:395-398.

[14]任明章.机械振动的分析与控制以及计算方法[M] .北京：机械工业出版社，2011:57-63.

[15]宋鸿尧，丁忠尧.液压阀设计与计算[M]. 北京：机械工业出版社，1980:60-65.

10.16450/j.cnki.issn.1004-6801.2016.01.003

��研究发展计划(“九七三”计划)资助项目(2013CB035404)

2013-12-27；修回日期：2014-03-07

TH137.5; TP391.9

杨忠炯，男，1964年7月生，教授。主要研究方向为车辆传动及液压元件性能分析。曾发表《Dynamic characteristics of hydraulic power steering system with accumulator in load-haul-dump vehicle》(《Journal of Central South University of Technology》2004，Vol.11，No.4)等论文。 E-mail：yzj7072@126．com 通信作者简介：周振峰，男，1989年11月生，硕士。主要研究方向为液压元件性能分析。 E-mail：corpse1114@163.com