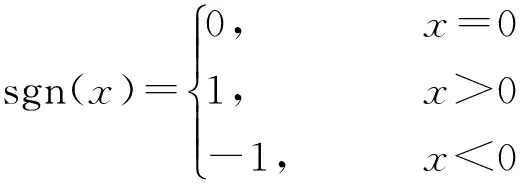基于人工鱼群算法的位移型阻尼器位置和参数的优化方法
闫维明, 杲晓龙, 谢志强, 彭凌云
(北京工业大学 建筑工程学院,北京 100124)
基于人工鱼群算法的位移型阻尼器位置和参数的优化方法
闫维明, 杲晓龙, 谢志强, 彭凌云
(北京工业大学 建筑工程学院,北京100124)
摘要:对耗能减震结构中,阻尼器参数和位置决定着结构的减震效果。基于人工鱼群算法提出一种针对位移型阻尼器优化设计的人工鱼群优化模型,模型面向以有限元模型表示的多维多自由度实际结构,对各层位移型阻尼器的位置和参数进行优化。针对结构中添加位移型阻尼器会使结构层剪力增大的问题,提出一种同时考虑结构各楼层层间位移角、各楼层加速度和层剪力变化的优化目标函数,同时利用均方根的形式更加有效的反应各响应在地震波峰值段的变化特性。结构减震控制优化设计时可根据结构的不同设计需求修正目标函数的加权系数。最后,通过数值算例验证本文优化模型的有效性。
关键词:耗能结构;位移型阻尼器;鱼群算法;阻尼器位置;阻尼器参数
结构减震控制是指在结构的特定部位添加耗能装置来减小结构的振动反应,以满足结构抗震安全性的要求。耗能减震结构中采用的阻尼器分为位移型阻尼器和速度型阻尼器。其中位移型阻尼器的性能主要由屈服力和初始刚度两个参数确定。采用位移型阻尼器对结构进行减震控制时阻尼器参数、位置、数量决定着阻尼器的减震效果,因此对阻尼器的参数、位置和个数进行优化计算有着重要意义,而优化算法、结构模型以及目标函数的选择对耗能减震体系的优化结果有着至关重要的影响。
国内外学者在阻尼器的参数和位置优化方面进行了深入研究,并提出不同的优化模型。Takewaki[1]基于结构传递函数,通过最小化结构层间位移角得到阻尼器的最优控制参数。Aydin等[2]通过建立与耗能器参数相关的拉格朗日方程,利用顺序搜索法求解耗能器参数的最优解。Mousavi等[3]通过建立与层间位移角相关的频域方程,利用逐步增量法得到阻尼器参数的最优解,并提出实际建筑结构的设计流程。Singh等[4-6]利用遗传算法求解阻尼器的最优参数。Singh等[7-10]利用遗传算法对阻尼器的位置进行优化。
以往的优化算法中[4-9],多数研究者将结构各层简化为两个平动或两个平动加一个转动的单质点体系,而实际结构是多维多自由度体系,模型的过度简化导致传统优化结果仅能给结构减震控制提供参考,无法直接应用于实际工程。同时已有关于位移型阻尼器的优化算法大多是对阻尼器参数和位置分别进行优化计算[9],但阻尼器的参数、位置和个数之间存在密切关系,以往的串行优化模式极有可能丢失系统的最优解。近年来,智能算法快速发展并成为解决多目标优化问题的有效手段。在这些智能算法中,人工鱼群算法具有并行性、简单性、快速性等特点,因此在多目标优化方面得到了广泛关注和应用。周丽萍等[11]利用鱼群算法对钢结构-控制系统进行协同优化设计。李亮等[12]利用鱼群算法求解两个复杂土坡的最小安全系数。已有成果表明利用鱼群算法求解结构减震控制中的多目标优化问题具有可行性和优越性。此外,当采用位移型阻尼器对结构进行减震控制时,会出现结构构件内力增加的情况[13],构件内力的增加是由于结构层剪力的增大而引起的,而已有的阻尼器优化目标函数较少考虑层剪力的变化,很可能影响实际的减震效果。
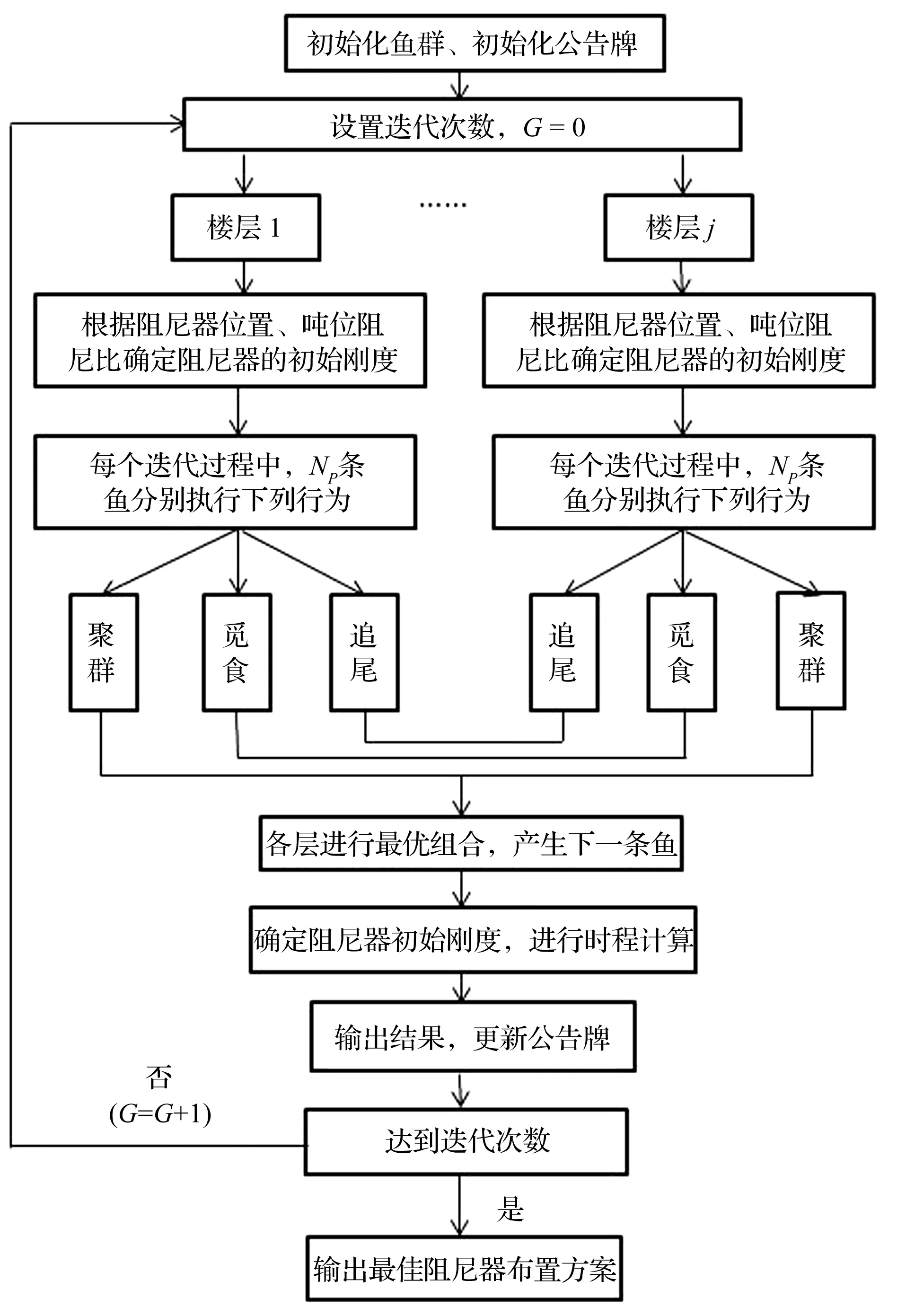
针对上述研究中存在的问题,本文建立了一种面向实际减震结构的位移型阻尼器优化模型。提出考虑层剪力变化的优化目标函数,目标函数中引入均方根的概念,更加有效的反应结构各响应在地震波峰值段的变化特性。通过构建优化算法与有限元软件的接口,使优化算法能够直接指导结构有限元模型的建立和调整。在优化过程中,通过限定阻尼器在多遇地震时提供给结构的附加阻尼比对位移型阻尼的参数和位置进行同步优化。此外,通过伪并行计算思想的引入,即在每次迭代计算时首先进行各层寻优,然后再整合各层优化结果进行整体分析最终得到最优解。
1阻尼器参数和位置优化的数学模型
1.1优化目标函数的建立
结构各层加速度、层间位移角和层剪力都是影响结构安全性和舒适度的重要指标,阻尼器的参数和位置优化的目的就是在阻尼器个数一定的条件下,求解阻尼器的最优参数和最优布置位置,使得上述控制指标对应的数值尽量小。介于目标函数中单一的控制指标可能会造成其他控制指标的增大[9],同时为了更加有效的反应各指标在地震波峰值段的响应大小,本文目标函数采用有控结构在地震作用下,时程分析得到的各层加速度、层间位移角和层剪力在地震波峰值段的均方根数值的最大值与其相应的无控结构对应的各响应的均方根的最大值比值的无量纲线性组合。通过改变加权系数的大小决定对各个指标的优化控制程度,定义目标函数如下:
Z=sum(σdi)
(1)
式中:
(2)
式中,wA、wB、wC分别代表各项的加权系数,σAi,max、σBi,max、σCi,max分别代表有控结构第i层的层间位移角、绝对加速度和层剪力在峰值段均方根的最大值。σA0i,max、σB0i,max、σC0i,max分别代表无控结构第i层的层间位移角、绝对加速度和层剪力在峰值段均方根的最大值。均方根的表达式为:
(3)
式中,n为地震波峰值段的步数,xi为地震波作用下各响应。
1.2优化参数关系的确定
为了使位移型阻尼器在设防和罕遇地震下更加有效地保护主体结构,阻尼器在设防地震作用下提供给结构的附加有效阻尼比应大于多遇地震作用下的附加有效阻尼比[14]。本文优化模型中通过限制多遇地震作用下位移型阻尼器提供给结构的附加阻尼比来满足上述要求。同时为了减少优化变量,推导了附加有效阻尼比、阻尼器的参数和位置之间的关系,推导过程如下:
位移型阻尼器一般通过与连接件的串联布置在结构的层间位置,假定位移型阻尼器的本构关系为图1所示的理想弹塑性模型,包括2个参数:弹性刚度Kd、屈服强度fy。
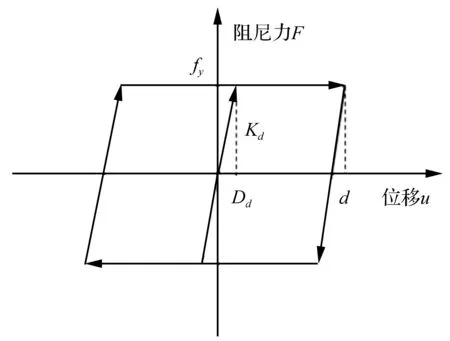
图1 位移型阻尼器滞回模型Fig.1 Hysteretic model of the displacement-based energy dissipative devices
《建筑抗震设计规范》(GB 50011-2010)[15]规定,消能部件附加有效阻尼比可按下式估算:
(4)
式中,ζa为消能减震结构的附加有效阻尼比;Wcj为第j个消能部件在结构预期层间位移下往复一周所消耗的能量;Ws为设置消能部件的结构在预期位移下的总应变能。
不计及扭转影响时,消能减震结构在水平地震作用下的总应变能,可按下式估算:
Ws=(1/2)∑Fiui
(5)
式中:Fi为质点i的水平地震作用标准值;ui为质点i对应于水平地震作用标准值的位移。
图1所示的单个位移型阻尼器滞回耗能计算公式如下:
Wcj=4KdDd(d-Dd)=4fy(d-Dd)
(6)
式中,Kd为阻尼器的初始刚度;Dd阻尼器的屈服位移;d为阻尼器两端的位移。fy为阻尼器的屈服力。
假定整个结构总共添加nf个阻尼器,所有阻尼器的耗能相等。由式(3)可得单个阻尼器的耗能可表示为:
Wcj=4πWsξa/nf
(7)
根据式(5)~式(6)可求得各阻尼器的初始刚度与阻尼器屈服力、消能减震结构总应变能、阻尼器的两端位移、消能部件附加给结构的有效阻尼比之间的关系如下:
(8)
模型在优化计算时,阻尼器的位置确定后可确定阻尼器两端的位移d,优化计算时可根据阻尼器的个数nf和屈服力fy和结构的应变能Ws确定阻尼的初始刚度。
1.3约束条件
(1)
0 (9) 0 (10) 式中,f、k分别指由阻尼器性能决定的阻尼器的吨位和初始刚度。 (2) θimax-θ≥0 (11) 式中,θimax和θ分别指结构的各层层间位移角最大值和规范规定的层间位移角限制。 (3) ξa-ξ0=0 (12) 式中,ξa指阻尼器附加给结构的有效阻尼比,ξ0指为保证位移型阻尼器在设防和罕遇地震下更加有效地保护主体结构而设定的阻尼器在多遇地震作用下提供给结构的附加阻尼比。 (4) 阻尼器的布置位置需要满足建筑要求,阻尼的个数可根据工程预算初步确定。 2阻尼器参数和位置的优化 2.1人工鱼群算法的优化原理 人工鱼群算法[16]是集群智能思想的一个具体应用,它不需要了解问题的特殊信息,只需要对问题进行优劣比较,算法主要通过单条人工鱼的觅食、聚群和追尾三个个体行为来寻求全局最优值。算法具有并行性、简单性、全局性、快速性、跟踪性等特点。算法中随机因素少,基本上可以步步向最优搜索。本文在基本人工鱼群算法的基础上开发伪并行鱼群算法优化模型,将其用于位移型阻尼器的参数和位置的优化。 人工鱼状态{X}=(x1,j,k,x2,j,k,…,xi,j,k,E),其中xi,j,k表示阻尼器的空间位置,i表示第i条人工鱼,j表示第j个楼层,k表示第k个阻尼器,{E}为阻尼器的参数向量。di,j=‖Xi-Xj‖表示人工鱼个体之间的欧式距离。本文距离可以表示为:假定两个决策变量A={a1,a2,…,an}和B={b1,b2,…,bn},A和B分别代表两条鱼中的某一楼层阻尼器的位置。则它们之间的距离可表示为: (13) (14) 人工鱼的觅食行为是鱼类的本能行为之一,表现为鱼在视野范围内的探寻活动,该行为保证人工鱼向最优状态持续行进。本文人工鱼在觅食行为中通过寻求各层层间位移角最大值对应的竖向构件,在距离最大层间位移角对应的竖向构件最近的位置添加阻尼器来指导人工鱼的游动方向,并通过给定次数的迭代计算使得人工鱼向着最优方向行进。人工鱼追尾行为,是一种向邻近的有着最高适应度的人工鱼追逐的行为,在算法中可以理解为是向附近的最优伙伴靠近的过程。假定人工鱼当前状态Xi,探索当前领域内(di,j 2.2人工鱼群算法的优化过程 基于上述基本人工鱼群算法的原理、优化参数及优化目标,在多遇地震作用下对添加位移型阻尼器的结构进行优化时,为了使位移型阻尼器在设防和罕遇地震下更加有效地保护主体结构,要求阻尼器在多遇地震作用下提供给结构的附加阻尼比不宜太大,建议取值1%。根据确定的附加阻尼比、阻尼器个数和吨位即可按照下述流程进行计算。 1) 首先初始化生成NP条人工鱼,初始化公告牌。根据建筑要求、结构特性和阻尼器个数在对应楼层,可添加阻尼器的位置随机布置阻尼器。 2) 假定各个阻尼器耗散相同的能量且每个楼层X、Y向布置相同参数的阻尼器。给定一个阻尼器的屈服力后可根据式(7)在给定附加有效阻尼比的情况下确定各层阻尼器的初始刚度,此时结构中的阻尼器单元被赋予属性,使得式(7)中的结构应变能发生变化,因此需要迭代计算调整阻尼器的初始刚度,直到多遇地震作用下阻尼器提供给结构的附加有效阻尼比满足约束条件(3)。 3) 启动迭代优化,各条人工鱼分别执行觅食、聚群和追尾行为,将其得到的优化结果与公告牌进行对比并及时更新公告牌。 4) 对不同吨位阻尼器下对应的优化结果进行对比分析,在优化结果中选择合理的阻尼器参数和布置方式。 5) 用规范规定的其他地震波对优化结果进行回归验证,判断得到的阻尼器优化布置方案在其它地震波作用下时能否使结构满足规范要求。 综上所述,位移型阻尼器参数和位置的优化过程如图2所示。 图2 算法流程图Fig.2 Flow chart of algorithm 图3 结构三维模型Fig.3 Structure model of three-dimensional 图4 各条地震波对应反应谱与规范反应谱的比较Fig.4 The comparison between the response spectra of every seismic waves and standard response spectra 3算例 本文优化算法在MATLAB平台上开发,建立了MATLAB与SAP2000有限元软件的接口,结构计算在SAP2000中完成。 某钢筋混凝土框架结构地下1层,地上6层,平面尺寸为57 m×16.3 m,结构总高度28.5 m。结构三维透视图见图3。按《建筑抗震设计规范》(GB50011-2010)要求抗震设防烈度为8度,设计基本地震加速度为0.30 g,设计地震分组为第二组,建筑场地类别二类,设计地震反应谱特征周期0.4 s。该结构主要问题是多遇地震作用下结构的层间位移角最大值X向为1/458,Y向为1/337,超过规范限值要求,拟通过在结构中布置位移型阻尼器使得结构满足规范要求。根据结构特性、场地类别选取2条天然场地波和1条人工波对结构进行分析,地震波峰值加速度为110 gal。本文优化时选用对无控结构响应最大的人工波激励结构,同时验算罕遇地震作用下结构各响应的变化情况。各地震波影响系数曲线与规范反应谱的对比如图4所示。 鱼群算法中各参数选择:人工鱼的总个数为8,视野范围为7,拥挤度因子为8,尝试次数为10,总迭代次数为15,移动步长为4。每条人工鱼代表一种阻尼器布置方案,本次优化时分别在结构的1~5层每层各布置8个位移型阻尼器。分别取屈服力40~100 t的阻尼器按照第2节所述优化过程对各位移型阻尼器进行位置和初始刚度的优化。 为了说明本文目标函数对结构层剪力控制的有效性,选用表1所示的两种不同加权系数对应的目标函数对结构进行优化。目标1和目标2分别指目标函数中考虑和不考虑层剪力的变化。图5~图6给出了选择不同吨位阻尼器时两种目标函数下模型的迭代优化过程。 表1 加权系数 图5 目标1对应迭代过程中目标函数的变化Fig.5 Transformation progress of function for the first goal 图6 目标2对应迭代过程中目标函数的变化Fig.6 Transformation progress of function for second goal 从图5和图6可以看出目标函数中不考虑层剪力的变化时,阻尼器吨位的越大,对目标函数的优化结果越好,阻尼器吨位取100 t时得到的优化结果最佳。目标函数中考虑层剪力变化后, 80 t的阻尼器对应的优化结果最好。表2给出了两种阻尼器布置方案对应的各层位移型阻尼器的初始刚度,可以看出,由于本文模型中限定了阻尼器提供给结构的附加有效阻尼比,因此吨位大的阻尼器对应的阻尼器的初始刚度偏大,间接表明本文目标函数对位移型阻尼器初始刚度的一个约束效果。 表2 阻尼器参数优化结果 按照上述得到的阻尼器的优化布置方案在结构中布置阻尼器,为了表明文中优化模型对阻尼器位置优化的有效性,在结构1~5层的四个边角处每层布置8个阻尼器,阻尼器的参数选取表2中目标1对应的阻尼器参数。利用时程分析方法,计算各有控结构及无控结构各层层间位移角、加速度和层剪力在上述3条地震波作用下的峰值,根据计算结果绘制结构各响应峰值对比图。限于篇幅,本文仅给出三条波作用下多遇地震和罕遇地震对应的结构层间位移角和层剪力的包络曲线,如图7~图10所示。表3~表4给出多遇地震和罕遇地震作用下各有控结构各响应最大峰值和最大均方根值的减震效果对楼层的平均值。 图7 多遇地震作用下层间位移角最大值优化对比Fig.7 The comparison of maximum story drift under frequent earthquake 图7~图8及表3可以看出:多遇地震作用下两种控制方式均能使结构的层间位移角满足规范要求,采用目标2对应的优化方案时,多数楼层的层间位移角峰值要小于目标1对应的层间位移角峰值,但目标2对应的层剪力峰值均大于目标1,甚至部分楼层层剪力大于原结构。在各楼层边角处均匀布置阻尼器时,层间位移角响应较目标1和目标2对应的结果偏大,层剪力较目标1整体上略微偏大。图9~图10及表4可以看出:罕遇地震作用下,结构的层间位移角均能满足规范要求,由于罕遇地震作用下结构中部分构件已进入非线性阶段,减震效果相对多遇地震有所减小。目标2对应的结构层间位移角峰值最小,目标1对应的层间位移角峰值介于目标2和无优化之间,目标1对应的结构层剪力均小原结构,而目标2和无优化对应的部分楼层层剪力会出现增大的情况,表明本文提出的目标函数中考虑层剪力的必要性及本文优化模型的有效性。 表3 多遇地震作用下层间位移角和层剪力减震效果平均值比较 注:表中数据意义为“目标2(目标1)[无优化]”。 表4 罕遇地震作用下层间位移角和层剪力减震效果平均值比较 注:表中数据意义为“目标2(目标1)[无优化]”。 图8 多遇地震作用下层剪力最大值优化对比Fig.8 The comparison of maximum story shear force under frequent earthquake 图9 罕遇地震作用下层间位移角最大值优化对比Fig.9 The comparison of maximum story drift under rare earthquake 图10 罕遇地震作用下层剪力最大值优化对比Fig.10 The comparison of maximum story shear force under rare earthquake 4结论 本文在人工鱼群算法的基础上提出一种针对位移型阻尼器位置和参数优化的优化数学模型,并建立了优化算法与有限元软件的接口, 实现了面向三维建筑结构的位移型阻尼器优化设计。可以直接在实际工程中应用,设计人员仅需根据结构的特征修正目标函数的加权系数及觅食行为中的指导因子即可得到阻尼器的优化布置方案。算例表明了该种优化模型的有效性。 在结构中添加位移型阻尼器后,有时会引起结构层剪力的增加,本文提出一种考虑层剪力的优化目标函数,采用均方根描述结构的响应,能够更加有效的考虑结构各响应在地震波峰值段的特性。算例验证了本文优化目标函数的有效性。 实际减震设计时,可根据工程预算确定阻尼器个数,根据结构需求确定阻尼器添加的楼层,运行优化模型,对比不同吨位的优化结果,选择充分满足结构适用性和安全性的阻尼器布置方案。 致谢:感谢教育部学术创新团队“土木抗震减震”和北京市属高等学校创新团队建设与教师职业发展计划项目资助。 参 考 文 献 [1] Takewaki Ι. Optimal damper placement for minimum transfer functions Earthquake [J]. Engineering and Structural Dynamics,1997, 26(11):1113-1124. [2] Aydin E, Boduroglu M H, Guney D. Optimal damper distribution for seismic rehabilitation of planar building structures[J]. Engineering Structures,2007,29(2):176-185. [3] Mousavi S A, Ghorbani-Tanha A K. Closure to “Discussion on ‘Optimum placement and characteristics of velocity-dependent dampers under seismic excitation’ by SA Mousavi and AK Ghorbani-Tanha” by Izuru Takewaki[J]. Earthquake Engineering and Engineering Vibration,2013, 12(4): 681-682. [4] Singh M P, Moreschi L M. Optimal seismic response control with dampers[J]. Earthquake Engineering & Structural Dy-namics, 2001, 30(4): 553-572. [5] Moreschi L M, Singh M P. Design of yielding metallic and friction dampers for optimal seismic performance [J]. Earthquake Engineering & Structural Dynamics, 2003,32(8): 1291-1311. [6] 李钢, 李宏男. 位移型耗能减震结构优化设计[J]. 振动与冲击,2007,26(4):65-68. LI Gang, LI Hong-nan. Optimum design of displacement-based energy dissipative devices [J]. Jouranl of Vibration and Shock,2007,26(4):65-68. [7] Singh M P, Moreschi L M. Optimal placement of dampers for passive response control [J]. Earthquake Engineering & Structural Dynamics, 2002, 31(4): 955-976. [8] 黄铭枫,唐家祥. 高层建筑粘弹性阻尼器的优化设置[J]. 华中科技大学学报,2001,29(11):73-75. HUANG Ming-feng, TANG Jia-xiang. Optimum installation of the viscoelastic dampers[J]. Journal of Huazhong University of Science and Technology,2001,29(11):73-75. [9] 曲激婷,李宏男,李钢. 位移型消能器在结构减震控制中的位置优化研究[J]. 工程力学,2009,26(1):43-48. QU Ji-ting, LI Hong-nan, LI Gang. Optimal placement of displacement-based energy dissipative devices for passive response control[J]. Engineering Mechanics, 2009,26(1):43-48. [10] 乌兰,李爱群,沈顺高. 基于遗传算法的偏心结构粘滞阻尼器优化布置研究[J]. 工程抗震与加固改造,2014,36(2):1-7. WU Lan, LI Ai-qun, SHEN Shun-gao. Optimal distribution of viscous damper for eccentric structure by genetic algorithm[J]. Earthquake Resistant Engineering and Retrofitting, 2014,36(2):1-7. [11] 周丽萍,凌云,徐斌. 基于鱼群算法的耦合地震作用下钢结构-控制系统协同优化设计[J]. 工业建筑,2014,44(7):164-169. ZHOU Li-ping, LING Yun, XU Bin. Integrated optimization of steel structure and control system under coupling earthquake based on artificial fish awarm algorithm[J]. Industrial Construction,2014,44(7):164-169. [12] 李亮,迟世春,林皋. 禁忌鱼群算法及其在边坡稳定分析中的应用[J]. 工程力学,2006,23(3):6-10. LI Liang, CHI Shi-chun, LIN Gao. Tabu fish swarm algorithm and its application to slope stability analysis[J]. Engineering Mechanics, 2006,23(3):6-10. [13] 李钢, 李宏男. 位移型耗能减震结构对框架柱轴力影响的研究[J]. 建筑结构,2009,39(2):25-27. LI Gang, LI Hong-nan. Study on influence of column axial force on the dissipative buildings[J]. Building Structure, 2009,39(2):25-27. [14] 闫维明,王维凝,彭凌云. 不同水准地震作用下铅阻尼器附加给结构的有效阻尼比及其设计取值研究[J]. 工程力学,2014,31(3):173-180. YAN Wei-ming, WANG Wei-ning, PENG Ling-yun. Study on the additional damping ratio provided by lead dampers and its design values under different earthquake standards[J]. Engineering Mechanics, 2014, 31(3):173-180. [15] GB 50011-2010, 建筑结构抗震规范[S]. 北京: 中国建筑工业出版社, 2010. [16] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践, 2002, 22(11): 32-38. LI Xiao-lei, SHAO Zhi-jiang, QIAN Ji-xin. An optimizing method based on autonomous animats: fish-swarm algorithm[J]. Systems Engineering-Theory & Practice,2002,22(11): 32-38. Optimization method for the placements and parameters of displacement-based dampers using artificial fish swarm algorithm YAN Wei-ming, GAO Xiao-long, XIE Zhi-qiang, PENG Ling-yun (The College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China) Abstract:In an energy dissipation structure, the seismic mitigation effect of dampers is depended on their parameters and placements. An optimized model based on artificial fish swarm algorithm, was proposed for the optimal design of displacement-based dampers. The model can be applied in structural finite element models with multi dimensions and degrees of freedom to determinate the placements and parameters of displacement-based dampers in each story. In order to deal with the increment of story shear force after installing displacement-based dampers, an optimized objective function was proposed, in which the variation of maximum story-drift angle, story acceleration and story shear force was considered, and the form of root mean square (rms) was adopted to reflect the vibration properties of each story’s responses in the process of earthquake wave excitation more effectively. In the optimal design process of the energy dissipation structure, the weighting coefficients of the objective function can be flexibly adjusted according to the design demands. Some examples were illustrated to verify the effectiveness of the new mathematic model. Key words:dissipative structure; displacement-based dampers; fish swarm algorithm; placement of damper; parameter of damper 基金项目:国家自然科学基金项目(51378039;51421005);北京市教委科技计划面上项目(KM201110005021) 收稿日期:2015-01-25修改稿收到日期:2015-04-25 通信作者杲晓龙 男,硕士,1990年7月生 中图分类号:TU352.1 文献标志码:A DOI:10.13465/j.cnki.jvs.2016.10.011 第一作者 闫维明 男,博士,教授,1960年7月生