岩石类脆性材料动态压剪耦合特性研究

徐松林， 周李姜， 黄俊宇， 章　超， 胡时胜

(中国科学技术大学 中国科学院材料力学行为和设计重点实验室，合肥　230027)

岩石类脆性材料动态压剪耦合特性研究

徐松林， 周李姜， 黄俊宇， 章超， 胡时胜

(中国科学技术大学 中国科学院材料力学行为和设计重点实验室，合肥230027)

摘要：岩石具有复杂的细微观结构，其宏观力学性能表现出明显的加载路径敏感性和应变率效应。应用基于改进的SHPB装置，对花岗岩、大理岩和砂岩等三类岩石进行了五种倾角的准静态和动态压剪联合加载实验，较系统地讨论了与岩石应力应变关系曲线的拟线性阶段的斜率、破坏强度等有关的加载路径敏感性和应变率效应。结果表明：岩石的法向模量、切向模量和破坏强度都有明显的压剪耦合效应(即加载路径敏感性)和应变率效应；比较而言，法向模量对剪切应力的依赖性强于剪切模量对法向应力的依赖性。基于Drucker-Prager(D-P)准则和考虑压剪耦合效应的修正的D-P准则拟合岩石的动静态破坏面，拟合结果表明：岩石的内黏聚力有一定的应变率效应，内摩擦角的应变率效应不明显；修正的D-P准则可以描述压剪耦合效应。并探讨了大理岩的后继屈服面和岩石应力应变关系的描述问题。此研究提供了一种确定岩石动态强度参数的方法，表明进行压剪联合加载实验研究有助于揭示复杂应力状态下岩石的动静态力学性能。

关键词：冲击动力学；分离式Hopkinson压杆(SHPB)；压剪复合加载；加载路径；岩石材料

岩石由固体矿物颗粒组成的骨架和孔隙、孔隙填充物构成，具有典型的跨尺度、非均质、多组元且多相的复杂结构。因此，即便是在单轴应力作用下，在岩石内矿物颗粒边界和孔隙周围，其应力状态也非常复杂。岩石的宏观力学响应是这些局部的复杂应力综合作用的结果。受地质作用和工程行为的影响，工程中的岩石具有更复杂的结构，处于更复杂的应力状态，宏观力学响应表现出非均匀和各向异性等特点。与金属材料不同，岩石在拟线性加载阶段就表现出非均匀和各向异性，受加载路径的影响较大，反映出较强的压剪耦合效应[1-2]。这种耦合效应在一定程度上将劣化岩石的强度[1-3]，因此，研究动静态载荷作用下岩体压剪耦合效应对于认识工程岩体和进行合理工程设计有着十分重要的意义。

加载路径效应反映的是岩石沿不同的加载过程达到同样的状态，如应力或应变状态或屈服状态，试样表现出不同的应变或应力或屈服特性，这是岩石内部由于微缺陷的存在而在不同加载过程产生程度不同的不可逆变形量的累积而导致的[1]。加载路径效应是岩土介质非常重要的属性。准静态下岩石加载路径效应的研究较多，主要集中在：等围压三轴压缩实验[4]、真三轴压缩实验[5-6]，以及直接剪切实验[7]等等。其中真三轴压缩实验采用立方体试件，分别用油压和承压板提供设计的σ2(第二主应力)和σ3(第三主应力)，通过改变这两个主应力值，得到不同加载路径下岩石的强度。准静态下的实验和理论探讨较多，这里不赘述。本文主要关注动荷载作用下的压剪耦合效应，对比准静态而言，更复杂，但更能反映岩石材料的性质。动荷载下，岩石不同加载路径的实验研究主要有：① 动态等围压三轴试验[8-9]，采用圆柱试件，用油压腔体给岩石试件施加设计的围压以提供压剪加载路径，通过改变围压，可得到多种加载路径下的岩石剪切强度，属于主动围压试验；② 被动围压试验[10-11]，采用圆环对圆柱岩石试件进行限定，但是加载过程试件周围限定环的压力随环的变形而发生变化，其状态为一维应变和一维应力的一个中间状态；③ 三轴SHPB试验(Tri SHPB)[12-13]，试件的侧向通过侧向杆施加恒定的压力；等等。以上研究的主要是加载过程的不同加载路径。同时，对于岩石类脆性材料而言，卸载过程也会产生材料局部的断裂[4,14]，也会产生不可逆变形量的累积。这些研究结果表明了岩石材料压剪耦合等加载路径效应的复杂性，进行研究具有相当的难度。同时，动态载荷作用下岩石的应变率效应更加重了这种复杂程度。进行相应的实验研究，对实验技术、设备，以及岩石试件加工等方面都具有较高要求，尤其是动态实验技术，其原理相对更复杂，因此，目前得到的实验数据不是很好分析，实验数据处理方面存在一些不确定之处[15-16]。

为进行岩石压剪联合动特性的研究，本实验室发展了一种较简单的通过添加具有不同倾角的垫块来实现压剪联合冲击的实验技术[15-17]：改变垫块斜面的倾角，此技术可实现压应力和剪应力按不同的比值进行加载。在研究山东花岗岩[3,15]和三峡花岗岩[16]的压剪动特性基础上，已经建立了较可靠的数据处理方法。基于此，本文将在此技术的基础上对花岗岩、大理岩和砂岩等三类岩石压剪联合冲击的实验结果进行较系统分析，讨论其压剪耦合特性和应变率效应，并初步探讨一种基于微力学机制的考虑压剪耦合特性和应变率效应的本构描述方法。

1岩石压剪联合冲击实验

1.1压剪联合冲击实验装置

图1所示为准静态(a)和动态(b)压剪联合加载实验示意图，对岩石试样的压剪联合加载主要通过添加具有不同倾角的斜垫块来实现。图中所示的试样构型由两个对称安装的相同的试样组成，即便加载装置提供的是单轴压缩载荷，但是，两个岩石试件均承受压应力和剪应力。准静态实验在MTS810实验系统上完成，如图1(a)所示。图中引伸计用来测试两垫块之间的变形量。准静态实验主要是为了更好地理解岩石压剪耦合行为，并为动态实验提供对比。动态实验在中国科学技术大学冲击动力学实验室的分离式霍普金森压杆上进行，如图1(b)所示。其基本思想是：由两个对称安装的岩石试样和部分斜垫块共同组成一个可满足SHPB实验的“试件”，即图1(b)中虚线框圈住部分。应用常规SHPB实验，测试此组合而成的复合“试件”的动态响应。由此，首先基于动态响应信号进行复合“试件”的载荷位移分析，然后对“试件”内进行受力分析，实现岩石试样正应力和剪切应力的分解，从而得到岩样的压剪动态响应特性。相关数据处理方法可参见文献[15-16]，这里不赘述。

图1(b)中使用的杆材为钢材，子弹直径为37 mm，长度为300 mm；入射杆为变截面锥杆，直径由37 mm渐变为74 mm，总长度为3 200 mm，其中锥形段长度为370 mm；透射杆直径为74 mm，长度为1 800 mm。采用变截面杆是为了使用更大尺寸的试样。在动态实验的同时，可使用Phantom V12.1高速相机全程跟踪拍摄，以进行动态加载过程的变形场的测试分析，并监测加载过程岩石试件与垫块之间的接触界面是否发生滑动，以评价实验的有效性。

1.2试样及实验条件

选用三类共四种岩石的实验作比较，进行分析。其中火成岩类有两种：均匀性比较好的细颗粒山东花岗岩和中等颗粒、并有一定风化痕迹的微风化三峡花岗岩，主要成分为石英、长石和云母，孔隙率小于1%；层积岩类为彭山砂岩，颗粒直径在1/16～2 mm，孔隙率在12%～18%；变质岩类为大理大理岩， 孔隙率约1%～3%。采用方形试样。考虑到SHPB实验中应力均匀性和岩样均匀性要求，采用“三波法”对波校核[18]，试件的长径比选择为0.5～1.0。随垫块倾斜角度增加，长径比适当减小。岩样尺寸约为25 mm×25 mm×20 mm。试件表面进行精细加工，同时，同一个实验中组装的两个岩样高度差控制在0.01 mm以下。

图1　岩石压剪联合加载实验

对山东花岗岩进行了三种不同的应变率，即准静态下的3×10-5s-1和动态冲击下的50 s-1、100 s-1的实验；对三峡花岗岩、大理大理岩进行了准静态(应变率3×10-5s-1)和动态冲击(应变率100 s-1)实验，实际实验中部分三峡花岗岩试件的应变率约为65 s-1；对彭山砂岩进行了动态冲击(应变率100 s-1)实验。其中，彭山砂岩因为准静态的数据较多，且受试样数量的限制，只集中进行了动态实验。准静态实验是为了给动态实验提供参考和分析依据。动静态下压剪联合加载

1.3法向和切向应力应变关系

准静态压剪联合加载实验结果如图2～图4所示，图中依次列出了三峡花岗岩、大理大理岩和彭山砂岩的实验曲线。山东花岗岩的数据可参见文献[3,15]，未列出，但参与后面的对比分析。其中图2(a)、图3(a)和图4(a)为载荷-位移曲线，由SHPB实验中入射杆和透射杆上的数据计算得到。然后，利用文献[16]公式(2)，对三峡花岗岩、大理大理岩和彭山砂岩分别取泊松比为0.18、0.20和0.21，即可将图2(a)、图3(a)和图4(a)的载荷-位移曲线分解为三类岩石试样上的法向应力应变关系(图2(b)、图3(b)和图4(b))和切向应力应变关系(图2(c)、图3(c)和图4(c))。由此可见，岩石应力应变关系具有四个阶段，即初期的非线性压缩/剪切密实阶段、拟线性压缩/剪切阶段、非线性压缩/剪切阶段，以及破坏阶段。岩石压剪联合加载过程最明显的特征为：① 随着倾角的增加，无论是准静态加载过程还是动态加载过程，应力应变关系越来越偏离单轴压缩曲线，曲线的斜率越来越小；以三峡花岗岩为例(图2)，倾角在0°～45°范围内，拟线性阶段压缩/剪切应力应变关系曲线斜率有一定变化，但变化不大；但是当倾角较大(超过45°)时，应力应变关系曲线斜率有较大的差异，尤其是倾角60°时，差异很大；当试样为较软、且含有较多孔洞和裂纹等细微观缺陷的大理岩(图3)和砂岩(图4)时，这种差异性就更大；② 随着倾角的增加，无论是准静态加载过程还是动态加载过程，其法向强度逐渐减小，对应的切向强度逐渐增加；③ 随着倾角增加，破坏应变逐渐增大；④ 同一倾角下，动态加载过程与准静态加载过程比较，无论是在应力应变关系曲线的斜率，还是极限强度方面都有较大的差异，动态的明显要高得多，具体可参见图3。因此，在岩石的强度和应力应变曲线的斜率两个方面均表现出明显的加载速率效应和加载路径相关性，这是岩石混凝土类材料与金属材料最大的差异，具体数据后面进行分析。上述图中均列出了倾角60°的数据，在高速摄影监控下，准静态加载时，实验过程试件与垫块之间未发现明显的滑动；但是动态加载过程，借助人工散斑场[3,15]可以监测到接触界面有一定的滑移。动态加载下，倾角60°的数据都反映出试件有多次压缩的过程，是一种“黏-滑”(stick-slip)运动交替发展的结果[2]。因此，动态加载下倾角60°度的数据仅有参考意义。比较而言，准静态下倾角60°的数据可靠一些，但是与其他倾角的对比结果表明：其行为有较大的差异，偏离了小倾角时的发展趋势。这涉及界面微滑移等机制，须深入探讨。

图2　三峡花岗岩动静态压剪联合加载实验曲线Fig.2 Experimental results of Sanxia granite under compression and shear loading

图3　大理大理岩动静态压剪联合加载实验曲线Fig.3 Experimental results of Dali marble under compression and shear loading

图4　彭山砂岩动态压剪联合加载实验曲线Fig.4 Experimental results of Pengshan sandstone under compression and shear loading

2岩石压剪耦合效应

2.1拟线性阶段的模量

拟线性阶段花岗岩准静态下弹性模量和剪切模量随倾角的变化如图5(a)所示。图中同时列出了三峡花岗岩和山东花岗岩的实验数据。图5(a)表明，对于山东花岗岩而言，当倾角小于45°度时，随着倾角的增加，法向模量具有一定幅度的降低，其趋势呈指数关系；而倾角高于45°时，法向模量迅速降低，其幅度远高于较低倾角时的情况；由于三峡花岗岩含有更多的细微观缺陷，其法向模量随倾角增加而降低的幅值明显要高得多。切向模量具有相同的趋势。其差异在于：切向模量对倾角变化的敏感性要低于法向模量。三峡花岗岩两类模量的倾角敏感性均比山东花岗岩强得多。这说明：两类花岗岩都具有较明显的加载路径敏感性；同时，这种敏感性与岩石试样的细微观结构有关，具有越丰富的孔洞、裂纹等细微观结构，岩石的路径敏感性越强。

Olsson等[19]监测岩石加载过程的声发射信息，发现初始加载阶段较多的声发射信号发生在试件的端部。由于岩石是有天然细微观缺陷的材料，在初始加载过程试件端部微缺陷要压缩闭合。McCall等[20]引进了P-M空间模型来描述岩石加卸载循环中的滞回环，认为：岩石试样由一定数量的张开裂纹和闭合裂纹组成，张开裂纹和闭合裂纹的数量随外载荷变化而发生调整，岩样宏观力学性能与这些张开裂纹和闭合裂纹的数量变化相联系。剪应力越大，张开裂纹越多；压应力越大，闭合裂纹越多。岩体宏观力学性能表现出对剪切载荷较强的敏感性；同样的原因，岩石对拉伸载荷更为敏感。由于细微观裂纹的存在，即便在简单的单轴加载条件下，岩样内裂纹局部均有剪应力或拉应力等存在，而不是单纯的压应力。因此，通常实验得到的单轴压缩强度也是复杂应力共同作用的结果。岩石加载路径效应就是这些细微观裂纹的张开和闭合数量随不同剪应力变化而调整的过程。岩样中初始缺陷越多，剪切应力影响越大，加载路径效应越明显。

不同加载速率下两类花岗岩法向和切向应力应变关系曲线的斜率随倾角的变化如图5(b)和图5(c)。一般而言，SHPB实验得到的应力应变关系的开始阶段不能直接用于模量的计算，为了与图5(a)中准静态性能进行对比分析，动态实验的法向/切向斜率取为对应应力应变关系曲线中应力超过60%极限强度时拟线性阶段的斜率。因数据点较多，为了说明变化趋势，图中趋势线采用指数函数拟合得到。由图可见：同一加载速率下，法向斜率随倾角增加基本呈指数衰减趋势；同一倾角下，法向斜率随加载速率增加呈递增趋势。岩石强度一般随应变率的增加呈对数递增关系，图5(b)中所示的法向斜率与应变率似也具有这种关系，但因为只有三种加载速率，下结论尚早。图5(c)中所示的切向斜率与此规律相同。由于倾角为60°度时，试件与垫块的接触界面可能发生滑移，数据点与其他倾角差别较大，因此，拟合趋势线的时候没有包含进去。对比图5(a)和图5(b)、(c)所示的结果表明：花岗岩的法向和切向模量均有较强的加载速率效应，且与加载路径有关。

由于岩土材料一般具有剪胀效应，剪应力作用会引起试样体积的变化，因此，具有较复杂的对应关系，即具有压剪耦合效应。Nelson等[21]引入变模量模型来描述土的体积模量和剪切模量。在变模量模型中，体积模量是静水压力的函数，剪切模量则是静水压力与等效剪应力的函数。这种假定有一定缺陷，尤其是在体积模量方面。基于以上实验数据，可认为：体积模量和剪切模量均为静水压力与等效剪应力的函数。由此，弹性模量也是静水压力与等效剪应力的函数。基于以上分析，考虑应变率效应和加载路径影响的弹性模量和剪切模量可表示为：

(1)

(2)

图5　两类花岗岩动静态应力应变曲线的斜率Fig.5 Slope of stress strain relationship of two granite under quasi-static and dynamic loading

大理岩和砂岩的动静态法向和切向斜率对比分别如图图6(a)和图6(b)所示。其趋势与以上讨论的花岗岩相似。由于这两类岩石具有更丰富的细微观缺陷，因此，其加载路径效应和应变率敏感性更强。

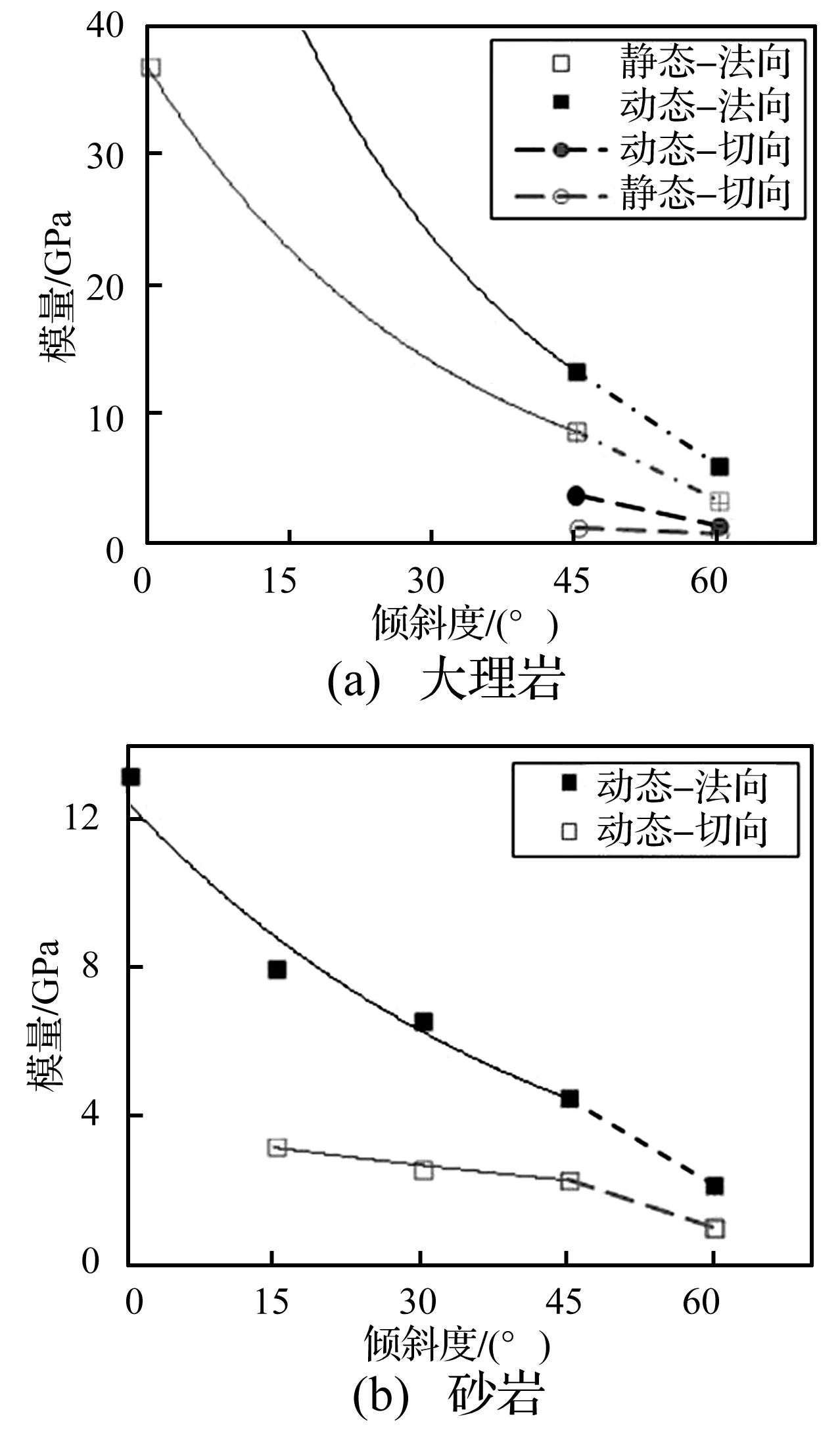
图6　大理岩和砂岩动静态应力应变曲线的斜率Fig.6 Slope of stress strain relationship of marble and sandstone under quasi-static and dynamic loading

2.2压剪耦合强度的分析

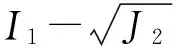
I1=σ

(3a)

(3b)

(4)

(5)

(6)

(7)

四类岩石的拟合结果分别见图7、图8和图9中虚线部分。由此可见：由于D-P准则考虑了岩石的拉压强度不对称性，可以同时考虑静水压(I1)和等效剪切载荷)的作用，在倾角小于45°范围，其拟合结果较好。但是，由于D-P准则没有考虑压剪耦合效应，因此，在倾角较大的区域，其拟合结果并不是很好。虽然这可能是压剪联合加载实验本身造成的，但是，对于较大倾角范围的屈服面描述需要进行相应的修正。因此，增加一个压剪耦合项对D-P准则进行修正，在平面和σ-τ平面内修正D-P准则表达式分别为：

(8)

(9)

对于纯剪切加载情况，可以得到：k1=τy，其中，τy为纯剪切时的剪切强度。

对于单轴压缩情况：

(10)

对于单轴拉伸情况：

(11)

由此，综合上述三种加载情况，可以得到：

(12a)

(12b)

对实验数据采用修正的D-P准则进行拟合。图7～图9中所示实线为采用修正的D-P准则拟合的结果。两类花岗岩拟合结果中β1的值比较小：山东花岗岩为0.07～0.09之间，三峡花岗岩为0.1～0.15之间。图7和图8中拟合结果表明，耦合项在倾角较大的区域可以取到一定的作用。图9中对大理岩和砂岩的拟合中β1的值比较大，达到了0.5～0.6，虽然拟合结果有所改善，但是，在倾角较大的区域仍存在一定差异。以上采用修正D-P准则进行实验数据的拟合，说明岩石的强度有较明显的压剪耦合效应，强度准则中须计入耦合效应的影响；同时，岩性不同，耦合效应存在较大差异。这些仍须基于微力学方法进行深入研究。

(a) σ-τ平面(a) σ-τ平面(a) σ-τ平面

(b) I1-J2平面(b) I1-J2平面(b) I1-J2平面图7 压剪联合加载下山东花岗岩动静态破坏面Fig.7FailuresurfaceofShandonggraniteunderquasi-staticanddynamiccompressionandshearloading图8 压剪联合加载下三峡花岗岩动静态破坏面Fig.8FailuresurfaceofSanxiagraniteunderquasi-staticanddynamiccompressionandshearloading图9 压剪联合加载下大理岩和砂岩动静态破坏面Fig.9Failuresurfaceofmarbleandsandstoneunderquasi-staticanddynamiccompressionandshearloading

2.3压剪联合加载过程的后继屈服面

分析图2～图4中法向和切向应力应变关系，虽然应力应变关系曲线可以分为4个阶段，但随倾角的不同，每个阶段所占的比重不一样。其中，拟线性压缩/剪切阶段随倾角的增加，线性段逐渐缩短，而且愈加不明显。因为拟线性阶段的结束对应岩石的屈服强度，因此，实验曲线也表明：随着剪切分量的增加，岩石更容易进入塑性状态。对比不同倾角下应力应变关系曲线，它们最大的区别是：进入非线性压缩/剪切阶段，即第三阶段或塑性阶段后，随着倾角的增加，岩石试件具有更大的应变，表现出一定塑性流动的特征。同时，此阶段的屈服应力随载荷和应变的增加有一定的增加，反应出岩石试件的塑性变形过程具有一定的塑性硬化特性。但是，岩石试件塑性硬化过程并不是平滑进行的，非线性压缩/剪切阶段曲线由多级台阶状曲线组成，表现出较明显的多次后继屈服，即多次塑性硬化的特征。这个现象在单轴压缩过程不是很明显，但在压剪联合加载过程表现得比较突出。以图3中大理大理岩的准静态实验为例，从初始进入塑性阶段开始，将不同倾角下法向和切向应力应变关系中这些台阶对应的应力状态依次列出，如图10所示。图中列出了从初始屈服到最后破坏，大理岩试件至少进行了4次明显屈服过程，也即进行了3次较明显的后继屈服。每一个后继屈服面都已经无法用单一的Mohr-Coulomb屈服准则、Hoek-Brown屈服准则，或Drucker-Prager准则来描述，需要这些准则与帽盖模型相结合[25]。这些后继屈服面展示了岩石从屈服向破坏发展的塑性发展历程。因此，压剪联合加载技术也给岩石的塑性硬化的研究提供较好的实验手段。当然，动态加载过程的后继屈服数据比较复杂，这里尚未涉及，须深入探讨。

图10　压剪联合加载下大理岩的后继屈服行为Fig.10 Subsequent yield surface of marble under compression and shear loading

3关于压剪耦合作用下应力应变关系的描述

以上对压剪联合加载过程的模量和破坏强度等进行了较系统讨论，这里将对压剪联合加载过程的本构关系的描述作一些探讨。基于Olsson等[19]监测的声发射信息和McCall等[20]的P-M空间模型，岩石试件可以看作是含有一定数量的张开和闭合的细微观缺陷的复合介质。岩石试件的宏观应力应变关系是这些细微观缺陷在外载荷作用下数量的调整和演化的综合结果：所谓调整是指在变形的初始阶段，微缺陷在张开或闭合状态之间发生转变；而演化则是非线性变形阶段，新的微缺陷成核，微缺陷的数目要增加。因此，细微观缺陷的发展和演化过程是描述岩石宏观应力应变关系的微力学机制。

微力学方法(Micromechanical Based Approach), 是一种基于微观机制的力学分析方法。其目的是从材料或结构的细微观机制出发来探讨宏观力学行为。实际上，国内外的相关论述比较多，但是尚没有统一的定义和公认的程序化的分析方法[26-27]。岩石中细微观缺陷的描述可采用三个几何参数：微缺陷的数密度(n)，即单位体积或面积中缺陷的个数；微缺陷的尺度，如长度(c)；微缺陷的角度，和状态参数：张开位移等。由此，可建立微缺陷数的动态演化方程。Bai等[26]得到了一个一维相空间中微损伤数密度分布函数的演化方程：

(13)

式中，t为时间，A为一个确定性函数。nN为一个表征随机过程的成核率密度函数。

对于岩石压缩过程也可以得到一个类似的方程：开始阶段不考虑微缺陷成核，nN=0；非线性阶段微裂纹生长，则nN快速发展。基于这种分析，假定微缺陷数与长度间满足Weibull分布，可初步得到描述岩石应力应变关系的表达式：

(14)

式中，σref，εref为参考应力和参考应变，m为材料参数。

式(14)可以很好地拟合倾斜角较小的应力应变关系，如倾斜角小于30°的数据。但是，大倾角的实验中应力应变关系表现出非常明显的非线性加载阶段，即有较明显的塑性硬化过程，采用式(14)拟合效果并不好。这时需要引进两个参考应变εrefy和εrefu，分别对应塑性屈服应变和破坏应变，由此，式(14)可推广为：

(15)

式中，m1和m2为材料参数。

虽然参数确定较麻烦，但式(15)可以较好地拟合压剪联合加载过程的本构关系。

4结论

本文应用改进的Hopkinson压杆(SHPB)装置，对山东花岗岩、三峡花岗岩、大理大理岩和彭山砂岩等4种岩石进行了在准静态和动态下五种加载路径的压剪复合加载实验，较系统地讨论了岩石的法向和切向模量，以及破坏强度的加载路径敏感性和加载速率效应。由此，基于D-P准则和修正的D-P准则进行了岩石强度曲面的拟合和岩石参数的加载速率效应讨论；并基于微力学观点，进行了压剪联系加载下应力应变关系描述方法的讨论。所得到的主要结论如下：

(1) 准静态下压剪联合加载实验表明：岩石的法向模量和切向模量随倾角的增大都有一定程度的减小，有较明显的压剪耦合效应。但是，切向模量对倾角变化的敏感性要低于法向模量。比较山东花岗岩、三峡花岗岩和大理大理岩的实验结果，可以发现：含有更多的细微观缺陷的岩石，其模量的倾角敏感性要强得多。这表明：压剪耦合效应源于与岩石试样的丰富的孔洞、裂纹等细微观结构。

(2) 对比三种应变率下的模量数据，岩石的法向模量和切向模量都具有明显的加载路径敏感性和应变率效应。而且，动态加载下的加载路径敏感性比准静态加载下强得多。

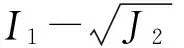
(4) 对大理大理岩应力应变关系曲线的非线性加载阶段进行分析，得到了大理岩从初次屈服到破坏过程中塑性屈服发展的过程，发现有3次较明显的后继屈服过程，即塑性硬化过程。

(5) 基于微力学体系的动态分析方法，提出了描述岩石压剪联合加载下应力应变关系曲线的方法。

参 考 文 献

[1] 席道瑛,徐松林.岩石物理与本构理论[M]. 合肥:中国科学技术大学出版社, 2016.

[2] 席道瑛,徐松林. 岩石物理学基础[M]. 合肥:中国科学技术大学出版社, 2012.

[3] 徐松林,章超,黄俊宇,等. 花岗岩压剪联合冲击特性与细观力学机制研究[J].岩石力学与工程学报,2015,34(10):1945-1958.

XU Song-lin, ZHANG Chao, HUANG Jun-yu, et al. Investigation of dynamic behavior and micromechanical mechanism of granite under combined compression and shear loading[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(10): 1945-1958.

[4] 徐松林,吴文,王广印,等.大理岩等围压三轴压缩全过程研究I：三轴压缩全过程及峰前峰后卸围压全过程试验[J].岩石力学与工程学报，2001,20(6):763-767.

XU Song-lin, WU Wen, WANG Guang-yin, et al. Study on complete procedures of a marble under triaxial compression I: testing study of complete procedures of triaxial compression and the processes of unloading at the pre-peak and post-peak[J]. Chinese Journal of Rock Mechanics and Engineering, 2001,20(6): 763-767.

[5] 许东俊, 章光，李廷芥，等.岩爆应力状态研究[J]. 岩石力学与工程学报,2000,19(2):169-172.

XU Dong-jun, ZHANG Guang, LI Ting-jie, et al. On the stress state in rock burst[J]. Chinese Journal of Rock Mechanics and Engineering,2000,19(2):169-172.

[6] 徐松林，吴文，白世伟，等.三轴压缩大理岩局部化变形的实验研究及其分岔行为[J].岩土工程学报，2001,23 (3): 296-301.

XU Song-lin, WU Wen, BAI Shi-wei, et al.Experimental studies of localization and bifurcation behaviors of a marble under triaxial compression[J].Chinese Journal of Geotechnical Engineering, 2001, 23(3): 296-301.

[7] 徐松林,吴文,张华，等.直剪条件下大理岩局部化变形研究[J].岩石力学与工程学报，2002, 21(6): 766-771.

XU Song-lin, WU Wen, ZHANG Hua, et al. Testing study on localization of a marble under direct shear[J]. Chinese Journal of Rock Mechanics and Engineering, 2002,21(6):766-771.

[8] Li H B, Zhao J, Li T J. Triaxial compression tests of a granite at different strain rates and confining pressures[J]. International Journal of Rock Mechanics and Mining Science, 1999,36:1057-1063.

[9] Li X B, Zhou Z L, Lok T S, et al. Innovative testing technique of rock subjected to coupled static and dynamic loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2008;45(5): 739-748.

[10] Chen W, Ravichandran G. An experimental technique for imposing dynamic multi-axial compression with mechanical confinement[J]. Experimental Mechanics, 1996,36: 155-158.

[11] Chen W, Ravichandran G. Dynamic compressive failure of a glass ceramic under lateral confinement[J] . Journal of Mechanics and Physical Solids,1997,45:1303-1328.

[12] Zhang Q B, Zhao J. A review of dynamic experimental techniques and mechanical behavior of rock material[J].Rock Mechanics and Rock Engineering,2013,47(4):1411-1478.

[13] Cadoni E. Mechanical characterization of rock materials at high strain-rate[C]//Rock Dynamics and Applications—States of Art. Hoboken: CRC Press, 2013: 137-148.

[14] Espinosa H D, Raiser G, Clifton R J, et al. Experimental observations and numerical modeling of inelasticity in dynamically loaded ceramics[J]. J Hard Materials, 1992,3(3/4): 285-313.

[15] 章超.数字图像方法在动态测试中的应用[D].合肥：中国科学技术大学，2014.

[16] 章超，徐松林，王道荣，等.花岗岩动静态压剪复合加载实验研究[J].固体力学学报，2014, 35(2): 115-122.

ZHANG Chao, XU Song-lin, WANG Dao-rong, et al.Experimental study of granite under combined compression-shear dynamic and quasi-static loading[J].Chinese Journal of Solid Mechanics, 2014, 35(2): 115-122.

[17] 郑文，徐松林，蔡超，等.基于Hopkinson压杆的动态压剪复合加载实验研究[J]. 力学学报，2012,44(1):124-131.

ZHENG Wen, XU Song-lin, CAI Chao, et al. Dynamic combined compression and shear loading technique based on SHPB testing[J].Acta Mechanica Sinica, 2012,44(1):124-131.

[18] Chen W, Song B. Split Hopkinson (Kolsky)bar: design, testing and applications[M]. New York: Springer, 2011.

[19] Olsson W A, Holcomb D J. Compaction localization in porous rock[J].Geophysical Research Letters,2000,27(21):3537-3540.

[20] McCall K R, Guyer R A. Equation of state and wave propagation in hysteretic nonlinear elastic materials[J]. Journal of Geophysical Research,1994,99(B12):23887-23897.

[21] Nelson I, Baron M L. Application of variable moduli models to soil behavior[J]. International Journal of Solids and Structures,1971,7(4):399-417.

[22] Drucker D C, Prager W. Soil mechanics and plastic analysis for limit design[J]. Quarterly of Applied Mathematics,10(2):157-165.

[23] 徐松林, 吴文, 张华,等. 大理岩单轴压缩过程的强度确定及其应变率影响[J]. 地下空间, 2001, 21(4): 272-275.

XU Song-lin, WU Wen, ZHANG Hua,et al. Analyses on strength of marble under uniaxial compression and influences of strain rate[J]. Underground Space, 2001, 21(4): 272-275.

[24] Zhao J. Applicability of Mohr-Coulomb and Hoek-Brown strength criteria to the dynamic strength of brittle rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(7):1115-1121.

[25] 徐松林，刘永贵，王道荣,等. 高孔隙率Al2O3微孔陶瓷压剪冲击动特性研究[J]. 高压物理学报,2013,27(5):662-670.

XU Song-lin, LIU Yong-gui, WANG Dao-rong, et al. Dynamic responses of alumina microvoid ceramics with high porosity under combined pressure and shear impact loading[J]. Chinese Journal of High Pressure Physics, 2013,27(5):662-670.

[26] Bai Y L, Ling Z, Luo L M, et al. Initial development of micro-damage under impact loading[J]. Journal of Applied Mechanics,1992,59: 622-627.

[27] 夏蒙棼，韩闻生，柯孚久，等. 统计细观损伤力学和损伤演化诱致突变(I) [J]. 力学进展，1995，25(1): 1-23.

XIA Meng-fen, HAN Wen-sheng, KE Fu-jiu, et al. Statistical meso-scopic damage mechanics and damage evolution induced catastrophe(I)[J]. Advances in Mechanics,1995,25(1): 1-23.

Dynamic coupled behavior of rock materials under combined compression and shear loading

XU Song-lin, ZHOU Li-jiang, HUANG Jun-yu, ZHANG Chao, HU Shi-sheng

(CAS Key Laboratory for Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, China)

Abstract:Since rocks are of complex structures at the micro and meso scales, they exhibit obvious load-path dependency and strain rate effect. Employing the modified split Hopkinson pressure bar (SHPB)device, a series of experiments were conducted to investigate the mechanical behaviors of three kinds of rocks, e.g. granite, marble, and sandstone, under quasi-static and dynamic combined compression and shear loading with five oblique angles. The load-path dependency and strain rate effect related to the slopes on stress strain relationship curves at the quasi-linear loading stage and the strength of rocks were analyzed in detail. The results show that normal, shear modulus and failure strength of rocks exhibit obvious strain rate effect and certain coupled compression-shear effect, which is also known as path-load dependency. The dependence of shear stress on normal modulus is stronger than that of normal stress on shear modulus. The Drucker-Prager(D-P) criterion and the modified D-P criterion, which consider the coupled compression and shear effect, were employed to fit the quasi-static and dynamic failure surfaces. The results show that the inner cohesion of rock exhibit certain strain rate effect, but the inner friction angle takes on little strain rate effect. Further discussions focus on the subsequent yield surfaces of marble and the description of stress strain relationship of rocks under combined compression and shear loading. These investigations provide a powerful method to determine strength parameters of rock materials under dynamic loading, and it is helpful to use the combined compression and shear experiments to investigate quasi-static and dynamic behaviors of rocks under complicated stress states.

Key words:impact dynamics; split Hopkinson pressure bar; combined compression-shear loading; load-path dependency; rock material

基金项目：国家自然科学基金(11272304;11472264)

收稿日期：2015-01-30修改稿收到日期：2015-06-05

中图分类号:TU452

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.002

第一作者 徐松林 男，博士，副教授，1971年1月生

E-mail:slxu99@ustc.edu.cn