从知识整合的角度尝试试题改编
2016-06-12 08:34安徽刘东莲
高中数理化 2016年10期
◇ 安徽 刘东莲
从知识整合的角度尝试试题改编
◇安徽刘东莲
对于某些知识整合度较高的试题,若利用以点及面的方式进行知识整合度的改编,往往可以将问题需要考查的知识,整合在类似的数学问题中,通过这些改编问题的求解,来锻炼学生的应变能力.
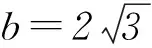
首先通过余弦定理得到角B的大小,那么所求的sinA+sinC中,尽管A、C都不确定,但A+C是定值,C可以随着角A的变化而变化,那么sinA+sinC可以表示成关于角A的函数关系式,利用角A的范围求解即可.

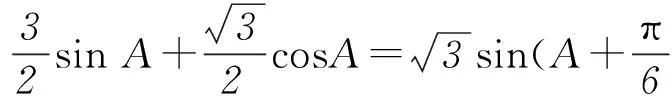




改编意图原题角A的取值范围没有约束,现将条件改为锐角三角形,即对函数定义域做出了约束,这种改编暗示学生对函数值域的求解应先研究定义域.


改编意图在解与三角形最值有关的问题中,常需要结合余弦定理与基本不等式,这种知识的整合性使用要引起师生的重视.


改编意图基本不等式的使用具备多重性,在解三角形问题中设计“求a2+c2的最大值”,将不等式知识整合使用推向了另一个高度,使学生对于整合知识使用有了多样性的认识.


改编意图解三角形中正弦定理、余弦定理与面积公式有着紧密联系,将试题进行关于面积方面的改编,自然水到渠成.


改编意图解三角形的问题还能和平面几何知识进行整合,比如中线、高线、重心、内心等,这样的一系列改编有助于整个知识体系的网络化、细致化,更能在这一知识的处理中做到以不变应万变.
总之,试题的研究是高考的生命力.教师不可仅要求学生做题,必须要有自身的创造力,这种创造力既研究了知识考查的热度、难度、分布,也提高了教师自身对于知识的进一步理解和掌控,对于高考试题研究和教学是必不可少的工作,更有助于教师自身的成长和发展.
(作者单位:安徽省枞阳县浮山中学)
猜你喜欢
法律方法(2022年2期)2022-10-20
福建基础教育研究(2022年4期)2022-05-16
语数外学习·高中版上旬(2022年2期)2022-04-09
法律方法(2021年3期)2021-03-16
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
河北理科教学研究(2020年1期)2020-07-24
数理化解题研究(2020年19期)2020-07-22
读写算(2019年5期)2019-09-01
中学课程辅导·教学研究(2017年29期)2018-02-26

