林分直径分布的Weibull参数估计系统研制
谢鹏芳,谢 敏,裴志涛,黄旭光,黄家荣,周俊朝
林分直径分布是指在林分内各种大小直径林 木按径阶的分配状态,也称为林分直径结构。无论在理论上还是在实际上,林分直径结构是最重要、最基本的林分结构,不仅因为林分直径便于测定,更是因为林分内各种大小直径的树木的分配状态,将直接影响树木的树高、干形、材积、材种及树冠等因子的变化[1]。在理论上它为许多森林经营技术及测树制表技术提供了依据。多数研究认为,林分直径分布拟合模型中3参数Weibull分布模型最优[2-5],对函数参数估计的方法多为传统的数学估计方法,多数研究认为,最大似然估计(Maximum Likelihood estimation,MLE) 求的参数最优[6-7]。但最大似然估计要用迭代法求解,过程复杂。此外,由于3参数Weibull分布不能满足通常的正则条件,导致有时最大似然估计不存在或有多个解[8]。为解决这些问题,研究基于Weibull分布3参数的人工神经网络估计模型[9-10],建立Weibull参数估计系统(Estimation System of Weibull Parameters,WPES),以寻求一种操作简单、快捷的方法估计Weibull分布参数。
1 材料与方法
1.1 材料来源
材料来源于贵州省安顺、龙里和开阳,考虑到林龄和地理位置对林分直径分布的影响,分别选择不同龄级(14,22和30 a)、不同密度级、不同地区的标准地调查数据来进行研究。贵州省气候为温凉湿润向半湿润过渡类型,年均气温为12~14℃,1月均温为2~4℃。≥10℃的积温约为4 000℃,生长期约为250 d,年降水量为1 000~1 200 mm,适于马尾松林分的生长。3块标准地的林分基本情况如表1。
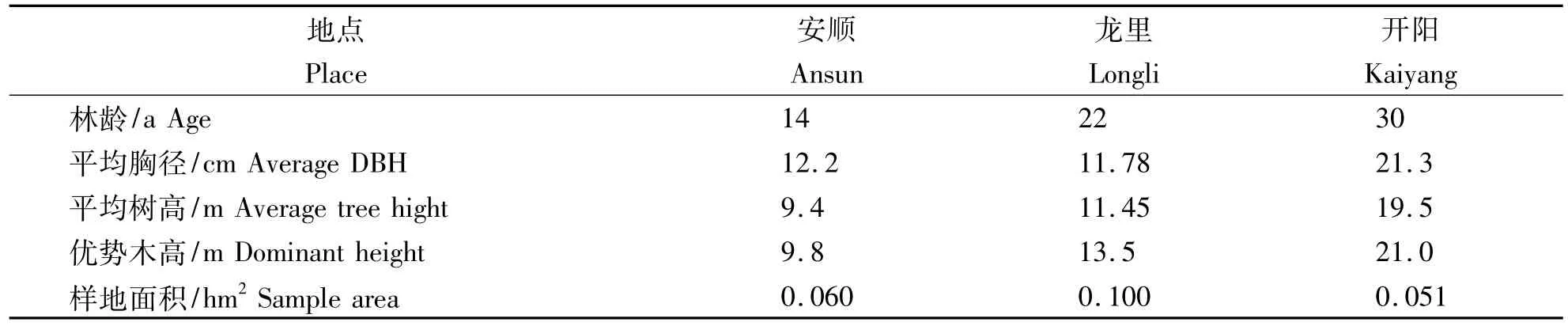
表1 标准地数据表Table 1 The data table of sample plot
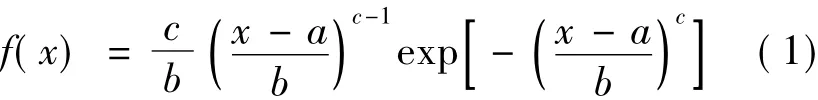
1.2 Weibull分布函数
Weibull分布函数的概率密度函数[4]:

式中:x为林木胸高直径;a为位置参数,这里为林分直径最小径阶下限值≥0;b为尺度参数;c为形状参数。
1.3 Weibull参数估计系统(WPES)
根据西泽正久相关表中120组c,Γ1,CVx的数值,用人工神经网络方法,以CVx作为输入向量,以c,Γ1作为输出向量,研究提出了由图1、式(3)~式(5)和表2组成的Weibull分布参数估计模型[9]。图1为估计模型的神经网络图形表达,其网络结构为1∶6∶2,即1个输入节,6个隐层神经元,2个输出神经元。
其数学模型为:
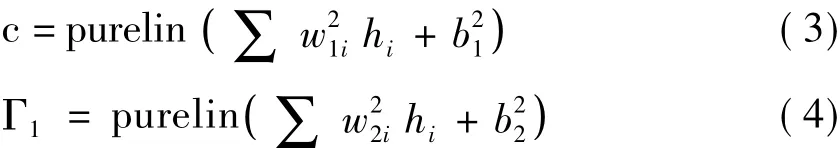
累积分布函数:

图1 神经网络模型(1∶6∶2)Fig.1 Neural network model(1∶6∶2)
式中:pure lin()和log sig()为MATLAB的神经元线性传递函数和对数S形传递函数;为从隐含层i节点至输出层节点的连接权;hi为隐含层i节点的输出值;为输出层节点的阈值;为从输入层节点至隐含层i节点的连接权;为隐含层i节点的阈值。

表2 神经网络模型输入层的权值和阈值Table 2 Weights and thresholds of neural network model
根据上述神经网络模型的输出和模拟对象的分布特征数,计算Weibull分布3参数:
1)用模拟对象的最小径阶中值(MD)减去径阶距(△D)的一半作为位置参数(a):

2)用式(4)计算位置尺度参数Γ 1 后,用Γ 1 除林分算术平均直径(Dm)与位置参数(a)的差作为
3)用式(3)计算形状参数c。
按上述模型或方法,可进行Weibull参数估计系统构建[12],通过MATLAB的GUI界面编辑器增加控件,构建系统界面如图2。根据系统可以直接输入各经阶中值和株数得到Weibull 3个参数。
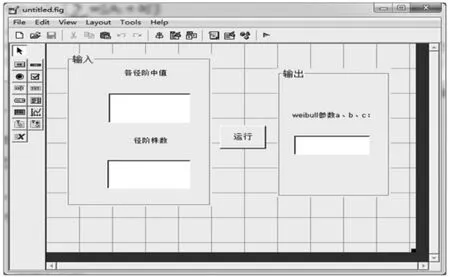
图2 Weibull参数预估系统界面Fig.2 The interface of estimation system for Weibull parameters
1.4 最大似然法(MLE)
本研究选择多数研究者认为最优的最大似然法(MLE)作对比分析。根据前人的研究[6-8],对于林分直径的Weibull分布,计算形状参数(c)的公式为:
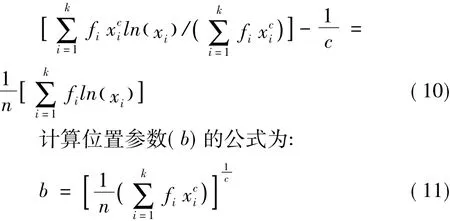
位置参数(a)算法同式(8)。
式中:k为径阶个数;xi为第i阶中值;fi为第i径
阶内林木株数;n为总株数。
1.5 拟合效果检验
用精度检验和χ2检验2种方法检验上述系统和方法估计的林分直径分布效果。精度算式:

式中:Pc为拟合精度;N为各径阶实测株数;N1为各径阶拟合株数;sum()和abs()为MATLAB的求和函数和绝对值函数。其中N1为:

式中:f(xi)为由式(1)求出的第i径阶中值为xi的概率密度函数值;△D为径阶距。
卡方检验(χ2)是关于理论频数与实际频数间吻合程度的一个检验方法[11]。卡方值算式:
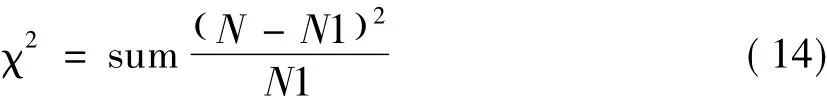
2 结果与分析
2.1 Weibull参数估计结果
利用构建的Weibull参数估计系统(WPES)可以直接计算Weibull参数值,如图3所示为安顺标准地的Weibull 3参数的计算结果。同理计算龙里、开阳标准地的结果,并与最大似然估计(MLE)的计算结果对照列如表3(WPES系统计算取了小数点后5位,为了与MLE方法统一起来,2种方法都取小数点后4位)。
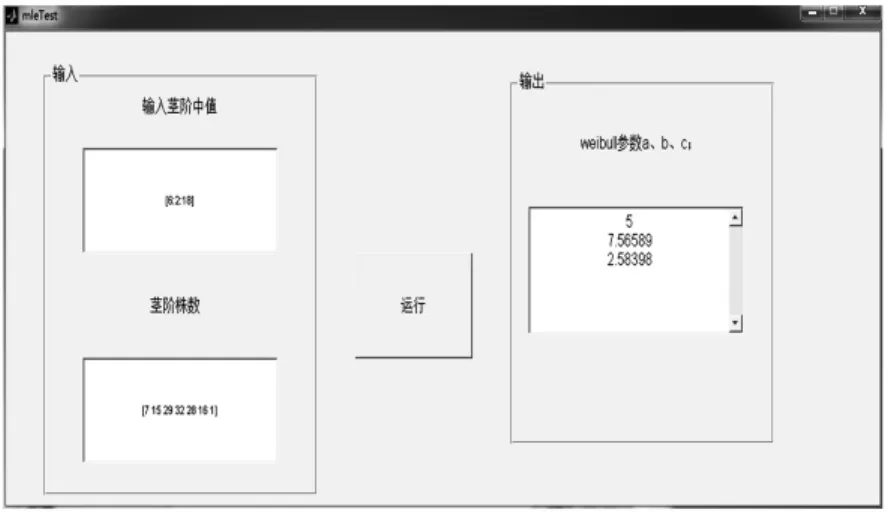
图3 安顺Weibull 3参数计算结果Fig.3 Weibull three parameter calculation results of Anshun
2.2 直径分布拟合结果
将表3中2种方法(WPES,MLE)估计的参数代入Weibull分布的概率密度函数式(1)和累积分布函数式(2),计算各标准地、各径阶的概率密度函数值和累积分布函数值,进而计算各径阶的拟合株数。计算结果与实测结果对照见表4。
由表4可知,用 WPES和 MLE估计并按式(12)计算的安顺、龙里、开阳3块标准地直径分布的拟合精度分别为84%、85%、85%和78%、64%、67%。显然,用WPES估计Weibull参数值的拟合精度比MLE的高,要高出5% ~20%。用WPES估计的各径阶拟合株数与实测株数相对吻合,而用MLE估计的相差较大。由表4还可以看出,在林龄为14 a的安顺标准地中,MLE的拟合精度相对比在林龄较大的龙里、开阳2块标准地上的拟合精度高,精度值从78%降到64%,相差10%以上;而WPES在不同年龄段的拟合都保持约85%的较高精度,相差仅1%。这说明,由于系统中人工神经网络的作用,WPES不仅具有较高的估计效果,而且具有较强的适应性。

表3 Weibull 3参数估计值Table 3 Estimated value of the three-parameter Weibull

表4 直径分布实测与拟合结果Table 4 Actual and Fitting Results for Diameter Distribution n
2.3 卡方检验
基于表4的径阶分布数据,用式(14)计算2种方法的χ2值,连同相关参数一并对照列如表5。
由表5可知,取α=0.05,安顺、龙里和开阳的自由度分别为6、8和9,WPES估计的检验χ2值分别为7.17、8.73 和2.40,而 MLE 估计的检验 χ2值分别为52.62、45.31 和 7.96。对照结果显示,安顺和龙里WPES检验值是MLE的1/7和1/6,这2块标准地用MLE方法估计的渐进显著性<0.05,拒绝原假设,说明不符合原来的分布;开阳标准地的检验值都相对较小,2种方法的渐进显著性都>0.05,说明2种方法得出的结果都是符合原分布的;研究表明,WPES有较强的适应性。

表5 χ2检验Table 5 Chi-square test
3 结论
以贵州不同林场、不同林龄的3块马尾松标准地林分直径分布数据为验证材料,基于Weibull参数的BP神经网络估计模型,用MATLAB的GUI界面编辑了一个3参数Weibull估计系统(WPES)。并与最大似然估计(MLE)作对比分析,对WPES的估计准确度、适应性等进行了验证研究,得出如下结论:
(1)WPES的拟合精度较高,比 MLE高出5%~20%。
(2)WPES对不同时间和空间的适应性较强,其变动幅度是MLE的1/10。
(3)WPES界面简单明了,操作方便,使用简捷,便于推广应用。
[1] 黄家荣,孟宪宇,关毓秀,等.马尾松人工林直径分布神经网络模型研究[J].北京林业大学学报,2006,28(1):28-31.
[2] 铁牛.长白落叶松人工林林分直径分布研究[J].林业资源管理,2014(6):95-98.
[3] 张文,高天雷.马尾松林分直径结构研究[J].四川林勘设计,2001(2):26-30.
[4] 孟宪宇.使用Weibull分布对人工油松林直径分布的研究[J].北京林学院学报,1985(1):30-40.
[5] DIAMANTOPOULOU M J,OZCELIK R,CRECENTECAMPO F,et al.Estimation of Weibull function parameters for modelling tree diameter distribution using least squares and artificial neural networks methods[J].Biosystem Engineering,2015,133(2):33-45.
[6] 尹铭昕.内蒙古地区天然白桦林直径分布的研究[D].哈尔滨:东北林业大学,2014.
[7] 杨谋存,聂宏.三参数Weibull分布参数的极大似然估计数值解法[J].南京航空航天大学学报,2007,39(1):22-25.
[8] 郑荣跃,严剑松.威布尔分布参数估计新方法研究[J].机械强度,2002,24(4):599 -601.
[9] 黄家荣,任谊群,高光芹,等.森林生长的人工神经网络建模[M].北京:中国林业出社,2006.
[10] ABBASI B,RABELO L,HOSSEINKOUCHACK M.Estimating parameters of the three-parameter Weibull distribution using a neural network[J].European Journal of Industrial Engineering,2008,2(4):428 -445.
[11]洪伟.试验设计与统计分析[M].北京:中国农业出版社,2007.
[12]黄旭光,胡宇宸,黄家荣,等.基于人工神经网络对天然栎树生长动态模拟系统的研究[J].河南农业大学学报,2013,47(5):552 -556;561.

