Birkhoff系统的Noether-Mei对称性与守恒量*

王雪萍，张 毅

(1.苏州科技大学数理学院，江苏 苏州215009；2.苏州科技大学土木工程学院，江苏 苏州215011)

Birkhoff系统的Noether-Mei对称性与守恒量*

王雪萍1，张 毅2

(1.苏州科技大学数理学院，江苏 苏州215009；2.苏州科技大学土木工程学院，江苏 苏州215011)

研究Birkhoff系统Noether-Mei对称性与守恒量。给出Birkhoff系统Noether-Mei对称性的定义和判据，研究了Birkhoff系统的Noether-Mei对称性导致的Noether守恒量和Mei守恒量的条件及其形式，建立了两个Noether-Mei对称性定理，并举例说明结果的应用。

Birkhoff系统；Noether-Mei对称性；Noether守恒量；Mei守恒量

动力学系统的对称性与守恒量的研究具有重要意义, 在现代数学、力学、物理学中占有重要的地位, 也是分析力学的一个近代发展方向。对称性主要有：Noether 对称性，Lie对称性和Mei对称性[1-5]。随着研究的深入，人们对两种以上的对称性进行综合研究，并已取得一些成果[6-13]。本文将研究Birkhoff系统Noether-Mei对称性与守恒量，

给出系统Noether-Mei对称性定义和判据，研究Noether-Mei对称性与Noether守恒量和Mei守恒量之间的关系，建立了两个Noether-Mei对称性定理，并给出算例以说明结果的应用。

1 Birkhoff系统的Noether-Mei对称性

Birkhoff系统的运动微分方程为[1]

(1)

其中Rμ=Rμ(t,a)为Birkhoff函数组，B=B(t,a)为Birkhoff函数，且

(2)

称为Birkhoff系统的张量。设系统非奇异，即有det(Ωμν)≠0，由(1)解得

(3)

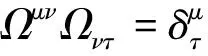
定义1 对于Birkhoff系统(1)，如果一个对称性既是其Noether对称性又是其Mei对称性，则称这个对称性为该系统的Noether-Mei对称性。

取变量aμ和时间t的无限小变换

(4)

其中ε为无限小参数，ξ0，ξμ为无限小变换的生成元。

(5)

其中

(6)

如果无限小变换(4)的生成元ξ0，ξμ满足方程

(7)

则相应对称性为Birkhoff系统的Mei对称性；如果存在规范函数GN=GN(t,a)，使无限小生成元ξ0，ξμ满足Noether等式

(8)

则相应对称性为Birkhoff系统的Noether对称性。于是有

判据1 如果存在规范函数GN=GN(t,a)，使无限小变换的生成元ξ0,ξμ满足方程

(9)

则相应对称性为Birkhoff系统的Noether-Mei对称性。

2 Noether-Mei对称性导致的守恒量

定理1 对于Birkhoff系统(1)，如果无限小生成元ξ0，ξμ满足Noether等式(8)，或使广义Killing方程

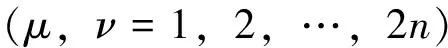
(10)

(11)

有解，则系统的Noether-Mei对称性导致Noether守恒量

(12)

定理2 对于Birkhoff系统(1)，如果无限小生成元ξ0，ξμ和规范函数GM=GM(t,a)满足结构方程

(13)

则系统的Noether-Mei对称性导致Mei守恒量

X(0)(B)ξ0+GM=const

(14)

其中

(15)

3 算 例

例 已知四阶Birkhoff系统的Birkhoff函数为[1-2]

(16)

Birkhoff函数组为

R1=a3，R2=a4,R3=R4=0

(17)

试研究系统的Noether-Mei对称性与守恒量。

方程(3)给出

(18)

做计算，有

(19)

Mei对称性的确定方程(7)给出

(20)

方程(20)有解

(21)

生成元(21)相应于系统的Mei对称性。

Noether等式(8)给出

(22)

将生成元(21)代入式(22)，得到

GN=0

(23)

生成元(21)亦相应于系统的Noether对称性。因此，生成元(21)是这个四阶Birkhoff系统的Noether-Mei对称性。

与生成元(21)相应的Mei对称性的结构方程为

(24)

其中

(25)

方程(24)有解

GM=0

(26)

由定理2，系统存在守恒量

IM=-2a3=const

(27)

式(27)是由系统的Noether-Mei对称性(21)导致的Mei守恒量。

将生成元(21)和规范函数(23)代入式(12)，得

IN=a3+a4(a3)2=const

(28)

由定理1，式(28)是系统的Noether-Mei对称性(21)导致的Noether守恒量。

4 结 语

研究了Birkhoff系统的Noether-Mei对称性，这种对称性既是系统的Noether对称性又是系统的Mei对称性，既能导致Noether守恒量又能在一定条件下导致Mei守恒量。主要结果为文中给出的由Birkhoff系统的Noether-Mei对称性导致Noether守恒量和Mei守恒量的两个定理。文章方法和结果具有普遍意义，可以推广到其他类型的约束力学系统。

[1] 梅凤翔. 李群和李代数对约束力学系统的应用[M]. 北京: 科学出版社, 1999.

[2] 梅凤翔. 约束力学系统的对称性与守恒量[M]. 北京: 北京理工大学出版社, 2004.

[3] 王树勇,梅凤翔.相空间中完整约束系统的形式不变性[J]. 中山大学学报(自然科学版), 2002, 41(6): 10-13.

[4] 张毅. 相空间中类分数阶变分问题的Noether对称性与守恒量[J]. 中山大学学报(自然科学版), 2013, 52(4): 45-50.

[5] 何胜鑫, 朱建青. 基于分数阶模型的相空间中非保守力学系统的Noether准对称性[J]. 中山大学学报(自然科学版), 2015, 54(4): 37-42.

[6] FANG J H, WANG P， DING N. Noether-Mei symmetry of mechanical system in phase space [J]. Commun Theor Phys, 2006, 45(5): 882-884.

[7] 方建会, 丁宁, 王鹏. 非完整力学系统的Noether-Lie对称性[J]. 物理学报, 2006, 55(8): 3817-3820 .

[8] 刘仰魁, 方建会. 相空间中变质量力学系统Lie-Mei对称性的两个守恒量[J]. 物理学报, 2008, 57(11): 6699-6703.

[9] LIU Y K, FANG J H, PANG T，et al. New conserved quantities of Noether-Mei symmetry for nonholonomic mechanical system [J]. Commun Theor Phys, 2008, 50(3): 603-606.

[10] ZHANG M J, FANG J H, LU K. Perturbation to Noether-Mei symmetry and adiabatic invariants for nonholonomic mechanical systems in phase space [J]. Commun Theor Phys, 2009, 51(4): 600-604.

[11] FANG J H, LIU Y K, ZHANG X N. New conserved quantities of Noether-Mei symmetry of mechanical system in phase space[J]. Chin Phys B, 2008, 17(6): 1962-1966.

[12] 徐超, 李元成. 奇异Chetaev型非完整系统Nielsen方程的Lie-Mei对称性与守恒量[J]. 物理学报, 2013, 62(12): 120201.

[13] 王延志, 孙现亭, 贾利群. 非完整力学系统Hamilton方程的Noether-Mei对称性与守恒量[J]. 江南大学学报(自然科学版), 2014, 13(5): 607-610.

Noether-Mei symmetry and conserved quantity of Birkhoffian system

WANGXueping1,ZHANGYi2

(1. College of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China;2. College of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, China)

The Noether-Mei symmetry and the conserved quantity of a Birkhoffian system are studied. The definition and the criteria of the Noether-Mei symmetry of the system are given. The conditions that the Noether-Mei symmetry leads to the Noether conserved quantity or the Mei conserved quantity and the form of the conserved quantities are obtained. Two theorems for the Noether-Mei symmetry and the conserved quantity are established. At the end, an example is given to illustrate the application of the results.

Birkhoffian system; Noether-Mei symmetry; Noether conserved quantity; Mei conserved quantity

10.13471/j.cnki.acta.snus.2016.04.009

2015-10-17

国家自然科学基金资助项目(11272227,11572212)；苏州科技大学研究生科研创新计划资助项目(SKCX15_062)

王雪萍(1989年生)，女；研究方向：力学中的数学方法；通讯作者：张毅;E-mail:zhy@mail.usts.edu.cn

O

A

0529-6579(2016)04-0053-03