切入式外圆磨削接触刚度与固有频率研究

迟玉伦　李郝林

上海理工大学，上海，200093



切入式外圆磨削接触刚度与固有频率研究

迟玉伦李郝林

上海理工大学，上海，200093

摘要：基于外圆切入磨削系统动力学简化模型，对磨削材料去除率模型的时间常数进行研究，提出了切入式外圆磨削接触刚度的有效测量方法，并建立了磨削接触刚度与系统固有频率的关系模型。通过大量磨削实验，验证了不同磨削工艺参数与接触刚度、系统固有频率及颤振频率的变化规律。研究结果为后续避免或抑制磨削颤振以及磨削工艺参数优化研究提供了实验基础和理论依据。

关键词：外圆切入磨削；接触刚度；动力学模型；颤振频率

0引言

磨削颤振是机床磨削系统加工过程中的一种动态不稳定现象，与磨床的动态性能、磨削工艺参数有着密切关系[1-3]。研究表明,系统的颤振频率与其固有频率有关，一般略高于固有频率[4]。砂轮与工件之间的接触刚度是影响颤振频率的一个重要参数，接触刚度大小不仅影响磨削加工尺寸精度及表面粗糙度，也是建立磨削动力学模型的基础。磨削过程中接触刚度的非线性变化特征，使磨削动力学系统成为一个非线性系统[5]，因此，有必要对外圆切入磨削工艺参数与接触刚度及系统固有频率的关系进行研究。

磨削接触刚度是指加工过程中磨削力与砂轮和工件之间接触变形之比，通常包括砂轮接触刚度和工件接触刚度两部分[6]。磨削过程中的接触变形无法直接测量，磨削接触刚度通常难以准确获得。Ramos等[7]利用测力环传感器进行机床静刚度测量实验，利用位移传感器测量磨削工件尾架顶尖变形来确定磨削接触刚度，该方法无法直接获得磨削力，难以获得较为准确的接触刚度绝对值。根据外圆切入式磨削加工过程，本文基于外圆切入磨削系统动力学简化模型，对磨削材料去除率模型[8]的时间常数进行研究，提出了切入式外圆磨削接触刚度的有效测量方法，并建立了磨削接触刚度与系统固有频率及颤振频率的变化模型，最后，通过实验验证了该方法的有效性和实用性。

1外圆切入式磨削系统动力学模型

砂轮与工件之间的接触刚度是磨削动力学系统中的一个可变的非线性参数[5]。下面对接触刚度确定方法进行研究，并探讨接触刚度变化对磨削动力学系统固有频率的影响。

1.1磨削接触刚度确定方法

基于磨削材料去除率模型中的时间常数对磨削接触刚度进行求解。磨削过程中产生的切削力使机床、砂轮和工件发生了弹性变形和较大的位移。如图1所示，外圆切入磨削力模型可以简化成含有三个弹簧的系统。

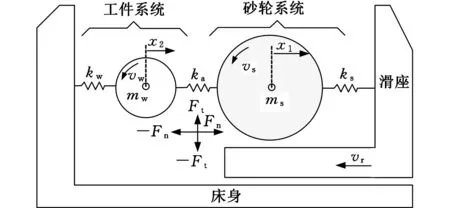
图1　磨削过程的系统简化模型

图1所示系统的等效刚度ke的计算公式为[9]

(1)

式中，ks为砂轮刚度；kw为工件刚度；ka为砂轮与工件之间的接触刚度；km为机床刚度(包括砂轮主轴刚度和工件刚度)。

磨削材料去除率模型中时间常数τ的表达式[10]如下：

(2)

式中，nw为工件转速；kc为磨削力系数。

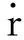
(3)

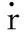
根据Alex等[11]的研究，根据稳定阶段的磨削力信号及磨削力信号变化率可计算出时间常数τ：

(4)

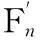
根据式(1)～式(4)可以得出磨削接触刚度ka，即

(5)

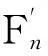
1.2磨削系统动力学模型

磨削系统的颤振频率与其固有频率有关，一般略高于系统的固有频率，因此研究接触刚度对磨削系统颤振频率的影响，可以转化为研究接触刚度对磨削系统固有频率的影响[12]。

根据外圆切入式磨削原理(图1)，可建立ms、mw的运动微分方程：

(6)

式中，ms为砂轮和主轴的质量；mw为工件质量。

将式(6)表示成矩阵的形式，即

(7)

其中，质量矩阵M和刚度矩阵K分别为

(8)

(9)

(10)

磨削系统的振动特征值问题可为

Ku=λMu

(11)

其中，λ=ω2，ω=2πf，ω为固有圆频率[13]，f为固有频率；u为模态向量。

系统中，除工件的质量m与接触刚度ka为变量外，其他均为常量，而对于同一工件来说，ka是系统中的唯一变量。由于ka随径向磨削力呈非线性变化，因此系统动态特性亦将发生变化。

采用一阶矩阵摄动法求解式(11)，令

(12)

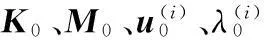
根据式(12)，经整理后可获得系统的固有频率：

(13)

由式(13)可以看出，磨削系统固有频率的变化与刚度矩阵的变化有关，而刚度矩阵变化主要来自接触刚度kc的变化。

2实验研究

为研究上述接触刚度对磨削系统固有频率的影响，通过相关实验设计对上述理论方法进行研究。

2.1机床静刚度测量

实验机床为德国斯莱福临公司STUDER K-C33精密外圆磨床，机床主轴转速为1～1500 r/min，最小进给量为0.1 μm；砂轮型号为53A80L15V，宽度为62 mm，直径为440 mm；工件材料为45钢，直径为50 mm。磨削时砂轮线速度为35 m/s，工件转速为120 r/min。磨削冷却液为嘉实多Hysol R 水基磨削液。如图2所示，力传感器的型号为Kistler公司的9323A，测量范围为0～1 kN，灵敏度为-9.6 pC/N；位移传感器采用非接触式电涡流位移传感器，其型号为MICRO-EPSILON eddyNCDT 3010，量程为1 mm，分辨能力为0.05 μm，具有较好抗干扰性能。

(a)机床静刚度测量原理

(b)机床静刚度实测图图2　机床静刚度测量实验

如图2所示，将压力传感器安装在砂轮与工件之间，用以测量砂轮与工件的压力；将位移传感器安装于工件一侧(测点1)，用以测量工件的变形量。设定机床程序，使用手轮控制机床以较低速度使砂轮挤压力传感器，在此过程中，记录位移传感器的测量变形值Δm和压力传感器的变化值ΔFm，可计算出工件静刚度kw；再将位移传感器安装于砂轮一侧(测点2)，以测量砂轮的变形量，用上述类似方法可计算出砂轮静刚度ks。由此可获得机床静刚度km：

(14)

根据上述测量方法，获得该机床静刚度km为6.15 MN/m。

2.2磨削力测量

为测量外圆切入磨削力，使用旋转轴力传感器，该传感器由转子(力传感器)和定子(信号处理器)两部分组成，如图3所示。通过专用夹具将传感器转子部分安装于机床头架主轴上，并随头架主轴一起转动，定子部分是以非接触方式与转子进行数据交互的。测量力传感器型号为Kistler 9123C，使用转速为1～10 000 r/min，灵敏度为2 mV/N，线性度小于±2%(满量程)，传感器自身固有频率为2.0 kHz，最大测量力量程为±50 kN。信号处理器型号为Kistler 5223B，有4个通道(X、Y、Z三个方向力信号及扭矩M)，每通道的最高采样频率为7.8 kHz，模拟量±10 V输出。

图3　磨削加工实验

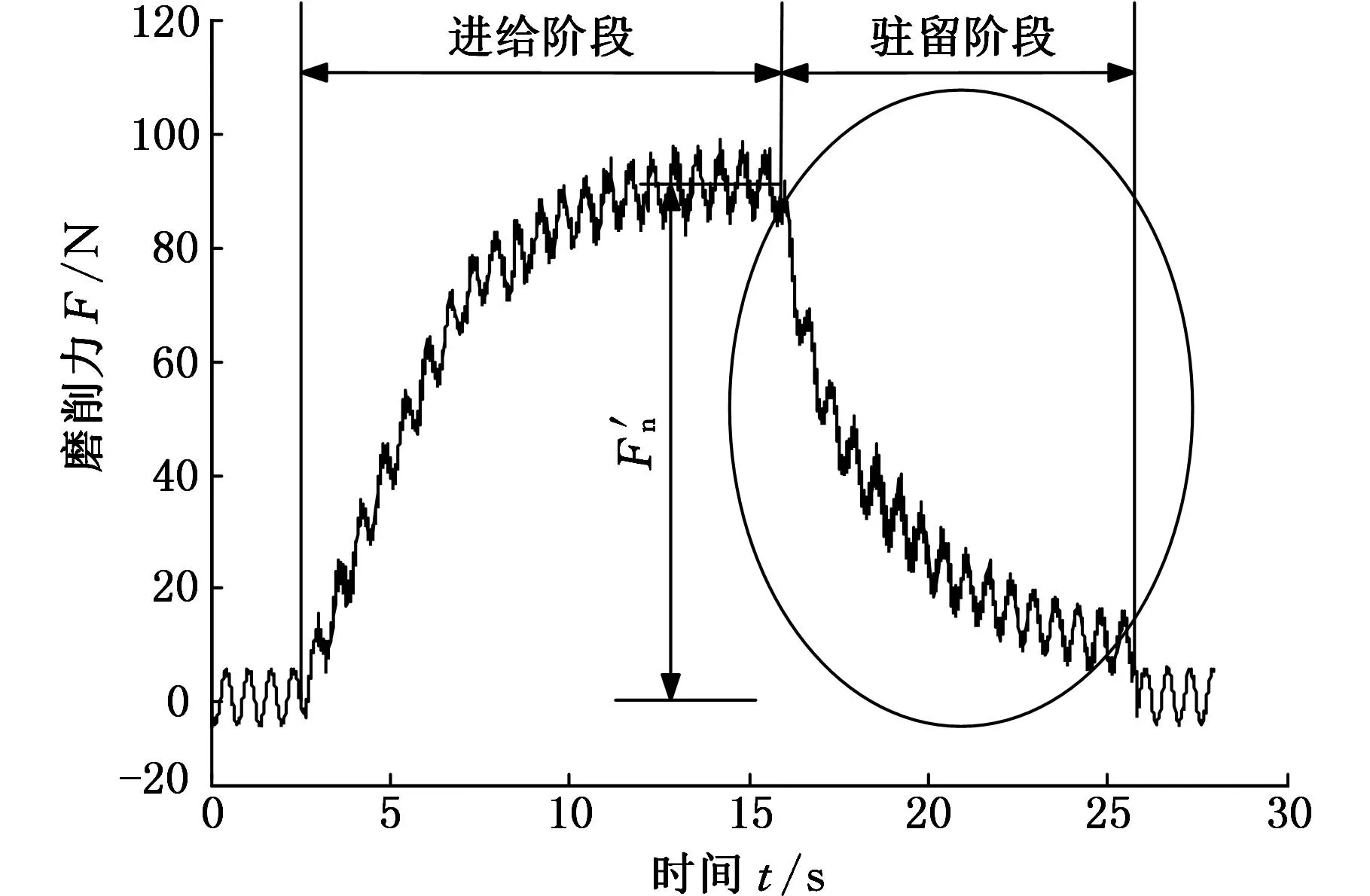
图4　磨削力信号

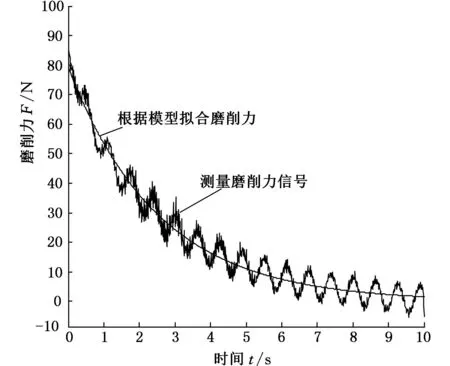
图5　驻留阶段磨削力信号拟合

2.3磨削接触刚度及系统固有频率计算分析

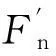
2.3.1不同进给速度的磨削接触刚度及系统固有频率

研究了不同进给速度对磨削接触刚度的影响，砂轮转速为35 m/s，工件转速为120 r/min，设计不同进给速度切入磨削实验，并分别计算其磨削接触刚度，结果如表1所示。

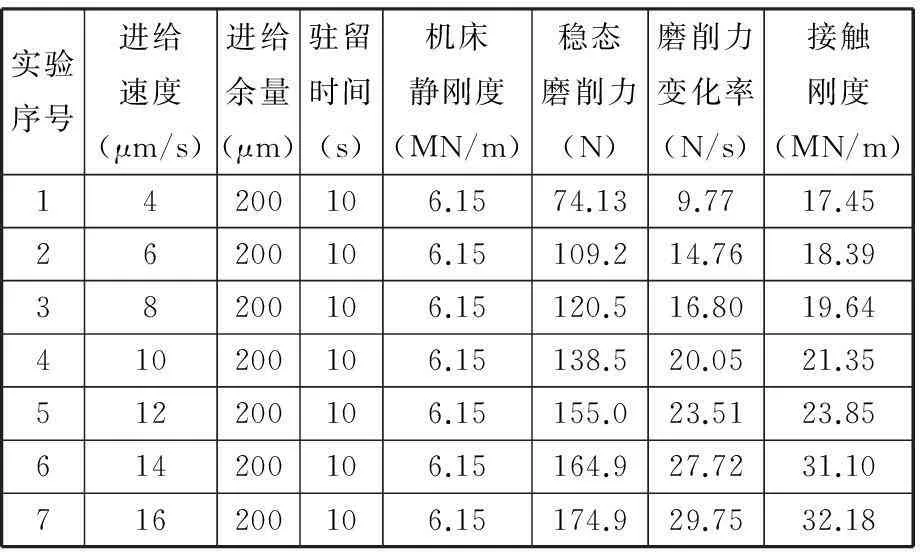
表1　不同进给速度的磨削接触刚度

如图6所示，稳态磨削力与磨削力变化率随着机床进给速度的增大而不断增大。

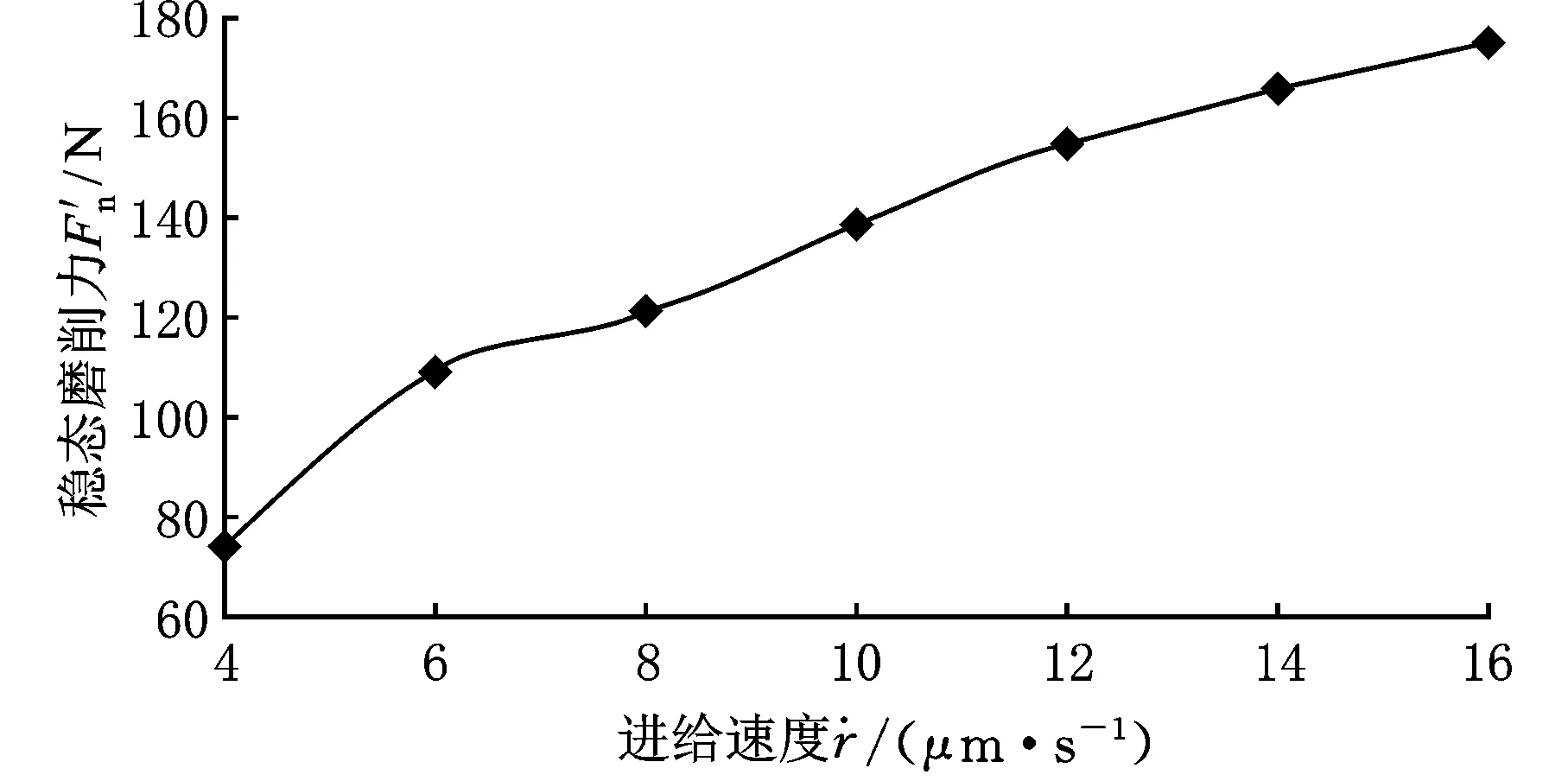
(a)稳态磨削力随进给速度变化关系

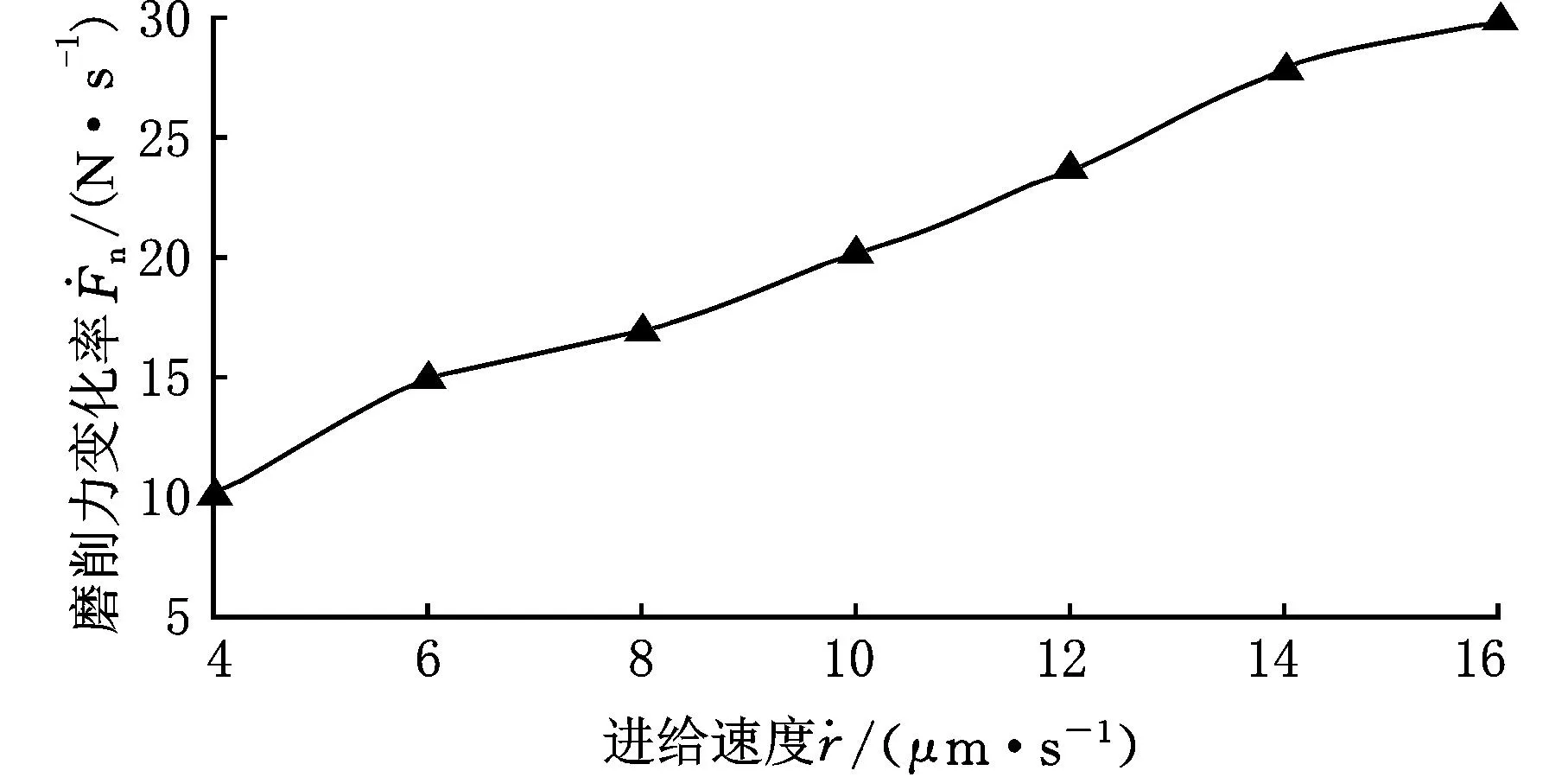
(b)磨削力变化率随进给速度关系图6　稳态磨削力与磨削力变化率随进给速度变化曲线

由图7a可看出，时间常数随着磨削进给速度的增大而减小。如图7b所示，在磨削力作用下，砂轮与工件接触区的磨粒发生刃口变形和中心变形；而随着磨削力(磨削深度)的增大，接触面的磨粒数将增加，即接触面亦增大，导致接触变形的增大趋势逐渐缓慢，从而使砂轮的接触刚度呈非线性增大。接触刚度与磨削力的关系可简化成

(15)

式中，h1为磨削力修整系数；q为法向磨削力函数；vs、vw分别为砂轮线速度和工件线速度。

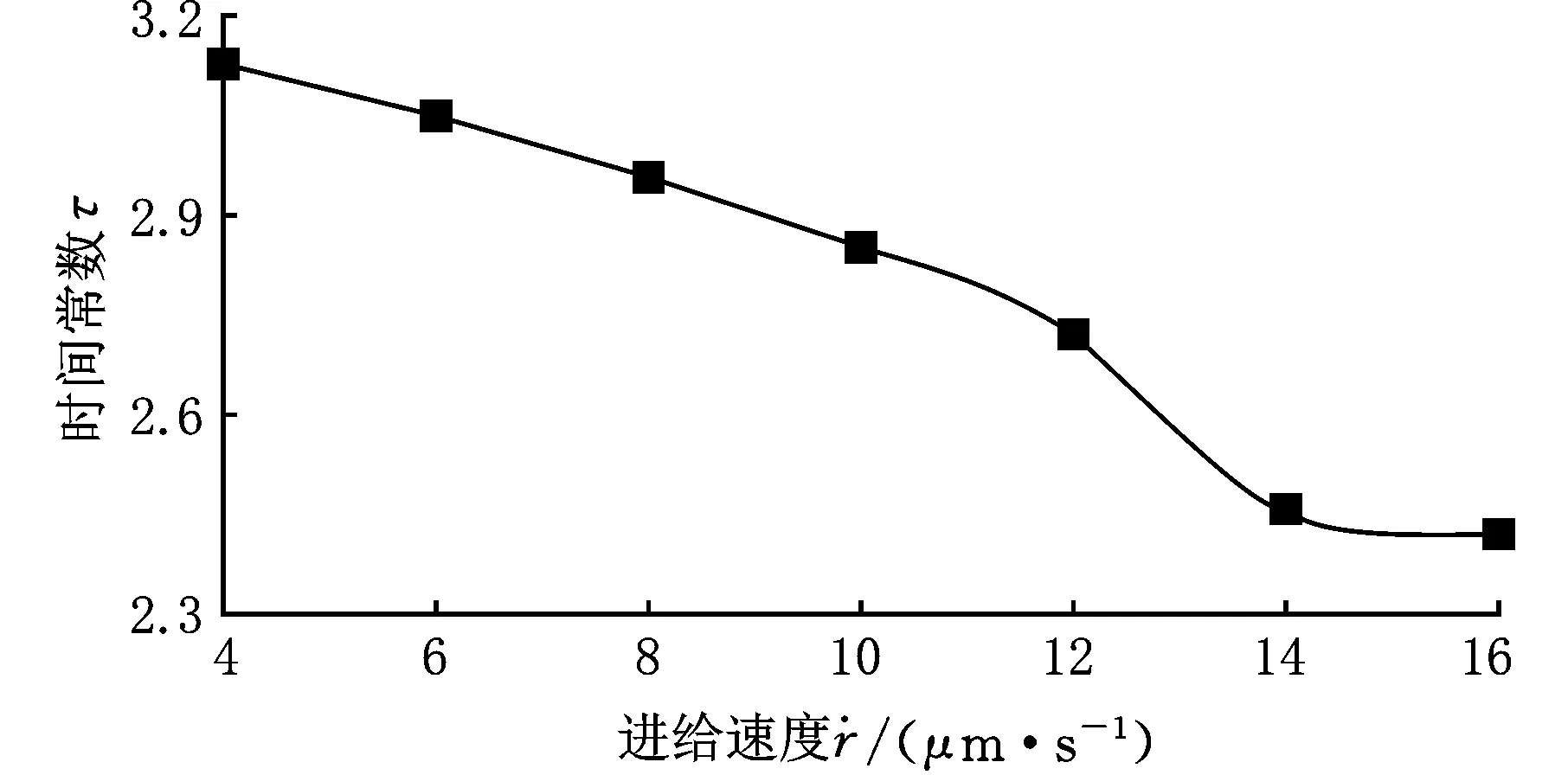
(a)时间常数随进给速度变化曲线

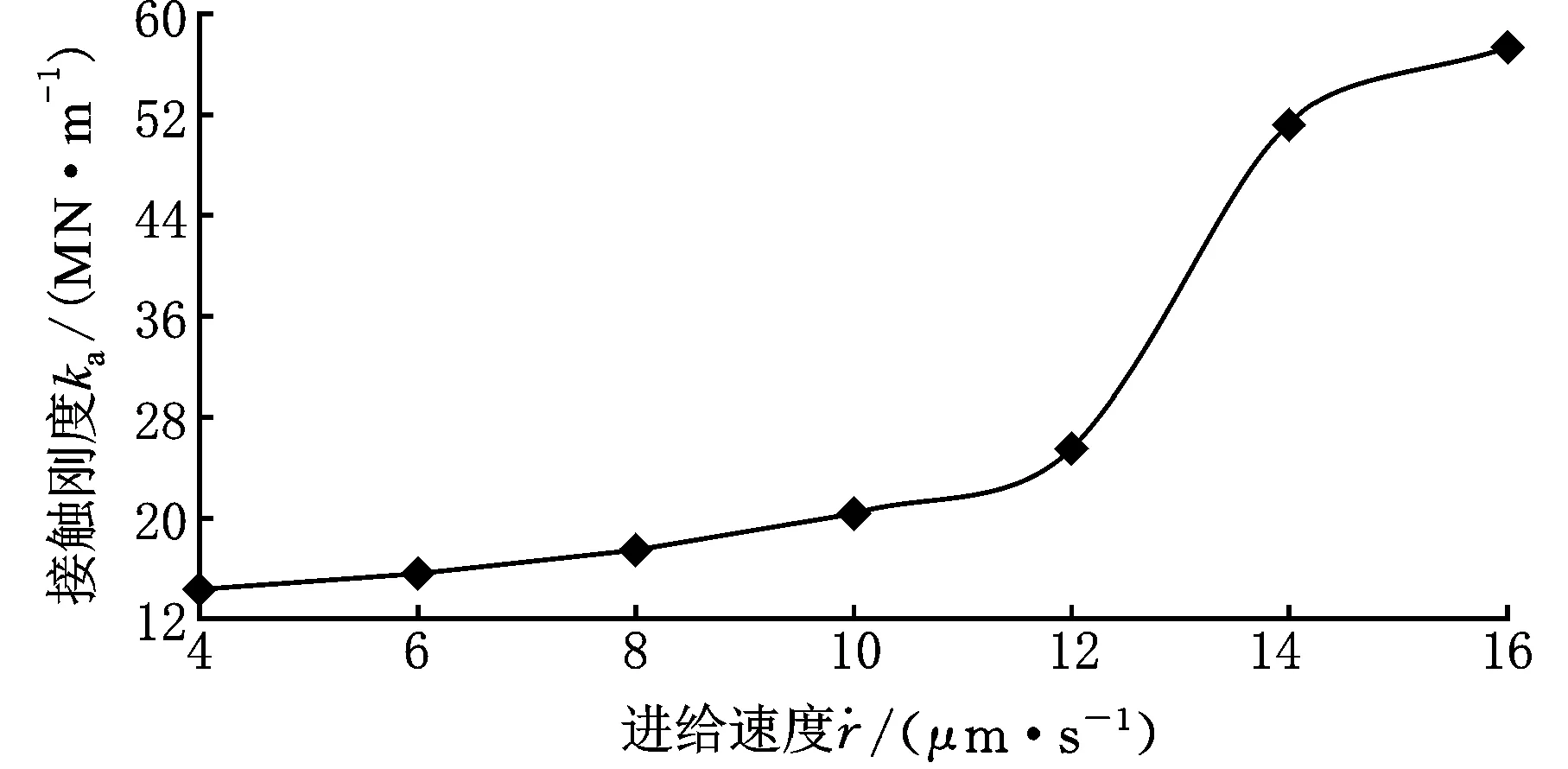
(b)接触刚度随进给速度变化曲线图7　时间常数与接触刚度随进给速度变化曲线

为计算磨削系统固有频率，首先对图1所示磨削系统中的工件和砂轮的相关参数进行测量，如表2所示，其中工件刚度kw和砂轮主轴刚度ks可由2.1节机床刚度实验获得。

表2　工件和砂轮参数表

将表1和表2参数值代入式(13)计算磨削系统固有频率与进给速度及接触刚度的关系，如图8所示。

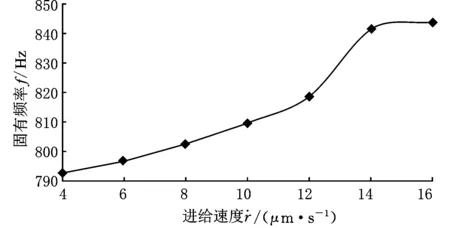
(a)固有频率与进给速度的关系曲线

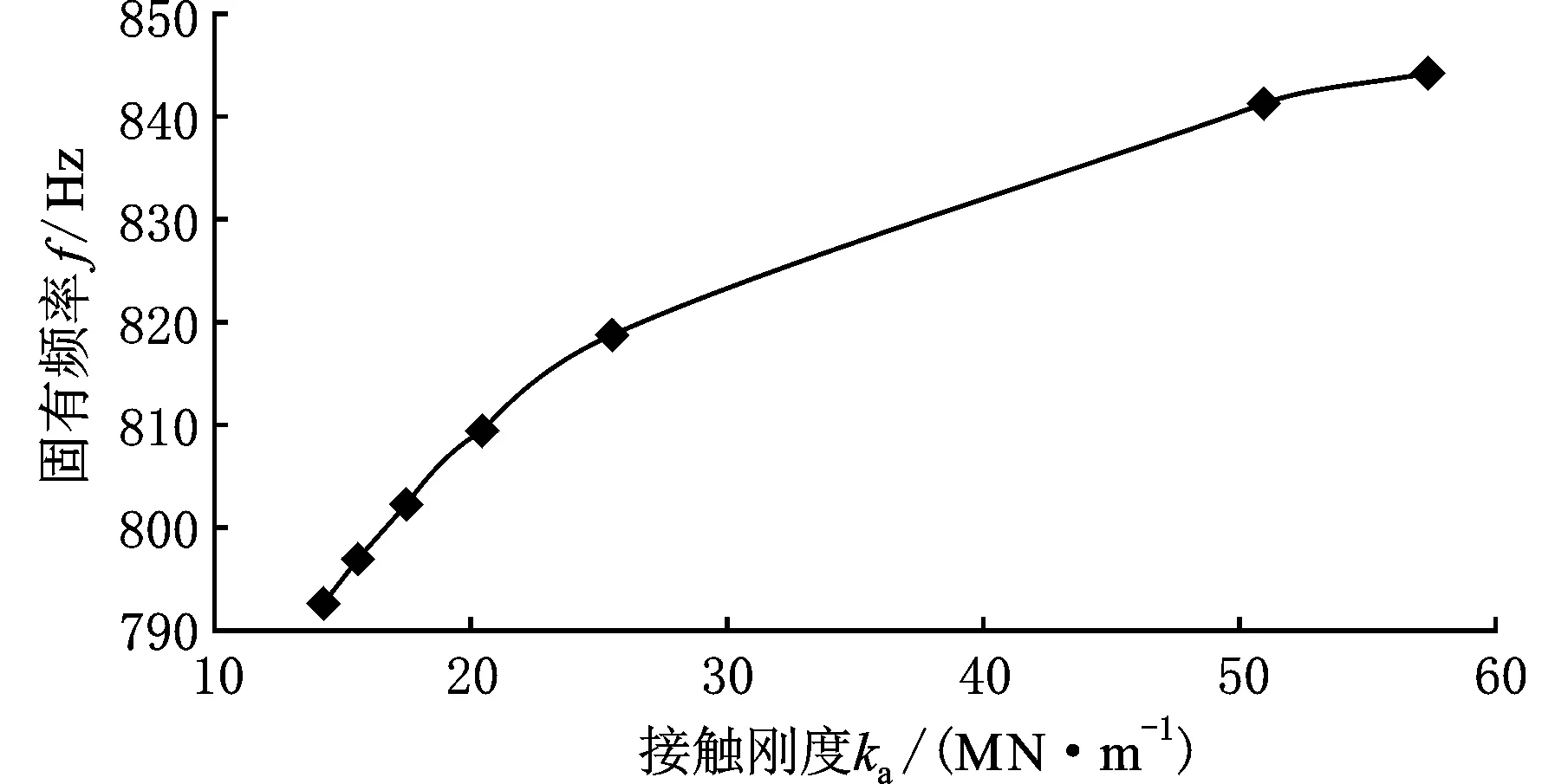
(b)固有频率与接触刚度的关系曲线图8　固有频率与进给速度及接触刚度变化曲线

如图8a所示，系统固有频率随着进给速度的增大而增大，说明系统固有频率与磨削接触刚度成一定的正比例关系(图8b)。为验证上述结果的准确性，将振动传感器安装于机床尾架顶尖处，如图3所示，对不同进给速度参数下的功率谱进行分析，运用贝叶斯理论和模态分析相结合的模态参数识别技术对机床系统固有频率进行识别[14](消除切削激励和随机激励的影响)，其测量结果固有频率也是逐渐增大的，从而验证了上述方法的有效性。

2.3.2不同砂轮速度和工件转速的系统固有频率

基于上述计算方法分别研究不同砂轮速度及不同工件转速对系统固有频率的影响，磨削进给速度为9 μm/s。

系统固有频率随着砂轮速度的增大先增大后逐渐减小，如图9a所示；而系统固有频率随着工件转速的增大逐渐减小，如图9b所示。

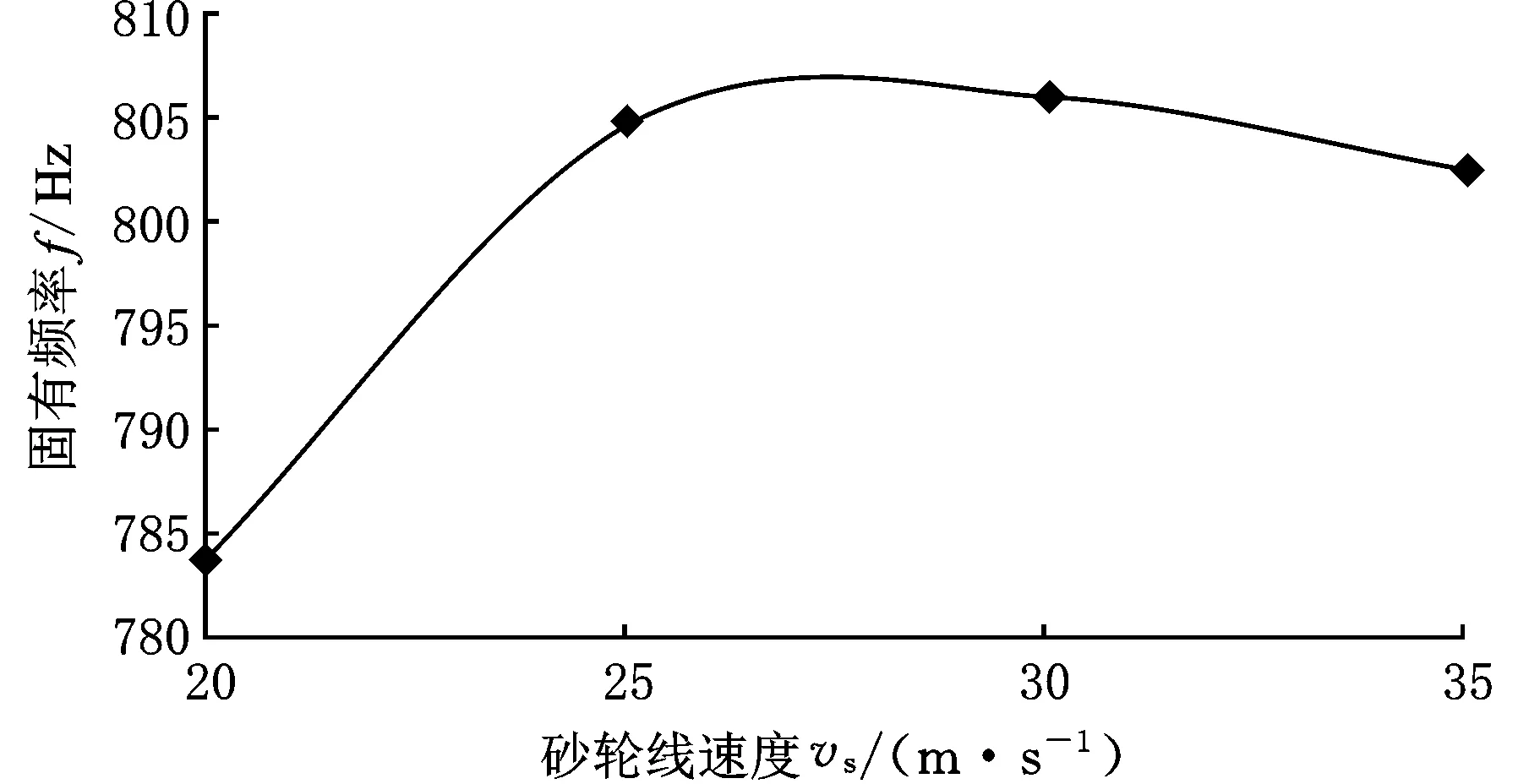
(a)固有频率与砂轮线速度关系曲线

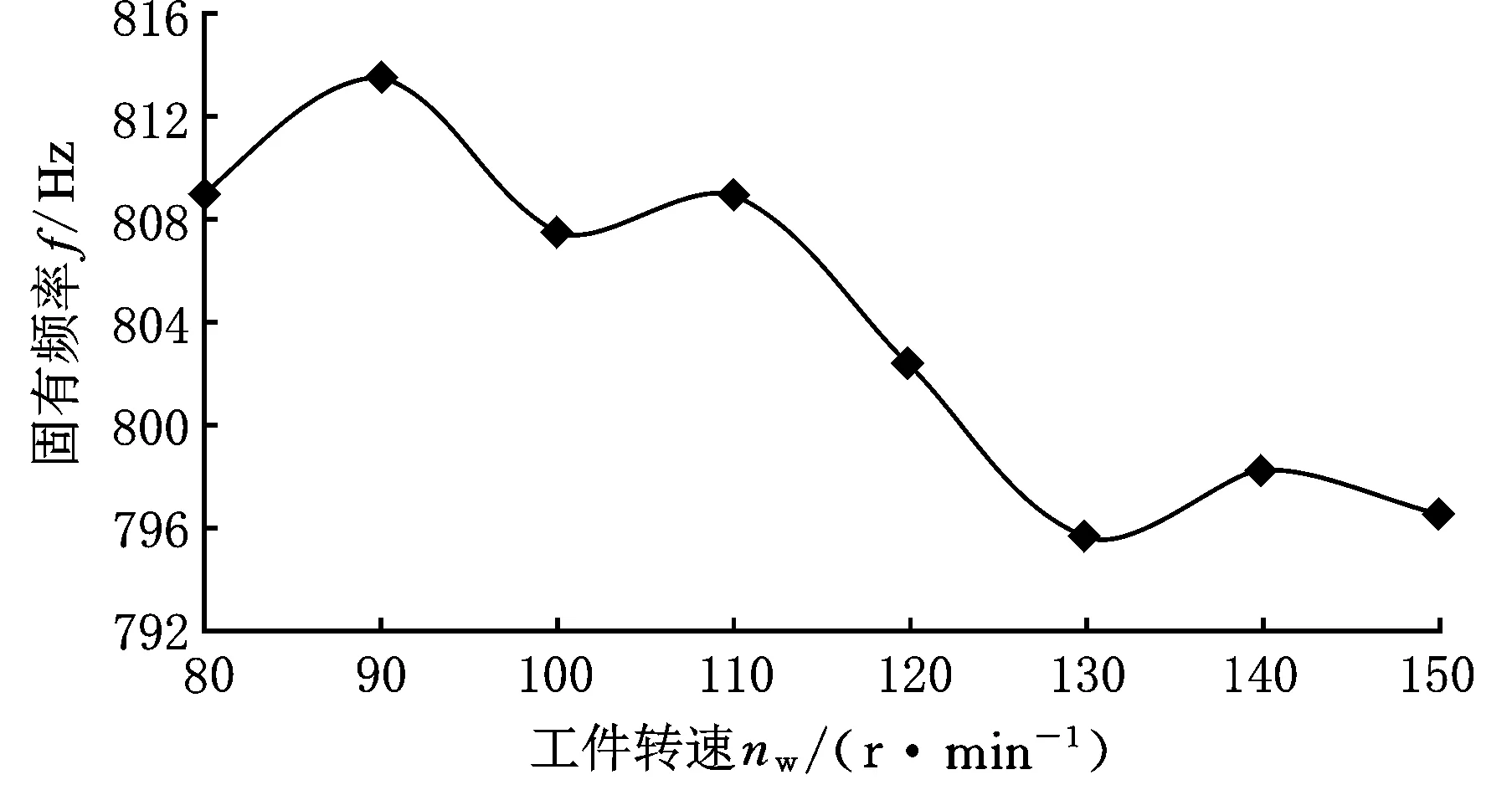
(b)固有频率与工件转速关系曲线图9　固有频率与砂轮速度及工件速度变化曲线

由上述实验不同进给速度计算结果(图8)可以得出，随着磨削进给速度的增大，磨削力逐渐变大，时间常数会逐渐变小，磨削接触刚度及系统固有频率逐渐增大；由图9可知，系统固有频率随着砂轮速度的增大先增大后逐渐减小，系统固有频率随着工件转速的增大而逐渐减小。由于系统的颤振频率与其固有频率有关，一般略高于固有频率，结合式(15)可知系统颤振频率与系统固有频率、接触刚度及工艺参数存在一定的关系，因此，在切入磨削加工过程中，通过调整工艺参数(砂轮转速、进给速度与工件转速等)可改变系统的接触刚度、固有频率及颤振频率。后续研究将建立接触刚度与系统颤振之间的关系模型，研究磨削工艺参数与接触刚度及系统颤振之间的关系。

3结论

(1)基于外圆切入磨削力学原理及磨削去除率模型，提出了一种利用时间常数与实验测量结果相结合的方法来准确确定磨削接触刚度，并建立磨削接触刚度与系统固有频率的动力学关系模型。

(2)设计了一套完整实验方案对机床静刚度进行测量，并将旋转轴力传感器安装在机床头架主轴上对磨削力进行测量，根据测量实验结果完成对磨削时间常数、接触刚度及系统固有频率的计算。

(3)根据上述实验计算结果分析，随着磨削工艺参数变化，磨削接触刚度及系统固有频率也会发生变化。由于系统的颤振频率略大于固有频率，所以颤振频率也随着接触刚度的增大而增大。通过调整磨削工艺参数(砂轮转速、进给速度与工件转速等)可改变系统颤振频率。

参考文献：

[1]LiH，ShinYC.AStudyonChatterBoundariesofCylindricalPlungeGrindingwithProcessCondition-dependentDynamics[J].InternationalJournalofMachineToolsandManufacture，2007,47(10):1563-1572.

[2]GagnolV,BouzgarrouBC,RayP.Model-basedChatterStabilityPredictionforHigh-speedSpindles[J].InternationalJournalofMachineToolsandManufacture,2007,47(7):1176-1186.

[3]MahnamaM,MovahhedyMR.PredictionofMachiningChatterBasedonFEMSimulationofChipFormationunderDynamicConditions[J].InternationalJournalofMachineTools&Manufacture, 2010,50:611-620.

[4]YaoZhehe,MeiDeqing,ChenZichen.On-lineChatterDetectionandIdentificationBasedonWaveletandSupportVectorMachine[J].JournalofMaterialsProcessingTechnology, 2010，201：713-719.

[5]王龙山，崔岸，于爱兵.砂轮与工件接触刚度对磨削颤振频率的影响. 吉林工业大学学报，1995, 25(4):26-32.

WangLongshan,CuiAn,YuAibing.TheInfluenceoftheContactStiffnessbetweenGrindingWheelandWorkpieceonGrindingChatterFrequency[J].JournalofJiLinUniversityofTechnology, 1995, 25(4):26-32.

[6]ShiauTN,HuangKH,WangFC,etal.DynamicResponseofaRotatingBallScrewSubjecttoaMovingRegenerativeForceinGrinding[J].AppliedMathematicalModelling, 2010,34:1721-1731.

[7]Ramos J C, Vinolas J, Nieto F J. A Simplified Methodology to Determine the Cutting Stiffness and the Contact Stiffness in the Plunge Grinding Process[J]. International Journal of Machine Tools & Manufacturing, 2001,41: 33-49.

[8]姜晨,李郝林.基于声发射信号的精密外圆切入磨削时间评估算法和试验研究[J].机械工程学报,2014,50(3);194-200.

Jiang Chen, Li Haolin. Algorithm and Experiment of Estimation of Time of Precision Cylindrical Plunge Grinding Based on Acoustic Emission Signal[J]. Journal of Mechanical Engineering, 2014,50(3):194-200.

[9]马尔金·S.磨削技术与理论[M].蔡光起,巩亚东,宋贵亮，译.沈阳：东北大学出版社，2002.

[10]Marsh E R, Moerlein A W, Deakyne T R S， et al. In-process Measurement of Form Error and Force in Cylindrical-plunge Grinding[J]. Precis. Eng., 2008,32:348-352.

[11]Alex W M,Erc R M,Theodore R S D. In-process Force Measurement for Diameter Control in Precision Cylindrical Grinding[J]. Int. J. Adv. Manuf. Technl., 2009,42:93-101.

[12]林洁琼，周晓勤，孔繁森,等.再生切削颤振系统动态响应谐参数辨识[J].吉林大学学报(工学版)，2009,39(4): 964-969.

Lin Jieqiong, Zhou Xiaoqin,Kong Fansen. Harmonic Parameter Identification of Dynamic Response in Regenerative Machining Chatter System[J]. Journal of Jilin University(Engineering and Technology Edition), 2009,39(4):964-969.

[13]蒋永翔，王太勇，黄国龙,等.外圆纵磨再生颤振稳定性理论及评价方法的研究[J]. 振动与冲击, 2008, 27(12):61-63.

Jiang Yongxiang, Wang Taiyong, Huang Guolong, et al. Theory of Regenerative Chatter Stability and Evaluation Method for Cylindrical Traverse Grinding[J]. Journal of Vibration and Shock, 2008,27(12):61-63.

[14]胡育佳,徐琳琳,李郝林.基于贝叶斯运行模态分析法的砂轮架动态特性分析[J].中国机械工程, 2014,25 (22):3081-3087.

Hu Yujia, Xu Linlin, Li Haolin. Dynamic Characteristics Analysis of Wheel head Based on Bayesian OMA Approach[J]. China Mechanical Engineering,2014,25(22):3081-3087.

(编辑苏卫国)

Study on Contact Stiffness and Natural Frequency in Cylindrical Plunge Grinding

Chi YulunLi Haolin

University of Shanghai for Science and Technology, Shanghai， 200093

Abstract:Based on the cylindrical plunge grinding system simplified dynamics model, a new method was provided to determine the contact stiffness accurately by using the time constant of material removal model. And, a dynamics model was established to analyze the relationship between the contact stiffness and the system natural frequency. At last, the changing rules of contact stiffness, system natural frequency (or chatter frequency) with different parameters were verified by experiments. The research results provide important experimental data and theoretic method for avoiding or controlling grinding chatters and optimizing the grinding parameters in future.

Key words:cylindrical plunge grinding; contact stiffness; dynamics model; chatter frequency

收稿日期：2015-07-07

基金项目：国家科技重大专项(2013ZX04008-011)

中图分类号：TG501

DOI：10.3969/j.issn.1004-132X.2016.10.003

作者简介：迟玉伦，男，1982年生。上海理工大学机械工程学院助教、博士研究生。研究方向为精密检测、现代制造技术。李郝林，男，1961年生。上海理工大学机械工程学院教授。