求解物流Web服务组合问题的两阶段多目标蚁群算法

方清华　倪丽萍　李一鸣

合肥工业大学，合肥，230009



求解物流Web服务组合问题的两阶段多目标蚁群算法

方清华倪丽萍李一鸣

合肥工业大学，合肥，230009

摘要：针对基于QoS的物流Web服务组合优化问题，提出了两阶段多目标蚁群优化(TMACO)算法。首先，针对原始数据集中存在被支配候选服务而增加算法求解时间的问题，提出了基于Pareto支配的预优化策略；其次，针对属性权重难以确定的问题，提出了不依赖权重的信息素更新策略和启发信息策略；最后，针对基础蚁群算法容易陷入局部最优的问题，提出了懒蚂蚁策略。实验结果表明，TMACO算法具有良好性能，相对于基础蚁群算法、利用解与理想解距离来更新信息素的改进蚁群算法、遗传算法以及用支配程度作为解的个体评价的改进遗传算法，TMACO算法有更高的寻优能力，能够找到更多更优的非劣解。

关键词：物流服务；蚁群算法；服务组合问题；Pareto最优解；多目标优化

0引言

近年来，云计算(cloud computing)、物联网(internet of things,IoT)迅速发展，受到越来越多学者的关注。云计算和物联网将人类社会、信息世界和现实世界更紧密地联系、整合在一起。基于服务的信息系统让现实世界和虚拟世界的界限变得越来越模糊，也为软件应用程序创新提供了肥沃的土壤[1]。在物流领域，云计算可以帮助我们在物流需求快速增长、动态多变的情况下，灵活地开发各类物流应用[2]。一个新的基于IT的物流服务模式由此诞生，即云物流服务模式。

云物流服务模式就是基于云计算，对物流服务进行服务供应和服务管理。云是一种部署在互联网上的虚拟资源库，用户通过付费得到资源的使用权。云物流服务模式可以对资源进行动态配置，以更好地满足用户的请求。物流服务涵盖了个人物流服务和综合物流服务[3]。目前，云物流服务模式在理论和实践上存在以下问题：①物流资源因地理分布不同而异，具有多变性、形态多样性和区域自治性，这使得云物流平台上的资源共享和资源管理比其他云计算平台更复杂、更困难。②物流平台上的物流Web服务具有分布不均的特性，每个抽象Web服务对应的具体Web服务数量庞大，导致要找到“最优”具体Web服务变得异常困难。此外，这些大量的具体Web服务中，可能有的服务是不可用或已失效的，需要运用基于信任的方法来解决这类问题[4]。基于上述问题，本文阐述了资源虚拟化和组合服务的概念，重点研究在可用具体Web服务集合中，快速找到最优的服务组合。目前主要运用智能优化算法来求解，如遗传算法(genetic algorithm，GA)[5-6]、粒子群算法(PSO)[7]、蚁群算法(ACO)[8-9]等。

刘磊等[5]提出了多目标遗传算法(SMOGA)，将个体的支配强度和被支配强度相结合进行个体评价，根据评价结果进行环境选择并生成个体的交叉概率，进而提出了结合局部搜索的个体变异策略。但其实验中问题的规模较小，新个体评价方法在算法中的效果较难验证。刘志中等[6]基于改进的遗传算法，将全局QoS(quanlity of service)约束分解成局部QoS约束，在物流服务流程执行过程中，依据当前情景信息，选出满足局部QoS约束的最优物流服务。将全局QoS约束分解成局部QoS约束可能会导致某些只有部分属性较差但整体属性较优的服务被过滤，且最后提供的结果可选项较少，较难满足用户变化的需求。张焕焕等[10]基于遗传算法的交叉变异思想，对社会认知算法中的模仿学习和观察学习过程进行改进，并应用在离散型物流Web服务优化组合问题中，通过实验证明改进算法具有较高寻优能力。Zhao等[11]将具有QoS全局最优Web服务选择的问题转化为QoS感知的多目标多选择Web服务组合优化问题，最终找到Pareto最优解。王秀亭等[8]把蚁群算法引入Web服务选择领域，将基于QoS的Web服务选择问题转化为最优路径选择问题，并给出蚁群算法求解Web服务组合问题的模型，测试了蚁群算法求解Web服务选择问题的有效性，但并未对基础蚁群算法进行改进。Wei等[9]阐述了解空间理想解的概念，并利用解与理想解的距离指导信息素的更新，验证了其改进算法能够在巨大搜索空间找到接近最优的解。像这样用距离评价一个解的方法更易于理解，有良好的可解释性。

许多研究仍无法避免算法初期由于缺乏对搜索空间的知识，求解速度较慢、属性权重难以确定以及算法容易陷入局部最优的问题。本文针对上述问题，提出相应的改进策略，提出两阶段多目标蚁群优化(two-stage multi-objective ant colony optimization,TMACO)算法，并研究如何在云物流服务模式下，运用TMACO算法更快地找到更多更优质的物流Web服务组合优化问题的非劣解。

1物流Web服务组合问题

物流资源的柔性和可扩展性是云物流服务模式的关键，因此，有效解决物流资源的表达和封装是物流资源虚拟化的两个重点，而服务组合在保证物流资源之间有效协作方面至关重要。

1.1资源虚拟化

虚拟化象征着计算资源的抽象化，是资源共享和动态分配的关键，其目的是为用户和基于异构、自治资源的应用提供异构统一的集成操作平台[12]。在物流领域，尤其在互联网环境下，资源虚拟化能够让用户更方便、更灵活地利用物流资源，包括物流设备和云物流计算机系统中的计算资源，它不仅能将物理资源抽象成统一的逻辑资源形式，还可以通过资源服务的组合，为用户提供更高效、创新的资源形式。资源的虚拟化主要有两个任务：一是通过分析物流资源的功能与特点，建立一个资源表达模型；二是通过运用Web服务技术构建服务描述的方法来封装服务的资源信息。

物流资源具有多样性、复杂性和动态性等特性，要建立统一的表达模型相对比较困难。由于物流服务的含义和惯用法不同于传统Web服务，因此Web服务相关的标准(如WSDL)不能直接应用于物流资源的表达和信息封装。物流资源的虚拟化框架如图1所示，该框架分为三层，即物理资源层、虚拟资源层和服务资源层[13]。

图1　物流资源的虚拟化框架

在物理资源层，通过使用物联网相关技术，如RFID、传感器和全球定位系统等，可以检测到分布式物流资源，并将它们整合到云物流系统中[14]。在虚拟资源层，基于对物流资源特点的分析，将物理资源抽象成逻辑资源，并以此建立资源的表达模型。物流资源在服务封装层被封装成服务。这样便能以管理服务的方式来管理物流资源。

1.1.1物流资源表述

物流资源是指物流服务过程中用以支持整个物流活动的各种元素，如设备资源、人力资源、服务资源、信息资源和财政资源等。

物流资源的表达模型如图2所示，该模型包括三个等级[13]：①物理资源，用以支持整个物流活动的各种资源；②资源的信息表示，如资源的总体特征、属性和状态等；③资源接口，如对资源的状态进行查询和更新。

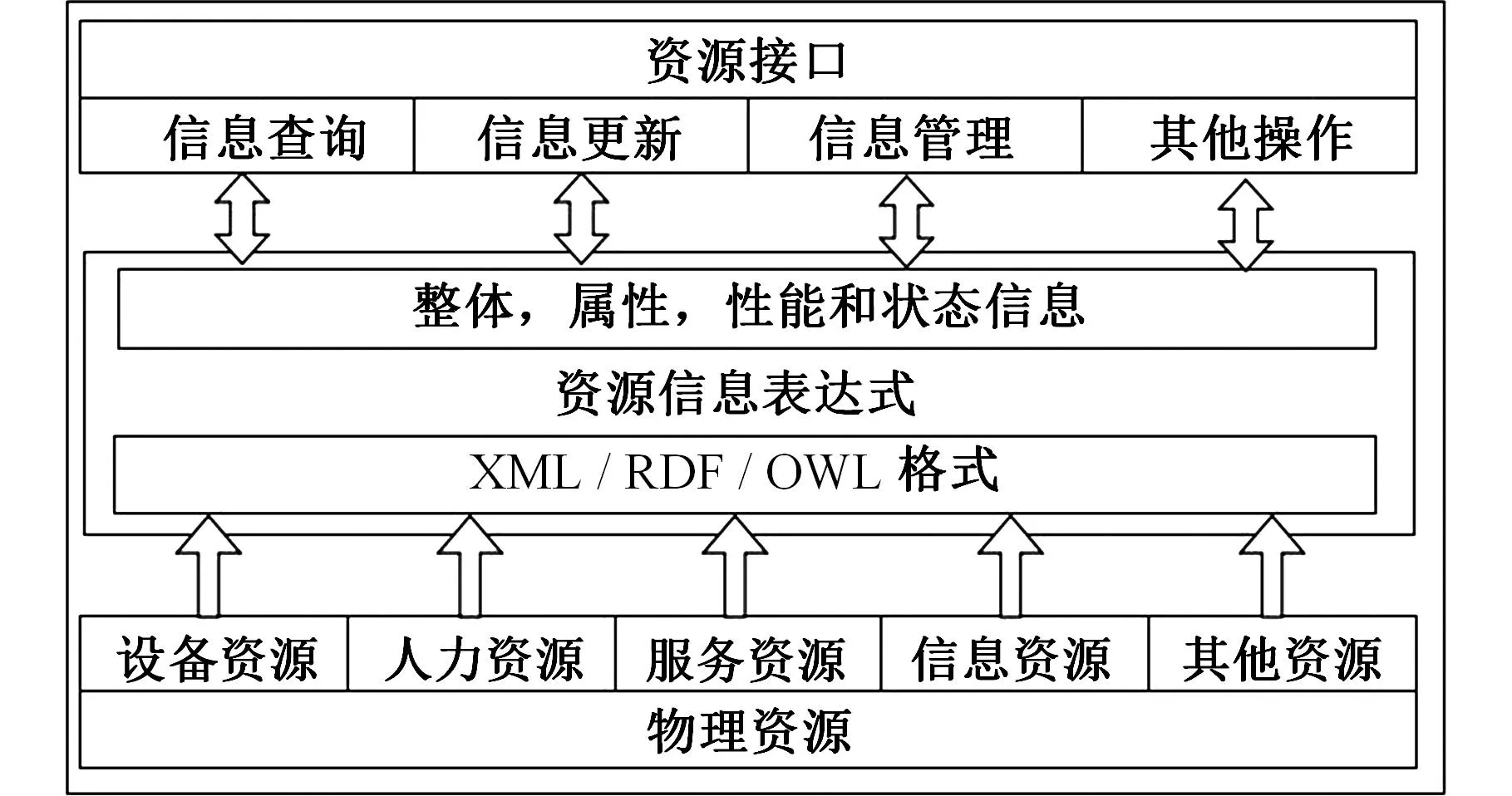
图2　物流资源表达模型

物流资源之间存在复杂的层级结构，为满足共享需求，需要用语义方法来描述物流资源之间的关系及其属性，以便规范它们在不同领域的表述，满足可扩展性，便于调整、修改，并扩展其分类和表述方法。

1.1.2物流资源封装

物流资源信息是从不同角度来描述的，我们着重关注位置、服务的功能和状态信息。资源的表达模式为LRE=〈LRid,LRpro,LRint〉。其中，LRid是物流资源在物理资源层的标识，它对用户透明，每个资源在全局空间有且只有一个通用资源标识符(URI)，它在一个特殊的命名空间中声明；LRpro表示虚拟资源层的物流资源信息，用XML语言来描述和封装；LRint定义的是使用Web服务描述语言(WSDL)在资源界面层进行的操作集合。

建立资源表达模型后，就可以在服务注册中心注册并发布物流服务。

1.2服务组合

服务组合就是要找到满足一些确定功能性需求和非功能性需求的适当的Web服务，将多个功能较单一的服务进行组合，构建成功能强大的组合服务来满足各种实际应用需求。

对服务组合的研究一般是基于QoS的服务组合进行的，Canfora等[15]已经证明基于QoS 的服务组合是NP难题。目前的研究主要是将服务组合问题视为优化问题，服务搜索过程中主要考虑服务的质量属性，求解过程主要运用智能优化算法。本文把服务组合问题看作多目标优化问题，并给出了蚁群算法求解基于QoS的服务组合问题的模型。

1.2.1物流Web服务组合模型

具体物流服务(concrete logistic service,CLS)是由物流服务提供商在服务注册中心中发布的可用物流服务。抽象物流服务 (abstract logistic service, ALS)是功能相似的一类物流服务集合。一个抽象物流服务包含多个具体物流服务，这些具体物流服务可由不同服务物流提供商提供，具有不同的QoS值。

根据对用户物流需求的分析，建立适当的物流服务流程模型。物流服务流程(logistic service processes,LSP)要完成多个功能，需要多个抽象物流服务的具体物流服务相互组合、配合。物流服务之间有顺序、选择、并行和循环等控制关系，如图3所示。

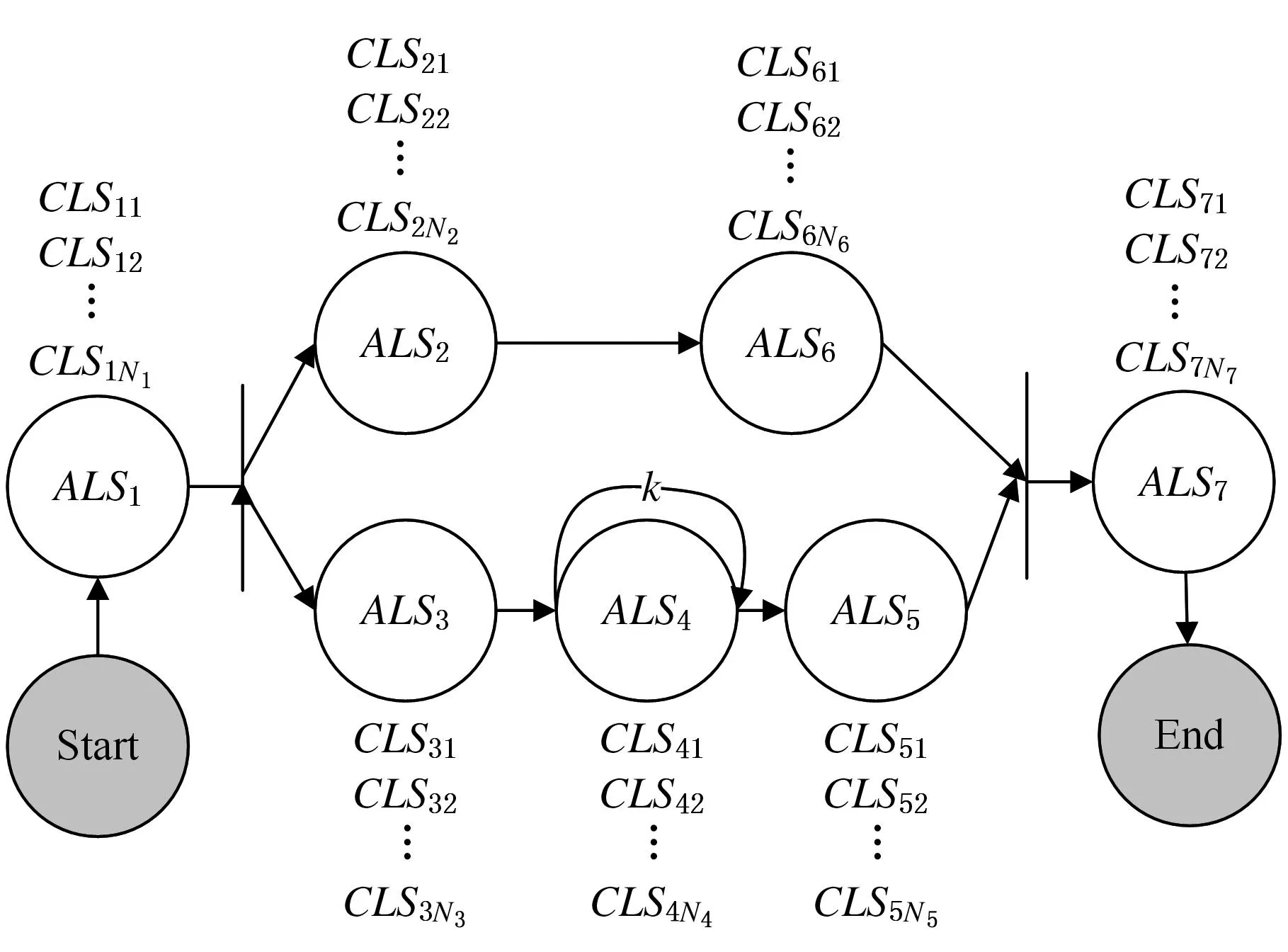
图3　物流服务流程示意图

假设一个物流服务流程由N个抽象物流服务组成，即LSP={ALS1，ALS2，…，ALSN}，每个抽象物流服务有Ni个候选具体物流服务，即ALSi={CLSi1, CLSi2…,CLSiNi}，每个具体物流服务有M个QoS属性：〈Q1,Q2,…,QM〉。物流服务组合就是为物流服务流程的每一个子流程服务选出一个具体物流服务，使物流服务整体评价达到最优，选出的具体物流服务集合称为组合物流服务，记作CS，物流服务组合流程示意图见图4。

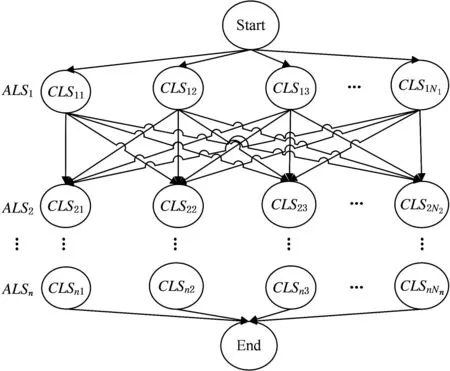
图4　物流服务组合流程图

1.2.2物流Web服务的QoS属性

目前已经提出且应用于实际的QoS属性指标有30多个，限于篇幅，本文只取物流服务中最常用、有代表性的5个QoS属性：费用(cost)C，即服务的成本，是获得服务所需支付的价格；时间(time)T，包括服务的运行时间、等待时间、通信时间等；信誉度 (credibility)Cr，即从服务使用者角度来评价一个服务的可信程度；递送的准时性(punctual)P，描述能够维护服务和服务质量的程度；可靠性(reliability)R，表示能够为Web服务请求提供服务的程度。

一个组合物流服务的QoS属性集表示为{C，T，Cr，P，R}。若抽象物流服务的连接为顺序结构，则描述组合物流服务的服务质量的聚合QoS的计算方式为

若抽象物流服务的连接为并行结构，则聚合QoS的计算方式为

若抽象物流服务的连接为混合结构，则聚合QoS的计算方式为上述两种计算方式的组合。

QoS属性的标准化采用如下极差标准化方法：

正向指标(最大化属性)标准化公式(以具体物流服务CLSia为例)为

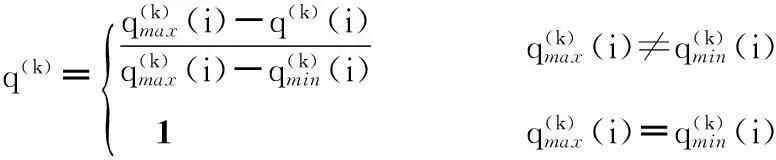
q(k)=q(k)max(i)-q(k)(i)q(k)max(i)-q(k)min(i) q(k)max(i)≠q(k)min(i) 1 q(k)max(i)=q(k)min(i){

(1)

负向指标(最小化属性)标准化公式为

q(k)=q(k)-q(k)min(i)q(k)max(i)-q(k)min(i) q(k)max(i)≠q(k)min(i) 1 q(k)max(i)=q(k)min{

(2)

2两阶段多目标蚁群算法

2.1基础蚁群算法概述

蚁群算法采用分布式并行计算机制，具有较强的鲁棒性，通过蚂蚁之间的协作机制来实现对多目标优化问题最优解的搜索。相比传统的穷举算法、贪婪算法，蚁群算法能够更快地找到问题的最优解，在许多组合优化问题上取得了较好的效果，如背包问题、TSP问题和车间调度问题、服务组合问题等。

蚂蚁的移动过程是蚁群算法解决物流服务组合问题的核心，利用蚁群算法求解物流服务组合问题模型中，当蚂蚁为当前抽象物流服务选出一个具体物流服务后，下一步则需要计算当前具体物流服务与下一个抽象物流服务所包含的所有具体物流服务的转移概率，采用轮盘赌方法确定蚂蚁的方向。转移概率计算公式为

(3)

i，j=1,2，…，N；a=1,2，…，Ni

式中，τ(i,a)(j,b)为具体物流服务CLSia到具体物流服务CLSjb路径上的信息素；η(j,b)为具体物流服务CLSjb的启发信息；α、β为信息素和启发函数的相对重要程度。

信息素的挥发与释放是蚁群算法正反馈机制的关键。基础蚁群算法采用如下规则进行信息素的更新：

τ(i,a)(j,b)(t+n)=(1-ρ)τ(i,a)(j,b)(t)+

Δτ(i,a)(j,b)0<ρ<1

(4)

(5)

i，j=1,2，…，N；a=1,2，…，Ni；b=1,2，…，Nj

式中，ρ为信息素的消逝速度；Q为预设常数；LCS为组合物流服务的服务质量构成的函数。

Dorigo提出了三种不同的信息素更新策略，本文采用应用最广泛的Ant-cyclesystem模型，模型中的LCS的计算公式如下：

(6)

启发函数的形式也有多种，本文基础蚁群算法的实现采用如下计算方法[8]：

(7)

2.2TMACO算法

目前，国内外很多学者已经从不同的角度将服务组合转换为以下的各种已知的数学问题，如单目标组合优化问题和多目标组合优化问题。单目标组合优化问题就是由用户给定各个QoS属性的权重值，通过简单的线性加权求和将多个QoS目标聚合转换为单目标，产生满足约束条件的优化结果为最优单解，用户没有选择的余地。

然而，服务的QoS属性之间存在不可公度性和矛盾性，难以将其值规范到统一的度量空间而准确地评估出服务的综合值，且用户缺乏QoS属性相关领域的知识，难以确切地给出QoS属性的权重信息，更难以用确切的数值来表达。因此基于QoS 的服务组合问题一般不存在通常意义上的最优解，讨论的多是非劣解。

所以本文选择将物流服务组合的组合优化问题转化为多目标组合优化问题来求解，即不需事先给定各QoS属性的权重值，对多个目标同时进行优化，最终产生一个非劣解集，用户可依其偏好从非劣解集中选择最满意的解，因此能更好地满足用户的偏好和个性化需求，也更符合物流服务组合的实际情景。

解决多目标问题的一般手段是通过对各个目标进行权衡和折中处理，得到不劣于其他解的一个解集，称为非劣解集(Pareto解集)[16]。Pareto支配及Pareto最优解集的定义如下。

Pareto支配当且仅当以下2个条件都成立时，称解x1支配解x2(目标为最小化)： ①fk(x1)≤fk(x2)(k=1,2,…,M)，即x1的各个目标都不比x2的各个目标差； ②∃k∈{1,2,…,M}:fk(x1)

Pareto最优解集在一个可行解的集合X中，那些不被X中任何一个解所支配的解的集合Xp(Xp⊂X)称为Pareto 最优解集。

为了有效求解物流Web服务组合问题，本文提出两阶段多目标蚁群算法TMACO算法。

2.2.1候选服务预优化阶段

本文讨论物流服务组合问题的基础是提供的具体物流服务都是可用服务，但是，在现有市场环境下，物流公司的整体实力良莠不一，他们所提供的具体物流服务的服务质量各方面也是参差不齐的。在候选具体物流服务集合中，不乏服务质量各方面都是较低水平的候选服务，即各个QoS属性值都较差，也就是被其他具体物流服务所支配。若算法的寻优能力足够优秀，那么这些被支配候选服务最终肯定不会出现在非劣解集中的组合服务中。因为若将组合服务中被支配候选服务替换成支配该候选服务的具体服务，则替换后的组合服务会支配替换前的组合服务。相关证明如下：

求证若组合服务中存在被支配具体物流服务，则该组合服务一定不是非劣组合服务。

已知CLSb支配CLSa，组合物流服务CSi包含CLSa。

证明记Q1为最大化属性(如可靠性)，Q2为最小化属性(如成本)，记CSi·Q1=ConΔCLSa·Q1，CSi·Q2=ConΔCLSa·Q2，Δ表示聚合，Con为常数；由于CLSb支配CLSa，因此有CLSb·Q1>CLSa·Q1，CLSb·Q2ConΔCLSa·Q1=CSi·Q1，ConΔCLSb·Q2

被支配候选服务的存在会大大延长算法的求解时间。基于此，本文提出候选服务预优化策略。算法后续的求解都是在候选服务预优化策略步骤后求得的非劣候选服务集中进行服务的选择。

定义一个具体物流服务被其他具体物流服务支配的程度(简称被支配因子)和支配其他具体物流服务的程度(简称支配因子)分别记为BD和D。

对于所有具体物流服务，必有0≤BD(CLS),D(CLS)

非劣具体物流服务集合按如下规则产生：对于任一个CLSia1，若不存在CLSia2，CLSia1与CLSia2属于同一个ALSi，且CLSia2支配CLSia1，则CLSia1属于非劣候选服务集。

2.2.2信息素的更新策略

基础蚁群算法求解服务组合问题时，采用个体中每两个相邻具体物流服务的相应QoS值的差值信息L来指导信息素的更新，L值越小，该个体释放的信息素越多。这种相对距离比较的方式没有考虑个体本身的优劣，因此寻优效果较差。对此，Wei等[9]提出了理想最优解的定义：一个理想解向量Fb是解空间中包含每个单目标最优值的点，Fb可能并不是候选集中存在的具体物流服务，它只是作为算法试图实现的一个目标。显然，越接近理想解的个体越优，理想解可由计算得到。

计算理想解与最差解的算法过程如下。

算法名称：CalFF(计算理想解与最差解的算法)

输入：全部组合物流服务的QoS值数据。

输出：解空间的理想解fb，最差解fw。

算法步骤：

(1)Fork=1 toM

(2)Fori=1 toN

(3)计算第i个抽象物流服务所包含的所有具体物流服务的k属性值的最大最小值maxki，minki;

(4)End For

(5)根据k属性的聚合计算方式,将N个minki相加或相乘，得到fb(k);将N个maxki相加或相乘，得到fw(k);

(6)End For

改进多目标蚁群算法信息素更新的条件为：在本轮迭代中，能够添加到Pareto解集的个体才能在相应路径上释放相应的信息素。

Pareto解集更新函数的具体实现步骤如下。

算法名称：ChangeParetoList

输入:解sca，Pareto解集PList。

输出:Pareto解集PList

算法步骤：

(1)IsGood=true;

(2)If PList.Lenght==0

(3)将sca插入PList;IsGood=true;

(4)End If

(5)For each sci in PList

(6)If sci支配sca

(7)IsGood=false;break;

(8)End If

(9)If sca支配sci

(10)将sci从PList中删除;continue;

(11)End If

(12)End For

(13)If IsGood==true

(14)将sca插入PList; IsInsert=false;

(15)End If

2.2.3启发函数的确定

基础蚁群算法中，启发函数的确定是由具体物流服务的QoS值确定的。在实际应用中，具体物流服务的QoS属性之间存在不可公度性，难以将其值规范到统一的度量空间，采用这种启发函数往往还是会出现侧重某一个或一些QoS属性的结果。而有些研究选择一个统一的常数作为启发函数，这样不能达到区分优劣的目的。本文在启发函数中考虑具体物流服务的支配因子，启发信息计算公式为

(8)

其中，N为抽象物流服务的个数。当候选服务集不大时，被支配候选服务较少，非劣候选服务集中候选服务的D值相差不大，此时的启发函数相当于一个常数。而当候选服务集较大时，采用这样的启发函数便能够较好地区分非劣候选服务的优劣，从而提高求解的速度。

2.2.4懒蚂蚁策略

日本北海道大学进化生物研究小组对蚁群的活动进行观察，发现大部分蚂蚁都努力地搜寻食物，而有少部分的蚂蚁却无所事事、左顾右盼，且称其为“懒蚂蚁”[17]。而在后续研究中发现，当断绝食物来源时，大部分的蚂蚁表现得一筹莫展，而“懒蚂蚁”们却能带领蚁群找到它们已侦察到的新食物源。“懒蚂蚁”不像其他大部分蚂蚁那样循规蹈矩，它们能观察到蚁群的薄弱之处，同时保持对新事物的探索状态，从而保证蚁群不断得到新食物源。这就是所谓的“懒蚂蚁效应”。

本文参考“懒蚂蚁效应”，在种群中划分出Ln个懒蚂蚁，它们并不像其他蚂蚁那样一步一步地求解，而是直接随机复制非劣解集中的一个个体的路径，并进行单位随机变异，作为自己的路径。采取这样的局部优化策略能够增加解的多样性，利于跳出局部最优的困局；同时，相对于随机生成解的方式，这样的策略能够较好地保持解的优良性，加快求解速度。

算法运行前期，加入解集中的解较少，新解加入的门槛较低，这时种群的寻解能力较强，而解集中解的平均质量不高，懒蚂蚁策略无法体现优势，因此懒蚂蚁应少些；随着解集的频繁更新，解的平均质量不断提高，新解加入的门槛提高，此时应设置多一些懒蚂蚁继承解集中的优解，并通过变异操作增加解的多样性，保持种群的寻优能力，促进算法跳出局部最优困局。因此，本文设置自动更新懒蚂蚁数量Ln的懒蚂蚁局部优化策略，即第一次迭代时，设置懒蚂蚁数为0；此后，根据每次迭代未能加入解集的蚂蚁数outAN,更新下一次迭代的懒蚂蚁数量，懒蚂蚁具体数量的计算方式如下：

Ln=θ·outAN

(9)

式中，θ为懒蚂蚁数量调整参数，0<θ<1。

2.3TMACO算法的实现步骤

(1)对原始候选服务集进行预优化。

(2)对算法进行初始化。初始化蚂蚁种群、各个参数以及非劣解集，计算每一个具体物流服务的D值、BD值，两阶段多目标蚁群算法迭代开始。

(3)为除懒蚂蚁外的其他蚂蚁计算当前具体物流服务到下一个抽象物流服务的所有具体物流服务的选择概率，用轮盘赌方法选择具体物流服务，将其序号加入蚂蚁的路径，聚合QoS值，直到蚂蚁得到一个完整的解。尝试更新非劣解集。

(4)懒蚂蚁局部优化策略。为每只懒蚂蚁复制解并进行单位变异，尝试更新非劣解集。

(5)信息素的更新。每段路径执行信息素的挥发操作。在本次迭代中，能成功更新非劣解集的解(包括懒蚂蚁)，在相应路径上释放信息素。

(6)调整懒蚂蚁的数量。

(7)若连续5次迭代，Pareto解集数量不变，则结束循环，输出非劣解集；否则，返回步骤(3)，继续迭代。

2.4TMACO算法的时间复杂度分析

TMACO算法求解物流服务组合问题模型中，蚂蚁种群规模为AN，最大迭代次数为MAXNC，算法的时间复杂度分析如下：

初始化算法各参数，计算具体物流服务的D值及BD值(需要常数次)，时间复杂度为O(N×Ni2)；初始化蚂蚁种群需要AN次，时间复杂度为O(AN)；寻优过程，AN只蚂蚁构造一次解，与非劣解集中的所有解进行比较，算法总共迭代MAXNC次，时间复杂度为O(MAXNC×(AN2+AN3))。

3实验结果与分析

为了验证本文算法的可行性及实用性，本文所有算法均运用Java编程语言，运用MyEclipse软件编写实验相关代码。本实验编译运行的计算机参数为：32位Windows 7操作系统、Intel Core 2 E8400 3.00GHz CPU、2.00GB内存。

本文实验中，参照文献[10]，每个候选物流服务抽取五个QoS指标，即交付时间T、交付费用C、交付可靠性R、递送的准时性P及信誉度Cr。QoS属性的取值范围设置如下：1 h≤T≤24 h，1≤C≤100，0.5≤R≤1，0.5≤P≤1，0.5≤Cr≤1。

根据文献[18]得出的蚁群算法相关参数范围，本文选择的参数值分别为：α=1，β=5，ρ=0.7，Q=10。各维QoS的权重分别为0.15，0.2，0.25，0.1，0.3[10]。

3.1TMACO算法参数分析

为探究蚂蚁种群数量以及懒蚂蚁数量调整参数的设置对算法寻优效果的影响，实验设置25个参数组合，分别是蚂蚁种群AN的5个取值和懒蚂蚁数量调整参数θ的5个取值的两两组合，其中参数组合1～5为AN取值70，θ取值依次为0.3、0.4、0.5、0.6、0.7，组合6～10、11～15、16～20、20～25的AN取值分别为90、110、130、150，θ取值与1～5组合一致。

实验选取抽象物流服务个数N为6，每个抽象物流服务所包含的具体物流服务个数为区间[5,10]内随机选择。实验分别独立运行10次，从以下六个方面考查算法的性能：①平均解个数(非劣解的平均数量，即0次非劣解数量的平均值)；②最多解个数(非劣解最多数量，即10次非劣解数量的最大值)；③平均收敛时间(找到所有非劣解的时间的平均值，即10次收敛时间的平均值)，收敛时间的单位为s；④最短收敛时间(找到所有非劣解的时间的最短时间，即10次收敛时间的最小值)；⑤平均解值(每次运行得到一个最优解，即10次最优解的平均值)；⑥最优解(10次最优解的最小值)。

实验结果如图5～图8所示。

由图5的组合1～5可见，随着懒蚂蚁数量调整参数θ的增大，TMACO算法找到的平均非劣解个数、最多解个数增多，到组合4，即当θ值为0.6时，增加趋势变缓，其他组合(如组合6～10、11～15等)的情况类似；从整体上看，到组合16～20，即蚂蚁种群个数AN达到130时，非劣解的增加趋势变得缓慢。因为解空间的非劣解数量是固定的，所以随着蚂蚁数量AN的增加，蚂蚁对解空间的搜索能力增强，能够找到的非劣解数量也随之增加；但当AN增加到一定数量时，能找到的解空间中的非劣解越来越少，直到所有非劣解被找到。

图5　两个参数对找到非劣解的个数的影响

由图6可见，所有参数组合找到的最优解都是一致的，即所有参数组合在独立运行10次的情况下，至少有一次能找到指定权重的问题的最优解，证明了TMACO算法求解该问题的有效性。从整体上看，随着AN和θ的增大，平均解值有减小的趋势，波动范围在0.02以内，其中，组合25得到的平均解值逼近最优解值，说明10次独立运行所得到的最优解的质量都较高。

图6　两个参数对算法找到非劣解的解值的影响

由图7可见，随着AN和θ的增大，平均收敛代数越来越少，收敛时间越来越长，即蚂蚁数量越多，懒蚂蚁数量比例越大，算法找到越多非劣解所需循环次数越少。而最小迭代代数的变化规律不太明显。由图8可见，收敛时间随着蚂蚁数量和懒蚂蚁比例的增加而增加，蚂蚁数量达到130时，增加趋势变缓；同样蚂蚁数量的5组实验中，θ值取0.6时，收敛时间增加幅度较小。

综上，本文算法参数设置为：AN=130，θ=0.6。

图7　两个参数对算法收敛代数的影响

图8　两个参数对算法收敛时间的影响

3.2不同规模下TMACO算法的效果分析

为探究TMACO算法对求解Web服务选择问题的稳定性及有效性，对问题设置不同实验规模，本文设置7组不同规模的实验，每组的抽象物流服务个数分别为6,9,12,15,18,21,24，每组中，每个抽象物流服务所包含的具体物流服务个数从区间[5,10]内随机选择。实验从算法寻得的非劣解数量、最优解适应度值、收敛代数、收敛时间四个方面考查算法的性能。

图9、图10所示为TMACO算法求解不同规模的Web服务选择问题的实验结果。

由图9可见，随着问题规模的增大，TMACO算法寻得问题的非劣解数量、非劣解的适应度值均线性增大，且问题规模越大时，非劣解适应度的增大趋势渐缓，因为问题规模的增大，解空间中解的数量增多，非劣解数量也随之增多，适应度值的基数增大，适应度值也增大。TMACO算法在求解Web服务选择问题上表现出了有效性及较好的稳定性。由图10可见，TMACO算法在求解Web服务选择问题时的收敛代数和收敛时间随着问题规模的增大而增大，收敛时间的延长趋势明显，因为，随着问题规模增大，解空间非劣解数量增多，Pareto解集中的解较多，导致算法每求得一个解，需要与之进行比较的次数激增，因此收敛时间延长趋势明显。

图9　不同规模下TMACO算法寻得的解的情况

图10　不同规模下TMACO算法的收敛情况

3.3TMACO算法各策略效果对比

为验证本文TMACO算法的各策略对算法效果的贡献，设置对比实验，在TMACO算法基础上，分别加以下限制条件：去掉预优化策略(A)、采用基础蚁群算法的信息素更新(B)、采用基础蚁群算法的启发信息(C)、去掉懒蚂蚁局部优化策略(D)。实验选取抽象物流服务个数N为21，每个抽象物流服务所包含的具体物流服务个数从区间[5,10]内随机选择。考查指标与3.2节相同。实验结果如图11、图12所示。

图11　本文算法各策略寻得的解的情况

图12　本文算法各策略的收敛情况

由图11可见，在寻得非劣解数量上，TMACO算法最多，D算法最少；在最优解适应度上，TMACO算法最优，D算法最差，即没有懒蚂蚁策略的算法(D)效果最差，说明懒蚂蚁策略在增加算法多样性上效果较好，其对TMACO算法寻优性能方面的贡献较大，信息素更新策略(B)次之。由图12可见，在收敛代数上，TMACO算法最少，说明TMACO算法用较少的迭代次数就能找到更多的非劣解，其次是A算法，D算法最多，即去除懒蚂蚁策略时，算法需要较多次迭代才能找到更多非劣解，说明懒蚂蚁策略在提高算法收敛速度上贡献较大；在收敛时间上，D算法最短，TMACO算法最长，说明懒蚂蚁策略较其他两种策略在TMACO算法时间上占据较大比重，预优化策略次之。

综上，在算法的寻优性能和收敛速度上，懒蚂蚁策略和信息素更新策略贡献较大，这两种策略是TMACO算法的核心。

3.4TMACO算法与其他算法的对比

为了验证本文算法的寻优效果，设置对比实验，分别为：文献[19]中的基础遗传算法、文献[5]中的改进遗传算法、文献[8]中的基础蚁群算法、文献[9]中的改进蚁群算法。遗传算法的参数均参照各自文献来源进行设置。实验选取的问题规模、考查指标均与3.3节相同。实验结果如图13、图14所示。

图13　TMACO算法与其他算法寻得的解的情况

图14　TMACO算法与其他算法的收敛情况

由图13看出，从寻得非劣解数量上看，TMACO算法最多，改进遗传算法次之，基础蚁群算法最少；从解的适应度值上看，TMACO算法的最优解的适应度值最优，其次是改进遗传算法，说明TMACO算法的寻优性能较好，不仅能较其他算法找到更多的非劣解，更能找到适应度值较优的非劣解。由图14可看出，在收敛时间上，蚁群算法普遍长于遗传算法，因为遗传算法的时间复杂度要小于蚁群算法的时间复杂度。TMACO算法的收敛时间只比文献[9]的改进蚁群算法稍长。而从收敛代数上看，TMACO算法最少，其次为改进遗传算法，即TMACO算法收敛只需较少的迭代次数。由此可见，较之其他算法，TMACO算法能以较少迭代次数找到较多、且质量优的非劣解。

综上所述，本文提出的TMACO算法在求解基于QoS的物流Web服务组合问题上，表现出了良好的寻优性能和收敛特性，是一种有效的组合优化问题求解方法。

4结语

本文重点研究了基于QoS的物流Web服务选择问题。为了实现物流资源的有效整合，阐述了一种物流资源表达和服务封装的方法。此外，为了为每一个物流阶段找到最优的具体物流服务，建立了基于QoS的物流Web服务选择模型，并通过提出的两阶段多目标蚁群算法来求解该问题。但是本文对服务组合过程中物流Web服务的动态性、不稳定性等问题并未进行讨论，还需要进一步的研究。下一步我们将在更多数据集中验证TMACO算法的性能，对算法参数的优化选择以及算法的收敛问题进行研究，并进一步寻找制约蚁群算法收敛速度的深层原因以及算法对数据敏感性的规律。

参考文献：

[1]GuinardD,TrifaV,KarnouskosS,etal.InteractingwiththeSOA-basedInternetofThingsDiscovery,Query,Selection,andOn-demandProvisioningofWebServices[J].TransactionsonServicesComputing， 2010,3(3):223-235.

[2]SchuldtA,HribernikKA,GehrkeJD,etal.CloudComputingforAutonomousControlinLogistics[C]∥Proceedingsof40thAnnualConferenceoftheGermanSocietyforComputerScience.Berlin, 2010:305-310.

[3]HoltkampB,SteinbussS,GsellH,etal.TowardsaLogisticsCloud[C]∥ProceedingsoftheSixthInternationalConferenceonSemantics.Beijing,2010:305-308.

[4]GarruzzoS,RosaciD,SarnèGML.IntegratingTrustMeasuresinMulti-agentSystems[J].InternationalJournalofIntelligentSystems， 2012,27:1-15.

[5]刘磊,杨冬.求解服务等级感知服务组合问题的多目标遗传算法[J].吉林大学学报,2015，45(1)：267-273.

LiuLei,YangDong.Multi-objectiveGeneticOptimizationAlgorithmforSLA-awareServiceCompositionProblem[J].JournalofJilinUniversity,2015，45(1)：267-273.

[6]刘志中,宋成,薛霄,等.情景感知的物流Web服务动态优化组合研究[J].计算机工程与科学,2013,35(9):51-56.

LiuZhizhong,SongCheng,XueXiao,etal.ResearchonDynamicOptimalCompositionofContext-awareLogisticsWebService[J].ComputerEngineering&Science, 2013,35(9):51-56.

[7]盛国军,温涛,郭权,等.基于改进粒子群的Web服务组合[J].计算机学报,2013, 36(5):1031-1045.

ShengGuojun,WenTao,GuoQuan,etal.WebServiceCompositionBasedonModifiedParticleSwarmOptimization[J].ChineseJournalofComputer,2013, 36(5): 1031-1045.

[8]王秀亭,马力.基于蚁群算法的Web服务选择[J].现代电子技术, 2013,36(12):9-11.

WangXiuting,MaLi.WebServiceSelectionBaseonAntColonyAlgorithm[J].ModernElectronicsTechnique, 2013,36(12):9-11.

[9]WeiZ,CarlK,TaimingF,etal.QoS-basedDynamicWebServiceCompositionwithAntColonyOptimization[C]//ACSAC2010:IEEE34thAnnualComputerSoftwareandApplicationsConference.Vasteras,Sweden,2010:493-502.

[10]张焕焕,薛霄,刘志中,等.基于遗传社会认知算法的物流Web服务优化组合研究[J].计算机应用研究,2014,31(6):1752-1754.

ZhangHuanhuan,XueXiao,LiuZhizhong,etal.ResearchonOptimizationofLogisticsWebServiceBasedonGenrticSocialCongnitiveOptimizationAlgorithm[J].ApplicationResearchofComputers, 2014,31(6):1752-1754.

[11]ZhaoS,MaL,WangL,etal.AnimprovedAntColonyOptimizationAlgorithmforQoS-awareSynamicWebServiceComposition[C]//ICICEE2012:InternationalConferenceonIndustrialControlandElectronicsEngineering.Xi’an, 2012:1998-2001.

[12]SahooJ,MohapatraS,LathR.Virtualization:aSurveyonConcepts,TaxonomyandAssociatedSecurityIssues[C]∥ICCNT2010:Proceedingsof2ndInternationalConferenceonComputerandNetworkTechnology.Bangkok,Thailand, 2010:222- 226.

[13]LiWenfeng,ZhongYe,WangXun,etal.ResourceVirtualizationandServiceSelectioninCloudLogistics[J].JournalofNetworkandComputerApplications, 2013,36(6): 1696-1704.

[14]AtzoriL,IeraA,MorabitoG.TheInternetofThings:aSurvey[J].ComputerNetworks,2010,54: 2787-2805.

[15]CanforaG,PentaMD,EspesitoR,etal.ALightweightApproachforQoS-awareServiceComposition[C]∥PICSOC2004:Proceedingsofthe2ndInternationalConferenceonServiceOrientedComputing.NewYork:ACM, 2004:36-47.

[16]郑彦兴,田菁,窦文华.基于Pareto最优的QoS路由算法[J],软件学报,2005, 16(8): 1484-1489.

ZhengYanxing,TianJing,DouWenhua.AQoSRoutingAlgorithmBasedonParetooptimal[J].JournalofSoftware,2005,16(8): 1484-1489.

[17]罗仕奎.懒蚂蚁效应——懒于杂务,才能勤于动脑[J].北京农业,2011,36(8):13-14.

LuoShikui.LazyAntEffect—LazyChorestoBeDiligentinTheirBrains[J].BeijingAgriculture, 2011,36(8):13-14.

[18]杨亚南.蚁群算法参数优化及其应用[D].南京:南京理工大学,2008.

[19]方周,陈荣平,蔡美玲.遗传算法在Web服务组合中的应用[J].计算机与现代化,2007, 48(12): 118-121.

FangZhou,ChenRongping,CaiMeiling.ApplicationofGeneticAlgorithmsinWebServiceComposition[J].ComputerandModernization, 2007,48(12):118-121.

(编辑苏卫国)

Two-stage Multi-objective Ant Colony Optimization for Solving Logistics Web Service Composition

Fang QinghuaNi LipingLi Yiming

Hefei University of Technology,Hefei,230009

Abstract：A two-stage multi-objective ACO(TMACO) was proposed to solve logistics Web services composition optimization problems. First, to solve the time increases rised by candidate services which was dominated in the raw data, a pre-optimization strategy was proposed based on Pareto dominated ideology; secondly, since the weights of each attribute were difficult to determine, a non-dependent weight pheromone update strategy and inspiration information policy were included in the TMACO; and finally, the basic ACO was easy to fall into local optimum problem, a lazy ant strategy was proposed to solve this problem. The experimental results show that TMACO algorithm has good performance. Its optimization capability is better than that of the basic ACO,the improved ACO which used the distance of the solution and the ideal solution to update the pheromone,the basic genetic algorithm and improved genetic algorithm which applied the dominant factor to evaluate a solution, TMACO optimization algorithm has a higher ability to find more and better Pareto solutions.

Key words:logistics service; ant colony optimization (ACO); service composition problem; Pareto optimal solution; multi-objective optimization

收稿日期：2015-06-12

基金项目：国家自然科学基金资助项目(71301041,71271071)

中图分类号：TP181

DOI：10.3969/j.issn.1004-132X.2016.10.009

作者简介：方清华，女，1990年生。合肥工业大学管理学院硕士研究生。研究方向为数据挖掘、群体智能优化算法。倪丽萍，女，1981年生。合肥工业大学管理学院副教授。李一鸣，男，1990年生。合肥工业大学管理学院硕士研究生。