单级放大机电集成压电谐波电机设计与仿真分析

高立超　许立忠　李　冲

燕山大学，秦皇岛，066004



单级放大机电集成压电谐波电机设计与仿真分析

高立超许立忠李冲

燕山大学，秦皇岛，066004

摘要：设计了一种单级放大机电集成压电谐波电机，阐述了该种电机的工作原理，给出了其设计方法、连续传动条件及参数选择原则。针对电机中容易发生失效的区域，推导了最大应力公式，通过有限元仿真对比验证了理论公式的正确性。分析了电机的固有频率和振型以及电机在简谐激励下的位移和应力响应。结果表明：电机理论最大应力为45.54 MPa，与仿真最大应力相差4.04%；激励作用下，活齿振动位移最大，活齿架应力集中最严重。

关键词：单级放大；压电谐波电机；最大应力；有限元仿真

0引言

压电电机是一种利用压电材料的逆压电效应使压电体变形产生往复振动，通过传动机构将振动位移转换为直线或旋转运动的新型复合电机[1]。与电磁电机相比，压电电机具有结构简单、响应速度快、定位精度高等优点[2]。Toyama[3]设计了一种球形压电超声电机，并将该种电机作为相机作动器安装在管状探测机器人上；Tomoaki[4]研制了一台定子体积只有1 mm3的微型压电超声电机，该电机成为最小的压电电机之一；朱鹏举等[5]设计了一种大推力直线压电电机，当驱动频率为100 Hz时，该电机最大输出力为130 N；张海峰等[6]设计了一种高效压电旋转驱动器，解决了压电双晶片旋转驱动器能量利用效率低的问题；Chen等[7]利用20个压电堆和20个块状弹簧产生的行波，研制了一台利用径向弯曲模态的行波压电超声电机。

传统压电电机主要靠摩擦传动，其缺点是接触面磨损严重、寿命短，非接触式压电电机虽避免了定转子间的摩擦，但其承载能力较低，而压电谐波电机却能克服上述缺陷。2000年，德国学者Barth[8]提出利用谐波齿轮箱和压电堆传动的谐波压电电机，利用齿轮箱的柔轮代替了传统的行波发生器。2004年，辛洪兵等[9]设计了一台利用位移放大机构的压电谐波电机。以上谐波电机采用了谐波齿轮传动，造成柔轮承受较大的交变载荷，且谐波齿轮传动比下限值较高[10]。

基于上述原因，许立忠等[11-12]提出了一种既降低摩擦损耗、延长电机寿命，同时又增大电机输出力矩的机电集成压电谐波电机，该种电机利用活齿啮合取代定转子间的摩擦力来驱动转子，具有低速、大转矩等特性。为了增大电机的输出转矩，本文对机电集成压电谐波电机进行了改进，设计出单级放大机电集成压电谐波电机。经过理论计算，机电集成压电谐波电机的输出力矩为0.11 N·m，而单级放大机电集成压电谐波电机的输出转矩为3 N·m，故单级放大电机更具优势。本文给出了单级放大机电集成压电谐波电机的设计过程，并进行了电机关键零部件的有限元仿真。

1电机工作原理

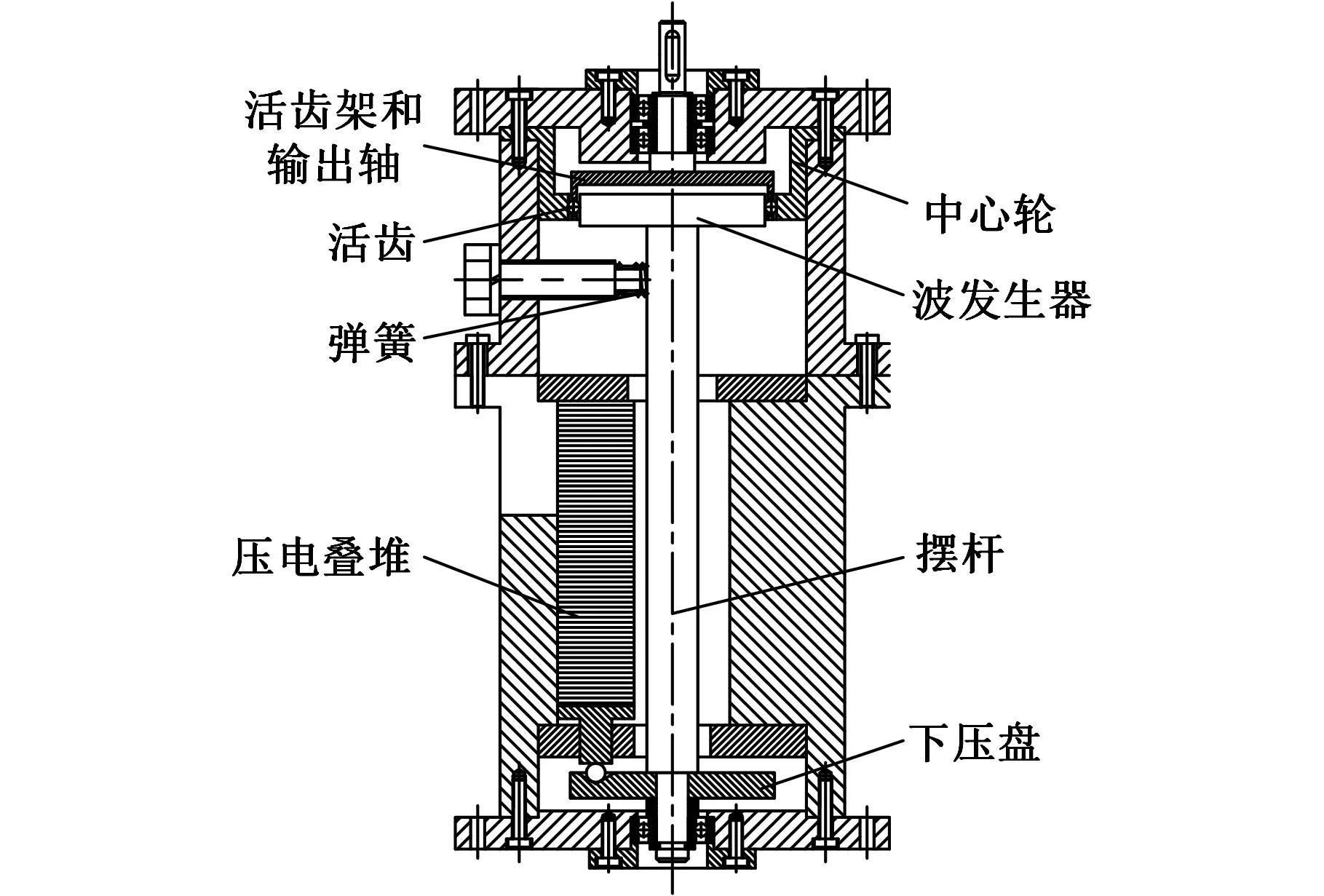
图1　单级放大机电集成压电谐波电机

单级放大机电集成压电谐波电机如图1所示，该电机由驱动部分和传动部分组成，驱动部分主要包括压电叠堆(2个)、下压盘、摆杆和弹簧(2个)，传动部分主要包括波发生器、中心轮、活齿(30个)、活齿架和输出轴。电机中，下压盘和摆杆共同构成单级放大机构，下压盘相当于杠杆，支点位于底座轴承的中心处。电机中2个压电叠堆以相位差90°分布于摆杆外侧(图1中只显示出一个压电叠堆，另一个在摆杆后面未显示出来)。工作时，分别给2个压电叠堆通入相位差90°、带正偏置的余弦信号，压电叠堆在激励信号作用下发生伸缩变形，压电叠堆带动下压板发生左右和前后摆动，同时由于摆杆和下压板固连，故摆杆能够同时发生左右和前后摆动，在连续信号作用下，波发生器边缘处就形成了连续谐波。这种通过摆杆摆动形成谐波与传统圆周转动形成谐波在形式上不同，但谐波效果相同。谐波力推着活齿沿齿廓方向滑动，活齿架在活齿带动下转动一定角度。以此类推，在输出轴端获得连续转动。

电机设计指标如下：传动比为30，单级放大倍数大于6，偏心距0.1 mm，输出转矩3 N·m，转速小于等于6 r/min。

2电机参数设计

电机传动部分活齿系统如图2所示。本文设计活齿个数Zp=30，中心轮波齿数Zc=29，则电机活齿系统传动比为

(1)

设计电机活齿系统偏心距a=0.1mm。中心轮齿廓是活齿传动的关键部位，中心轮齿廓方程为

X=bcos[θ-arcsin(asin(icp-1)θ/b)]+

acosicpθ±rpcosψ

Y=bsin[θ-arcsin(asin(icp-1)θ/b)]+

asinicpθ±rpsinψ

b=rs+rp

式中，θ为活齿架转角；ψ为活齿中心运动轨迹上该点法线与x轴的夹角；rs、rp分别为波发生器和活齿的半径；X、Y为中心轮齿廓坐标。

图2　活齿传动系统图

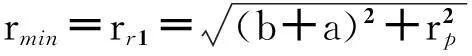
(1)

(2)

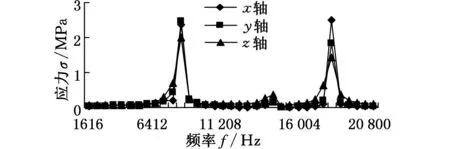
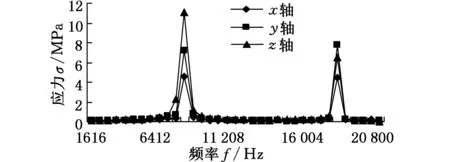
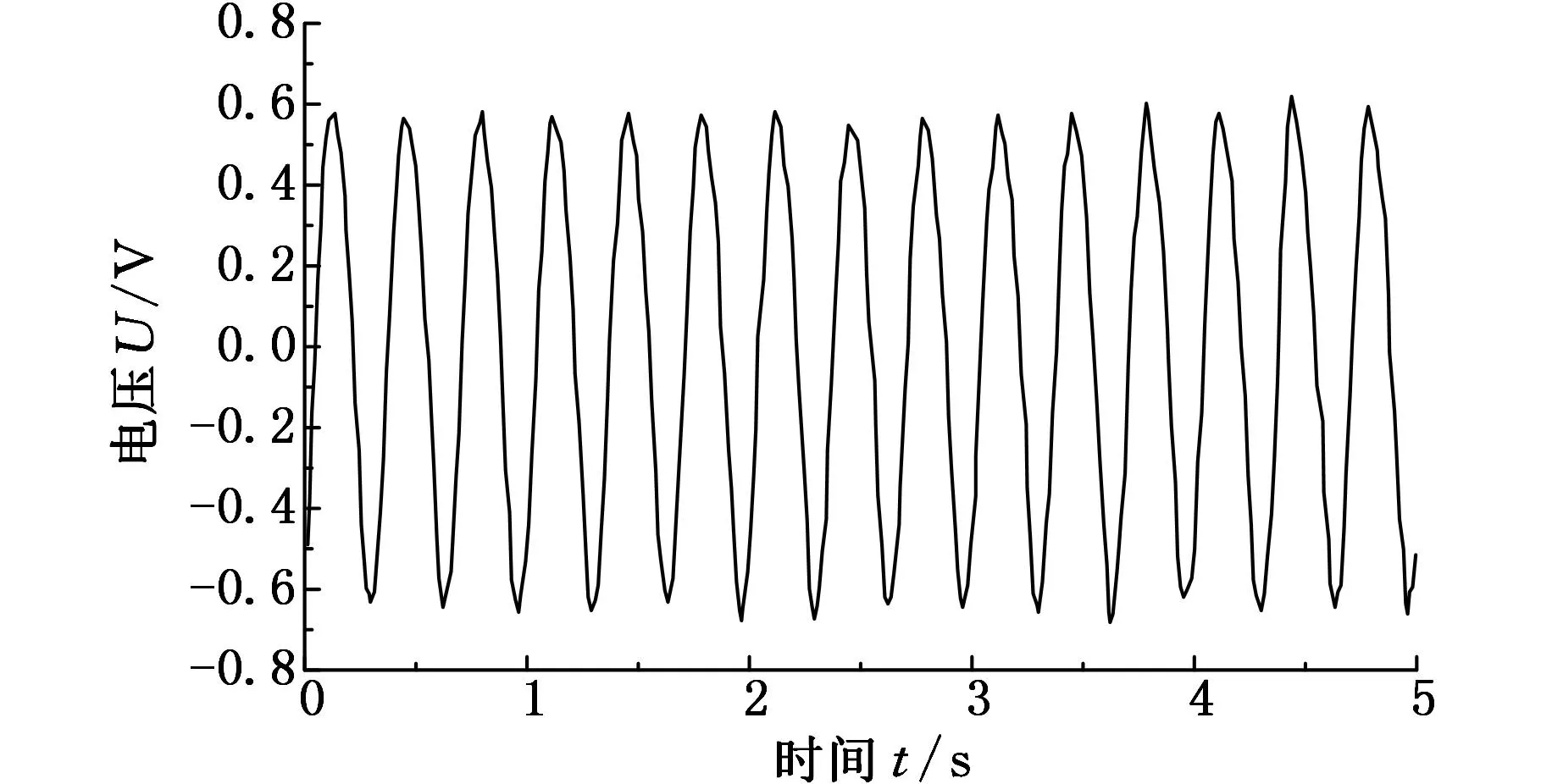
(a)齿根位置　　　　　(b)齿顶位置图3　活齿在中心轮齿廓上的几何关系

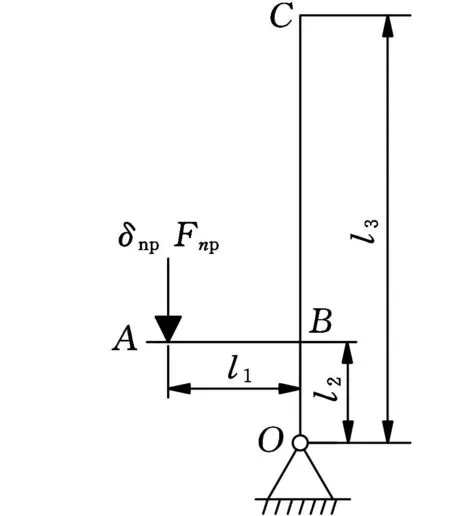
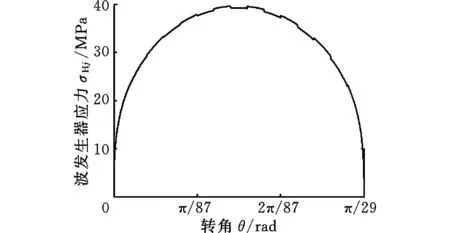
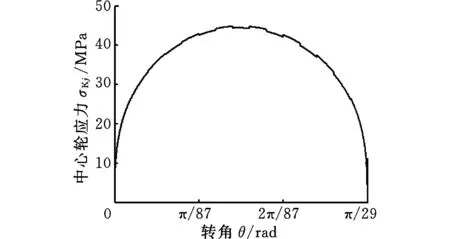
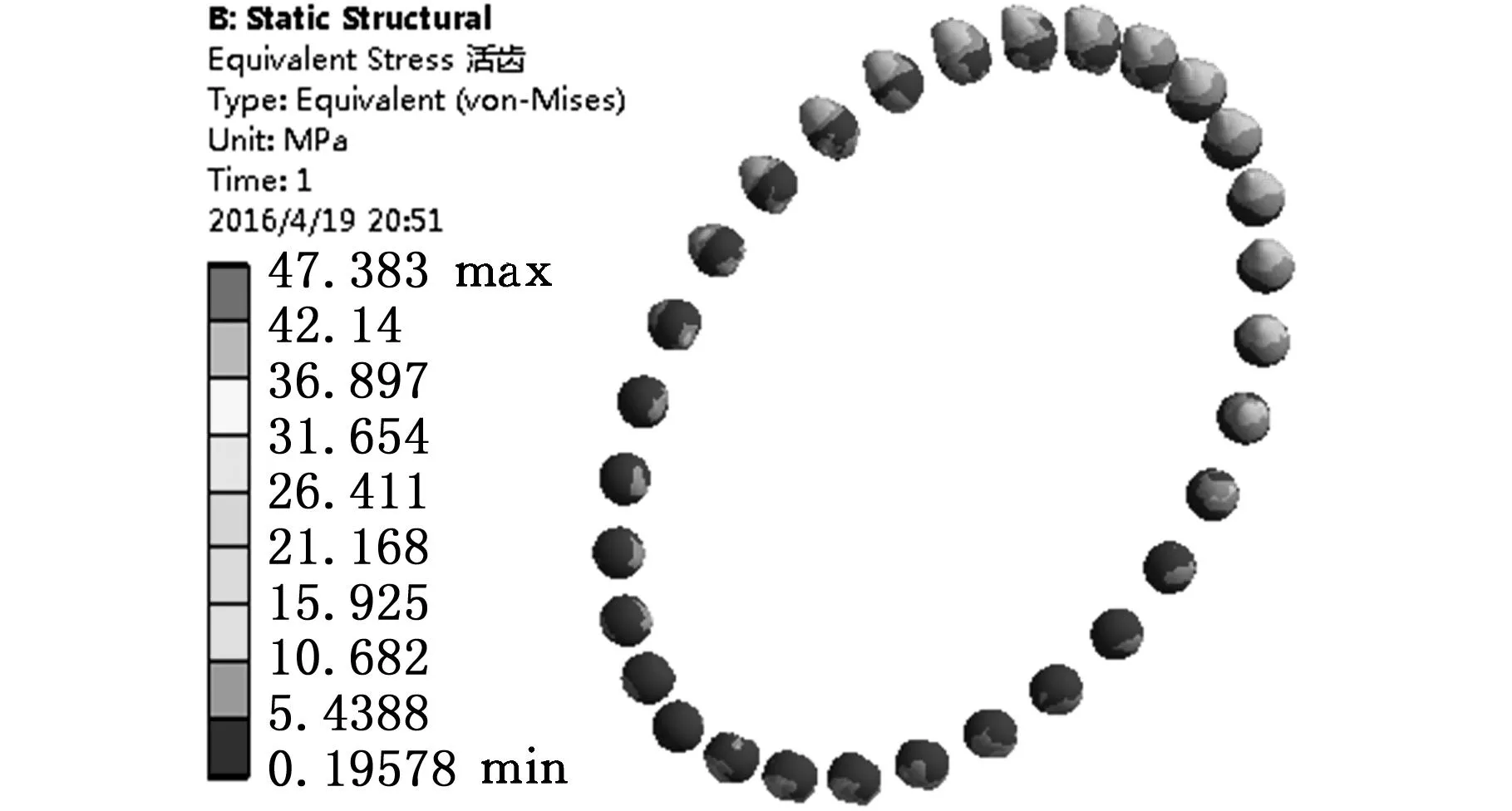
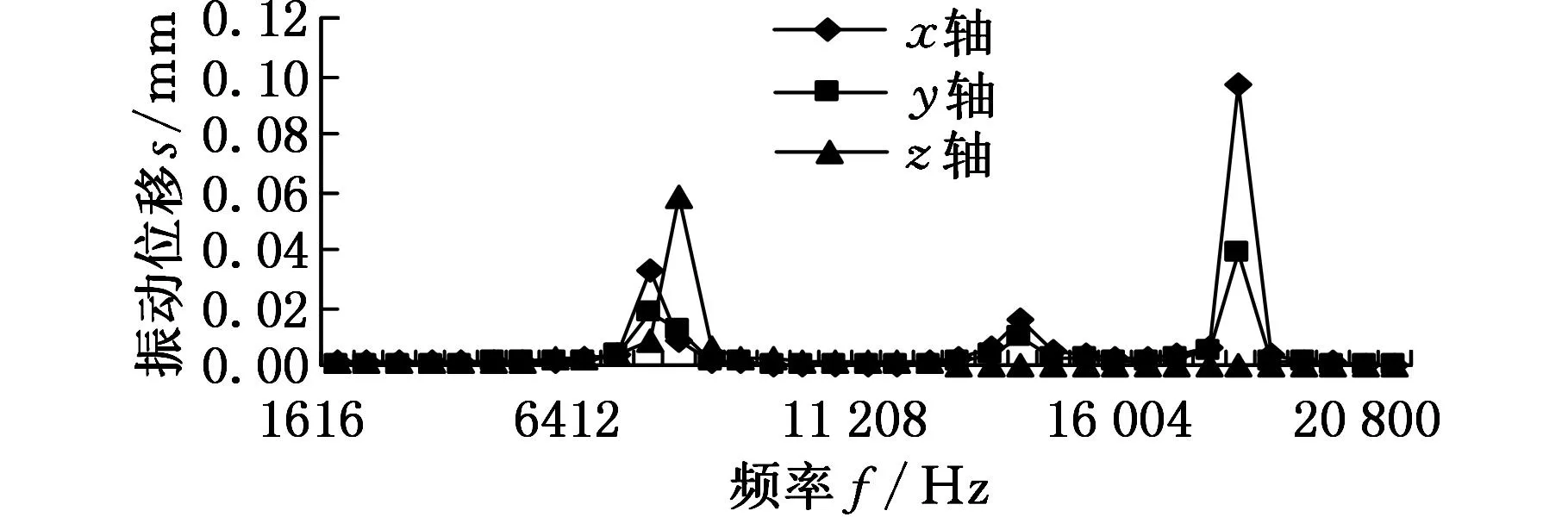
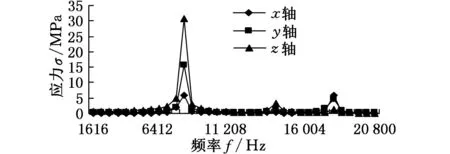
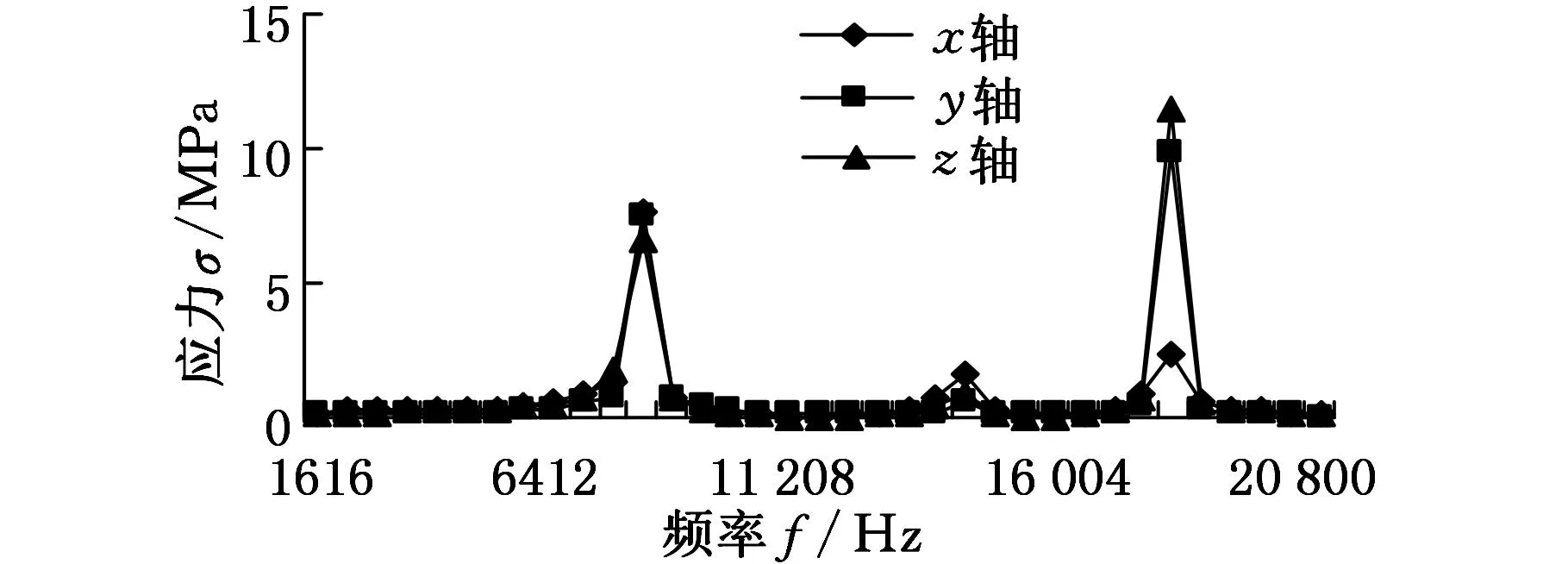
取波发生器半径rs=14.5mm，活齿半径rp=1mm，由式(1)和式(2)可得15.6mm

本文选用结构尺寸为10mm×10mm×50mm的压电叠堆作驱动源。图4为驱动部分计算图，其中δnp、Fnp分别为压电叠堆最大变形量和最大输出力，l1为压电叠堆作用力臂，l2为下底板与摆杆铰支点间的距离，l3为波发生器边缘与摆杆铰支点间的距离。由位移关系可得

δnp/l1=δB/l2

δB/δC=l2/l3

式中，δB、δC分别为图4中B、C点的位移。

则波发生器边缘处的位移为

δC=δBl3/l1

对O点取矩，可得C点垂直于摆杆的力为

FC=Fnpl1/l3

图4　驱动部分计算图

已知压电叠堆最大位移δnp=0.05mm，最大输出力Fnp=3600N，l1=13mm，l3=95mm，则波发生器边缘处C点的位移为δC=0.365mm，受力为FC=492.6N。故单级放大机构的放大倍数为δC/δnp=7.3。当偏心距a=0.1mm时，波发生器位移大于等于0.2mm时才能够使活齿系统发生连续转动，δC>0.2mm满足连续转动条件。

3电机静力学分析

3.1电机传动力学模型

活齿受力如图5所示，活齿分别受波发生器作用的力FHj、活齿架作用的力FSj和中心轮作用的力FKj。假设活齿架的转角为θ，则βj=[θ0+icpθ+2π(j-1)/icp]/icp，θ0为初始位置活齿架角度。波发生器的转角β1j=icpβj，由βj和β1j可得β2j=(icp-1)βj，β3j=arcsin(asinβ2j/b)，j表示第j个活齿。前文中已得出波发生器受力FC，该力等于各参与啮合活齿受力FHj的合力,即

(3)

θHj=θ0+iθ+β3j+2π(j-1)/i

分别在x、y方向上对活齿列平衡方程，得

(4)

式中，αj为活齿中心运动轨迹切线与x轴夹角，αj=-dy/dx。

活齿的中心运动轨迹方程为

(5)

联立式(3)～式(5)即可求得活齿受力FHj、FSj和FKj。

当两弹性体接触时，假设两弹性体沿接触点切平面法线方向受到的分布压力的合力为F(FHj、FSj或FKj)，接触点处应力为σ，如图6所示，则两弹性体曲面方程和接触点附近应力分别为

(6)

(7)

式中，S为两弹性体接触面在切平面上投影的面积，mm2。

图6　应力计算模型

两弹性体接触点附近表面上与切平面垂线相交的两点之间的直线距离为z1+z2，则

z1+z2=Ax2+By2

(8)

式中，k11、k12、k21、k22分别为两弹性体在接触点处的主曲率；η1和η2分别为在切平面内进行坐标变换时坐标轴间的夹角。

由式(4)知，接触面在切平面上的投影为椭圆，F在椭圆内部某点引起的垂直位移W为

(9)

D(e)=(K(e)-E(e))/e2

式中， E、μ分别为材料的弹性模量和泊松比；a1、b1分别为两弹性体接触面投影的长半轴和短半轴；e为椭圆率；K(e)、E(e)为系数。

根据弹性体理论，假设接触点附近两点变形后位移为W1+W2，δ为接触变形量，则接触面内在平行于接触点切平面法线方向上任意两点的位移方程为

z1+z2=δ-(W1+W2)

(10)

由式(8)～式(10)可得

(11)

联立式(7)、式(11)，可得应力方程为

(12)

将式(12)中的F替换为FHj、FSj和FKj即可得到活齿受到的应力。

3.2应力求解与分析

活齿系统是单级放大机电集成压电谐波电机中传递运动最为核心的部分，由于活齿在工作过程中与构件间是点接触，故活齿是整个电机较为薄弱的受力点，因此对活齿进行应力分析是非常有必要的。图7是由式(12)通过理论计算得到的活齿应力随活齿架转角的变化曲线，图8是对电机进行有限元仿真得到的活齿应力云图。

(a)σHj随转角θ变化

(b)σKj随转角θ变化

(c)σSj随转角θ变化图7　活齿所受各应力随活齿架转角变化曲线

由图7、图8可知：

(1)活齿架每转过π/29时，活齿所受各应力又回到最小值；在活齿架每转过奇数个π/58时，活齿所受各应力达到最大值。

(a)网格划分

(b)活齿应力云图图8　活齿有限元分析

(2)活齿所受应力随活齿架转角变化而出现突变现象，且每经过π/435时应力突变一次。这是由于当系统有30个活齿工作时，只有一半左右的活齿处于啮合状态，且啮合活齿数始终在15齿和16齿之间跳跃变化，同时啮合齿数变化周期为π/435，故活齿应力会在π/435时发生突变。

(3)在活齿应力云图中，只有一半左右的活齿所受应力较大，且处于中间的几个啮合活齿的应力值达到最大值，这与图7中应力曲线的规律是一致的。

(4)理论计算活齿最大应力处于活齿与活齿架啮合处，为45.54MPa，有限元得到的最大应力为47.38MPa，误差为4.04%。

4电机动力学分析

4.1模态分析

单级放大机电集成压电谐波电机结构较复杂，其形状变化多样且材料特性各异，目前很难用解析法获得精确的动力学解，且模型简化求解得到的误差较大，无法满足电机性能要求。而有限单元法可以较准确地模拟电机的动态特性。

用单元节点位移场表示单元应变场如下：

Bm=LmNm

假设压电片上下面各存在一个电势自由度qu和qd，等势面上的节点共用此一对电势自由度，即

qe=[quqd]T

假设压电堆内电场均匀分布，电场强度表示为

E=[ExEyEz]T=Beqe

式中，Be为系数矩阵；lp为压电片厚度。

则单元体动能表示为

弹性单元体势能为

压电单元体势能为

式中，D为电位移;σ为压电堆应力；Ve为单元体体积。

由Hamilton原理可得，电机机电耦合方程为

(13)

式中，Mmm、Kmm、Kme、Kee分别为质量矩阵、刚度矩阵、压电耦合矩阵和介电传导矩阵；Qq为压电片电荷量；Ff为广义力列向量。

电机自由振动方程可简化为

式中，ω0为系统的固有频率。

应用上述有限元法对单级放大机电集成压电谐波电机进行模态求解，得到电机部分固有频率及振型，如表1所示。由表1可知：

(1)当频率较低时对应的振型多数是驱动部分的振动，频率较高时对应的振型多数是传动部分的振动。故当频率较低时，驱动部分容易发生共振。

(2)各构件的振动中，摆杆由于是细长结构最容易发生弯曲振动，压电堆同样容易发生弯曲振动；活齿架由于具有复杂结构，故其振型既有弯曲振动又有旋转振动；活齿振型主要以轴向振动为主；中心轮振型主要是弯曲振动。

表1　电机部分固有频率及振型

4.2谐响应分析

当对压电堆所加的电压激励频率接近电机固有频率时，电机各构件会被激发出各种振动模态。假设单位节点向量满足

δm=Φq

(14)

Φ=[φ1φ2…φn]

q=(q1(t)，q2(t)，…，qn(t))T

式中，Φ为n个振动模态特征向量矩阵；q为n个正交模态对应的模态坐标。

将式(14)代入式(13)并归一化，可得到谐响应矩阵方程如下：

对单级放大机电集成压电谐波电机进行谐响应分析，设定激励频率最大值和最小值分别为fmax= 22 000 Hz、fmin= 1600 Hz，由激励频率范围确定求解步长ΔΩ=2π[(fmax-fmin)/n]，取n=100。图9和图10分别给出了电机部分构件的振动位移响应和应力响应曲线。由图9、图10可知：

(a)活齿架端面位移响应

(b)中心轮端面位移响应

(c)活齿啮合面位移响应

(d)摆杆柱面位移响应图9　电机主构件振动位移响应曲线

(a)活齿架接触面应力响应

(b)中心轮接触面应力响应

(c)活齿接触面应力响应

(d)摆杆接触面应力响应图10　电机主构件应力响应曲线

(1)各构件在x轴、y轴和z轴三个方向均有比较明显的振动位移，其中活齿、活齿架、中心轮的最大振动位移发生在沿x轴方向，摆杆最大振动位移发生在沿z轴方向。

(2)各构件发生明显共振的频率点主要分布在8272 Hz、14 512 Hz和19 088 Hz附近；不同构件最大振动位移对应的频率不同，活齿、活齿架、中心轮发生在19 088 Hz处，摆杆发生在8272 Hz处，这与前文模态振型分析是一致的，驱动部分在低频处容易共振，传动部分共振发生在高频处。

(3)随着频率的变化，不同构件最大共振位移及其方向是不相同的；在8272 Hz频率点处，活齿架、活齿、摆杆的最大共振位移出现在沿z轴方向，中心轮最大共振位移出现在x轴方向；在19 088 Hz频率点处，各构件最大共振位移均发生在沿x轴方向。

(4)发生较大应力响应的频率点主要分布在8272 Hz、14 512 Hz和19 088 Hz附近，这与位移响应是一致的;且在8272 Hz频率点时，活齿架和摆杆的应力都达到最大值，在19 088 Hz时，中心轮和活齿的应力出现最大值。

(5)各构件最大应力在8272 Hz时发生在活齿架接触面处，这是由于活齿架上的孔较大而容易发生应力集中现象。

5实验验证

对波发生器输出位移进行实验验证，如图11所示，激光测振仪采用德国OptoMET公司生产的Vector系统，是一种能够同时输出位移、速度及加速度的激光测试装置。压电驱动电源是一种采用XMT的多通道驱动设备，信号发生器是一种自制的可调控多信号发生装置，控制器能够将激光测振仪采集的信号进行处理,然后显示在计算机上。分别对压电叠堆施加3 Hz和50 Hz的正弦信号，得到波发生器的摆动波形如图12所示。

图11　实验测试系统

将图12中测试位移的电压单位按照每2V对应0.5mm转换成长度单位，可得输入信号为3Hz和50Hz时对应的输出位移分别为0.333mm和0.349mm，与第2节中理论位移0.365mm分别相差8.9%和4.4%。

对样机的输出转矩也进行了实验测试，但是输出转矩只达到0.5N·m，与目标转矩差距较大，目前正在对电机进行调试。造成输出转矩较小的原因主要有：①各零件的加工精度没有达到要求，造成装配误差较大；②由于摆杆所受的前后和左右两方向的力存在相互影响，使得波发生器输出力减小。针对出现的问题，目前正在寻求高精度数控机床进行关键零件的加工制造；对于两方向力相互影响的问题，目前正在寻找最优改进策略。

(a)3 Hz测试曲线

(b)50 Hz测试曲线图12　波发生器输出位移测试曲线

6结论

设计了一种单级放大机电集成压电谐波电机，阐述了该种电机的工作原理，给出了其设计方法及尺寸选择。推导了电机最大应力公式，并通过仿真验证了理论值。分析了电机的固有频率和振型以及电机在简谐激励下的位移和应力响应。结果表明：①活齿所受最大应力理论值与仿真值相差4.04%；②驱动构件在低频时容易共振，传动构件在高频时容易共振；③在激励作用下，活齿振动位移最大，活齿架应力集中最为严重。研究结果为单级放大机电集成压电谐波电机的改进和实验提供了理论基础。

参考文献：

[1]鹿存跃，赵淳生．采用耦合机构驱动的压电电机的研究进展[J]．中国机械工程，2003, 14(7): 626-629.

LuCunyue,ZhaoChunsheng.NewDevelopmentofPiezoelectricMotorwithCouplingMechanism[J].ChinaMechanicalEngineering, 2003, 14(7): 626-629.

[2]邢继春，许立忠．旋转惯性压电电机最优驱动方案分析[J]．中国机械工程，2014, 25(18): 2451-2455.

XingJichun,XuLizhong.AnalysisofOptimalDrivingofRotaryIntertialPiezoelectricMotor[J].ChinaMechanicalEngineering, 2014, 25(18): 2451-2455.

[3]ToyamaS.SphericalUltrasonicMotorforPipeInspectionRobot[C]// 7thInternationalConferenceonOptimizationoftheMechanicalEngineering,ManufacturingSystems,RoboticsandAerospace,OPTIROB2012.Mamaia,Romania, 2012： 3-11.

[4]TomoakiM.MicroUltrasonicMotorUsingaOneCubicMillimeterStator[J].SensorsandActuatorsA:Physical, 2014, 213: 102-107.

[5]朱鹏举，时运来，赵淳生．一种新型大推力直线压电作动器[J]．振动、测试与诊断，2015, 35(1): 163-169.

ZhuPengju,ShiYunlai,ZhaoChunsheng.ANewTypeofLarge-thrustLinearPiezoelectricActuator[J].JournalofVibration,Measurement&Diagnosis, 2015, 35(1): 163-169.

[6]张海峰，赵爱玲，李立．一种高效压电旋转驱动器的设计和研究[J]．压电与声光，2014, 36(6): 991-998.

ZhangHaifeng,ZhaoAiling,LiLi.DesignandResearchofaHighlyEfficientPiezoelectricRotaryActuator[J].Piezoelectrics&Acoustooptics, 2014, 36(6): 991-998.

[7]ChenW,LiuY,YangX,etal.Ring-typeTravelingWaveUltrasonicMotorUsingaRadialBendingMode[J].IEEETransactionsonUltrasonics.Ferroelectrics,andFrequencyControl, 2014, 61(1): 197-202.

[8]BarthO.HarmonicPiezodrive-miniaturizedServoMotor[J].Mechatronics, 2000, 10(4)： 545-554.

[9]辛洪兵，郑伟智．压电谐波电机的研究[J]．压电与声光，2004, 26(2): 122-125.

XinHongbing,ZhengWeizhi.StudyonHarmonicPiezomotor[J].Piezoelectrics&Acoustooptics, 2004, 26(2): 122-125.

[10]王长明, 阳培, 张立勇．谐波齿轮传动概述[J] ．机械传动，2006, 30(4): 86-88.

WangChangming,YangPei,ZhangLiyong.SummaryofStatusontheHarmonicGearDrivingTechnology[J].JournalofMechanicalTransmission, 2006, 30(4): 86-88.

[11]XuLizhong,LiHuaiyong.AnElectromechanicalIntegratedHarmonicPiezodriveSystem[J].JournalofMechanicalDesign,ASME, 2014, 136(3): 034502.

[12]XuLizhong,LiChong.CoupledDynamicsforanElectromechanicalIntegratedHarmonicPiezodriveSystem[J].ArabianJournalforScienceandEngineering, 2014, 39(2): 9137-9159.

(编辑苏卫国)

Design and Simulation of a Single Amplification Electromechanical Integrated Harmonic Piezoelectric Motor

Gao LichaoXu LizhongLi Chong

Yanshan University, Qinhuangdao， Hebei, 066004

Abstract:A single amplification electromechanical integrated harmonic piezoelectric motor was designed, and the working principles were illustrated. Besides, the design procedure, continuous transmission conditions and principles of parameter selection were given. For the failure regions existed in the motor, the maximum stress equation was deduced and was verified by comparing with FEM results. In addition, the natural frequencies, modal shape and displacement and stress response under excitation were analyzed. Results show, the maximum stress is as 45.54 MPa, and the difference is only 4.04% comparing with FEM results. Under the action of incentive, the vibration displacement of movable tooth is largest, and stress concentration on tooth carrier is most serious.

Key words:single amplification; harmonic piezoelectric motor; maximum stress; FEM simulation

收稿日期：2015-06-26

基金项目：国家自然科学基金资助项目(51275441)

中图分类号：TH122；TM356

DOI：10.3969/j.issn.1004-132X.2016.10.002

作者简介：高立超，男，1990年生。燕山大学机械工程学院硕士研究生。研究方向为单级放大机电集成压电谐波电机。许立忠(通信作者)，男，1962年生。燕山大学机械工程学院教授、博士研究生导师。李冲，男，1988年生。燕山大学机械工程学院博士研究生。