电动车辆组合式离合器换挡过程优化控制
李军求 陈建文 王宜河 王义政


摘要:针对装配组合式离合器的两挡行星变速器电动车辆的换挡问题,建立了换挡过程动力学模型,选取冲击度和滑摩功作为综合控制目标,考虑换挡过程驱动电机转矩和变速器输出端阻力矩的变化,建立组合式离合器摩擦转矩线性二次型最优控制模型,得到油压最优控制轨迹.选取电机不同油门开度和路面坡道工况,仿真分析了两挡行星变速箱降挡的控制过程.结果表明,所得到的最优轨迹可以有效提高车辆的换挡品质,且换挡品质对电机转矩的变化较变速器输出端阻力矩的变化更为敏感.
关键词:电动车辆;组合式离合器;动力学模型;线性二次型最优控制;换挡品质
中图分类号:U463.2 文献标识码:A
文章编号:1674-2974(2016)02-0022-06
离合器换挡具有高效率、可灵活控制等特点,在车辆上的应用越来越广泛[1].换挡过程中应控制换挡冲击和滑摩功,两者均受离合器摩擦转矩影响,在离合器几何结构一定时,摩擦转矩由油压特性决定.因此离合器油压特性研究对改善换挡品质有重要意义.
最优控制理论在换挡品质优化中得到了广泛应用[2-7],其中线性二次型、动态规划、粒子群、模糊控制等算法对于改善变速箱离合器结合过程中冲击度和滑摩功都取得了良好的应用效果,其中较为典型的是丰田公司A350E自动变速器,采用线性二次型最优伺服控制器实现两个制动器转速同步控制,具有较好的工程应用价值,尤其是电动汽车在换挡过程中驱动电机相比发动机调速更为迅速,效果更为显著.本文针对电动车辆组合式离合器换挡的两挡变速器,对降挡过程进行分析,利用线性二次型最优控制理论获得不同坡度下离合器油压最优控制轨迹,使车辆获得良好的换挡品质.
1系统组成及工作原理
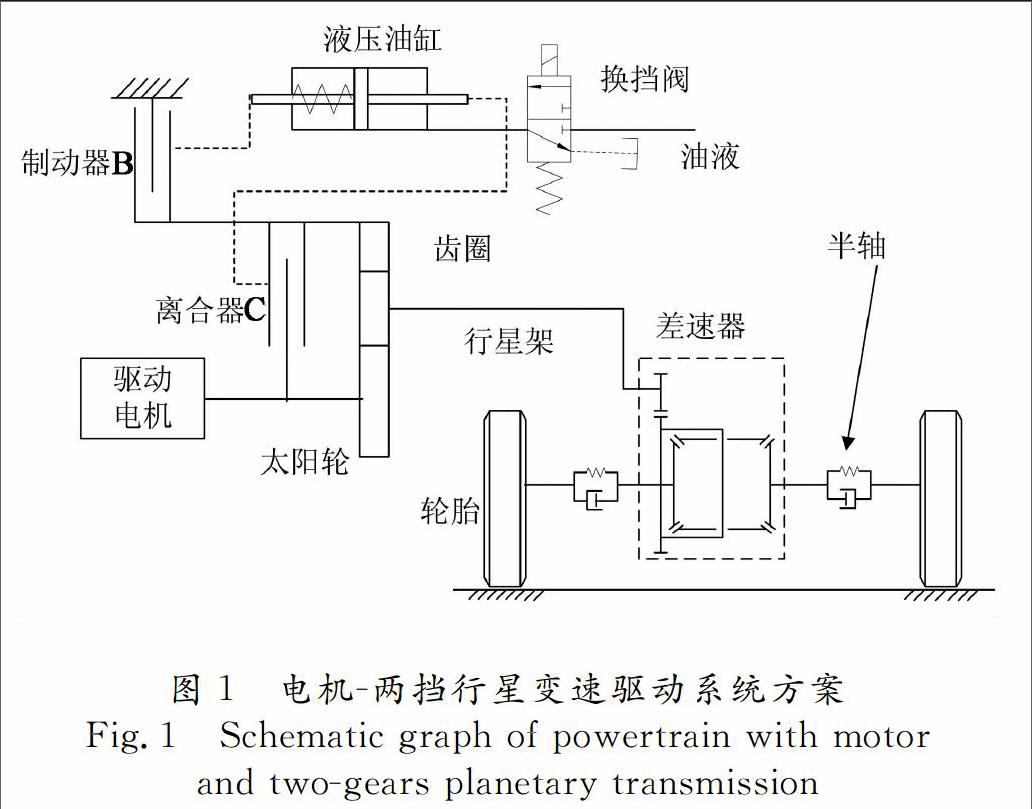
变速驱动系统方案如图1所示,由电机与两档行星自动变速箱组成,其中离合器C和制动器B为组合式离合器,完成高低挡切换,由单一液压油缸、回位弹簧和换挡阀完成操控,结构上实现离合器、制动器联动控制,油压直接作用对象为液压油缸活塞.
降挡时,换挡阀充油油路打开,液压油缸充油,控制油压增大,推动油缸活塞使得离合器C分离,经过短时的自由阶段(离合器和制动器均处于分离)后,油缸活塞压紧制动器摩擦片,制动器接合,使两挡行星变速器处于低挡状态,传动比为1+k,k为齿圈齿数与太阳轮齿数之比.升挡时,换挡阀泄油油路打开,制动器油缸卸油,控制油压下降,在回位弹簧的作用下,制动器分离,经过短时自由阶段,油缸活塞压紧离合器摩擦片离合器接合,使两挡行星变速器处于高挡状态,传动比为1.
2组合式离合器换挡动力学模型
忽略变速箱中轴、轴承及齿轮啮合的弹性与阻尼,将各元件视为刚性无阻尼惯性元件,并以集中质量形式表示,这些简化对换挡过程动力学分析不会产生太大影响[8],由此得到采用组合式离合器换挡的两挡行星变速器动力学模型如图2所示.图中,Tm为电机转矩,Tf为变速器输出端阻力矩,Tcl与Tbr分别为离合器与制动器传递转矩,J1为电机惯量, J2为整车平移质量等效惯量,太阳轮、齿圈、行星架和行星轮的转动惯量、转速、质量分别以下标s,r,c,p加以区别.
3换挡品质最优控制模型
本文以上坡降挡工况为例,进行换挡过程最优控制,并假设换挡过程中变速器输出端阻力矩保持定值,输入端力矩由电机油门开度确定.
3.1换挡综合评价指标构建
离合器换挡过程主要有两个控制指标,即离合器结合平稳和使用寿命,分别由冲击度和滑摩功来评价.换挡过程中冲击度越大,车上乘员舒适性越差,此外过大的冲击度对车辆传动系部件也会造成不良影响,因此需将冲击度控制在一定范围之内.冲击度j定义为车辆纵向加速度的变化率,即:
换挡过程非常短暂,实际应用将不同工况下最优轨迹进行函数拟合,拟合系数保存在车辆控制系统内存.在线控制时,通过查表和插值获得拟合系数,从而迅速得到最优轨迹[9].
4仿真分析
车辆上坡时,当车速降到一定数值(本文设定为25km/h)后开始换挡.假设降挡时油门开度保持不变,最优控制时选取η=0.5.本文仿真对象为某电动车辆,参数见表1.为了对比分析干扰矩阵对换挡品质的影响,对不同油门开度α、不同路面坡度i的最优控制和无最优控制工况进行了仿真,结果如图3-图8所示.
无最优控制的油压变化如下:第一阶段组合式离合器快速充油,使离合器C分离阶段时间短,该阶段出现第一个大冲击度;第二阶段油液推动油缸活塞运动,离合器和制动器均不传递转矩,产生动力中断;第三阶段为制动器B滑摩启动状态,这是瞬间过渡状态,液压油缸无体积变化,摩擦片贴合,压力升高,开始产生制动器摩擦力矩,由于缸内压力升高,使摩擦力矩瞬间增大,过渡到滑磨阶段,形成第二个大冲击度;第四阶段制动器开始滑摩,随着油压的升高,制动器滑摩速度绝对值逐渐减小直至为0,在制动器完全接合的瞬间,制动器实际转矩变为静摩擦力矩,使得出现第三个大冲击度,如图3和图4所示.
组合式离合器在不加控制时活塞油压完全由液压系统结构决定,在不同油门开度和路面坡度时油压特性相同,如图3中曲线1所示.因此,随着油门开度和路面坡度的增加,只能通过增加换挡时间来满足换挡所需的摩擦力矩,并且油门开度对换挡时间的影响更为显著,如图5所示.图中曲线1为系统摩擦力矩储备,即在系统最大油压下的系统的储备静摩擦转矩,在离合器分离阶段前指离合器转矩,在制动器结合后指制动器转矩.由图5可知,当油门开度和路面坡度改变时,系统摩擦转矩均在摩擦力矩储备范围内.
通过对组合式离合器油压进行最优控制,并通过合理调整离合器分离时间,可以实现不同工况下换挡时间一致,如图3中2,3,4所示曲线.图6中在控制滑摩功的同时,合理减小该阶段的冲击度,且将自由阶段控制在极短时间内,有效减小了换挡过程的动力中断,并消除了滑摩启动状态,这使得在组合式离合器进入制动接合阶段时换挡平稳性得到很大提升.在制动器接合阶段主从部分转速差接近0时,调节油压使得制动器的实际传递转矩接近于由动力学模型决定的静摩擦力矩,减小该瞬时的冲击度.根据换挡时摩擦元件的滑磨时间在0.5~1.5 s较为适宜[10],图7说明了通过油压合理控制,各工况下换挡时间控制为0.63 s,最大的冲击度为6.3 m/s3,满足冲击度控制标准j<10 m/s3.图8进一步说明了在离合器分离和制动器结合阶段,通过最优控制电机和齿圈转速变化更为平缓.
降挡过程中各种情况下滑摩功和冲击度见表2.
表2进一步说明:油门开度和道路坡度相同时,最优控制时的冲击度和滑摩功均小于无控制情况,且上述2种情况下冲击度和滑摩功都随电机转矩和负载转矩的增加而增大,其中负载阻力增大时,即坡度从5%变化为10%而油门开度都维持50%,最大冲击度增加相对量较小,其中无控制时最大冲击度从49.6 m/s3增加到62 m/s3,最优控制时从3.3 m/s3增加到了3.8 m/s3,变化范围为15%~25%;但是电机转矩增大时,即油门开度从50%增加到80%而坡度都维持10%,无控制时最大冲击度从62 m/s3增加到105.4 m/s3,有最优控制时从3.8 m/s3变为6.3 m/s3,变化范围为65%~70%,且滑摩功变化不明显,冲击度对电机转矩变化更为敏感,其依据是降挡时电机转矩变化通过变速箱减速增扭作用扩大了1+k倍,因此对冲击度影响更为显著.
5结论
1)系统进行最优控制时,通过调整油压变化和换挡时间,有效地控制了系统冲击度,同时降低了换挡滑摩功.这使冲击度和滑摩功得到了较好的平衡,有效地提高了换挡品质,为解决自动变速器的换挡控制问题提供了一种有效方法.
2)在考虑干扰矩阵的情况下,当电机转矩和路面坡度改变时,滑摩功变化很小,但是冲击度变化明显,且对电机转矩的变化更加敏感.电机转矩较大时,冲击度和滑摩功较大.
参考文献
[1]GAO Bing-zhao, CHEN Hong, LIU Qi-fang, et al. Clutch slip control of automatic transmissions: a nonlinear feedforward-feedback design[C]//Proceedings of 2010 IEEE International Conference on Control Applications. New York: IEEE, 2010:884-889.
[2]HAJ-FRAJ A, PFEIFFER F. A model based approach for the optimization of gearshifting in automatic transmissions [J]. International Journal of Vehicle Design, 2002, 28(1/3):171-188.
[3]SONG X Y, ZULKEFLI M A M, SUN Z X, et al. Automotive transmission clutch fill control using a customized dynamic programming method [J]. Journal of Dynamics Systems, Measurement, and Control, 2011, 133(5): 1-9.
[4]顾强,程秀生. 基于粒子群算法的电动汽车DCT 升档动力协调控制[J]. 农业工程学报, 2012,28(8):84-90.
GU Qiang, CHENG Xiu-sheng. Coordinated control of upshift power of double clutch transmission for electric vehicle based on particle swarm optimization[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012,28(8):84-90.(In Chinese)
[5]SUN Cheng-shun, ZHANG Jian-wu. Optimal control applied in automatic clutch engagements of vehicles[J]. Chinese Journal of Mechanical Engineering,2004,17(2): 280-283.
[6]张飞铁,周云山,薛殿伦. CVT 起步离合器模糊控制算法研究[J]. 湖南大学学报:自然科学版,2006,33(5):57-60.
ZHANG Fei-tie, ZHOU Yun-shan, XUE Dian-lun. Research on fuzzy control algorithm of CVT starting clutch[J]. Journal of Hunan University: Natural Sciences, 2006,33(5):57-60.(In Chinese)
[7]GLIELMO L, VASCA F. Optimal control of dry clutch engagement[R]. No.2000-01-0837. Washington, DC: SAE International, 2000.
[8]孙文涛, 陈慧岩, 伍春赐. 电控自动变速器换挡过程自适应控制策略[J]. 机械工程学报, 2009, 45(1):293-299.
SUN Wen-tao, CHEN Hui-yan, WU Chun-ci. Shifting process adaptive control strategy with electronic automatic transmission [J]. Journal of Mechanical Engineering, 2009, 45(1) :293-299. (In Chinese)
[9]秦大同,陈清洪. 基于最优控制的AMT/DCT离合器通用起步控制[J]. 机械工程学报, 2011, 47(12) :85-91.
QIN Da-tong, CHEN Qing-hong. Universal clutch starting control of AMT/DCT automatic transmission based on optimal control [J]. Chinese Journal of Mechanical Engineering,2011, 47(12) :85-91. (In Chinese)
[10]马彪, 孙宪林, 剧引芳. 车辆自动换档离合器缓冲控制方法分析[J]. 兵工学报, 1996(2):47-53.
MA Biao, SUN Xian-lin, JU Yin-fang. Anaysis of buffering control of vehicle automatic shift clutch [J]. Acta Armamentarii, 1996(2): 47-53.(In Chinese)

