Stewart六自由度并联平台动力学模型振动分析

钱承　鄂加强　刘明　邓元望　朱浩

摘要：为提高Stewart六自由度并联减振平台控制精度，采用力学分析、旋转矩阵等方法构建了减振平台的速度特性和加速度特性等动力学分析模型和Adams虚拟样机模型，并对该平台在瞬态激励下上端载物平台的位移输出情况、速度情况和加速度情况以及固有特性进行了振动仿真分析.结果表明：1）上端平台的响应较小，最大的位移出现在0.7 s左右且能够很快地保持稳定；2）Stewart六自由度并联平台的一阶固有频率较小，低频特性较好，且在大范围的频率段范围内响应稳定.

关键词：Stewart并联平台；动力学分析；振动仿真；固有特性

中图分类号：TH113 文献标识码：A

文章编号：1674-2974（2016）02-0036-07

Stewart六自由度并联平台最初是由德国学者Stewart[1]提出的，相比串联机构其有以下优点：具有高刚度且结构比串联式稳定；并联机构定位准确，承载能力强，动态特性好；在实时计算控制时，并列式结构反解容易实现.Stewart六自由度并联平台从诞生以来其各种形式及结构被广泛用于减振及精确定位领域[2-4].由于Stewart平台结构的复杂性，国内外学者对其运动学和动力学特性进行了广泛研究[5-9].Afzali-Far等人[10]研究了对称式结构的Stewart并联平台的阻尼减振控制，并设计和研究了Stewart的动力学特性.Zhao等人[11]研究了并联平台的逆向运动学和刚体动力学特性，通过仿真平台得到了平台的速度、加速度、力矩等特性.

Stewart六自由度并联平台的运动学及动力学分析是后续结构优化及控制器设计的基础，因此研究其运动学及动力学理论具有重要的意义.目前针对Stewart平台的动力学模型分析方法主要有拉格朗日法[12-14]（Lagrange）和牛顿欧拉法[15-16]（Newton-Euler）两种.其中，拉格朗日法只需计算系统的动能和势能就能确定系统的动力学特性，因此该方法相对比较简单且有利于控制策略的制定.

本文针对所设计的Stewart六自由度并联平台进行了运动学和动力学分析，并在此基础上通过Adams软件建立了模型的动力学模型及振动模型，分析Stewart六自由度并联平台动力学模型振动特性，为提高Stewart六自由度并联减振平台控制精度提供理论与技术支持.

1Stewart六自由度并联平台力学分析

1.1Stewart六自由度并联平台结构

Stewart六自由度并联平台主要由负载平台、基平台和六根驱动杆组成，每根驱动杆通过铰接方式分别连接负载平台和基平台.根据铰接方式的不同可以分为球铰连接（Spherical joint）SPS型和万向铰连接（Universal joint）UPS型；根据驱动杆与负载平台和基平台的连接点数又可分为3-3型Stewart平台，3-6型Stewart平台及6-6型Stewart平台.

应用最为广泛的Stewart平台为驱动杆与负载平台和基平台都有6个连接点数的UPS型平台，即6-UPS型Stewart六自由度并联平台，其结构简图如图1所示.

1.2旋转矩阵的确定

为详细有效地对Stewart六自由度并联平台进行运动学分析，在图1所示的结构图上建立了两个坐标系，即静止坐标系{B，x，y，z}，其原点固定在基平台的几何中心，动坐标系{P，x1，y1，z1}，其原点固定在负载平台的几何中心.定义驱动杆和负载平台的铰接点为Pi （i=1，2，…，6），与Pi相对应的驱动杆和基平台的铰接点为Bi （i=1，2，…，6）.

2Stewart六自由度并联仿真平台动力学研究

2.1Stewart六自由度并联机构虚拟样机建立

本文所研究的三维实体模型如图3所示，模型由上端负载平台、底端基平台以及6根压电驱动杆组成.该平台的特征参数为：上端载物平面直径为250 mm，下端平面直径为350 mm，上下平面之间的距离为330 mm.其中驱动杆和上下两平台通过万向铰连接.

根据Adams对三维软件的需要，将Pro/E中的三维实体另存为Parasolid格式，为了两个对接软件单位的统一，在Pro/E输出Parasolid格式时将单位设置成MMKS.将保存的Parasolid格式文件导入Adams软件进行虚拟样机的构建.为了降低平台的质量，模型采用钛合金材料，其材料密度ρ=4 850 kg/m3，弹性模量E=1.02×105 MPa，泊松比PRXY=0.3.

为了仿真的方便并满足软件对模型的需要，对模型进行了一系列简化，包括构件的合并、细小特性单元的删除等.根据设计原理，在驱动杆和上下两平台之间的万向铰通过建立2个旋转副实现其功能；驱动杆的上下两部分之间通过平移副连接，并根据驱动杆的设计原理添加了弹簧和阻尼单元，以实现减振的目的.由于本Stewart六自由度平台运用在无重力环境下，因此在Adams中取消了重力单元.为了约束的需要及和实际使用时具有相同的条件，在下平台和地之间通过一个Bushing单元连接，考虑到实际运用中是固定的，所以将Bushing单元的刚度设置得比较大，该单元可以同时传递力与力矩.为了研究下端平台的扰动对上端载荷平台的影响，在下端平台底端建立了扰动力，在仿真初始时刻施加垂直于底端向上的1 N的力STEP（ time，0，1，1，0），其形式如图4所示.

2.2 Stewart六自由度并联机构动力学仿真结果

将上节所建立的动力学仿真模型进行仿真分析，设置仿真时间为10 s，仿真500步.针对该扰动力，上端平台的位移响应、速度响应及加速度响应如图5所示.根据动力学仿真结果图可以看出，上端平台的响应较小，最大的位移出现在0.7 s左右且能够很快地保持稳定.

图6所示为6根驱动杆在收到扰动后所受到的力.由图6可看出，6根驱动杆在收到扰动的干扰后，分别输出了相应的力以对抗扰动对上端平台的影响，且在3 s后能快速保持稳定.

图中，最上面的两条线中，曲线1为作动器1的输出力，曲线2为作动器2的输出力；中间两条线中，曲线3和曲线4分别为作动器3和4的输出力；最下面两条线中，曲线5和曲线6分别为作动器5和6的输出力.从仿真分析可以得出，Stewart六自由度并联平台的动力学特性比较稳定，在有扰动的情况下能及时、快速地恢复稳定状态.

3Stewart六自由度并联平台的振动仿真

3.1Stewart六自由度振动仿真平台建立

为得到Stewart六自由度并联平台的振动特性，在Adams中调用Vibration模块，建立了振动仿真平台.Adams/Vibration是在频率域上求解系统特性的模块，且可以计算仿真平台不同位置的振动特性，可以采用自由振动及强迫振动的方式.本文中采用了强迫振动的方式对平台进行振动特征的求解，在底端平面建立振动的输入激励，分别为x，y，z方向的简弦力，通过扫频的方式进行计算，即激励的幅值不变，而激励的频率不断增大，其激励的方程式可写为式（34）.

同时在上端平面建立振动模型的输出，同样也为x，y，z方向.建立完输入和输出通道后设置仿真参数，本文设置激励的幅值为1 N，初始相位角为0°，扫频范围为0.1～100 Hz，计算步骤为2 000步.其仿真步骤如图7所示.

3.2Stewart六自由度振动仿真结果分析

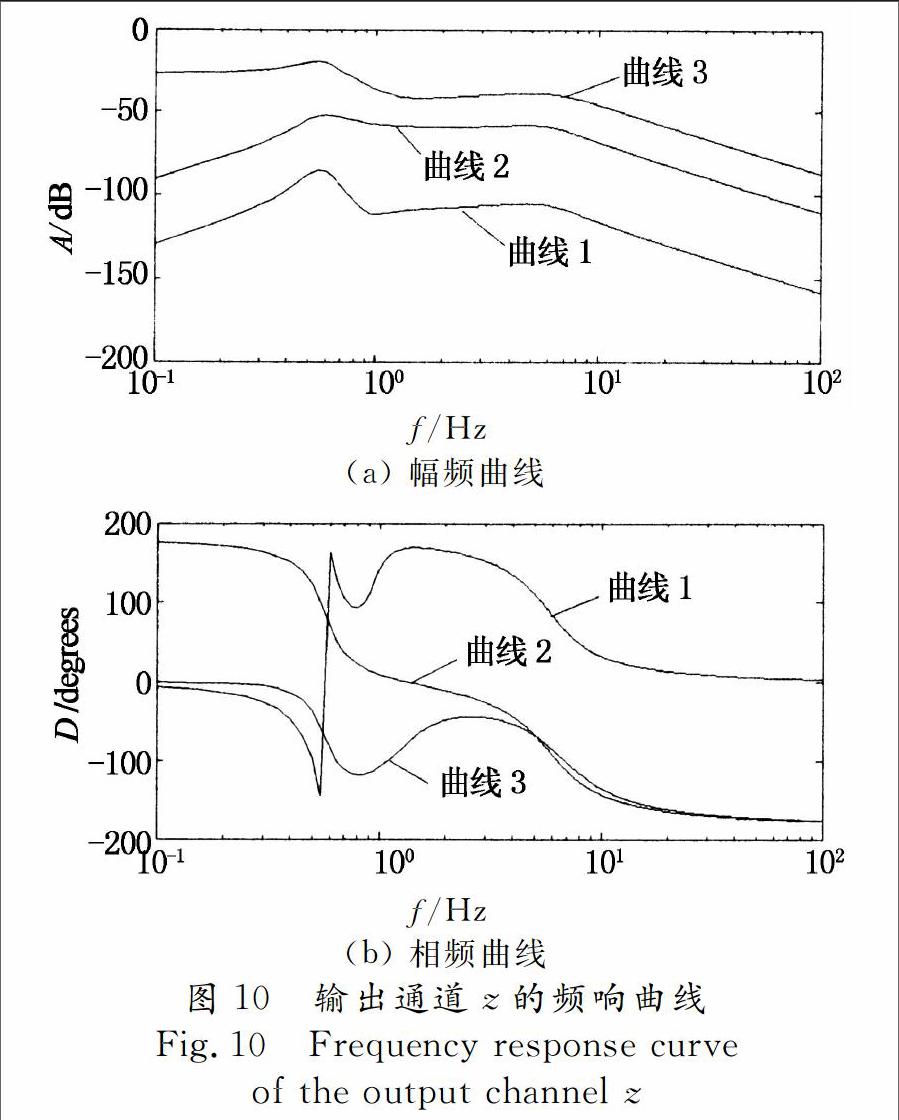
经过振动仿真，得出了系统输入和输出之间的频响特性，其结果如图8-图10所示分别为3个输入通道的激励对3个输出通道x，y和z的频响曲线.

图8中，曲线1代表当输入为x方向的激励时输出x方向的频响特性；曲线2代表当输入为y方向的激励时输出x方向的频响特性；曲线3则代表当输入为z方向的激励时输出x方向的频响特性.

图9中，曲线1、曲线2、曲线3分别代表了输入为x，y，z方向激励时输出y方向的频响曲线.

图10中，曲线1、曲线2、曲线3分别代表输入为x，y，z方向激励时输出z方向的频响曲线.

由图8-图10的频响曲线图可以看出，Stewart六自由度并联平台的一阶固有频率在0.6 Hz左右，具有较低的固有频率，且在100 Hz的频率范围内响应平稳，表明了Stewart六自由度并联平台具有较宽的工作频率范围.表1给出了本文所研究的Stewart六自由度并联平台的前5阶模态参数的仿真结果.

通过表1可以看出一阶模态的固有频率为0.572 06 Hz，和频响曲线的结果相同，且从表1中可以看出前三阶的固有频率值比较靠近，从4阶模态开始固有频率变为6 Hz.因此可以看出Stewart六自由度并联平台的固有频率较低，具有较好的低频特性.

4结论

1） 分析了Stewart六自由度并联平台的运动学及动力学特性，并以Adams软件搭建了相应的仿真平台.在下端面建立了幅值为1 N的扰动力，进行了模型的动力学仿真.结果显示，本文建立的虚拟样机很好地模拟了Stewart六自由度并联平台的工作状况.

2） 为进一步分析Stewart六自由度并联平台的动力学固有特性，调用Adams/Vibration模块，在下端平台建立了系统的输入通道，在上端平台建立了系统的输出通道，仿真分析了系统输入通道和输出通道之间3个方向的频响特性.结果显示了3个方向的频响曲线且计算得出了前5阶模态参数，从数据中可以看出Stewart六自由度并联平台的一阶固有频率较小，具有较好的低频特性且在大范围的频率段内，响应稳定.

参考文献

[1]STEWART D. A platform with six degrees of freedom [J]. Proceedings of the Institution of Mechanical Engineers， 1965， 180： 371-386.

[2]PREUMONT A， HORODINCA M， ROMANESCU I， et al. A six-axis single-stage active vibration isolator based on Stewart platform [J]. Journal of Sound and Vibration， 2007， 300（3）： 644-661.

[3]KAMESH D， PANDIYAN R， GHOSAL A. Modeling， design and analysis of low frequency platform for attenuating micro-vibration in spacecraft[J]. Journal of Sound and Vibration， 2010， 329（17）： 3431-3450.

[4]AZADI M， FAZELZADEH S A， EGHTESAD M， et al. Vibration suppression and adaptive-robust control of a smart flexible satellite with three axes maneuvering [J]. Acta Astronautica， 2011， 69（5/6）： 307-322.

[5]E Jia-qiang， QIAN Cheng， LIU Teng， et al. Research on the vibration characteristics of the new type of passive super static vibratory platform based on the multi-objective parameter optimization[J]. Advances in Mechanical Engineering， 2014， 2014： 1-8.

[6]LOPES A M. Dynamic modeling of a Stewart platform using the generalized momentum approach [J]. Communications in Nonlinear Science & Numerical Simulation， 2009， 14（8）： 3389-3401.

[7]STAICU S. Dynamics of the 6-6 Stewart parallel manipulator [J]. Robotics and Computer-Integrated Manufacturing， 2011， 27（1）： 212-220.

[8]MUKHERJEE P， DASGUPTA B， MALLIK A K. Dynamic stability index and vibration analysis of a flexible Stewart platform [J]. Journal of Sound and Vibration， 2007， 307（3/5）： 495-512.

[9]ZHOU Wan-yong， CHEN Wu-yi， LIU Hua-dong， et al. A new forward kinematic algorithm for a general Stewart platform[J]. Mechanism and Machine Theory， 2015， 87： 177-190.

[10]AFZALI-FAR B， LIDSTRM P， NILSSON K. Parametric damped vibrations of Gough-Stewart platforms for symmetric configurations[J]. Mechanism and Machine Theory， 2014， 80（4）： 52-69.

[11]ZHAO Yong-jie， QIU Ke， WANG Shuang-xi， et al. Inverse kinematics and rigid-body dynamics for a three rotational degrees of freedom parallel manipulator[J]. Robotics and Computer-Integrated Manufacturing， 2015， 31： 40-50.

[12]HARIB K， SRINIVASAN K. Kinematic and dynamic analysis of Stewart platform-based machine tool structures[J]. Robotica， 2003， 21（9）： 541-554.

[13]DASGUPTA B， MRUTHYUNJAYA T S. A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator[J]. Mechanism and Machine Theory， 1998， 33（8）： 1135-1152.

[14]JI Z M. Dynamics decomposition for Stewart platforms [J]. ASME Journal of Mechanical Design， 1994， 116（1）： 67-69.

[15]GENG Z， HAYNES L S， LEE J D， et al. On the dynamic model and kinematic analysis of a class of Stewart platforms [J]. Robotics and Autonomous Systems， 1992， 9： 237-254.

[16]XU Yu-fei， LIAO He， LIU Lei， et al. Modeling and robust H-infinite control of a novel non-contact ultra-quiet Stewart spacecraft[J]. Acta Astronautica， 2015， 107： 274-289.