自适应最稀疏时频分析方法的分解能力研究

李宝庆 程军圣　吴占涛　杨宇

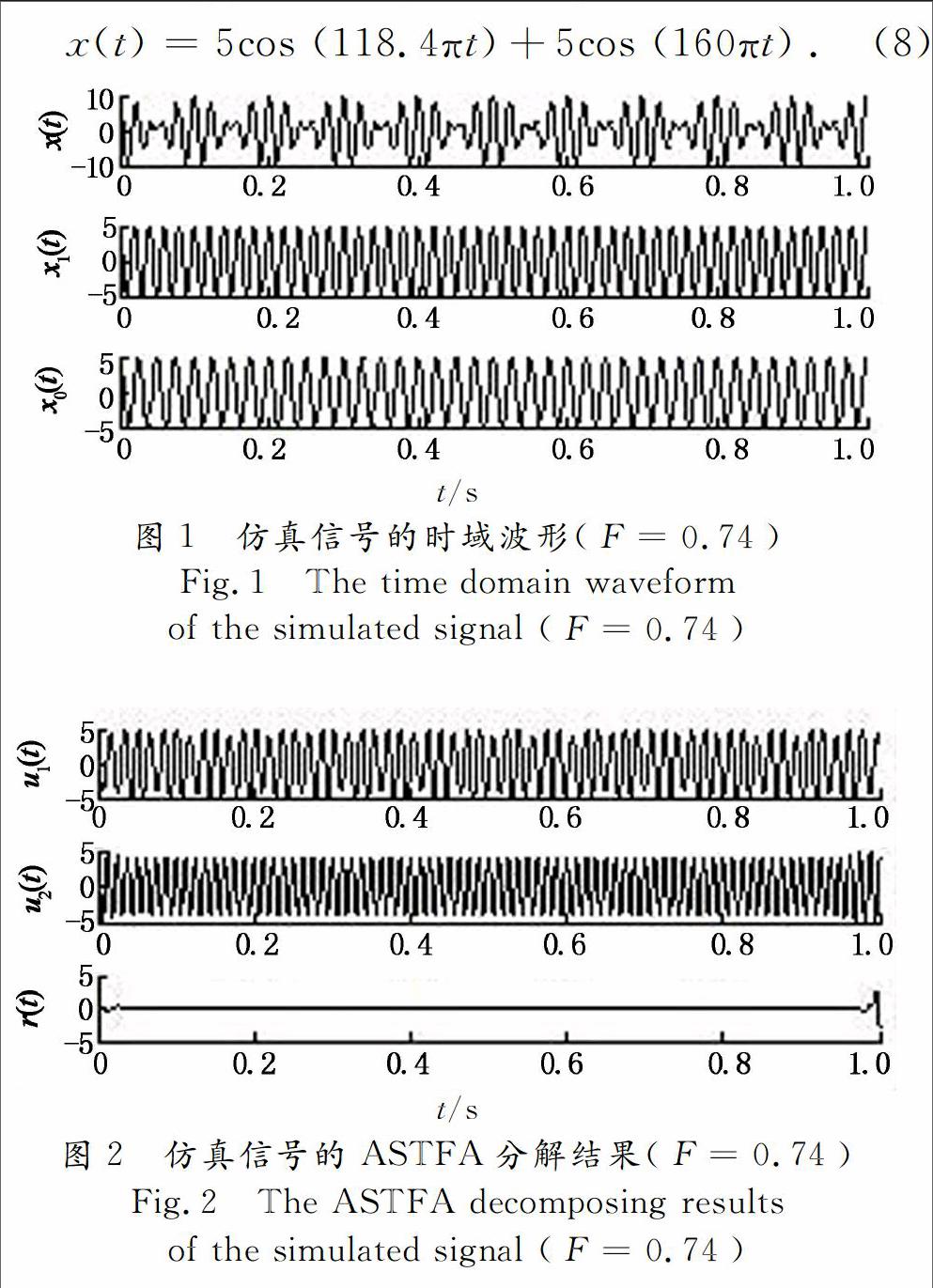
摘要：自适应最稀疏时频分析（adaptive and sparsest time-frequency analysis，ASTFA）方法将信号分解转化为最优化问题，在优化的过程中实现信号的自适应分解.为了研究ASTFA的分解能力，在定义分解能力评价指标（Evaluation Index of Decomposition Capacity，EIDC）的基础上，以双谐波分量合成信号模型来研究幅值比、频率比、初始相位差对ASTFA的影响.同时，将ASTFA方法与经验模态分解（Empirical Mode Decomposition， EMD）、局部特征尺度分解（Local Characteristic-scale Decomposition， LCD）进行对比分析.研究结果表明，ASTFA方法的分解能力基本不受幅值比的影响，可分解的极限频率比较大，不受初始相位差的影响，该方法的分解能力具有明显的优越性.

关键词：自适应最稀疏时频分析；经验模态分解；局部特征尺度分解；分解能力；相位

中图分类号：TH113.1； TN911.7 文献标识码：A

文章编号：1674-2974（2016）02-0043-05

自适应时频分析方法可以在对信号分解的过程中根据信号本身的特性自动选择基函数或者其参数，从而实现信号的分解.目前广泛应用的自适应时频分析方法有EMD方法，EMD通过多次迭代将信号分解为一系列具有不同时间尺度的内禀模态函数（Intrinsic Mode Function，IMF）之和，并通过希尔伯特变换得到分量信号的瞬时频率和瞬时幅值[1].除EMD方法外，一些新的自适应时频分析方法被提出与研究，如LCD方法.LCD法自适应地将一个复杂信号分解为若干个相互独立的内禀尺度分量（Intrinsic Scale Component，ISC）之和[2].实际上，EMD与LCD的分解思路是相同的，都首先采用基于极值点的局部特征尺度参数定义一种瞬时频率具有物理意义的单分量信号，然后据此进行自适应分解，其中EMD定义了IMF分量，LCD定义了ISC分量.因此，EMD和LCD都存在一些共同的缺陷，如模态混淆、分解过程的伪分量问题等[3-4].另外，单分量信号IMF和ISC的定义缺乏严格的数学证明.

受压缩感知理论以及EMD方法的启发，Hou和Shi于2011年提出了一种自适应最稀疏时频分析（ASTFA）方法[5-6]，主要思想是基于多尺度数据具有内在的稀疏时频分布的特点，采用高斯牛顿迭代法解决非线性优化问题实现信号的分解.ASTFA方法以分解得到的单分量个数最少为优化目标，以单分量的瞬时频率具有物理意义为约束条件，在目标优化的过程中实现信号的自适应分解，并直接得到各个分量的瞬时频率和瞬时幅值，从而获得原始信号完整的时频分布.ASTFA方法与EMD及LCD方法不同，其具有严格的数学基础[7]，每个分量信号都具有明确的物理意义.

实际上，自适应时频分析方法并不是对所有的多分量信号都能实现有效分解，分解能力存在一定的局限性.文献[8-9]对EMD方法的分解能力做了研究，研究表明EMD的分解能力与分量信号的频率比及振幅比有关，当分量的频率太过接近或者高、低频分量的幅值比太小时，EMD方法不能实现分量的有效分离.类似于EMD方法的分解能力研究，文献[10]通过建立分解能力研究模型研究了频率比、幅值比及初始相位差对LCD分解能力的影响，研究表明初始相位差的影响很小，频率比及幅值比的影响明显.以上研究表明，以双谐波分量合成信号的分解效果来评估自适应时频分析方法的分解能力是一种非常有效的方法.本文基于双谐波分量合成信号的分解来研究频率比、幅值比、初始相位差对ASTFA方法分解能力的影响，并与EMD及LCD方法进行对比.结果表明，ASTFA方法的分解能力具有一定的优越性.

1ASTFA方法

ASTFA方法基于多尺度数据具有内在稀疏分布的特点，在建立包含所有内禀模态函数的过完备字典库的基础上寻找信号的最稀疏表达.ASTFA方法首先建立合适的过完备字典库，然后在过完备字典库中搜索对数据的匹配性最好的自适应基.

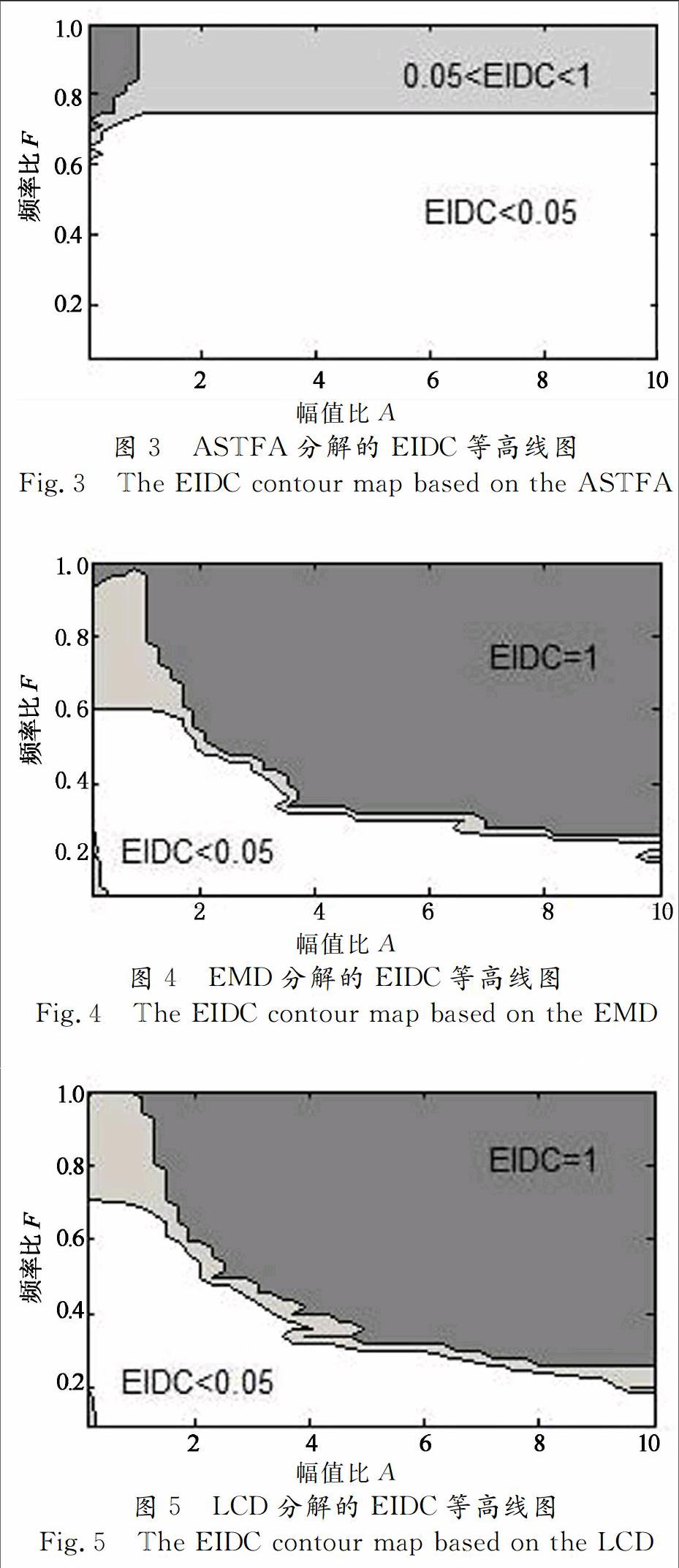
1）ASTFA方法的完全分解区明显大于EMD和LCD方法的完全分解区，表明ASTFA方法的分解能力明显强于EMD和LCD方法.且ASTFA方法能够分解的最大频率比为F=0.74，EMD方法能够分解的最大频率比为F=0.61，LCD方法能够分解的最大频率比为F=0.69.

2）ASTFA方法的完全不分解区明显小于EMD和LCD方法的完全不分解区，同样表明ASTFA方法的分解能力明显强于EMD和LCD方法.

3）ASTFA方法的分解能力基本不受幅值比的影响，但是在频率比0.61

4）EMD和LCD方法的区域划分非常相似，同时在低频率比、低幅值比情况下有分量无法完全分离的情况.这种相似性现象的出现是由于EMD和LCD采用了相同的分解思路.

为验证图3—图5计算结果的正确性，考察式（10）所示的仿真信号x（t），t∈[0，1]，设定幅值比A=1.频率比F与EIDC的关系如图6所示，由图6可知，在式（10）的分析模型下，EMD能够分解的频率比上限为F=0.61，LCD能够分解的频率比上限为F=0.67，ASTFA能够分解的频率比上限为F=0.74，结果表明了计算的正确性.

为验证图3—图5计算结果的正确性，考察式（11）所示的仿真信号，设定频率比为F=0.4.幅值比A与EIDC的关系如图7所示，由图7可知，在式（11）的分析模型下，EMD能够分解的幅值比上限为A=3.85，LCD能够分解的幅值比上限为A=3.35，ASTFA的 EIDC值基本接近于0，结果不但表明了计算的正确性，而且表明ASTFA有良好的分解精度.

从图9中可以看出，ASTFA准确地将两个分量信号进行分离.结果证明ASTFA方法除在频率比0.61

2.3初相位差φ对分解能力的影响

前面在研究频率比F，幅值比A对分解能力的影响时，设定初相位差φ=0.现在进一步研究初相位差φ对ASTFA方法分解能力的影响，初始相位差φ∈[-2π，2π].为研究初相位差φ对ASTFA方法分解能力的影响，考察式（13）所示的仿真信号，频率比F=0.4，幅值比A=1，位于完全可分解区域.仿真信号的初相位差φ与EIDC的关系如图10所示.从图10中可以看出，EIDC值变化不大，初始相位差对分解能力基本无影响.

为更具一般性，在不完全可分解区域选择一个合成信号，频率比F=0.8，幅值比A=3，具体如式（14）.仿真信号的初相位差φ与EIDC的关系如图11所示.从图11中可以看出，EIDC值变化不大，初始相位差对分解能力基本无影响.综合图10和图11可以知道，对于不同的频率比F和幅值比A，初始相位差φ对ASTFA方法的分解能力基本无影响.

3结论

根据本文的研究，可以得到以下结论：

1）频率比对ASTFA方法的影响较大，ASTFA方法可分解的极限频率比为0.74，该极限频率比优于EMD和LCD方法.

2）幅值比对ASTFA方法的影响较小，除去频率比0.61

3）初始相位差对ASTFA方法的分解能力基本无影响.

通过本文的研究发现，与EMD和LCD方法相比，ASTFA方法的分解能力具有明显的优越性，ASTFA方法将会得到广泛的关注.但是ASTFA方法中相位初始值的选择非常关键，需在后续的应用中对相位初始值的选择进行深入的研究.

参考文献

[1]HUANG N E，SHEN Z，LONG S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A，1998，454：903-995.

[2]杨宇，曾鸣，程军圣.一种新的时频分析方法—局部特征尺度分解[J].湖南大学学报：自然科学版，2012，39（6）： 35-39.

YANG Yu，ZENG Ming，CHENG Jun-sheng.A new time-frequency analysis method—the local characteristic-scale decomposition[J].Journal of Hunan University： Natural Sciences，2012，39（6）：35-39.（In Chinese）

[3]汤宝平，董绍江，马靖华.基于独立分量分析的EMD模态混叠消除方法研究[J].仪器仪表学报，2012，33（7）：1477-1482.

TANG Bao-ping，DONG Shao-jiang，MA Jing-hua.Study on the method for eliminating mode mixing of empirical mode decomposition based on independent component analysis [J].Chinese Journal of Scientific Instrument，2012，33（7）：1477-1482.（In Chinese）

[4]郑近德，程军圣，杨宇.部分集成局部特征尺度分解：一种新的基于噪声辅助数据分析方法 [J].电子学报，2013，41（5）：1030-1035.

ZHENG Jing-de，CHENG Jun-sheng，YANG Yu.Partly ensemble local characteristic-scale decomposition： a new noise assisted data analysis method [J].Acta Electronica Sinica，2013，41（5）：1030-1035.（In Chinese）

[5]HOU T Y，SHI Z Q.Adaptive data analysis via sparse time-frequency representation[J].Advances in Adaptive Data Analysis，2011，3（1/2）：1-28.

[6]HOU T Y，SHI Z Q.Data-driven time-frequency analysis [J].Applied and Computational Harmonic Analysis，2013，35（2）：284-308.

[7]HOU T Y，SHI Z Q，TAVALLALI P.Convergence of a data-driven time-frequency analysis method [J].Applied and Computational Harmonic Analysis，2014，37（2）：235-270.

[8]RILLING G，FLANDRIN P.One or two frequencies？ The empirical mode decomposition answers[J].IEEE Transactions on Signal Processing，2008，56（1）：85-95.

[9]FELDMAN M.Analytical basics of the EMD： two harmonics decomposition [J].Mechanical Systems and Signal Processing，2009，23（7）：2059-2071.

[10]杨宇，曾鸣，程军圣.局部特征尺度分解方法及其分解能力研究[J].振动工程学报，2012，25（5）：602-609.

YANG Yu，ZENG Ming，CHENG Jun-sheng.Research on local characteristic-scale decomposition and its capacities [J].Journal of Vibration Engineering，2012，25（5）：602-609.（In Chinese）