刍议椭圆离心率范围的通性解法
2016-06-01 11:29:54陆修群
数学学习与研究 2016年24期
◎陆修群
(江苏省如东县丰利中学,江苏 如东 226408)
刍议椭圆离心率范围的通性解法
◎陆修群
(江苏省如东县丰利中学,江苏 如东 226408)
椭圆离心率范围问题在近几年的高考或者各地的模拟考试中经常出现,对离心率范围的考查要求较高,有一定的难度,但其解法也有着一般性的规律,下面根据本人的教学实践就离心率范围的解法规律进行一些总结.
离心率;通性解法
通性解法一:根据线段、三角等不等关系构造a,b,c的不等式求离心率的范围.
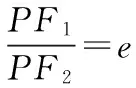
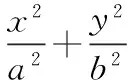
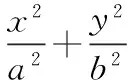
因为圆M与y轴相交于P,Q两点,所以M到PQ的距离就是M点横坐标的绝对值c,
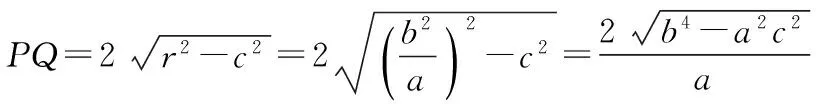
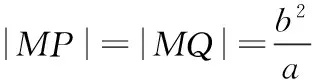
所以∠PMQ为钝角,
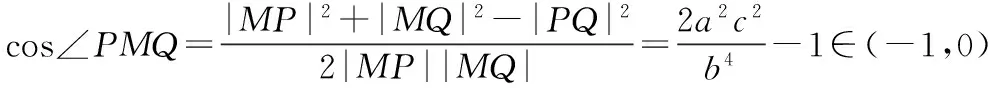
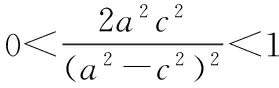
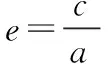
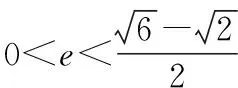
通性解法二:根据已知条件探究椭圆上点的横坐标x0或者角度等的范围求离心率的范围.
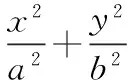
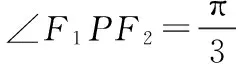
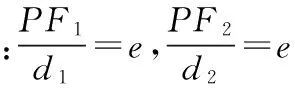
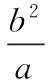
从2016年各省对离心率范围问题的考查可以发现,借助于线段、角度等的范围来构造a,b,c的不等式进而求解离心率的范围比较方便,但是线段、角度等的范围研究就需要学生对问题加强深入探究,做好问题的合理、科学的转化.
猜你喜欢
高中数理化(2024年1期)2024-03-02 17:52:40
阅读(快乐英语中年级)(2022年10期)2022-11-08 06:30:48
阅读(快乐英语高年级)(2022年9期)2022-10-08 08:06:14
当代水产(2021年11期)2022-01-15 05:38:34
当代水产(2021年2期)2021-03-29 02:57:24
中学数学杂志(2019年1期)2019-04-03 00:35:42
广东教育·高中(2017年10期)2017-11-07 10:14:24
小布老虎(2017年2期)2017-07-31 17:14:34
江苏蚕业(2015年2期)2015-02-05 22:26:12
新高考·高二数学(2014年7期)2014-09-18 00:44:12

