小学数学中的辩证唯物主义观点

◎徐燕萍

(江西省上饶市余干县实验小学，江西 上饶 334000)

小学数学中的辩证唯物主义观点

◎徐燕萍

(江西省上饶市余干县实验小学，江西 上饶 334000)

小学数学课堂教学要突出思想性.辩证唯物主义的哲学思想是数学教学与研究的指导思想之一，小学数学教学内容中蕴含着哲学思想.在小学数学中的辩证唯物主义主要表现在“相互联系”“抓住主要矛盾”“对立统一”“发展变化”等方面，需在教学实践中积极地挖掘，并逐步渗透到学生的学习当中去.

小学数学；辩证法；辩证唯物主义

不仅是小学语文课堂教学，小学数学课堂教学也要突出思想性，在对学生进行思想品德教育的时候，关于辩证唯物主义观点的渗透是比较薄弱的方面.其实，小学数学教学内容中蕴含着丰富的辩证唯物主义的思想观点.根据我的经验与分析，辩证观点在小学数学中主要表现在“相互联系”“抓住主要矛盾”“对立统一”“具体问题具体分析”“发展与变化”等方面，这需要我们老师在教学实践中积极地挖掘，并逐步渗透到学生的学习当中去.

一、“相互联系”的观点在有余数除法的释疑中渗透

多数教师在讲有余数的除法时，除法算式的得数采用的是将余数附在商的后面，用省略号连接的方式，比如“45÷6=7……3”“11÷2=5……1”.省略号非数学运算符号，所以上述式子并非严格意义上的等式.但在小学低年级的教学中采取这种形式也是无奈之举，由于学生的认知局限，只为方便学生的理解.直到学生升入高年级时，上述表达的等式的负面影响逐渐显露出来，爱思考的学生会发现并提出一种令人难以解释的现象：如，10÷3=3……1、7÷2=3……1.这两式子的右边明明一样，所以有学生想当然地认为式子的左边也应该是相等的，于是推导得出10÷3=7÷2，很显然我们能看出两式子是不相等的.学生会被自己的这种发现搞糊涂了，老师须解惑释疑.

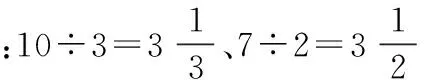
二、“抓住主要矛盾”的观点在小数大小比较的教学中渗透

比较小数大小的方法是：先比较其整数部分，整数部分大的小数较大；如果整数部分相等，就再比较小数部分的十分位，十分位的数较大的小数较大……从整数部分到小数部分，从高位到低位，不但体现了数学中的“井然有序”，而且暗喻着哲学中的“抓住主要矛盾”的观点——在问题的诸多矛盾中，必有一个矛盾是主要的，抓住这个主要矛盾，问题就能逐步得到解决.如，学生在比较10.098与10.102的大小时，由于按往常习惯8、9比1、2数字大，学生对于8、9数字“大”的印象太深刻，导致他们会先入为主地认为10.098比10.102大.实际上，在对小数10.098与10.102比较大小时，根本还轮不到“8、9”登场，它们处在次要数位上，可暂不考虑，而要抓主要矛盾，比较它们十分位上的0与1.很明显，10.102比10.098大.在平时的训练中，老师也会经常出一些如上的习题，以干扰学生的注意力，让他们判断.如果学生懂得运用“抓住主要矛盾”的观点，再复杂奇异的小数大小比较都能被“秒杀”完成.

三、“对立统一”的观点在分数除法的教学中渗透

四、在小数末尾的0的去留上渗透“发展变化”的观点

老师教学小数知识后，学生大都知道，凡是小数末尾的0，都可以去掉，因为去掉后小数的大小并不会改变.于是，老师会有意识地规定学生在做习题时要把小数末尾的0去掉.倘若有人在计算得数时没去掉小数末尾的0，将会受到批评，试卷出现此情况，可能将被评为错误的解答.久而久之，学生就养成了将小数末尾的0去掉的习惯.然而，事情往往有利亦有弊，此习惯的养成，对于近似数知识的学习又会带来负面的影响.比如，作为近似数1.680与1.68是不相同的：1.680精确到0.001，而1.68只精确到0.01.如果学生根据以往习惯将1.680“化简”成1.68，就要犯错了.因此老师要尽量防止这种由旧知所带来的干扰.对于近似数末尾的0不能随便去掉，在教学的开始，学生或许会感到不适应，甚至还会有人埋怨这种要求上的“变动”：老师彼时那样规定，此时又这样说，把我们都搞糊涂了，到底小数末尾的0是否要去掉呢.这时，老师就应该及时向学生说明情况：世界上的万事万物都处于不断变化、发展之中的，任何事物都不可能一成不变.既然万事万物皆在变动，我们静止地、停滞地看问题就很可能导致失误，应当不断地学习与思考，努力使自己的思维与思想适应永恒变化的情况.

数学与哲学是紧密联系的学科，历史上的许多数学家又是哲学家，正说明这一点.在小学阶段，学生的思维能力还在启蒙时期，初始的训练至关重要，老师要善于引导并启发学生的数学思维，抓住每一次课堂教学对辩证观点的渗透时机，使他们明白辩证观点在数学学习中的重要性与必然性，并努力内化辩证唯物主义思想为自己所用.

[1]许梅红.谈数学教学中“辩证唯物主义观点”的教育[J].时代教育(教育教学版),2008(08).