利用Matlab优化多元函数微积分教学的研究与实践

吴兴杰，解大鹏，刘　洋，许和乾

(合肥师范学院 数学与统计学院，安徽 合肥 230601)



利用Matlab优化多元函数微积分教学的研究与实践

吴兴杰，解大鹏，刘洋，许和乾

(合肥师范学院 数学与统计学院，安徽 合肥 230601)

[摘要]在多元函数微积分教学中融入Matlab数学软件，可为抽象的数学思维提供直观模型，几个相关的教学实例表明，这不但有利于提高学生分析和解决问题的能力，激发学生的学习积极性和创造性，而且能有效的提高多元函数微积分的教学质量和效率。

[关键词]Matlab；多元函数微积分；探究式教学

1引言

高等数学作为大学理工科各专业的一门非常重要的基础课，是学生学好其它基础课和专业课程的基础，它为学生学习后续课程和解决实际问题提供了必不可少的知识，此外，高等数学还是理工科学生攻读研究生所必须参加的一门考试课[1]。然而，由于该课程十分抽象，尤其是有关多元函数微积分的教学，传统的教学方式往往缺乏生动性和直观性，很难做到教学互动，学生学习普遍感到非常困难，教学效率低，不利于人才的培养，这些都反映出高等数学教学改革的迫切性[2]，因此，如何提高高等数学的教学效果以及怎样将数学知识与专业背景进行有机结合，就成为亟待解决的问题[3]。

多媒体现代技术在高校中的普及，也越来越使得教学工作更加简洁便利，其对培养学生的数学探究创新和数学实践能力有着不可替代的重要作[4，5]。近年来，国外很多知名高校都将数学软件引入到高等数学教学中，Matlab具有典型的图形可视化功能，在进行多元函数的性质、曲面和空间立体图形的关系、偏导数与连续的关系、多元函数的极值、重积分的几何意义以及多元函数微积分在几何和物理上的应用等方面的教学中[6-8]，适当利用Matlab软件进行数学实验，应用数值表格或直观图像来分析复杂的数学问题，通过先直观、后抽象，先观察、归纳、总结，后演绎推理、分析证明，把知识的传授过程变成更符合认知规律的以引导学生主动学习的探究知识的过程，这能很好弥补传统教学的不足，提高教学效率，激发学生主动学习的积极性，进而提高学生应用高等数学知识解决实际问题的能力[6，9]。

2偏导数、全微分的几何意义与应用

设二元函数z=f(x,y)在点(x0,y0)处具有偏导数(这里仅以对x的偏导数为例)，过曲面z=f(x,y)上一点M0(x0,y0,f(x0,y0))作平面y=y0，截此曲面于曲线z=f(x,y0)，由于偏导数fx(x0,y0)为一元函数f(x,y0)的导数f′(x,y0)|x=x0，故由一元函数的几何意义可知，fx(x0,y0)表示曲线z=f(x,y0)在M0处切线对x轴的斜率，即z=f(x,y)在(x0,y0)处沿平行于x轴的变化率。

例1讨论函数z=2-2x2-y2在(0.5,0.5)处对x的偏导数的几何意义。

分析二元函数表示的曲面、曲面被平面y=0.5所截的平面曲线z=1.75-2x2以及曲线在x=0.5处的切线z=2.25-2x如图1。

然而，偏导数的存在只能保证点(x,y)沿平行于x和y轴的特殊方式趋于(x0,y0)时，函数值f(x,y)趋于f(x0,y0)，或者说在(x0,y0)处沿x和y轴方向是连续的，但不能保证点(x,y)沿任何路径趋于(x0,y0)时，f(x,y)均趋于f(x0,y0)，因此对多元函数来说，即使各偏导数存在也不能保证函数连续。

例2[1]讨论二元函数

在(0，0)处的连续性。

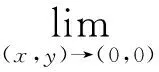
在一元函数中，可微函数的几何意义是：可以用切线段近似代替弧段。对于二元函数来说，其全微分也有类似的意义。

设二元函数z=f(x,y)在(x0,y0)处可微，则在点(x0,y0)的某邻域内有f(x,y)-f(x0,y0)≈fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0)，即f(x,y)≈f(x0,y0)

+fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0)，记上式左端为z=f(x0,y0)+fx(x0,y0)(x-x0)

+fy(x0,y0)(y-y0)，其表示过P0(x0,y0,f(x0,y0))，曲面z=f(x,y)的切平面，因此曲面在P0近旁的小部分可用切平面代替，即以平面代替曲面，这样全微分df|(x0,y0)就表示曲面z=f(x,y)在点P0处切平面上点的竖坐标的增量。

例3讨论二元函数z=20-x2-y2在(-0.5,-0.5)处的全微分。

分析zx|(-0.5-0.5)=zy|(-0.5,-0.5)=1，这样dz|(-0.5,-0.5)=dx+dy。在区域[-1,0]×[-1,0]内曲面及其在点(-0.5,-0.5)处的切平面如图3。

3多元函数极值点的应用分析

多元函数极值的定义及其数学意义成为高等数学教学中的一个难点内容。通过Matlab的绘图功能，能将多元函数极值求解的基本思路和方法实现图形化表示，更清楚地揭示多元函数极值的数学意义，从而促进学生对多元函数极值问题的理解和掌握。

定义1[1]若函数z=f(x,y)在点(x0,y0)的某邻域内有定义，且对该邻域内的所有点(x,y)有f(x,y)⦤f(x0,y0)或f(x,y)≥f(x0,y0)，则称函数在(x0,y0)处取得极大值或极小值。

从定义上说，对二元函数在(x0,y0)处取得极值，学生不十分清楚是什么样的情形，尤其对在(x0,y0)处不取极值，虽然可文字解释为不存在(x0,y0)的邻域使得定义1中的不等式成立，或说(x0,y0)的任何邻域中即有使得f(x,y)⦤f(x0,y0)的点，又有使得f(x,y)≥f(x0,y0)的点，但学生还是渴望能更直观地展示这一含义。

例4[1]讨论函数f(x,y)=x3-y3+3x2+2y2-9x的极值。

分析易求f(x,y)的四个驻点(1,0),(1,2),(-3,0),(-3,2)。虽然可利用极值的充分条件[1](大部分高等数学教材不予证明)来判断f(x,y)在(1,0)处取得极小值，在(-3,2)处取得极大值，在(1,2),(-3,0)处均不取极值，但是大部分学生对这些结果产生疑惑，极大值、极小值在曲面上表现如何？在(1,2),(-3,0)处不取极值的直观图形是什么？下面通过Matlab将结果可视化，更直观、更深刻地解释多元函数的极值问题。利用Matlab作出f(x,y)的三维曲面(如图4)和等高线(如图5)。

从图5可清楚地看出，函数f(x,y)具有两个极值点，根据梯度与等高线的关系，梯度的方向是等高线的法线方向且指向函数增长的方向，由此可知，极值点应该有等高线环绕，图5显示，这里的极值点包括极大值点(-3,2)和极小值点(1,0)。由图5可见，点(1,2),(-3,0)的周围没有等高线环绕，故不是极值点，在图4表现为鞍点，这就解释了定义中(x0,y0)的任何邻域中即有使得f(x,y)⦤f(x0,y0)的点，又有使得f(x,y)≥f(x0,y0)的点了，这些与利用极值的充分条件分析的结果一致。

4重积分的计算分析

例5[1]求球体x2+y2+z2⦤4a2被圆柱面x2+y2=2ax, (a>0)所截得的立体体积。

分析这其实就是著名的维维安尼(Viviani)体，通过Matlab展现出截得的立体图形，如图6(这里以a=2为例)。

由所求立体的对称性，这里仅求第一卦限内的部分体积后乘以4即得所求立体的体积。第一卦限内的立体是一个曲顶柱体，如图7。

三重积分的计算是高等数学的一个教学难点，要求学生具有较强的几何直观能力。利用Matlab将积分区域清晰地展现出来，不仅使重积分的计算简洁、准确，而且可增强学生的空间想象和应用数学去解决实际问题的能力，提高教学效果。

分析首先，利用Matlab作出积分区域V及其在xoy面上的投影区域Dx,y如图8。

图8显示积分区域中曲面z=18-0.5(x2+y2)在曲面z=5+x2+y2上方，两曲面方程联立可得其交线为x2+y2=9, (z=14)，其在xoy平面上的投影为以原点为心，半径为3的圆，此圆围成的区域(即V在xoy平面上的投影区域Dx,y)为x2+y2⦤9，根据柱面坐标变换可得所求三重积分

5结束语

总之，Matlab在高等数学尤其是在具有代表性的多元函数微积分的教学中起着重要的辅助作用，利用Matlab数学软件，结合多媒体技术，对多元函数微积分进行辅助教学，不仅丰富了教学资源，充分调动了学生的学习积极性和创造性，促进信息技术与数学教学的整合，而且对传统教学起到有益的补充作用，对进一步提高教学质量和效果具有实践性和重要的实际意义。

[参考文献]

[1]同济大学数学系. 高等数学第六版下册[M]. 高等教育出版社, 2007.

[2]荆科, 康宁. 提高高等数学教学效果的若干实践[J]. 新乡学院学报, 2014, 31(4): 66-69.

[3]许和乾, 杜炜. 基于数学软件Mathematic的高等数学教学实践[J]. 合肥师范学院学报, 2014, 32(3): 76-78.

[4]李秦. 计算机辅助高等数学教学的研究及实践[J]. 数学教学研究, 2013, 32(10): 60-64.

[5]声惠萍. 信息技术下运用MATLAB优化数学教学[J]. 信息技术, 2012, 9: 228-229.

[6]王彪. Matlab在高等数学教学中的应用[J]. 计算机与数字工程, 2013, 8: 1357-1359.

[7]仇海全, 潘花. Matlab在重积分计算中的应用[J]. 重庆工商大学学报(自然科学版), 2012, 29(4): 50-54.

[8]陈定元, 王业庆. 多元函数教学中应注意的几个问题[J]. 安庆师范学院学报(自然科学版), 2005, 11(2): 79-81.

[9]王红勇, 廖茂新, 杨德牛. 高等数学“探究式教学”浅谈-以二重积分换元法为例[J]. 教学研究, 2015, 28(1): 152-153.

Research and Practice of Multiple-variable Calculus Teaching Based on Matlab Software

WU Xingjie, XIE Dapeng, LIU Yang， XU Heqian

(SchoolofMathematicsandStatistics,HefeiNormalUniversity,Hefei230601,China)

Abstract：Matlab software can be used in the teaching of multiple-variable calculus, providing intuitive model for abstracted mathematical thinking. Several related teaching examples show that this approach will be not only helpful to improve students' ability to analyze and solve problems and stimulate the students' enthusiasm, but improve the quality and efficiency of multiple-variable calculus teaching as well.

Key words：Matlab; Multiple-variable calculus; Inquiry teaching

[收稿日期]2015-09-02

[基金项目]安徽省高等学校省级质量工程项目(2013jyxm173)；合肥师范学院重点教学研究项目(2012yj04)；合肥师范学院自然科学青年基金(2015QN18)；安徽省高等学校自然科学研究重点项目(KJ2015A196)；合肥师范学院“136人才项目工程”

[第一作者简介]吴兴杰(1981-)，男，安徽太和县人，博士，讲师，研究方向：微分动力系统，网络化智能体控制。

[中图分类号]G642.0

[文献标识码]B

[文章编号]1674-2273(2016)03-0059-04