基于加权非负矩阵分解的非负张量分解算法

刘路路,刘亚楠，王　凡

(合肥师范学院 计算机科学与技术系，安徽 合肥 230601)



基于加权非负矩阵分解的非负张量分解算法

刘路路,刘亚楠，王凡

(合肥师范学院 计算机科学与技术系，安徽 合肥 230601)

[摘要]提出一种基于加权非负矩阵分解的非负张量分解算法。为了充分利用图像本身的结构信息与内在几何结构，首先根据图像类别构造权值矩阵，把图像集合构造成三阶张量，然后，针对该三阶张量利用张量几何运算与非负矩阵分解得到非负张量分解算法的初值，最后实现图像的分类。实验结果表明该算法应用于手写数字图像库中能有效改善图像分类的准确性。

[关键词]图像分类；非负矩阵分解；非负张量分解

1引言

非负矩阵分解(NMF)[1]被广泛应用于图像处理、计算机视觉、数据挖掘等领域中[2] [3]，它使分解后的所有分量均为非负值，并且同时实现非线性的维数约减。然而在很多情况下，需要处理的数据是高于二维即为多维(张量)数据，如果在图像处理领域中采用NMF方法，需要把图像数据拉直成向量形式，在转换过程中会丢失图像数据本身的结构信息，破坏图像的空间几何结构，为了避免这些问题，Welling等人[4]把NMF推广到非负张量分解(NTF)，NTF被应用广泛于图像处理与模式识别领域[5] [6]。

本文提出一种基于加权NMF的NTF的算法，将张量空间的结构模拟成一个近邻图，根据图像的类别构造权值矩阵，并将图像集合构造成三阶张量，利用张量几何运算和NMF算法得到NTF的初值，最后利用迭代算法求解NTF，并将其应用于手写数字数据库分类中。

2背景介绍

2.1张量几何相关运算

本文算法中用到的张量几何[7]的相关定义和定理如下：

定义1(张量矩阵展开)是将一个张量中的元素重新排列，得到一个矩阵的过程，张量X∈RI1×I2×…×IN的n模展开矩阵表示为X(n)∈RIn×(I1...In-1In+1...IN)。

定义2(张量乘法)张量与矩阵的乘法由n模乘积所定义。具体地，张量X∈RI1×I2×…×IN和矩阵U∈RJn×In的n模乘积表示为X×nU，这是一个I1×I2×...×In-1×Jn×In+1×...×IN阶张量，定义如下：

(1)

2.2NMF

定义1NMF是发现非负的m×r的基矩阵W和r×n的系数矩阵H使[1]

V≈WH

(2)

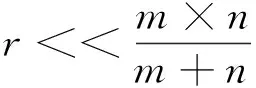
2.3NTF

现有的张量分解模型一般分为两类：标准分解模型[8]和Tucker分解模型[9]。这两种分解模型都是对矩阵奇异值分解的高阶推广，并且第一种分解模型是第二种分解模型的特例。非负Tucker模型(NTF)的目标是把非负张量X∈RI1×I2×…×IN分解为

(3)

其中：G∈RJ1×J2×…×JN，Un∈RIn×Jn(Jn⦤In，n=1,2,…N)。该分解可通过求解最优化问题式(4)得到：

(4)

3基于NMF的NTF算法

由(4)构造目标函数：

(5)

对(5)求偏导可得：

(6)

(7)

(8)

(9)

其中，G(n)为对应张量G的n模展开矩阵。

由公式(6)可得G的迭代规则：

(10)

由公式(7)可得U1的迭代规则：

(11)

由公式(8)可得U2的迭代规则：

(12)

由公式(9)可得U3的迭代规则：

(13)

由 (10)-(13)可知，迭代求解G、U(n)必须首先已知G、U(n)的初值，传统的方法是随机给G、U(n)赋初值，这样直接影响到图像最终的分类性能。为了避免这种随机性对分类性能的影响，本文构建近邻图G=(V,E)模拟数据集合X={X1,X2,...,XN}∈RI1×I2×N(Xn∈RI1×I2,n=1,2,...,N)的几何结构，定义G的权重矩阵W如下：

(14)

本文利用该W与张量数据集合X做加权NMF，以得到U(n)(n=1,2,3)的初值。具体算法思路见算法1。

算法1加权NMF

(1) 针对数据集合X，X∈RI1×I2×N构造3阶张量

(2) 求得X∈RI1×I2×N与W∈RN×N的3模乘积X×3W，记为A，A∈RI1×I2×N

(3) 对A进行n模展开，得到A(n)，(n=1,2,3)

(4) 对A(n)分别进行NMF分解得到U(n)，(n=1,2,3)

随后，利用U(n)的值根据公式(10)得到G的初值。

(15)

最后，由(11)、(12)可以得到U1、U2，由U1、U2可得Xi对应子空间中的Yi，(i=1,2,...,N)：

(16)

4实验结果

为了验证本文算法的有效性，采用手写数字数据库USPS Handwritten Digits和Binary Alphadigits[10]。

第一个数据库包含0～9等十个数字共10类，每类有1100幅图像，图像为20×20的灰度图像，从中随机选取400幅图像做两组实验。第一组实验是随机选取100幅图像做训练，其余图像做测试；第二组实验是从每类中随机选取200幅图像做训练，其余图像做测试。第二个数据库包含0～9等十个数字，以及“A”～“Z”等26个英文字母，共36类，每类有39幅图像，图像为20×16的灰度图像。对该数据库同样做两组实验，第一组实验是从每类中随机选取10幅图像做训练，其余图像做测试；第二组实验是从每类中随机选取20幅图像做训练，其余图像做测试。

本文选用PCA[11]、2D-PCA[12]、NTF与本文提出的基于NMF的NTF方法做对比，每一种方法均采用最近邻分类器进行分类。对本文方法、NTF来说，两幅图像之间的距离：

‖U1TXiU2-U1TXjU2‖

(17)

对PCA、2D-PCA来说，两幅图像之间的距离是主成分子空间的欧几里德距离。分类结果如图1、2所示，横轴为维数，纵轴为分类准确度。从图中可以看出本文算法优于其他三种对比算法，并且NTF算法明显优于2D-PCA、PCA。

5总结

为了保持图像数据空间的几何结构，鉴于非负张量分解的优势，本文提出一种基于高阶非负矩阵分解的非负张量分解算法，对数据进行维数约减，并应用于手写体数据库中，实验结果表明本文算法可以有效提高分类准确率。后续将继续研究谱图理论在张量空间中的应用。

[参考文献]

[1]Lee D D, Seung H S. learning the parts of objects by non-negative matrix factorization [J]. Nature, 1999, 401(6755):788-791.

[2]Deng Cai, Xiaofei He and Jiawei Han. Graph Regularized Non-negative Matrix Factorization for Data Representation[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2011,33(8):1548-1560.

[3]Mohamed Ouhsain A. Ben Hamza. Image watermarking scheme using nonnegative matrix factorization and wavelet transform [J]. Expert Systems with Applications. 2009, 36(2): 2123-2129.

[4]Welling M, Weber M. Positive tensor factorization [J]. Pattern Recognition Letters, 2001, Vol.22 (12):1255-1261.

[5]Ji Liu, Jun Liu, Peter Wonka , Jieping Ye. Sparse non-negative tensor factorization using columnwise coordinate descent [J]. Pattern Recognition, 2012,45(1): 649-656.

[6]Fengyu Cong, Anh Huy Phan, Piia Astikainen. Multi-domain Feature of Event-Related Potential Extracted by Nonnegative Tensor Factorization: 5 vs. 14 Electrodes EEG Data [J]. Lecture Notes in Computer Science, 2012, 7(9): 502-510.

[7]Lathauwer LD. Signal processing based on multilinear algebra [D], [Ph.D Thesis], Belgium: Katholieke Universiteit Leuven, 1997.

[8]R.A.Harshman. Foundations of the PARAFAC procedure: models and conditions for an "explanatory" mul-modal factor analysis [J]. UCLA working papers in phonetics, 1970, Vol.(16):1-84.

[9]L.R.Tueker. Some mathematical notes of three-mode factor analysis [J]. Psychometrika, 1966, 31 (3):279-311.

[10][Online]http://www.cs.nyu.edu/～roweis/data.html.

[11]Hotelling H. Analysis of a complex of statistical variables into principal components[J]. Journal of Educational Psychology, 1933, 24(6):417-441.

[12]Jian Y, David Z, Frangi A F, et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition.[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(1):131-7.

Non-negative Tensor Factorization Based on Weighted Non-negative Matrix Factorization

LIU Lulu, LIU Yanan, WANG fan

(SchoolofComputerScienceandTechnology,HefeiNormalUniversity,Hefei230039,China)

Abstract：This paper proposes a non-negative tensor factorization based on weighted non-negative matrix factorization. In order to fully use the structural information of the data and their intrinsic geometry, the weighted matrix is constructed according to the label of images and the set of images is constructed to a third order tensor first. Then using tensor geometry operation and non-negative matrix factorization can get the original values. Finally, image classification is realized. Experimental results on the handwritten digital image database show that the proposed algorithm can effectively improve the accuracy of the image classification.

Key words：image classification; non-negative matrix factorization; non-negative tensor factorization

[收稿日期]2016-01-18

[基金项目]安徽省高校省级优秀青年人才基金重点项目 (2011SQRL129ZD)，合肥师范学院科研项目(2015QN15)

[第一作者简介]刘路路(1982-)女，硕士，合肥师范学院计算机科学与技术系教师。研究方向：图像处理。

[中图分类号]TP391.4

[文献标识码]A

[文章编号]1674-2273(2016)03-0024-04