基于可调腔量子电动力学系统中多比特纠缠态的制备

高　媛，杨　名，余龙宝

(1. 安徽大学 物理与材料科学学院，安徽 合肥 230039；2.合肥师范学院 电子信息工程学院，安徽 合肥 230601)



基于可调腔量子电动力学系统中多比特纠缠态的制备

高媛1，杨名1，余龙宝2

(1. 安徽大学 物理与材料科学学院，安徽 合肥 230039；2.合肥师范学院 电子信息工程学院，安徽 合肥 230601)

[摘要]量子纠缠态是量子信息处理和量子通信领域中的核心资源。在量子计算机的硬件研究中，超导系统具有较为突出的优势，本论文结合该系统最新的实验进展，提出了在可调腔量子电动力学系统中实现多比特量子纠缠态的制备方案，频率可调的超导腔与相位比特之间的耦合作用形成XY形式，通过调节腔场的频率依次与不同的比特一个接一个地共振作用，并控制合适的作用时间，将会便捷地实现纠缠态制备。基于该系统可控制强、相干性好、易扩展等优点，本方案在实验上具有一定的可行性和指导意义。

[关键词]量子电动力学；可调腔；超导系统；XY相互作用；量子纠缠态

1引言

在量子信息处理和量子模拟领域中，超导量子比特和腔组成的系统是一直被认为最具前景的物理体系之一。近年来，该系统在实验上取得了突破性进展，已经制备出两比特、三比特、四比特的处理器，成功实现了初步的量子算法和纠错码编码[1-4]。为了提高超导比特的相干时间，耶鲁大学和IBM等实验小组相继采取了一系列的改进措施，例如将超导比特放进三维的腔[5-6]中，改进集成电路的几何形状和材料[7-10]等，这些方案同时都采用减小了电介质耗散[11]工艺手段，将相干时间提高了近两个数量级。即使有了这些改进，但距离实现大规模量子运算还有很大的差距，从实验角度来看，设计一个可控制微波频率谱线的集成量子电路已是当务之急。近十年，rf SQUID相位量子比特[12]得到稳定发展和广泛应用，特别是在多比特与腔耦合的系统[3,13-15]中。然而，该系统中对单个比特的测量是破坏性的，也会导致系统中其他比特或腔[16-19]的量子态受到严重影响。最新的一项实验[20]研究表明，频率可调的腔量子电动力学(QED)系统对相位比特的分离测量是一个理想的选择，也是实验发展的趋势。通过调节腔的频率，该系统不仅能实现非破坏性测量，实验上的各种操作也更便捷快速。

本文中，我们基于频率可调的腔QED 系统提出制备多比特的量子纠缠态，包括GHZ态、W态和cluster态。超导共振腔发挥着辅助作用，被调节到不同频率与相应量子比特共振相互作用，通过控制合适的作用时间，从而实现各种类型的纠缠态。

2可调腔量子电动力学模型

在腔QED系统中，一个共振腔与多个超导量子比特通过电感线圈连接起来，系统的哈密顿量可以表示为Jaynes-Cummings(JC)模型[20]：

(1a)

(1b)

(1c)

(2)

(3)

经过合适的时间演化，量子态在两子系统之间以一定频率进行振荡

(4)

从上式(3)中可以看出ISWAP逻辑门可以用来实现其他任意的两比特量子逻辑门，如由ISWAP逻辑门可以构建出控制非门(CNOT门)

CNOT门是由2个ISWAP逻辑门以及一些单比特操作来实现。

因此ISWAP门可以用来实现任意逻辑运算和制备纠缠态，下面我们分析由ISWAP逻辑门来构建逻辑线路图实现几种典型的多比特纠缠态。

3多比特纠缠态的制备

我们可以运用ISWAP门制备多比特纠缠态，如W态，GHZ态和Cluster态等。

(1)实现N个比特W态的制备

演化过程可以表示为：

(5)

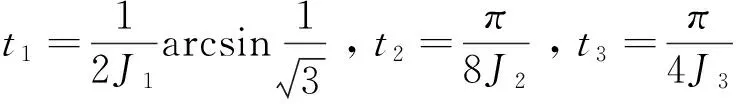
(2)N个比特GHZ态的制备过程

N个比特GHZ态的表达式为：

(6)

量子态演化过程可以表示为

(7)

(3)Cluster态的实现

一维Cluster态的表达式为：

(8)

(9)

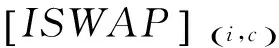
4讨论和总结

在量子纠缠态制备系统中超导腔和超导比特是当前实验组[20]所采用样品，实验温度在40mK下时腔的频率可调范围在6.2-8.7GHz，量子比特的频率由偏置电流调节在5-10GHz之间任意值，腔场的相干时间在1.8μs以上，每个量子比特的两个相干时间分别在T1=600ns和T2=310ns以上。为了避免比特之间不必要的耦合，可以使每个比特的频率间隔在200MHz以上，在实验操作中保持比特的频率为一个固定值，通过调节腔的频率依次与其进行共振相互作用，从而实现量子纠缠态制备的操作流程。每次调节腔场频率与比特形成耦合和失谐的过程仅需要2ns，共振作用的时间也在10ns左右，可以估计出制备十个比特的纠缠态不需要超过200ns的时间，也就是说，所有的操作时间都是在系统容许的相干时间内完成，能够得到保真度较高的目标态。

本文中我们利用了频率可调的腔QED 系统制备多比特的量子纠缠态，利用不同结构的操作流程实现了GHZ态、W态和cluster态等。在制备过程中超导共振腔发挥着辅助作用，被调节到不同频率与相应量子比特共振相互作用，通过控制合适的作用时间，可以得到高保真度的多比特量子纠缠态，利用现有的实验技术是可行的，与其他多粒子纠缠态制备相比较，操作过程有明显的简化，制备时间大大缩减，从而提高了实验效果和效率。

[参考文献]

[1]L. DiCarlo,etal., Demonstration of two-qubit algorithms with a superconducting quantum processor [J]. Nature (London) 2009, 460: 240-244.

[2]M. D. Reed,etal., Realization of three-qubit quantum error correction with superconducting circuits [J]. Nature (London) 2012, 482: 382-385.

[3]E. Lucero, et al., Computing prime factors with a Josephson phase qubit quantum processor [J]. Nat. Phys. 2012, 8: 719-723.

[4]M. H. Devoret and R. J. Schoelkopf. Superconducting Circuits for Quantum Information [J]. Science 2013, 339: 1169-1174.

[5]H. Paik,etal., Observation of High Coherence in Josephson Junction Qubits Measured in a Three-Dimensional Circuit QED Architecture [J]. Phys. Rev. Lett. 2011, 107: 240501.

[6]C. Rigetti,etal., Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms [J]. Phys. Rev. B 2012, 86: 100506.

[8]J.M. Chow,etal., Universal Quantum Gate Set Approaching Fault-Tolerant Thresholds with Superconducting Qubits [J]. Phys. Rev. Lett. 2012, 109: 060501.

[9]U. Patel,etal., Josephson phase qubit with a single crystal silicon capacitor [J]. Appl. Phys. Lett. 2013, 102: 012602.

[10]J. B. Chang,etal., Improved superconducting qubit coherence using titanium nitride [J]. Appl. Phys. Lett. 2013, 103: 012602.

[11]J. M. Martinis,etal., Decoherence in Josephson Qubits from Dielectric Loss [J]. Phys. Rev. Lett. 2005, 95: 210503.

[12]R.W. Simmonds,etal., Decoherence in Josephson Phase Qubits from Junction Resonators [J]. Phys. Rev. Lett. 2004, 93: 077003.

[13]M. A. Sillanpää, J. I. Park, and R. W. Simmonds, Coherent quantum state storage and transfer between two phase qubits via a resonant cavity [J]. Nature (London) 2007, 449: 438-442.

[14]R. McDermott,etal., Simultaneous State Measurement of Coupled Josephson Phase Qubits [J]. Science 2005, 307: 1299-1302.

[15]Chui-Ping Yang, Qi-Ping Su, and Jin-Ming Liu, Proposal for realizing a multiqubit tunable phase gate of one qubit simultaneously controlling n target qubits using cavity QED [J]. Phys. Rev. A 2012, 86: 024301.

[16]D. Risté, C. C. Bultink, K. W. Lehnert, and L. DiCarlo, Feedback Control of a Solid-State Qubit Using High-Fidelity Projective Measurement [J]. Phys. Rev. Lett. 2012, 109: 240502.

[17]P. Campagne-Ibarcq,etal., Feedback Control of a Solid-State Qubit Using High-Fidelity Projective Measurement [J]. Phys. Rev. X 2013, 3: 021008.

[18]L. Steffen,etal., Deterministic quantum teleportation with feed-forward in a solid state system [J]. Nature (London) 2013, 500: 319-322.

[19]A. A. Houck, et al., Controlling the Spontaneous Emission of a Superconducting Transmon Qubit [J]. Phys. Rev. Lett. 2008, 101: 080502.

[20]J. D. Whittaker,etal., Tunable-cavity QED with phase qubits [J]. Phys. Rev. B 2014, 90: 024513.

Generation of Multi-qubit Quantum Entanglment States in Tunable Circuit QED

GAO Yuan1, YANG Ming1, YU LongBao2

(1.SchoolofPhysicsandMaterialScience,AnhuiUniversity,Hefei230601,China;2.SchoolofElectronicandInformationEngineering,HefeiNormalUniversity,Hefei230601,China)

Abstract：Quantum entanglement is the central resource in the quantum information process and quantum communication. In the research of quantum computing hardware, superconducting circuit is one of the more prominent system. In the paper, based on the latest research, we propose a scheme to generate multi-qubit entanglement states in quantum electrodynamics (QED). The coupling interaction which occurs between the frequency-tunable cavity and superconducting qubits, is the XY model. The cavity can interact with the superconducting qubits one by one with appropriate times. The entanglement states can be achieved more quickly and conveniently. The system has many advantages, such as better controllability, coherence, scalability, so the scheme has a certain feasibility and is instructive for the experiments.

Key words：quantum electrodynamics; tunable cavity; superconducting system; XY interaction; quantum entanglement

[收稿日期]2016-02-25

[基金项目]合肥师范学院校级项目(2015JG03)；安徽大学研究生创新项目(yqh100014)

[第一作者简介]高媛(1988-)，女，安徽大学硕士研究生，主要研究方向：量子信息。

[中图分类号]O413.2

[文献标识码]A

[文章编号]1674-2273(2016)03-0012-04