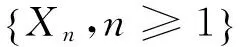END随机变量序列的完全收敛性

张永军

(合肥学院 学报编辑部, 安徽 合肥 230601)



END随机变量序列的完全收敛性

张永军

(合肥学院 学报编辑部, 安徽 合肥 230601)

[摘要]利用END随机变量的矩不等式, 研究END随机变量序列的完全收敛性, 所得结果推广了独立随机变量及若干相依变量的相应结果。

[关键词]END序列; 矩不等式; 完全收敛性

1预备知识

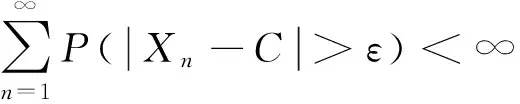
定义1对随机变量序列{Xn,n≥1}, 若存在常数M>0, 对于任意的n≥1和一切实数x1,x2,…,xn都有

(1)

(2)

同时成立, 则称{Xn,n≥1}为Extended Negatively Dependent(END)序列。

END序列的概念由文献[2]给出，当M=1，END序列即为NOD序列。而NOD随机变量的概念又比NA随机变量宽泛，文献[3-7]给出NOD随机变量序列的相关性质和极限定理。END序列是一类比NA序列及NOD序列更广泛的相依变量，研究其极限性质和应用具有较好的理论和实际意义。文献[2]获得了END重尾随机变量的精确大偏差, 文献[8]给出了END重尾随机变量偏差的充分必要条件, 文献[9]和[10]得到END随机阵列加权和的完全收敛性结果。

本文中, 设{Xn,n≥1}是定义在概率空间(Ω,F,P)上的END随机变量序列。 C是正常数, 在不同的地方可取不同的值。

引理 1[2]设随机变量X1,X2,…,Xn为END随机变量，若f1,f2,…,fn同为非降(或非增)函数,则f1(X1),f2(X2),…,fn(Xn)仍为END随机变量。

引理2[11]设{Xn,n≥1}是均值为零的END序列，则存在仅依赖于p的正常数Cp，使得当p≥2时有

(3)

2主要结果

定理1设{Xn,n≥1}是均值为零的END序列，{an,n≥1}为正实数序列且an↑∞。设{gn(t),n≥1}为取正值的偶函数序列。假定存在常数β∈(1,2]及δ>0，使得gn(t)≥δtβ，对01成立。如果

(4)

则有

(5)

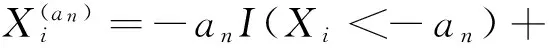
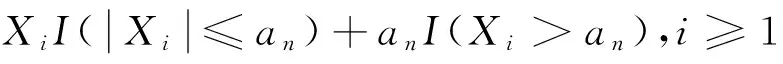
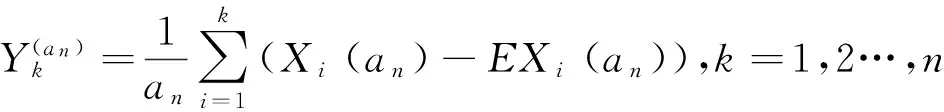
(6)

由(6)式又可推出

(7)

根据已知条件EXi>0，及对t>1，有gn(t)≥δt，可知

将上式结合(5)式，则有

(8)

利用(7)式和(8)式，知对充分大n，有

(9)

因此为证(5)式成立，只需证

(10)

(11)

由(4)式，即有

(10)式得证。

再由已知条件，存在1<β≤2，使得gn(t)≥δtβ，对0

可得

(11)式得证。

结合(9)—(11)式得定理1结论成立。

(12)

则有

注2.1END是一类更宽泛的随机变量序列，它包括独立序列，NA序列及NOD序列等。本文所得结论推广了独立随机变量序列及NOD等相依序列的结论。

[参考文献]

[1]Hsu P L, Robbins H．Complete convergence and the law of large numbers[J]. Proceedings of the National Academy of Sciences of the United States of America，1947, 33(2): 25-31．

[2]Liu L. Precise large deviations for dependent random variables with heavy tails[J]. Statistics and Probability Letters, 2009, 79(9): 1290-1298.

[3]Joag-Dev K, Proschan F. Negative association of random variables with applications[J]. The Annals of Statistics, 1983, 11(1): 286-295.

[4]Ghosh M. Multivariate negative dependence[J]. Communication in Statistics Theory and Methods, 1981, 10: 307-337.

[5]Block H W, Savits T H, Shaked M. Some concepts of negative dependence[J]. The Annals of Statistics, 1982, 10(3): 765-772.

[6]Alam K, Saxena K M L. Positive dependence in multivariate distributions[J]. Communication in Statistics-Theory and Methods, 1981, 10(12): 1183-1196.

[7]Wu Y F, Zhu D J. Convergence properties of partial sums for arrays of rowwise negatively orthant dependent random variables[J]. Journal of the Korean Statistical Society, 2010, 39: 189-197.

[8]Liu L. Necessary and sufficient conditions for moderate deviations of dependent random variables with heavy tails[J]. Science China Mathematics, 2010, 53(6): 1421-1434.

[9]Qiu D H, Chen P Y, Antonini R G, Volodin A. On the complete convergence for arrays of rowwise extended negatively dependent random variables[J]. Journal of the Korean Mathematical Society, 2013, 50(2): 379-392.

[10]Wu Y F, Guan M. Convergence properties of the partial sums for sequences of END random variables[J]. Journal of the Korean Mathematical Society, 2013, 49(6): 1097-1110.

[11]Zhang G Z. Complete convergence for Sung's type weighted sums of END random variables[J]. Journal of Inequalities and Applications, 2014,2014: 353.

Complete Convergence for Sequence of END Random Variable

ZHANG Yongjun

(EditorialDepartmentofJournal，HefeiUniversity,Hefei230601,China)

Abstract：By using some moment inequality for END random variables, some complete convergence theorems for sequence of END random variable are obtained. These results generalize the corresponding theorems for independent sequence and some other type of dependent sequence.

Key words：extended negatively dependent sequence; moment inequality; complete convergence

[收稿日期]2016-02-05

[基金项目]2013年度合肥学院科研发展基金重点项目(13KY05ZD)资助。

[作者简介]张永军(1975-)，男，安徽合肥人，合肥学院学报编辑部副编审。

[中图分类号]O211.4

[文献标识码]A

[文章编号]1674-2273(2016)03-0010-02