折射率椭球主轴化方法探讨

杨　青

(安徽大学 物理与材料科学学院，安徽 合肥 230039)



折射率椭球主轴化方法探讨

杨青

(安徽大学 物理与材料科学学院，安徽 合肥 230039)

[摘要]某些晶体，如铌酸锂，磷酸二氢钾(KDP)等，加上电场后，会改变光在晶体中传播时所表现的各向异性的性质，这种效应称为电光效应。在分析线性电光效应时，一般光电子技术教材中都会采用折射率椭球方程讨论电致折射率的变化，并利用坐标轴旋转法寻找新的折射率椭球的主轴。本文将介绍另一种矩阵理论的方法分析折射率椭球方程主轴化问题，并与坐标轴旋转法进行比较。

[关键词]电光效应；折射率椭球方程；主轴；KDP晶体

1893年Pockels发现，若干晶体，加上电场后，能改变它们的各向异性的性质，引起折射率的变化，此现象称为电光Pockels效应，即线性电光效应。由于其结构简单，易于控制，故在激光通信、激光测量、激光数据处理等领域有着广泛的应用[1-7]。

在光电子技术教程中，电光效应及其应用部分是其中的重点和难点。一般光电子技术教材中分析线性电光效应时，都采用折射率椭球的方法讨论电致折射率的变化，利用坐标轴旋转法寻找新的折射率椭球的主轴[5-7]。这种方法是初等代数的方法，我们这里将介绍一种新的矩阵理论方法对该问题进行研究。本文以KDP晶体为例，分别用上述两种方法分析折射率椭球方程主轴化问题，并对两种方法进行比较。

1折射率椭球

在晶体中沿某一给定方向传播的波的相速度与偏振方向有关。在分析晶体中沿任意方向传播的波时，问题就变得非常复杂，这时采用折射率椭球的方法来分析问题比电磁理论方法更直观方便。

折射率椭球方程是用来描述光波在各向异性晶体中的传播规律的方程。一般在没有外加电场的情况下，晶体的折射率椭球方程是一个正椭球方程，但是根据电磁场理论，一旦加上外电场，光波与介质发生相互作用，引起介质的折射率发生变化，这时电光晶体折射率椭球的主轴不再是原来的主轴，方程变成一般的椭球方程。这时需要寻找新的折射率椭球的主轴，即将新的折射率椭球主轴化。

在晶体未加外电场时，在其主轴坐标系中，折射率椭球方程为：

(1)

式中，x、y、z为介质的主轴方向，即在晶体内沿着这些方向上的电位移和电场强度互相平行；nx,ny,nz为折射率椭球的主折射率。对单轴晶体，一般有nx=ny≠nz；对双轴晶体，则有nx≠ny≠nz。

当晶体施加电场后，其折射率椭球就发生”变形”，椭球方程变为

(2)

可见，由于外加电场的作用，折射率椭球各系数(1/n2)随之发生线性变化。其变化量可定义为

(3)

式中，具有γij元素的6×3矩阵称为电光张量，每个元素的值由具体的晶体决定，它表征感应极化的强弱。利用上式即可算出各系数(1/n2)的变化，进而讨论折射率椭球的变化。下面以KDP晶体为例分析如何将新的折射率椭球主轴化。

2KDP晶体的线性电光效应

(4)

由上式可看出，外加电场导致折射率椭球方程中“交叉”项的出现，椭球的主轴不再与x，y，z轴平行，因此，必须找出一个新的坐标系，使式(4)在该坐标系中主轴化，这样才可以确定电场对光传播的影响。下面按外加电场施加方向分两种情况进行讨论。

2.1外加电场平行于光轴

设外加电场方向平行于z轴(光轴)，即 Ex=Ey=0,Ez≠0，于是(4)式简化为

(5)

为了寻求一个新的主轴坐标系(x′，y′，z′)，使椭球方程不含交叉项，即将新的椭球主轴化。教材上一般采用的是坐标轴旋转法，我们先作简单回顾，然后重点介绍矩阵理论的方法。

2.1.1坐标轴旋转法

由于式(5)中x和y是对称的，故可将x坐标和y坐标绕z轴旋转α角，则新旧坐标系之间的变换关系为

(6)

将式(6)代入式(5)，并令交叉项为零，可算出α=45o，则方程变为

(7)

这就是KDP晶体沿z轴加电场之后的新折射率椭球方程，新的主轴分别为

(8)

由此可见，KDP晶体沿z轴加电场后，由单轴晶体变成了双轴晶体，折射率椭球的主轴绕z轴转了45°角，此转角与外加电场的大小无关，其折射率变化与电场成正比，这就是电光Pockels效应。这是教材上介绍的坐标轴旋转法将折射率椭球主轴化。下面介绍矩阵理论法。

2.1.2矩阵理论法

外加z向电场后晶体的折射率椭球方程(5)式，可用矩阵形式表示为，

(9)

根据矩阵理论[8]，可经过将矩阵对角化，找到一个新的坐标系，使得在这个新的坐标系中，(9)式变成一个对角阵，并通过该形式找出新的折射率。即求满足

(10)

(11)

该方程有非零解的充要条件是其系数行列式不为零，即

(12)

通过计算可以得到三个特征值分别为

(13)

从而得到在新的坐标系下的折射率椭球方程是

(14)

该结果与用坐标系旋转法得到的结果(7)式相同。其后关于新的主轴折射率大小变化的讨论与前面相同，不再赘述。

2.2外加电场垂直于光轴

(15)

同样，分两种方法讨论如何将折射率椭球主轴化。

2.2.1坐标轴旋转法

按照2.1.1类似的步骤，这里由于式(15)中出现了xz交叉项，故可将x坐标和z坐标绕y轴旋转α角，则新旧坐标系之间的变换关系同式(6)，只是y换成了z，于是可得新坐标系下的折射率椭球方程为

(16)

要使上述方程主轴化，需令交叉项的系数等于0，即

(17)

(18)

将上式代入(16)式，可得新主轴坐标系x′y′z′中的折射率椭球方程近似表达式：

(19)

2.2.2矩阵理论法

折射率椭球方程(15)用矩阵形式可写为

(20)

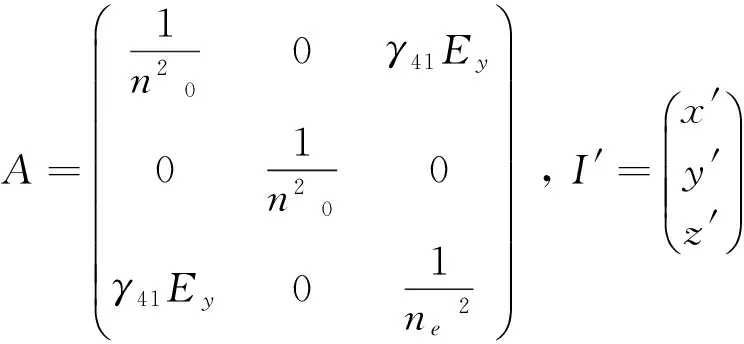
容易求得三个特征值分别为

(21)

于是可以得到新主轴坐标系中的折射率椭球方程为

(22)

该结果和由坐标旋转法得到的(19)式并不完全相同，因为这里没有采用任何近似。

通过计算比较，可知两种理论都可以解决电光效应中折射率椭球方程主轴化的问题。但是在稍微复杂的情形下，坐标旋转法需要采用某种近似才能得到结果，而矩阵理论法则可通过直接求解特征值得到结果。

3结语

我们以KDP晶体为例，介绍了利用坐标轴旋转法和矩阵理论讨论外电场作用下的折射率椭球方程主轴化问题。通过计算与分析，可以得出，在具有较高对称性的简单情形下，采用坐标旋转法简便直观；但是在相对复杂的情况下，利用坐标施转法，必须采用一定的近似，因而，矩阵理论计算更精确更具有普遍性。

[参考文献]

[1]江月松，唐华，何云涛.光电技术[M].北京：北京航空航天大学出版社，2012.

[2]石顺祥，过巳吉.光电子技术及其应用[M].成都：电子科技大学出版社，2000.

[3]裴世鑫，崔芬萍，孙婷婷.光电子技术原理与应用[M].北京：国防工业出版社.2013.

[4]曾光宇，张志伟，张存林. 光电检测技术[M].北京：清华大学出版社.2005.

[5]朱京平.光电子技术基础[M].北京：科学出版社，2009：161-176.

[6]杨小丽.光电子技术基础[M].北京：北京邮电大学出版社，2005：119-130.

[7]安毓英，刘继芳，李庆辉，冯喆珺.光电子技术[M].北京：电子工业出版社，2011：55-60.

[8]戴立辉.线性代数[M].上海：同济大学出版社，2007:159-198.

Discussion on the Spindle of Refractive Index Ellipsoid

YANG Qing

(SchoolofPhysics&MaterialScience,AnhuiUniversity,Hefei230601,China)

Abstract：As we know, when the electric field is added to some crystals, such as LiNO3 and KDP, the anisotropic characteristic of propagation of light wave in the crystal will change, which is called electro-optic effect. As analyzing this effect, the equation of refractive index ellipsoid is usually used to discuss the change of refractivity in general textbooks of optoelectronic technology. Then the method of rotating axis is employed to find the spindle of the new refractive index ellipsoid. Here we present another method by using the theory of matrix to analyze the spindle of the new refractive index ellipsoid by comparing this method with that of rotating axis.

Key words：electro-optic effect；equation of refractive index ellipsoid；spindle; KDP crystal

[收稿日期]2016-01-10

[基金项目]国家自然科学基金(11204002)

[作者简介]杨青：女，博士，安徽大学物理与材料科学学院副教授，从事量子信息与量子计算的研究。

[中图分类号]TN29

[文献标识码]A

[文章编号]1674-2273(2016)03-0016-04