HPM视角下的“三角形的内角和”教学

廖飞 王进敬

摘要：文章运用复制式、顺应式和重构式将数学史融入三角形内角和的教学，从提波特的旋转法出发，让学生经历从绕三个顶点旋转到绕一个顶点旋转，再到绕一边上的任意一点旋转，最后到绕三角形所在平面上任一点旋转的三角形内角和探究过程。

关键词：HPM；三角形的内角和；教学设计；三维目标；反馈

“三角形的内角和”是沪教版《数学》七年级下册的教学内容，之前学生已学习过平行线的性质、三角形相关概念等内容。三角形内角和定理是平面几何学中最重要的三个定理之一。本节课的教学目标：通过旋转法的实验操作、归纳总结、说理论证，让学生经历三角形内角和的探究过程；体会直观感知与理性思考之间的联系和区别，感受数学思维的多样性和灵活性，懂得直观结论需要说理证实的意义；借助数学史，让学生感受数学的悠久历史和多元文化、感受三角形内角和定理背后的人文精神。教学重点及难点是掌握三角形内角和性质的发现与说理方法。

1 历史材料的选择与加工

1.1 提波特旋转方法的历史

古希腊七贤之一、著名哲学家泰勒斯（Thales，公元前6世纪）最早从拼图实践中发现了三角形内角和定理，但这种发现完全是经验性的，泰勒斯并未给出严格的证明。之后，古希腊数学家毕达哥拉斯、欧几里得、普罗克拉斯等相继给出了基于平行线性质的不同的证明；法国数学家帕斯卡、克莱罗，德国数学家提波特等相继给出不同的发现方案。

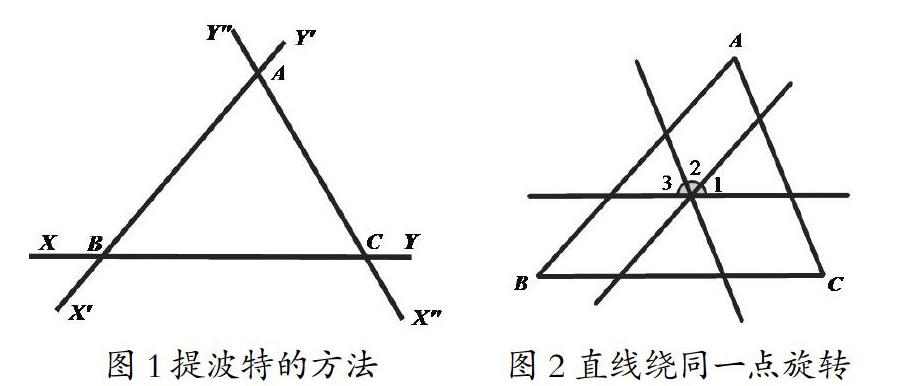
提波特（Thibaut，1775-1832）利用旋转的方法发现了三角形内角和。如图1所示，将BC所在直线XY绕点B沿逆时针方向旋转∠B的度数，到AB所在的直线X'Y'；将X'Y'绕点A沿逆时针方向旋转∠A的度数，到AC所在的直线X"Y"；最后，X"Y"绕点C沿逆时针方向旋转∠C的度数，到直线BC所在直线，总共转过180度。如果考虑顺时针方向旋转，即可证明三角形外角和定理。

19世纪西方平面几何教材大多采用毕达哥拉斯或欧几里得的方法来证明三角形内角和定理，但也有少数教材将毕氏和欧氏的方法推广到一般情形：不在某一顶点处作某一边的平行线，而在三角形内任一点处同时作三条边的平行线，如图2所示，可看作是将提波特的三点旋转改成了一点旋转。用这种方法易于证明三角形外角和定理，并可用于任意多边形。

1.2 历史材料的运用

以旋转方法为主线，让学生经历从“绕三顶点旋转”到“绕同一个顶点旋转”，再到“绕某一边上任一点旋转”，最后到“绕三角形内任一点旋转”的过程，逐一展现了历史上毕达哥拉斯、欧几里得、普罗克拉斯以及19世纪西方几何教科书中的方法，以重构、复制和顺应等方式融入数学史。

2 教学设计与实施

2.1 新课引入

教师演示几何画板，让学生观察三角形的形状变化。问题1 随着三角形形状的变化，单个角的度数是否确定？内角和的度数是否改变？学生很容易地给出答案：单个角的度数不确定，内角和的度数是确定的，三角形的内角和等于180度。

教师抛出本节课的探究任务。问题2 根据已知△ABC，不添加其他条件，说明∠B+∠A+∠C=180？紫。你能解决这个问题吗？学生们感到匪夷所思，认为只有添加条件才能解决问题。教师顺理成章地引出德国数学家提波特的故事，通过几何画板演示了他的旋转方法：将三角形某一边所在直线分别绕三个顶点沿逆时针依次旋转相应角度，验证了“三角形内角和等于180度”。

2.2 用旋转法探究三角形内角和

2.2.1绕同一个顶点旋转

教师首先复习旧知：说明∠B+∠A+∠C=180？紫，在已经学过的知识中，有哪些与180？紫有关？学生一起叙述出平角、邻补角和同旁内角。

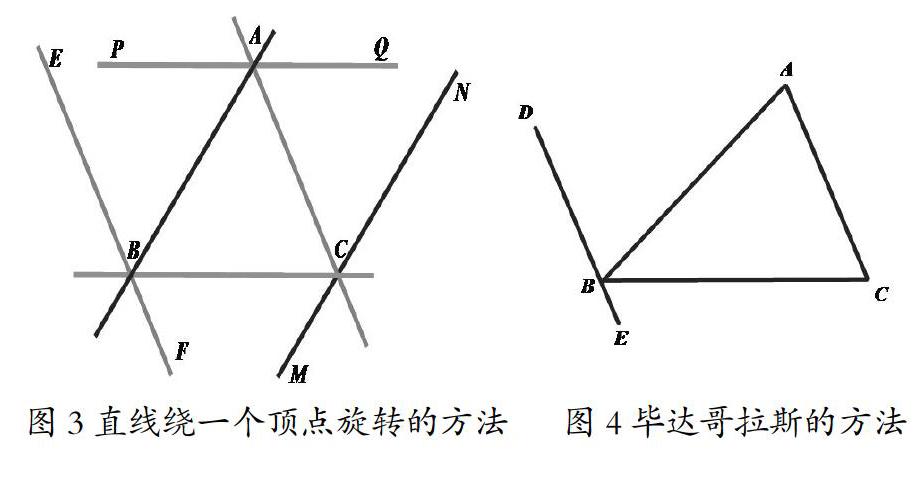
教师引导学生运用提波特的旋转思想，将△ABC的某一边所在直线绕其上某一顶点按逆时针旋转一次，将∠B+∠A+∠C转化为平角或同旁内角。通过师生互相交流，解决了如下问题：提波特的方法是将三角形的边所在直线绕着几个顶点按逆时针旋转呢？能否将某条边所在直线，绕着三角形的一个顶点，按逆时针方向旋转，就可以将∠B+∠A+∠C转化为平角或同旁内角？在前面方法的启发下，请你在任务单上利用操作图①动手完成该操作过程，看看会有什么发现。

通过几何画板演示，三名学生分别选择了AB，AC和BC所在直线进行了旋转（图3）：1.将AB所在的直线绕着点B逆时针旋转∠A的度数，EF∥AC，∠ABE=∠A，∠CBF=∠C，那么∠B+∠A+∠C是一个平角；2.将AC所在直线绕着点A沿逆时针方向旋转∠C的度数，PQ∥BC，∠PAB=∠B，∠QAC=∠C，那么∠B+∠A+∠C是一个平角；3.将BC所在的直线绕着点C逆时针旋转∠B的度数，MN∥AB，得到的结果一样。

师生发现了直线绕一个顶点旋转的所有方法，因其选择边的不同而分成三类，为此选择其中一种方法利用图形进行说理。师生一起叙述，由教师板书毕达哥拉斯方法的严谨说理过程：如图4所示，过三角形ABC的顶点B作AC的平行线，利用两对内错角相等，即得∠ABC+∠A+∠C=∠ABC+∠ABD+∠CBE=180？紫。教师阐述了这个方法是古希腊数学家毕达哥拉斯提出来的，通过探究，激励学生也可以达到他的思维水平，在几何上和他站在同一起跑线上。

通过上述操作还找到了古希腊数学家欧几里得的方法，后期数学家称这种方法宛若从天而降，既神秘又让人佩服。师生共同叙述，由教师在黑板上板书欧几里得方法的说理过程。欧几里得的方法：如图5所示，过点B作CA的平行线BD，则∠ABD=∠A，∠DBE=∠C，故得∠ABC+∠A+∠C为一平角。

教师和学生通过上述的操作一起发现，只要将△ABC的边绕着顶点按逆时针旋转一次就可以将∠B+∠A+∠C转化为平角或同旁内角。并且无论旋转哪条边，本质是相同的。

2.2.2绕某一边上任一点旋转

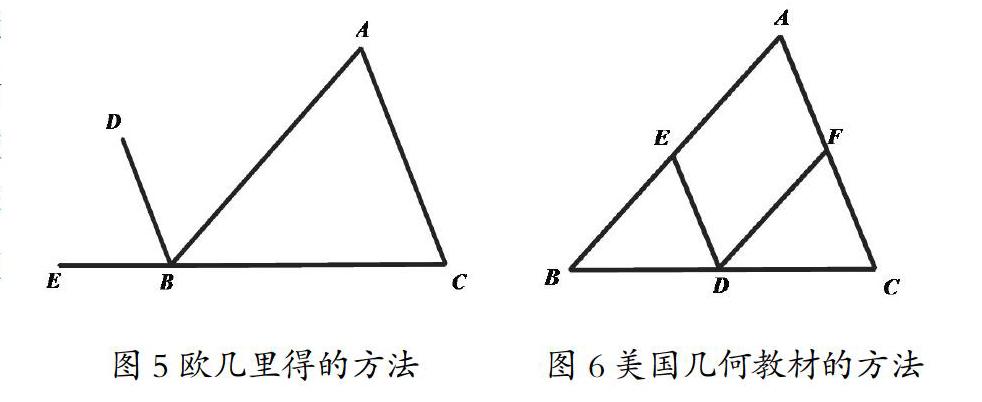
接下来，教师引导学生在任务单上尝试操作，继续探讨BC所在的直线绕着线段BC上任意一点按逆时针方向依次旋转∠B、∠A的度数，将∠B+∠A+∠C转化为平角。教师结合几何画板给学生演示说理过程（图6），指出：19世纪末的美国几何教材上已经出现了该方法。可见，通过探究，站在巨人肩膀上的我们也可以独立得出先哲们曾经用过的证明方法。

师生共同叙述，由教师在黑板上书写添线过程。随后，教师提出课后思考题：绕三角形的边所在直线BC上任意一点按逆时针方向依次旋转两次，可以得到结论吗？要求学生课后在练习本上完成判断并进行说理。

2.2.3绕三角形内任一点旋转

然后，教师提出新的问题：如果将直线BC绕着平面上任意一点按逆时针分别旋转∠B、∠A和∠C的度数，也可以得出三角形内角和等于180度的结论。如果旋转中心选在△ABC的外部，是否可行？教师利用几何画板进行演示，并指出：这种方法已为19世纪西方平面几何教科书所采用（图2）。

教师结合几何画板，介绍了三角形内角和定理的历史，指出：旋转的次数越多，对旋转中心的要求越低，并强调了旋转角度与旋转方向的重要性，再次强调现阶段的学习中，平行线是证明三角形内角和定理的重要工具。最后师生一起归纳了四种方法的共同特征：通过平行线对三角形的内角进行转化，分别将∠B、∠A和∠C转化成具有公共顶点的三个角。

2.3 拓展与总结

教师给出问题：已知AD∥BE，说明∠DAC + ∠EBC =∠C。反之是否成立。首先唤起学生对图7的记忆，问：“如果连接AB，已知AD∥BE，你能说明∠ABC +∠BAC + ∠ACB = 180？紫吗？”教师引导学生通过构造三角形，拓展了平行线性质的应用，得到了古希腊评注家普罗克拉斯的证明方法（图8）：设BD和CE是BC的两条垂线，让BD和CE分别绕点B和点C旋转，使得端点D和点E重合于点A，构成△ABC。原来的两个直角点B和点C所减少的部分相加恰为顶角∠A的大小，即∠ABD +∠ACE =∠A。因此，∠A+∠ABC+∠BCA为两直角之和。

教师以一句话鼓励学生“太阳底下没有新鲜事”，指出三角形内角和定理的证明也是如此，古今中外的数学家们给出了丰富多彩的证明方法，希望有兴趣的同学课后进一步查阅资料、探究新的方法。拓展环节呼应提波特的旋转方法，激发学生感恩意识，锻炼学生语言表达能力，让他们感受、理解和欣赏数学思想之美，体会数学背后火热的思考。

3 学生反馈

课后，对全班35名学生进行了随堂问卷调查。关于“我对老师教学中关于三角形内角和等于180度的启发、引导和发现过程理解得很好”，100%的学生都选择了“同意”或“非常同意”。关于“我愿意了解与教学内容有关的数学历史知识，特别是数学家对问题的思考过程”，97%的同学都选择了“同意”或“非常同意”。关于“这堂课给我提供了一些表达自己想法和展示自己能力的机会”，92%的学生选择了“同意”或“非常同意”。

最后一道开放问题“你还有其他方法吗？有多少写多少”。我们对学生的答案进行了统计分析，1名同学写出4种方法，4名同学写出2种方法，19名同学写出1种方法，11名同学没有想出其他方法。学生的答案分为三角形的内角和性质发现和说理两类方法：（1）直观的发现方法——折纸、撕纸、旋转、测量、三角板，图9～11分别是三名学生各自给出的解答；（2）严谨的说理方法——添加辅助线，利用平行线的性质构造新图形，找到联系已知与未知的桥梁，图12是一名学生给出的解答。

从学生们课堂学习表现和课后问卷反馈可以归纳出学生对这节课的印象有5个方面：新的数学知识；悠久的数学历史；智慧的数学家；巧妙的实验操作；严谨的说理方法。

4 结语

本节课以旋转方法为主线，通过旋转中心的改变展开教学，整体上说是对历史的重构。教学过程中，同时又复制了毕达哥拉斯、欧几里得和普罗克拉斯的说理方法。基于课堂观察和学生反馈的结果，数学史知识给学生留下了深刻印象，学生看到“旋转”之美，领略方法之妙，拓宽数学思维，感受多元文化。培养学生的几何直观与想象、推理能力等数学素养。由于数学史的融入，经历旋转法实验发现三角形的内角和性质，添加辅助线进行说理，了解几何学的价值，拉近学生与古代数学家之间的“心理距离”，体会数学的悠久历史与人类文明的密切关系，使数学课堂充满亲和力，培养学生对数学的好奇心和求知欲，提高学生合作交流的能力，创造学生的学习动机，激发学生对数学的兴趣。对教师的访谈和对学生的问卷调查都表明，本节课完成了“知识与技能”“过程与方法”“情感、态度与价值观”的三维教学目标，达到了理想的效果，取得了较大的成功，受到了一致的认可。

参考文献：

[1]汪晓勤.三角形内角和定理：从历史到课堂[J].中学数学月刊，2012，（6）：38-40.

[2]汪晓勤.HPM视角下的“角平分线”教学[J].教育研究与评论（中学教育教学），2014，（5）： 29-32.

[3]Smith D E.The Teaching of Geometry[M].Boston： Ginn and Gompany，1911.184-188.

[4]汪晓勤.HPM的若干研究与展望[J].中学数学月刊， 2012， （2）：1-4.

8