让问题“触网”，养“活”数学思维

陈安燕

【摘 要】学困生头脑中的知识是零散的和孤立的，呈现水平排列方式、列举方式，而学优生头脑中的知识是有组织和系统的，知识点按层次排列，并且知识点之间有内在联系，呈现出一个层次网络结构。可见，形成有序的知识网络结构对学好数学是非常重要的，本文试从如何建构有序的知识网络结构入手，让学生造就一个“强大的头脑”，培养学生学习数学的“超”能力！

【关键词】知识网络 概念图 触网 “超”能力

“老师，你上课说的题目我都听得懂，但是自己做题的时候就不会解题，这是为什么呢？”这是我所教的班级中，学困生常常问我的问题。“这道题都讲过N遍了，学生还是不会，真是被他们气死了！”这是我在办公室常常听老师们抱怨的話语。

这是为什么呢？是因为老师聪明，还是是因为学生笨？都不是，而是因为在老师的脑海中有庞大的、严格有序的、立体系统的知识网络。而在学生的脑中却是一个个无序的、孤立的、零碎的知识点，从而使得正常的解题思路无法展开。

那么如何在数学教学中短时间有效地构建学生自己的知识网络，使学困生碰到不熟悉的数学问题时，让问题“触网”，养“活”他们的数学思维呢？我认为概念图是一个有效的工具。

一、概念图的理论基础

概念图是由美国心理学家FosephD.NOVA于上世纪60年代提出的，是表示知识结构的图示，主要呈现以概念为联结点的网络化知识系统，其理论依据是现代认知心理学的学习观和知识观。

1.意义学习——知识网络的建构过程

现代心理学认为，只有将新知识与已有知识联系在一起，即将新知识结合到认知结构中学习才是有意义的。换句话说学习实际上是学生在头脑中主动建构自己的知识网络的过程，当学生将新知识与旧知识正确的联系在一起，新知识即成为其已有知识网络中的一个新的联络点和知识增长点，整和到其认知结构中，储存在长时的记忆中。因而意义学习才能有效的促进学生的认知策略的形成。

2.概念学习是学习中的关键因素。

知识是由概念组成的。由概念构成命题、知识结构和有意义的学习是学习的核心要素。最好的学习是把概念和命题作为个人理解的基础，因此其意义学习也可理解为：只有当学生有意识地努力确定新知识中的关键概念，并且将其与自己头脑中已有的其他概念联系在一起，形成以命题相联结的概念间广泛联系的知识组块时，才会发生真正的学习，即完成知识的建构，否则仅有孤立概念的记忆存储，则知识是死的、机械的、无意义的，很快就会被遗忘。

二、在数学教学中运用概念图建构学生的知识网络

在现行的高中数学教材中知识点众多，各知识点之间的联系错综复杂，用概念图构建的网络来表达数学知识，对学生掌握各知识点之间的相互关系所起的主导作用，都可以一目了然。那么在数学教学中老师如何帮助学生建构自己的数学知识网络呢？

1.要有建构的意识

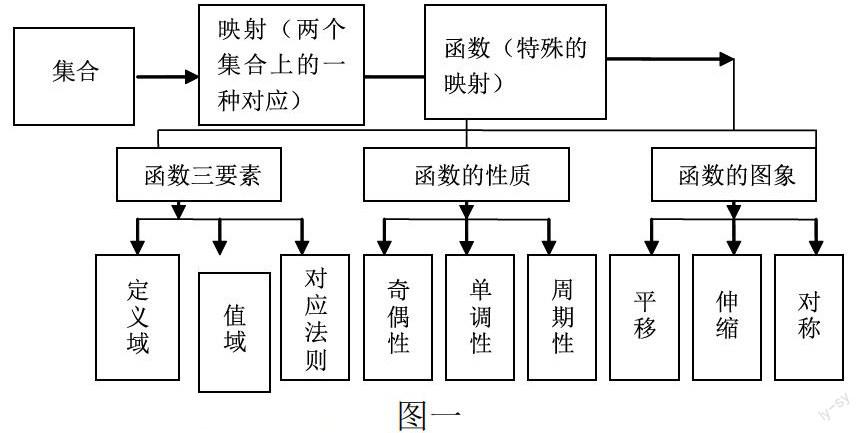
首先要有建构的意识，而不是等到高三以后才注意系统地整理知识，例如在高一始就明确告诉学生本章应该学到的知识，建立起如下概念图（如图一）。学生可以感觉到这些知识不是孤立的，而是一环扣一环。在这个基础之上建立起一个发展的平台，而这个平台又有五大支柱，即幂函数、指数函数、对数函数、三角函数、反三角函数。每一个函数的各项性质就象一个个层面，从而建立起一个立体的网络框架。

2.其次要注意利用概念图培养学生构建网络的能力

将综合性概念图作为一种教学策略应用于数学教学中，教师可采用小组讨论、师生对话或者是学生独立作业等灵活多样的形式。概念图策略即可用于新课的教学，更适合于旧课的复习。

（1）激活旧知识，重视新知识与旧知识的联系

例如在学习《数列》这章的时候对数列的通项公式以及前n项的和时，可以让学生将所学的新知识融入到已学的旧

知识——《函数》中去，将等差数列的通项看成是一次函数；将等比数列看作是变化后的指数函数，将等差数列的前n项和看作是一元二次函数的延伸……许多问题在这个网络中都可以得到迎刃而解。

例如：当数列取得最大值时，求n的值

若学生只知道用纯数列的方法去解答该题时，一定会碰到困难，我曾经在上课的时候让学生求解这道题，几乎全部的学生都说要借助计算器，否则无法完成。然后我给了他们适当的点拨：如果能把这个题目的n看成自变量x，再结合数列和函数的联系去试试。结果绝大部分的学生都恍然大悟，无需计算器的帮助轻松求得答案。从这个题中，学生可以深刻的体会到，利用数列和函数可以类比的这张知识网络，那么这个题目就可以转化为反比例函数求最值，轻松求得答案为44.这就是我们所说的让数学问题“触网”，从而养“活”学生的数学思维！

（2）精心提炼，将知识系统化

一般的，老师在教学中可以让学生先确定要呈现的关键概念，然后编织一张重要概念的清单，其中包括从最普通的、包容性强的概念到最特殊的概念，对其加以排列，使学生明辨信息，帮助他解读其中的涵义。例如在高三《函数图象》复习完成之后，辅导学生自行构建一张详细的概念图，充实到原有的系统中去。

3.运用概念图，提高学生的解题能力

构建了网络不等于就一定能制胜，还有一个实施的过程。合理的知识结构可以在运用时，快速、准确地提取有效的知识。学生是否真正把知识学到手了，要用“运用”来检查。如果学了许多知识但不能在“运用中”表现出来，所储存的知识不能根据需要成为进一步学习和解决实际问题的智慧和力量，那就是没有把知识学到手。而引导学生建立合理的知识结构，就是为了帮助学生快速提取，充分运用已掌握的知识，使知识发挥作用。在这个过程中，可能会遇到困难，此时学生就需要稳定情绪，在广阔的知识背景中迅速的检索，提取有力的武器，将所求的问题“触网”，养“活”求解数学问题的思维。

参考文献

[1]赵国忠：《中国教学的奇迹》，南京大学出版社，2013年12月第1版

[2]涂荣豹、宁连华：《中学数学经典教学方法》，福建教育出版社，2011年6月第1版