备件可靠性分析及需求预测

李田科，李　伟，沙卫晓，于仕财

(1.中国人民解放军91980部队，山东 烟台　264000；2.海军航空工程学院 电子信息工程系，山东 烟台　264000)



备件可靠性分析及需求预测

李田科1，李伟1，沙卫晓1，于仕财2

(1.中国人民解放军91980部队，山东 烟台264000；2.海军航空工程学院 电子信息工程系，山东 烟台264000)

摘要：针对备件需求量确定难的问题，采用可靠性分析法，提出了设备寿命服从多种分布的分布参数估计和未知寿命分布设备的寿命分布假设检验方法，建立了不同寿命分布设备备件需求量的预测模型，编制了装备备件保障软件，可方便、准确预测备件需求。

关键词：备品备件；可靠性；需求

备件是武器系统维修保障的基础，是保障武器系统发挥战斗力的重要组成部分,备件短缺会影响战斗力的发挥，加大储备量，增加费用开支。备品备件需求的预测目标是既满足维修需要，又不造成库存备件积压。

1装备可靠性分析的寿命分布函数

可靠性分析中，对产品平均寿命MTBF进行估算时，常用的寿命分布函数[1-2]如下：

1) 指数分布

式中MTBF为参数λ(λ为大于0的常数)的倒数。

2) 正态分布

E(T)=μ=MTBF

式中μ为随机变量增值。

3) 对数正态分布

式中σ2是随机变量方差。

4) 威布尔分布

式中η>0是比例参数 ，m>0是形状参数。

2分布参数估计与寿命评估

大部分装备故障样本比较少，可用参数法对装备的可靠性指标进行评定。

2.1指数分布的参数估计与寿命评估

寿命服从指数分布，则寿命分布的密度函数f(t)为

1) 极大似然估计(点估计)

抽取n个产品进行有替换时截尾试验，截尾时间为t0，在试验中，观察结果是：在[0，t0]内有r个产品失效，其失效时间依次为t1≤t2≤…tr，则似然函数应为(推导过程略)

式中s(t0)为到t0时刻总试验时间。

式中s(tr)为到tr时刻产品的总试验时间。

MTBF是对寿命的点估计，但不能反映估计的可信程度，还要寻找λ区间估计(或置信下限)，可给出MTBF的可信程度。

2) 单侧置信下限估计

以对n个产品进行有替换定数截尾试验为例进行论述，截尾时间为tr，t1≤t2≤…tr

其中：r为常数；tr可以改写为

利用次序统计量的分布可证明(略)：诸差t1-t0，t2-t1，…，tr-tr-1都服从参数为nλ的指数分布，且相互独立，即

即2λS(tr)的分布是自由度为2r的χ2分布，则当置信水平为1-α时，λ的单侧置信上限为

平均寿命的单侧置信下限为

当对n个产品进行有替换定时截尾试验时，λ的单侧置信上限为

平均寿命的单侧置信下限为

2.2正态分布的参数估计与寿命评估

寿命服从正态分布N(μ,σ2)，则

对参数μ，σ做出估计。

1) 简单线性无偏估计

经过计算推导，得到的无偏估计为

2) 置信区间估计

由于T服从正态分布N(μ,σ2)，在正态分布下，μ的置信区间为

σ的置信区间为

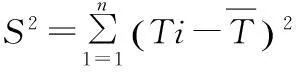
2.3威布尔分布的参数估计与寿命评估

对威布尔分布的参数η，m做出估计。

1) 最小二乘估计法(点估计)

线性化即得

A=-mlnηB=m

则y=mx+A=Bx+A。

x与y线性相关，可根据一组样本观测值(ti,F(ti)),i=1,2,…,n,通过公式相应求得一组(xi,yi)，再由线性回归方程确定出参数A，B和相关系数rg。n为样本总数，i为寿命数据由小到大顺序号：

2) 参数的区间估计

对定数截尾的情况，采用无信息先验分布下的Bayes方法，可提高6倍以上的精度，而且不受样本量及截尾数的限制。

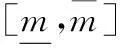
式中

η的Bayes下限ηL为

3装备寿命分布的假设检验

确定某种零件是否一定属于某种分布，需进行分布的拟合检验(由部队统计的零件故障数据作为检验样本)。

3.1指数分布的拟合检验

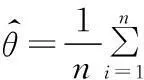
取检验统计量为

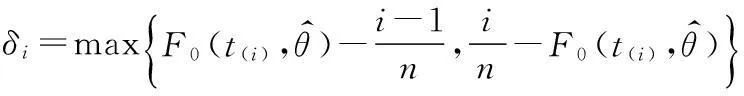
t(1)≤t(2)≤…≤t(n)是子样(t1≤t2≤…≤tn)的次序统计量。

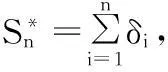
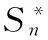
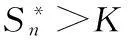
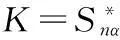
3.2正态分布的拟合检验

取检验统计量为

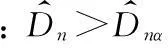
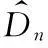
3.3威布尔分布的拟合检验

设产品的寿命分布为F(t)，要检验假设

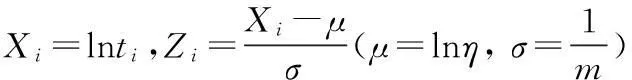
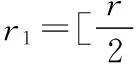
4基于备件寿命分布备件需求量

4.1指数寿命件备件量计算模型

若装备中某项零部件的寿命服从指数分布，为满足规定保障概率P，该项零部件的备件需求量计算式为[6]

式中：s为某零部件所需备件数；N为某零部件的件数；λ为某零部件的失效率，10-6/h；t为鉴于泊松方程的通用性，t可据情况分别处理；j为递增变量，j从0开始增加，使得p(j≤s)大于规定值，该s值即为所求之备件数量；p为备件保障概率。

4.2正态寿命件备件量计算模型

已知正态寿命件均值E，标准差σ，更换周期t和备件保障概率p，单项件备件需求量SN

其中up为正态分位数，可查正态分布表得。

4.3寿命服从威布尔分布的备件量计算模型

1) 某部件寿命分布为3个参数威布尔分布：

2) 需要该部件时，能得到它的概率为P，并设此事件(即“部件故障时能得到满足”)服从正态分布；

3) 单部装备累积工作时间为T；

4) 该部件共有L个；

5) 该部件可修复，修复率为μ(当μ=0时，表示该部件不可修)；

在单个装备累积工作时间≤T，备件满足率为P，需为M个装备提供该备件的个数S的计算模型如下

式中μp为正态分位数，可查正态分布表得；E，σ2：设备寿命的均值和方差：

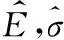
5装备备件保障软件

备件保障软件可根据设备前期的故障信息利用上述统计方法分析设备的寿命分布和故障率，并用预测模型预测备件的需求量。使用时只需提供装备的故障数据、保障概率、保障时间和设备数量即可预测备件需求量，其预测流程如图1所示。

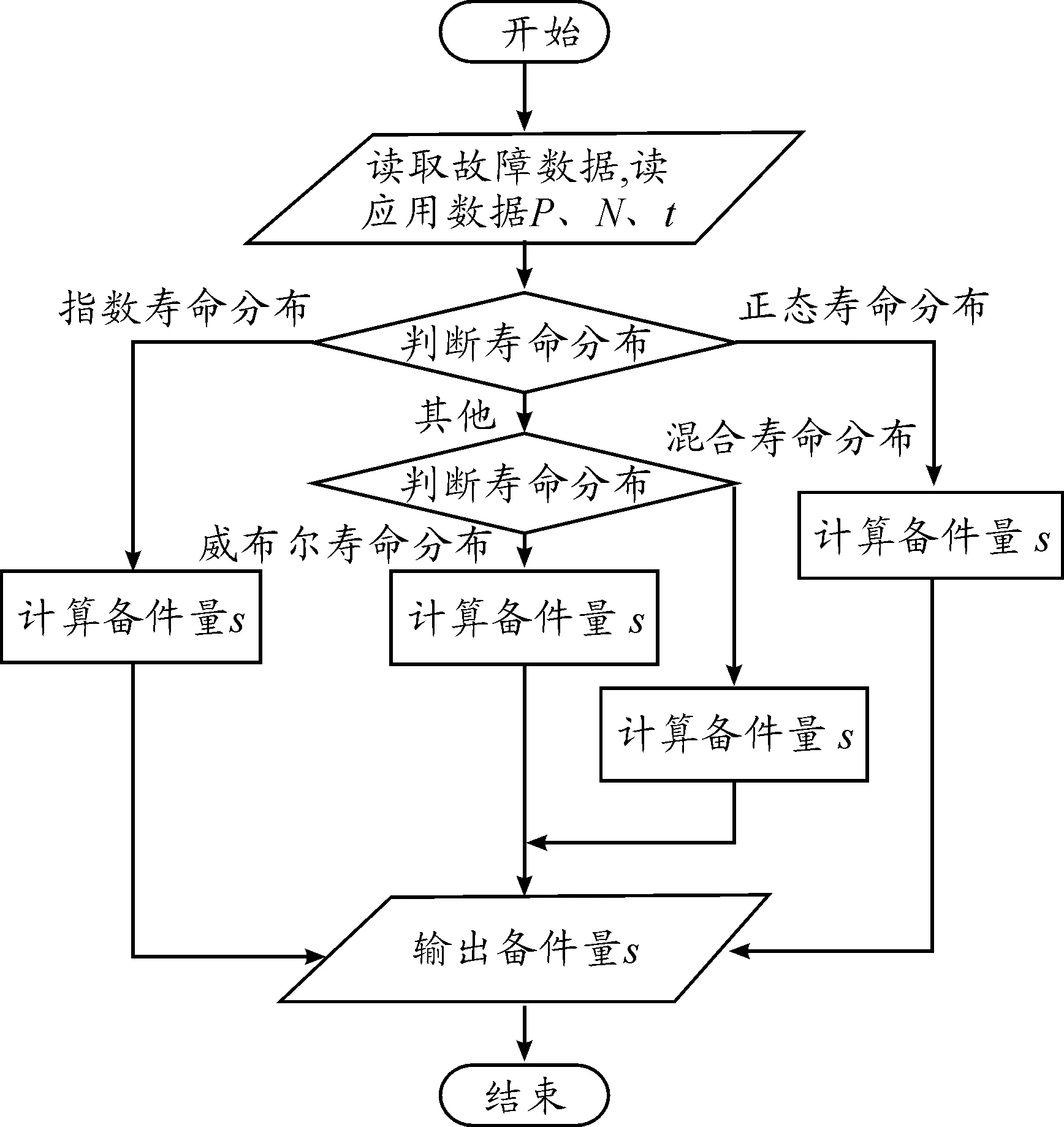
图1　依统计数据备件预测流程

6软件应用实例分析

下面以导弹发射车为例，应用统计数据预测备件需求量进行分析。

某系统某电路插板，单车安装数为1个，共2辆车，备件的计划保障概率为90%，统计到的故障间隔时间记录如下(单位h)：

1：1 410，1 500，12 520，15 350；

2：2 062，6 930，7 150，14 660，18 260。

由软件统计得出，此插板的工作寿命服从指数分布，平均寿命8 871.33 h；下面分别计算不同条件下此插板的备件需求量。

1) 单车出战时备件携行量计算

通过软件计算得出备件需求量与保障概率和保障时间之间的关系如表1所示。

表1　单车出战时备件需求

由表1可以看出，单车出动时，要求保障概率为90%，携带1个备件的情况下，可满足设备工作时间不超过934 h；设备工作时间小于3 164 h，携带1个备件能满足70%的保障概率。

2) 双车出战时备件携行量计算

通过软件计算并得出备件需求量与保障概率和保障时间的关系如表2所示。

表2　双车协同出战时备件需求

根据表2所示，当双车出战时，要求保障概率为90%，携带1个该插板备件的情况下，可满足工作时间不超过467 h，出战工作时间在468～2 358 h内需携带2个备件；大于2 358 h需携带3个该备件。

7结束语

以装备可靠性、维修性等因素为基础建立的备件需求量预测模型，对各种类型的设备进行备件需求预测。从可靠性出发又解决了备件保障概率问题，可准确确定出为达到一定保障概率所需储备的备件量。用计算机辅助备件需求预测工作，使备件预测工作更准确、方便，将极大地提高部队的备件保障能力。

参考文献：

[1]赵建忠，朱伟，徐恒博,等.基于故障规律的导弹备件消耗预测[J]．战术导弹技术,2012(5):44-49.

[2]董琪，徐廷学，赵建忠,等.基于调拨方案的两级库存备件优化配置研究[J]．战术导弹技术,2014(3):12-16.

[3]邵延君，马春茂，潘宏侠,等.基于GERT的武器装备维修备件订货间隔期预测[J]．火力与指挥控制,2015,40(4):38-40.

[4]邵延君，马春茂，潘宏侠,等.基于寿命周期备件费用的系统可靠性优化设计[J]．中国工程科学,2015,17(5):25-29.

[5]张帅，唐金国，孙媛,等.舰载机有限可修复备件库存模型[J]．兵工自动化,2015,34(3):10-12.

[6]应新雅，张志华，金正.系统备件利用率及备件配置方案优化[J]．指挥控制与仿真,2015,37(2):134-137.

[7]王正元， 曹继平， 朱昱，等.考虑维修能力的战时备件资源配置方法研究[J].兵工学报，2014(5):719-724.

(责任编辑唐定国)

本文引用格式：李田科，李伟，沙卫晓，等.备件可靠性分析及需求预测[J].兵器装备工程学报，2016(4):47-50.

Citation format:LI Tian-ke, LI Wei, SHA Wei-xiao, et al.Spare Part Reliability Analysis and Demand Prediction[J].Journal of Ordnance Equipment Engineering,2016(4):47-50.

Spare Part Reliability Analysis and Demand Prediction

LI Tian-ke1, LI Wei1, SHA Wei-xiao1, YU Shi-cai2

(1.The No. 91980thTroop of PLA, Yantai 264000, China;2.Department of Electronic and Information Engineering,Naval Aeronautical Engineering Institute, Yantai 264000, China)

Abstract:According to the difficulty of spare part’s determination, this paper proposed method of distribution parameter estimation for equipment which the life submits many distributions and hypothesis testing method for equipment which life distribution unknown by using reliability analysis. It built the forecast model of the spare part requirement of equipment which the life submits different distribution, and made the software of weapons spare part support, which makes the spare part’s prediction become more exact and easier.

Key words:spare part; reliability; requirement

文章编号：1006-0707(2016)04-0047-05

中图分类号：TJ765.4

文献标识码：A

doi:10.11809/scbgxb2016.04.013

作者简介：李田科(1976—)，男，硕士，高级工程师，主要从事导弹装备保障研究。

收稿日期：2015-10-20；修回日期：2015-11-21

【后勤保障与装备管理】