锐角三角函数考法展示及破解策略

余中华

锐焦三角函数的内容可分为两个部分：第一部分是正弦、余弦和正切的基本概念，特殊角的三角函数值；第二部分是解直角三角形及其应用.

1.中考考情分析

人教版教材一共有356课时，其中锐角三角函数一章一共安排了12课时，尽管本章内容所占的课时比例少了点，但锐角三角函数却是中考试卷的高频考点，

为什么解直角三角形在中考试卷中出现的频率如此之高呢？原因有两个：（1）解直角三角形代表的是一类应用问题，而且是几何知识的应用，要让学生感觉到数学知识学有所用，那么中考试卷就必须要出现应用问题.（2）高中阶段，将要学习三角知识（解斜三角形，三角函数），因此锐角三角函数是继续学习高中知识的需要，

通过对各地中考试卷分析，可以看出在中考试卷中，本章在中考试卷中常常会以一道解直角三角形的应用问题的形式出现，偶尔可能以一道简单的填空或选择题的形式出现.

2.锐角三角函数的基本概念是填空、选择题的高频考点

2.1深刻理解正弦、余弦、正切概念

给定直角三角形，求一个角的正弦、余弦、正切的值，或者通过构造直角三角形求已知角的三角函数值，或者通过求相等角的三角函数值来解.

例1 （2014年广东广州卷）如图1，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA=（

）

A.3/5

B.4/5

C.3/4

D.4/3

答案：D.

评注：本题已经给定了Rt△ABC，直接利用正切的定义求解即可，理解锐角三角函数的定义是解决此类问题的关键.

评注：本题需要构造直角三角形，可借助垂径定理.连接OB，OC，过点O作OD⊥BC于D.如图2根据圆周角和圆心角的关系可得到∠BOD与∠A相等，进而可将求∠A的正切值转化为求∠BOD的正切值.

启示：求锐角三角函数值必须在直角三角形中计算，如果图中没有直角三角形，可考虑作辅助线，通过构造直角三角形来解决问题，

2.2 特殊角的锐角三角函数是中考关注的焦点

特殊的锐角三角函数常见考法有两种：一是直接写出特殊角的三角函数值；二是由特殊角的三角函数值推断出角的度数.

答案：A.

评注：本题是直接写出60。的余弦，虽然简单，但类似的考法在中考试卷中时常出现.

评注：本题是已知一些角的三角函数值，逆推这些角的度数，这些值一般是特殊角的三角函数值.

2.3 锐角三角函数基本概念与其他几何知识的综合

在2014年中考试卷中，除了直接考查正弦、余弦、正切的概念外，还出现了一些与四边形、圆等知识整合在一起的综合问题.

答案：B.（提示：本题可通过作辅助线，再利用切线的性质、三角形相似及勾股定理进行求解.辅助线的作法：连接OA，OB，OP，延长BO交PA的延长线于F.）

评注：直接考查锐角三角函数知识，或者考查解直角三角形，一般难度都不是很大，如果要提升难度，那么只能与其他知识综合起来.本题就是一道直线与圆的位置关系和正切概念的综合题，题目的难度明显提升，所以本题放在选择题的最后一题，事实上，本题所用的锐角三角函数知识很简单.

3.应用问题考法展示及破解策略

解有关直角三角形的实际应用问题是中考几乎必考的知识点之一，这类问题的解题策略是将实际问题抽象为一个数学问题.抽象得到的几何图形可能是一个直角三角形，此时题目比较简单，一般出现在填空、选择题中，直接应用正弦、余弦、正切的定义解决问题即可；得到的几何图形也可能是一个锐角三角形或其他特殊的图形，这时可通过构造垂线段，将图形转化为两个或多个直角三角形.

3.1 构造单直角三角形问题

3.2 构造双直角三角形问题

答：海警船到达C处需1. 25小时.

评注：从这道题的解答过程可以看出，构造得到的两个直角三角形Rt△BCD和Rt△ACD具有公共边CD，通过CD这条公共边建立起这两个直角三角形之间的联系.因此解决此类问题，建立起两直角三角形的联系是解决问题的关键.再如下面这道题目：

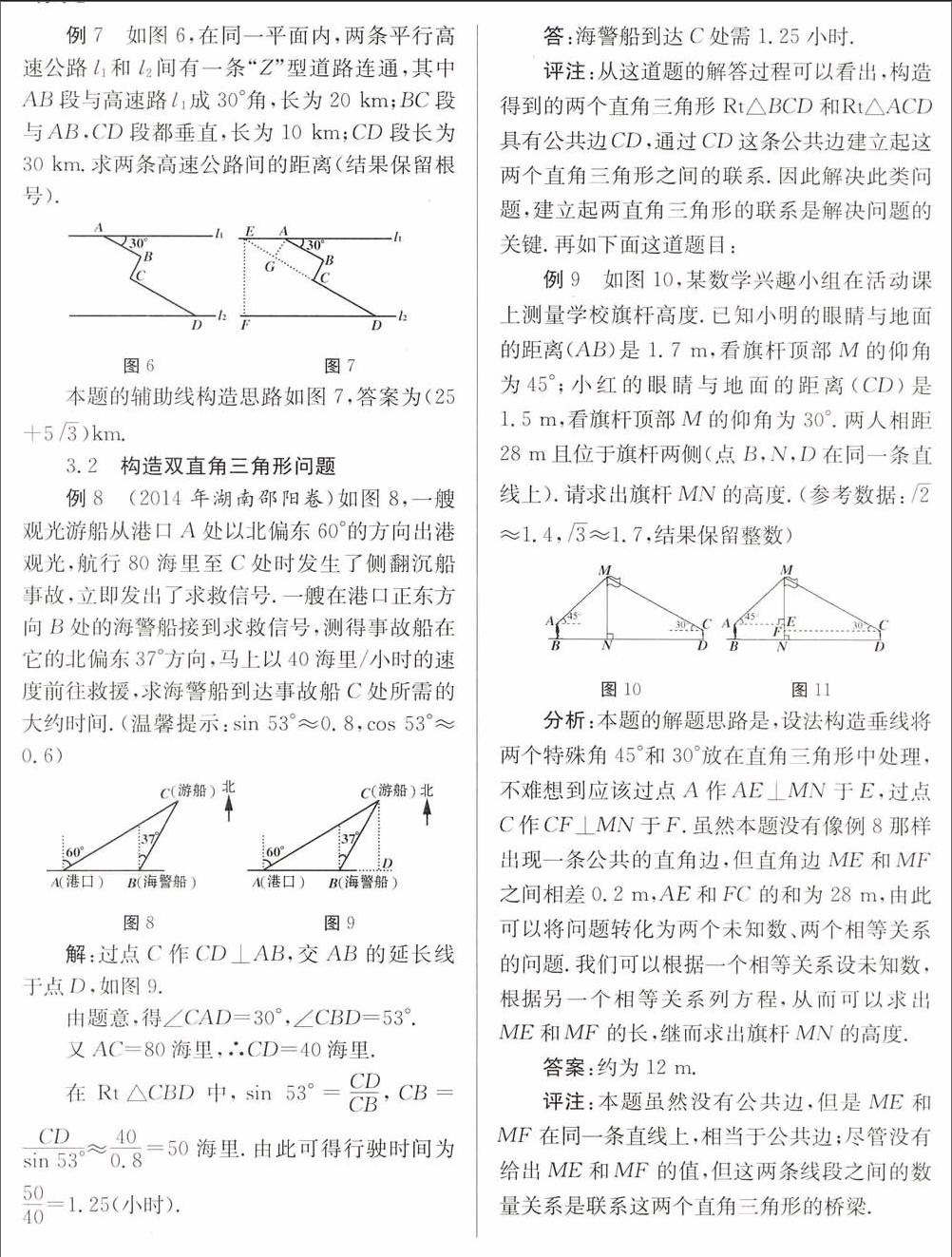
分析：本题的解题思路是，设法构造垂线将两个特殊角45°和30°放在直角三角形中处理，不难想到应该过点A作AE⊥MN于E，过点C作CF⊥MN于F.虽然本题没有像例8那样出现一条公共的直角边，但直角边ME和MF之间相差0.2m，AE和FC的和为28m，由此可以将问题转化为两个未知数、两个相等关系的问题，我们可以根据一个相等关系设未知数，根据另一个相等关系列方程，从而可以求出ME和MF的长，继而求出旗杆MN的高度，

答案：约为12m.

评注：本题虽然没有公共边，但是ME和MF在同一条直线上，相当于公共边；尽管没有给出ME和MF的值，但这两条线段之间的数量关系是联系这两个直角三角形的桥梁.