任意Bell型纠缠态的双向受控概率隐形传态

王小宇, 莫智文

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

任意Bell型纠缠态的双向受控概率隐形传态

王小宇, 莫智文*

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

提出一种利用非最大纠缠态作为量子信道,实现任意Bell型纠缠态的双向受控概率隐形传态.通信双方Alice、Bob和控制方Charlie事先密享纠缠态构建量子信道.通信开始后,Alice和Bob分别对自己拥有的个别粒子做测量,并通过经典信道公布结果,若控制方同意双方通信则对自己的粒子做测量,将结果通过经典信道公布.通信双方根据所有测量的结果对各自粒子做相应的幺正变换,引入辅助粒子完成投影测量或者POVM测量,最后再引入辅助粒子实现双向隐形传态.

纠缠态; 幺正变换; 双向传态; 投影测量

1 预备知识

量子通信是量子论与通信论相结合的一门新型交叉科学,主要涉及量子密码通信,量子远程传态和量子密集编码等研究领域,其中量子隐形传态又是最引人瞩目的课题之一.C. H. Bennett等[1]提出了量子隐形传态的概念,是一种利用经典信道和量子纠缠资源实现远程传态的方式[2].学者已经提出了许多传送未知量子态的方案,比如单粒子态、多粒子态的隐形传态、单向受控隐形传态[3]、双向隐形传态[4-6]、概率隐形传态等.X. W. Zha等[7]提出第一个量子双向受控隐形传态方案,作为量子隐形传态的一个新领域,受到极大的关注.一些利用多粒子纠缠态作为量子信道的双向受控隐形传态方案[7-15]已经被提出来,但是这些方案都是针对任意单粒子的隐形传态方案.

M.H.Sang[16]通过利用七粒子纠缠态作为量子信道实现任意单粒子与二粒子态的双向受控隐形传态.迄今为止,关于任意Bell型纠缠态的双向概率量子隐形传态方案还没有研究,并且在实验中制备的纠缠态一般都是非最大纠缠,最大纠缠态很难制备.基于以上这些情况,本文提出一种任意Bell型纠缠态的双向受控概率隐形传态方案.

2 实现受控双向概率隐形传态方案

2.1 控制方为单粒子的受控双向概率隐形传态 当控制方为单粒子时,选用五粒子非最大纠缠态做为量子信道,实现任意Bell型纠缠态的传输.文献[8]给出了一个五粒子纠缠态作为的量子信道实现双向受控隐形传态方案,量子信道可以表示为

|ψ3〉A1B1|ψ4〉A2B2|b〉C1),

(1)

假设Alice和Bob有待传态为

|ζ〉AA′=(a0|00〉+a1|11〉),

|η〉BB′=(b0|00〉+b1|11〉),

(2)

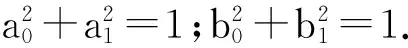
|ψ〉A1A2B1B2C=

(α|00〉+β|11〉)A2B2⊗|0〉+

(α|00〉-β|11〉)A2B2⊗|1〉,

(3)

其中,系数均为非零实数,并且满足α2+β2=1,α>β.粒子A、A′、A1、A2属于Alice,粒子B、B′、B1、B2属于Bob,粒子C属于Charlie.整个系统初态为

|ψ〉AA′A1A2BB′B1B2C=

|ζ〉AA′⊗|ψ〉A1A2B1B2C⊗|η〉BB′.

(4)

首先,Alice和Bob分别对粒子(A,A′,A1)和(B,B′,B1)作正交基三粒子量子联合测量,其测量基如下:

(5)

Alice和Bob通过经典信道把测量的结果公布给对方,若Charlie同意双方通信则对粒子做|0〉、|1〉基测量,并对双方公布测量结果.三方测量后,系统坍缩为如下32种结果之一:

〈0|〈μ±|〈φ±|ψ〉=

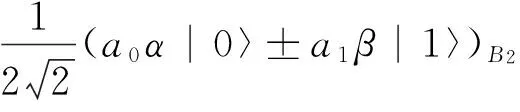
(b0α|0〉±b1β|1〉)A2,

〈1|〈μ±|〈φ∓|ψ〉=

(b0α|0〉∓b1β|1〉)A2,

〈0|〈ν±|〈φ±|ψ〉=

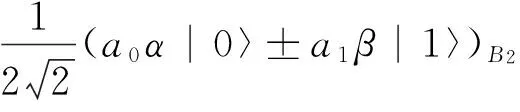
(b0β|1〉±b1α|0〉)A2,

〈1|〈ν±|〈φ∓|ψ〉=

(-b0β|1〉±b1α|0〉)A2,

〈0|〈μ±|〈φ±|ψ〉=

(b0α|0〉±b1β|1〉)A2,

〈1|〈μ±|〈φ±|ψ〉=

(b0α|0〉∓b1β|1〉)A2,

〈0|〈ν±|〈φ±|ψ〉=

(b0β|1〉±b1α|0〉)A2,

〈1|〈ν±|〈φ±|ψ〉=

(b0β|1〉∓b1α|0〉)A2.

(6)

Alice和Bob根据获得的信息对粒子A2、B2做相应幺正变换(见表1),其中

σI=|0〉〈0|+|1〉〈1|,

σZ=|0〉〈0|-|1〉〈1|,

σX=|0〉〈1|+|1〉〈0|.

表 1 三方测量结果以及对应幺正变换

假设Alice、Bob和Charlie测量结果为|φ+〉、|μ-〉、|0〉,粒子A2、B2坍缩为

(a0α|0〉+a1β|1〉).

(7)

然后Alice对粒子A2作σZ变换,Bob对粒子B2作σI变换得

(a0α|0〉+a1β|1〉).

(8)

为了重构原始态,Alice和Bob分别引入一个初态为|0〉的辅助粒子A3、B3,Alice在基{|00〉A2A3,|01〉A2A3,|10〉A2A3,|11〉A2A3}下对粒子A2、A3进行适当的酉变换.Bob在基{|00〉B2B3,|01〉B2B3,|10〉B2B3,|11〉B2B3}下对粒子B2、B3进行酉变换.酉矩阵为

(9)

在U变换下,粒子A2、A3将演变为如下形式

β(b0|0〉+b1|1〉)A2⊗|0〉A3+

(10)

在U变换下,粒子B2、B3将演变为

β(a0|0〉+a1|1〉)B1⊗|0〉B3+

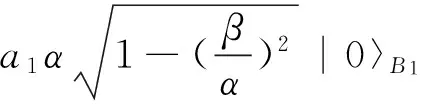
(11)

2.2 控制方为2个粒子的受控双向概率隐形传态控制方为单粒子时能够实现双向隐形传态,当改变控制方的粒子个数时,同样也可以实现双向传输.当控制方粒子为2个时,选择2对非最大三粒子纠缠态作为量子信道.

此时通信双方Alice、Bob与控制方Charlie共享一个六粒子纠缠态为量子信道,表达式为

|ψ〉A1A2B1B2C1C2=(α|000〉+β|111〉)A1B2C1⊗

(x|000〉+y|111〉)B1A2C2,

(12)

其中,系数均为非零实数且满足(α2+β2)=1,(x2+y2)=1,α>β,x>y.粒子A、A′、A1、A2属于Alice,粒子B、B′、B1、B2属于Bob,粒子C1、C2属于Charlie.整个系统的初态为

|ψ〉AA′A1A2BB′B1B2C1C2=

|ζ〉AA′⊗|ψ〉A1A2B1B2C1C2⊗|η〉BB′.

(13)

Alice和Bob分别对自己的粒子(A、A′、A1)和(B、B′、B1)各作正交基三粒子量子联合测量,测量基为

(14)

Alice和Bob通过经典信道把测量的结果公布给对方.以下是Alice和Bob测量后的系统坍缩情况:

(15)

若Charlie同意双方通信则对粒子C1、C2做{|+〉,|-〉}基测量,并将结果公布给通信双方,测量后系统坍缩为64种情况之一.然后根据所有测量结果,Alice和Bob对粒子A2、B2做幺正变换见表2,其中i,j,k,l∈{+,-}.

表 2 三方测量结果以及对应幺正变换

假设Alice、Bob和Charlie测量结果为|φ+〉、|μ+〉、|+〉C1、|+〉C2,粒子A2、B2将坍缩为

(16)

Alice对粒子A2做σI变换,Bob对粒子B2做σI变换,得到新的形式分别为

(17)

Alice和Bob各自引进一个初态为|0〉的辅助粒子A3、B3,以A3、B3为目标比特,A2、B2为控制比特,进行控制非门操作,则粒子A2、A3量子态和粒子B2、B3量子态可表示成如下形式

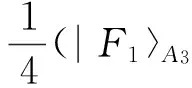
(18)

其中

|F1〉A3=x|0〉+y|1〉;

|E1〉A2=b0|0〉+b1|1〉,

|F2〉A3=x|0〉-y|1〉;

|E2〉A2=b0|0〉-b1|1〉.

(19)

(20)

其中

|F1〉B3=α|0〉+β|1〉;

|E1〉B2=a0|0〉+a1|1〉,

|F2〉B3=α|0〉-β|1〉;

|E2〉B2=a0|0〉-a1|1〉.

(21)

只要Alice对辅助粒子A3用|Fi〉A3(i=1,2)进行测量,就可对应获得量子态|Ei〉A3(i=1,2).|F1〉A3、|F2〉A3不是正交的,因而无法确定性的区分量子态,但是,可以通过局部测量方式以一定概率恢复原始量子信息.在这里采用POVM测量，首先构造如下测量算子:

P3=I-P1-P2,

(22)

其中

(23)

ε与x、y有关,其作用是保证P3是正算子.为了确定ε,这3个正算子可以写成矩阵的形式:

(24)

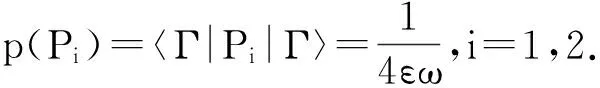
根据POVM的值,Alice就能够推断出辅助粒子A3的量子态,确定辅助粒子A3的量子态,随之确定粒子A2的量子态,进而选用适当的幺正变换就能重构A2量子态.假如Alice知道粒子A2量子态是|E1〉A2或|E2〉A2,则只需对粒子A2做σI或σZ变换.

同样地,Bob也用POVM测量方法对辅助粒子B3进行测量,同理可得3个正算子可以写成矩阵的形式:

(25)

根据POVM的值,Bob就能够推断出辅助粒子B3的量子态,如果Bob确定辅助粒子B3的量子态,粒子B2的量子态也就确定,Bob选用适当的幺正变换就能重构B2量子态.假如Bob知道粒子B2量子态是|E1〉B2或|E2〉B2,则只需对B2做σI或σZ变换.

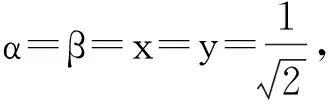
3 结语

本文提出三方参与的量子双向受控概率隐形传态方案,通过密享纠缠态实现Bell型纠缠态双向隐形传态.通信双方Alice和Bob既是发送者也是接收者,第三方Charlie控制和协助通信双方量子态的交换.通信开始后,Alice和Bob分别对自己拥有的个别粒子做测量,并公布结果,若控制方同意双方通信则对自己的粒子做测量,将自己所处的态公布.控制方的测量提高了方案的安全性.双方根据所有的测量结果对各自粒子做相应的幺正变换,引入辅助粒子完成投影测量、POVM测量及量子门操作,从而实现双向概率隐形传态.如果其中任何一方不合作,接收者都不能完美恢复出原始传送的未知量子纠缠态.有且仅当传输量子信道达到最大纠缠时,能够成功实现量子双向隐形传态.

[1] BENNETT C H, BRASSARD G, CREPEAU C, et al. Teleporting an unknown state via dual classical and Einstein-Podolsky-Rosen channels[J]. Phys Rev Lett,1993,70(13):1895-1899.

[2] 罗明星. 量子远程制备的理论研究进展[J]. 四川师范大学学报(自然科学版),2015,38(2):300-312.

[3] WANG J W, SHU L, MO Z W, et al. Controlled teleportation of a qudit state by partially entangled GHZ states[J]. Int J Theor Phys,2014,53(8):2867-2873.

[4] 吴柳雯,叶志清. 基于四粒子Ω纠缠态实现双向隐形传态[J]. 量子电子学报,2014,31(3):291-298.

[5] SANG M H. Bidirectional quantum teleportation by using five-qubit cluster state[J]. Int J Theor Phys,2016,55(3):1333-1335.

[6] HASSANPOUR S, HOUSHMAND M. Bidirectional teleportation of a pure EPR state by using GHZ states[J]. Quantum Inf Process,2016,15(2):905-912.

[7] ZHA X W, ZOU Z C, QI J X, et al. Bidirectional quantum controlled teleportation via five-qubit cluster state[J]. Int J Theor Phys,2013,52(6):1740-1744.

[8] 胡钰安,叶志清. 基于四粒子GHZ的可控量子双向隐形传态及安全性[J]. 光子学报,2014,43(8):0827001-0827005.

[9] 孙新梅,查新未. 基于六粒子最大纠缠态的双向控制隐形传态方案[J]. 光子学报,2013,42(9):1052-1056.

[10] YAN A. Bidirectional controlled teleportation via six-qubit cluster state[J]. Int J Theor Phys,2013,52(11):3870-3873.

[11] LI Y H , LI X L, SANG M H, et al. Bidirectional controlled quantum teleportation and secure direct communication using five-qubit entangled state[J]. Quantum Inf Process,2013,12(12):3835-3844.

[12] SHUKLA C, BANERJEE A, PATHAK A. Bidirectional controlled teleportation by using 5-qubit states:a generalized view[J]. Int J Theor Phys,2013,52(10):3790-3796.

[13] DUAN Y J , ZHA X W, SUN X M, et al. Bidirectional quantum controlled teleportation via a maximally seven-qubit entangled state[J]. Int J Theor Phys,2014,53(8):2697-2707.

[14] LI Y H, NIE L P. Bidirectional controlled teleportation by using a five-Qubit composite GHZ-Bell state[J]. Int J Theor Phys,2013,52(5):1630-1634.

[15] CHEN Y. Bidirectional quantum controlled teleportation by using a genuine six-qubit entangled state[J]. Int J Theor Phys,2015,54(1):269-272.

[16] SANG M H. Bidirectional quantum controlled teleportation by using a seven-qubit entangled state[J]. Int J Theor Phys,2016,55(1):380-383.

2010 MSC：35K05

(编辑 郑月蓉)

Bidirectional Controlled Probabilistic Teleportation of Bell-type Entangled State

WANG Xiaoyu, MO Zhiwen

(College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan)

A scheme of bidirectional controlled teleportation of Bell-type State is proposed with non-maximally entangled state as quantum channel. Two sides of communication (Alice and Bob)and the controller (Charlie) secretly share entangled state in advance to construct quantum channel. After communication, Alice and Bob perform quantum projection measurement on their own qubits respectively, and announce the measurement results via classical channel. If Charlie agrees to intercommunication, he should measure his qubits and announce the results via classical channel. Then according to the all measurement results, Alice and Bob can make appropriate unitary transformations. Both Alice and Bob introduce an auxiliary qubit, and perform the projective measurement or positive-operation valued measurement respectively. At last they introduce an auxiliary qubit again to recover the teleported states.

entangled state; unitary transformation; bidirectional quantum teleportation; projective measurement

2016-03-04

教育部博士点专项科研基金(20135134110003)

O59

A

1001-8395(2016)06-0815-06

10.3969/j.issn.1001-8395.2016.06.006

*通信作者简介：莫智文(1963—),男,教授,主要从事人工智能、模糊语言、粗糙集、量子信息处理的研究,E-mail:mozhiwen@263.net