给定不确定结果的量子比特的量子态区分*
张 刚,张文海
(1.皖西学院机械与电子工程学院,安徽 六安 237012; 2.淮南师范学院物理系,安徽 淮南 232038)
给定不确定结果的量子比特的量子态区分*
张 刚1,张文海2
(1.皖西学院机械与电子工程学院,安徽 六安 237012; 2.淮南师范学院物理系,安徽 淮南 232038)
给出更简单的利用辅助测量比特和系统的幺正演化的方法用于在给定不确定结果时的量子比特的两个量子态区分。方案涵盖了当不确定结果的概率为零时的最小错误区分,以及当不确定结果的概率为某些数值时的最优确定性区分。文中给出最大全局正确概率和给定不确定概率关系的解析式。利用辅助测量比特,对被测的非正交量子态初态系统实施幺正演化,对输出态进行正交测量,就可以完成非正交态的量子态区分。方案提供了一种对于两个非正交量子态的正定算符值测量的物理实现方法。
量子态区分;最小错误区分;确定性区分
量子力学指出:正交量子态可以被精确地测量(区分),而非正交量子态则不能。在量子密钥分配(Quantum key distribution,QKD)中[1-2],通信双方利用非正交量子态进行量子通信。量子态被用于编码成量子密钥,通信双方通过测量非正交量子态而使接收方获得量子密钥。因此,量子态区分(Quantum state discrimination,QSD)就成为量子信息中一个基本研究方向[3]。目前,大量的研究工作关注于这个方向,并且量子态区分理论研究发展迅速。
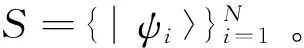
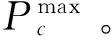
1 两个量子态的POVM
我们首先介绍文献[23]中利用POVM对两个量子态进行区分。特殊的输入量子态形式为
|ψ1〉=cosθ1|1〉+sinθ1|2〉,
|ψ2〉=cosθ2|1〉+sinθ2|2〉
(1)
它们的内积为
s=〈ψ1|ψ2〉=cos(θ1-θ2)=cosθ∈(-1,1)
(2)
一般而言,任意两个量子态的内积是复数。我们将在下一节里设定量子态的内积为复数,所得到的结果能对任意两个量子态都适用。对于两个量子态的先验概率ηi(i=1,2),满足关系η1+η2=1, 文献[23]设定在POVM元的集合中,三个测量元表示为Π={Π0,Π1,Π2},并满足Π0+Π1+Π2=I(I是单位算符,该式表示为量子测量的完备性), 其中算符Π1(2)表示可以对输入量子态ρ1(2)=|ψ1(2)〉〈ψ1(2)|的判定, 而算符Π0则对应为不确定结果。定义测量量子态|ψ1〉和|ψ2〉的正确概率为p11=tr(ρ1Π1)和p22=tr(ρ2Π2),这意味着当算符Πi(i=1,2)出现时,可以正确概率pii判断输入态是ρi。测量错误的概率为p12=tr(ρ2Π1)和p21=tr(ρ1Π2),这就是说,当算符Πi(i=1,2)出现时,会以错误的概率pij(j=1,2;i≠j)认为输入态是|ψj〉。不确定概率为q1=tr(ρ1Π0)和q2=tr(ρ2Π0),这意味着,当算符Π0出现时,不能判断输入态。显然,在不出现错误判断pij=0,以及也不存在不确定概率qi=0时,就可以确定性地判断输入态。但是,这是不可能的,因为非正交量子态是不可能确定性地被判断,这是量子力学中的基本原理(量子态叠加原理)。当然,正交量子态是可以被确定性地测量。因此,经典的测量方案有两种:① 当不确定概率qi=0时,测量就会出错,有pii≠0和pij≠0,这就是MD;② 如果希望测量不出错pij=0(此时算符Πi的出现就可以确定性地判断输入态为|ψi〉),就必须有qi≠0,这就是UD。
结合输入态的先验概率η1和η2=1-η1,传统上规定全局正确概率Pc,全局错误概率Pe以及不确定概率Q的定义如下[23]:
Pc=tr(η1ρ1Π1)+tr(η2ρ2Π2)=η1p11+η2p22,
Pe=tr(η1ρ1Π2)+tr(η2ρ2Π1)=η1p21+η2p12,
Q=tr(η1ρ1Π0)+tr(η2ρ2Π0)=η1q1+η2q2
(3)
显然,(3)式给出概率关系Pc+Pe+Q=1。对于给定的不确定概率Q,文献[23]是求解全局正确概率Pc最大值(等价于求解全局错误概率Pe的最小值)。对于特殊的输入态(1),文献[23]定义
(4)

(5)

(6)
对(6)式求逆可得Pc/e(Q),但是文献[23]并没有分析,原因是Pc/e(Q)是多值函数,得不出明显的含义。在本文中,我们得出了(6)式具体的反函数。
本节介绍文献[23]的结果。从其内容可以看出,文献[23]选择的是特殊输入态(两个量子态的内积为实数),而一般的量子态的内积是复数。其次,在角度为特殊值φ=π/4时,(5)式给出最大全局正确概率和给定不确定概率的具体解析式;而在取任意值时,(6)式给不出明确的关系。最后,文献[23]利用POVM得出相应的概率,但是,POVM本身不能直接在物理上实现,需要将POVM转化为物理上可以实现的测量。在下一节中,将选取一般的量子态作为输入态,并给出物理上可以直接实现的测量方案,最后得出最大全局正确概率和给定不确定概率的具体解析式。
3 两个量子态区分
选取两个非正交量子态|ψ1〉和|ψ2〉, 它们的内积一般为〈ψ1|ψ2〉复数, 可以不失一般性地定义为
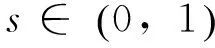
(7)
利用文献 [24-25]的方法, 可以首先将一个幺正变换作用在输入态上,然后对输出态进行正交测量。对于MD,幺正变换定义为
(8)
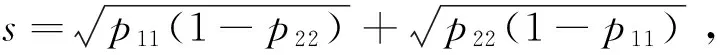
(9)
Helstrom界限表示为[4]
(10)
对于UD,引入辅助测量比特|1〉a,定义幺正变换为
(11)
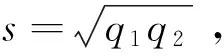
(12)
最优成功概率为
(13)
这就是JS极限[8]。当等概率输入时,(13)式退化为IDP极限[5-7]。


(14)

|ψ2〉→eiφ|2〉|2〉a
(15)
这种情况下量子态|ψ2〉就不能被判断,最小不确定概率为Q=η1s2+η2。上述UD的结果已由POVM方法得出[23,26],我们给出的幺正变换,可以直接在物理上实现MD和UD。
上述的方法可以直接推广到文献[23]的情况,相应的幺正变换定义为
(16)
(16)式给出概率系数的归一化条件和两个量子态的内积:
p11+p21+q1=1,p12+p22+q2=1
(17-1)
(17-2)
将(17-1)代入(17-2)可以得到
(18)

(19)
最大全局正确概率为
(20)
将a,b和c的数值代入(20)式中,可以得到
(21)


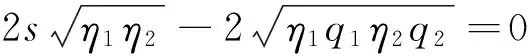
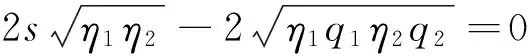
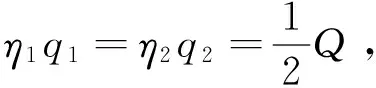
(Q0≥Q≥0)
(22)
这个解析式的形式和(5)式相同,并且对任意两个非正交量子态都适用,是最优QSD。
(23)

由于POVM定义测量算符可以是非正交的,而非正交测量在物理上是不可以实现的,所以对非正交的POVM算符不可能直接在物理上实现。我们利用辅助测量比特,对初态系统实施幺正演化,将POVM测量算符转化为对输出态的正交测量。幺正演化和正交测量在物理上是可以实现的,因此,方案(16)式为实现量子态区分的POVM提供了一种物理实现的具体方法。
3 结 论
本文得出了在给定不确定概率情况下,两个非正交量子态区分的普遍式,具体表示为最大全局正确概率是给定不确定概率的函数解析式。提出的方案适合任意区间的先验概率。同时,方案给出的幺正变换为实现量子态区分的POVM提供了物理实现的具体方法。
[1]GISINN,RIBORDYG,TITTELW,etal.Quantumcryptography[J].RevModPhys,2002, 74(1): 145-197.
[2]SCARANIV,BECHMANN-PH,CERFN,etal.Thesecurityofpracticalquantumkeydistribution[J].RevModPhys, 2009, 81(3): 1301 -1350.
[3]BARNETTSM,CROKES.Quantumstatediscrimination[J].AdvOptPhoton, 2009, 1(2): 238-437.
[4]HELSTROMCW.Quantumdetectionandestimationtheory[M].NewYork:AcademicPress,1976.
[5]IVANOVICID.Howtodifferentiatebetweennon-orthogonalstates[J].PhysLettA, 1987, 123(6): 257-259.
[6]DIEKSD.Overlapanddistinguishabilityofquantumstates[J].PhysLettA, 1988 126(5): 303-306.
[7]PERESA.Howtodifferentiatebetweennon-orthogonalstates[J].PhysLettA, 1988,128 (1): 19.
[8]JAEGERG,SHIMONYA.Optimaldistinctionbetweentwonon-orthogonalquantumstates[J].PhysLettA, 1995, 197(2): 83-87.
[9]BARNETTSM.Minimum-errordiscriminationbetweenmultiplysymmetricstates[J].PhysRevA, 2001, 64(3): 030303(R).
[10]HERZOGU,BERGOUJA.Minimum-errordiscriminationbetweensubsetsoflinearlydependentquantumstates[J].PhysRevA, 2002, 65(5): 050305(R) .
[11]CHOUCL.Minimum-errordiscriminationamongmirror-symmetricmixedquantumstates[J].PhysRevA, 2004, 70(6): 062316 .
[12]MOCHONC.Familyofgeneralized“prettygood”measurementsandtheminimal-errorpure-statediscriminationproblemsforwhichtheyareoptimal[J].PhysRevA, 2006, 73(3): 032328 .
[13]QIUD.Minimum-errordiscriminationbetweenmixedquantumstates[J].PhysRevA, 2008, 77(1): 012328.
[14]TYSONJ.ErrorratesofBelavkinweightedquantummeasurementsandaconversetoHolevo’sasymptoticoptimalitytheorem[J].PhysRevA, 2009, 79(3): 032343.
[15]ASSALINIA,CARIOLAROG,PierobonG.Efficientoptimalminimumerrordiscriminationofsymmetricquantumstates[J].PhysRevA, 2010, 81(1): 012315.
[16] BAE J, HWANG W Y. Minimum-error discrimination of qubit states: Methods, solutions, and properties [J]. Phys Rev A, 2013, 87(1): 012334.
[17] PERES A, TERNO D. Optimal distinction between non-orthogonal quantum states [J]. J Phys A, 1998, 31(34): 7105.
[18] CHEFLES A. Unambiguous discrimination between linearly independent quantum states[J]. Phys Lett A, 1998, 239(6): 339-347.
[19] SUN Y, HILLERY M, BERGOU J A. Optimum unambiguous discrimination between linearly independent nonorthogonal quantum states and its optical realization [J]. Phys Rev A , 2001, 64 (2): 022311.
[20] JAFARIZADEH M A, REZAEI M, KARIMI N, et al. Optimal unambiguous discrimination of quantum states [J]. Phys Rev A, 2008, 77(4): 042314.
[21] SAMSONOV B F. Optimal positive-operator-valued measures for unambiguous state discrimination [J]. Phys Rev A, 2009, 79(4): 042312.
[22] BERGOU J A, FUTSCHI U k, FELDMAN E. Optimal unambiguous discrimination of pure quantum states [J]. Phys Rev Lett, 2012,108(25): 250502 .
[23] BAGAN E, MUOZ-T R, OLIVARES-R G A, et al. Optimal discrimination of quantum states with a fixed rate of inconclusive outcomes [J]. Phys Rev A, 2012, 86(4): 040303 (R) .
[24] ZHOU X F, LIN Q, ZHANG Y S, et al. Physical accessible transformations on a finite number of quantum states [J]. Phys Rev A, 2007, 75(1): 012321.
[25] ZHO X F, ZHANG Y S, GUO G C. Unambiguous discrimination of mixed states: A description based on system-ancilla coupling [J]. Phys Rev A , 2007, 75 (5): 052314.
[26] BERGOU J A. Discrimination of quantum states [J]. Journal of Modern Optics, 2010, 57(3): 160.
By exploiting an ancillary measured qubite and a system unitary evolution, a simpler method for state discrimination of qubits with a fixed inconclusive answer is given. The strategy includes the minimal error discrimination is zero as the probability of an inconclusive answer and the optimal unambiguous discrimination is some value as the probability of an inconclusive answer.The analytical solution was derived between the maximal total correct probability and the fixed inconclusive probability. By using an ancillary measured qubite, a unitary transformation acts on the whole initial system and the orthogonal measures on the output states can reach quantum state discrimination of two nonorthogonal states. The scheme itself provides an implementation of a positive operator-valued measure of two nonorthogonal quantum states.
quantum state discrimination; minimum-error discrimination; unambiguous discrimination
2014-07-20
安徽省自然科学基金资助项目(1408085MA20);安徽省教育厅自然科学基金资助项目(KJ2010A323 )
张刚(1975年生),男;研究方向:量子信息与量子计算;E-mail:zhanggang@wxc.edu.cn
10.1347/j.cnki.acta.snus.2015.01.011
O
A
0529-6579(2015)01-0052-06
State Discrimination of Qubits with a Fixed Inconclusive Answer
ZHANGGang1,ZHANGWenhai2
(1.School of Mechanical and Electronic Engineering, West Anhui University, Lu’an 237012,China; 2.Department of Physics, Huainan Normal University, Huainan 232038,China)

