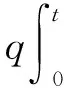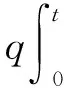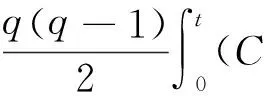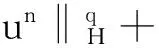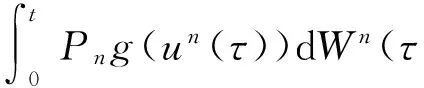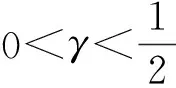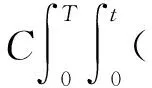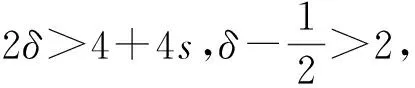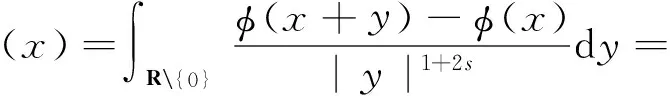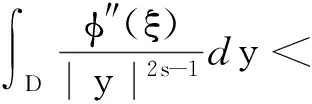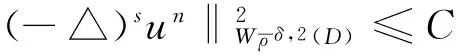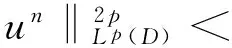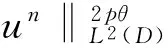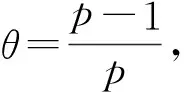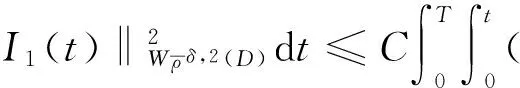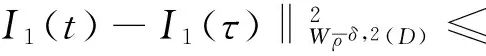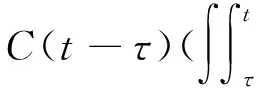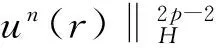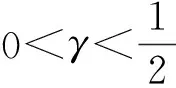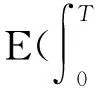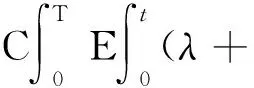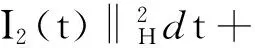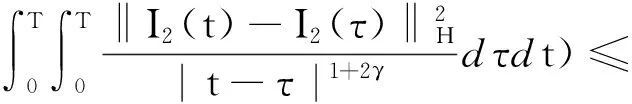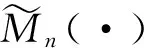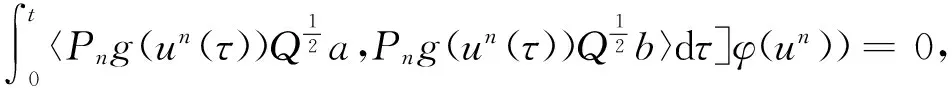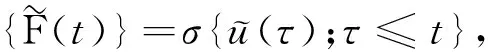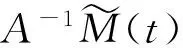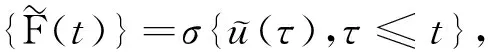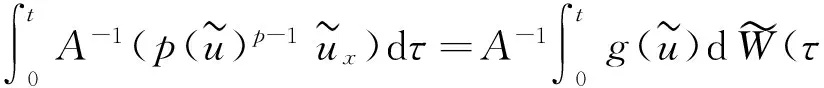有界区间上的随机广义非局部Burgers方程鞅解的存在性
何 兴, 陈光淦, 杨 欢
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
有界区间上的随机广义非局部Burgers方程鞅解的存在性
何 兴, 陈光淦*, 杨 欢
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
研究有界区域上随机广义非局部Burgers方程.通过在适当的加权空间上考虑,克服了有界区域上非局部Laplace算子带来的困难.运用一系列精致估计获得了系统的某些有界性.利用胎紧代替噪声给系统带来的通常意义下的紧性问题,最终获得系统鞅解的存在性.
随机广义Burgers方程; 有界区域; 非局部Laplace算子; 鞅解
Burgers方程首先由H. Bateman[1]给出,并把这个方程作为湍流模型研究,成为流体力学中一类非常重要和基本的非线性偏微分方程,并被广泛地应用于空气动力学、湍流、热传导、交通流、地下水污染等众多领域[2-4].
本文考虑如下随机广义非局部Burgers方程
(1)
其中D=(-1,1),Dc=RD,非线性项幂指数p满足2 (-△)su(x)= 其中Cs是与s有关的常数. 对于方程(1),当g(u)=0时为确定系统,当s=1,p=2,即为经典的Burgers方程[1];当s=1,p>2,即为广义的Burgers方程[5];当0 本文研究有界区间上的随机广义非局部Burgers方程(1)的鞅解.由于在有界区间上通常的Laplace算子和非局部Laplace算子有明显不同[9],通常的分数阶Sobolev空间不再适用,因此引入加权的Sobolev空间,再利用胎紧代替噪声给系统带来的通常意义下的紧性不成立,最终获得该系统鞅解的存在性. 引理 1.1[10]设D⊂R,1≤p1 如果f∈Lp1(D)∩Lp3(D),则f∈Lp2(D),进一步有 引理1.2[11]设B0、B、B1均为Banach空间,且B0和B1是自反的,B0⊂B⊂B1,同时B0紧嵌入到B,γ∈(0,1),X=L2(0,T;B0)∩Wγ,2(0,T;B1),则X紧嵌入到L2(0,T;B). 定义 1.1[12]设s∈(0,1),D⊂R,定义分数阶Sobolev空间 Ws,2(D)= 其范数为 ‖u‖Ws,2(D)= 这里 被称为u的半范数. 本文考虑D=(-1,1)⊂R,由文献[12]有 ). 再根据文献[13],设ν(x,y),β(x,y):R×R→Rk,其中β满足β(x,y)=-β(y,x),且 y.x))·β(x,y)dy. 显然D(ν):R→R.给定映射u(x):R→R,D表示D的伴随算子,则 显然D(u):R×R→Rk.用Θ(x,y)=Θ(y,x)表示二阶张量,且满足Θ=ΘT,那么有 D(Θ·Du)(x)= 其中x∈R,D(Θ·Du):R→R.当Θ为单位矩阵,同时β满足2|则 D(Θ·D 其中D从而有 D(Θ·Du)(x). 〈(-△)su,u〉L2(D)=〈D(Du)(x),u(x)〉L2(D)= 〈D(Du)(x),u(x)〉L2(R)= (5) 上述计算用到了u|Dc=0.由(5)知经典的分数阶Sobolev空间Ws,2(D)在这里不适用,因为不能保证 如果定义 则 在RD}. 其范数为 由(5)式知 ‖Du‖L2(D)=‖ (6) 结合(5)和(6)式可得 本文记 则有V⊆H=H⊆V⊆V1. 定义 1.2 如果存在一个随机基(Ω,F,{Ft},P),一个在空间U上的维纳过程W以及一个逐渐可测过程u:Ω×[0,T]×D→H,在几乎必然的意义下,函数 u∈L∞(0,T;H)∩L2(0,T;V)∩C([0,T];V1), 且使得对任意的t∈[0,T],υ∈V有 则称方程(1)存在一个鞅解,并称满足上述的序列(Ω,F,P,{Ft},W,u)为方程(1)的鞅解. 设W(t)是一个完备概率空间(Ω,F,P)上的维纳过程,且在可分的Hilbert空间U上取值.算子Q是定义在U上的非负对称算子,满足TrQ<+∞,则在U上存在一个完备的标准正交集{ei}i≥1和非负的有界实值序列λi,使得Qei=λiei且 进一步假设 (A)g:H→L2(U,H)是连续的,且满足 其中u,v∈H,参数C、λ为正实数. 证明 第一步,有限维近似. 假设{η1,η2....}⊂V是空间H中的一组标准正交基.令Hn:=span{η1,η2,…,ηn},定义线性算子Pn:V→Hn, 显然Pn|H是H到Hn的正交投影,且对∀u∈V,υ∈Hn可得 V〈Pn(-△)su,υ〉V=〈Pn(-△)su,υ〉H, 其中V〈·,·〉V表示V和它的对偶空间V的对偶积.取U上的一组标准正交基{e1,e2,…},且 由于在有限维空间上的随机微分方程(7)满足局部Lipschitz和线性增长条件,则方程(7)有唯一强解un(t)∈L2(Ω;C([0,T];Hn)). 第二步,先验估计. 注意到 〈(-△)su,u〉L2(D)=‖ 再利用It公式和假设(A)可得 于是由Gronwall不等式可得 (8) 其中C1、C2是正常数.同理q≥2时有 再利用Burkholder-Davis-Gundy不等,Young不等式以及Gronwall不等式可得 (9) 其中C与n无关.由(8)式有 {un}n∈N在L2(Ω,L2(0,T;V)) un(t)=Pnu0+ 记 ‖u‖L2(D)‖(-△)sφ(x)‖L2(D), 则可得‖(-△)sφ(x)‖L2(D)≤C,进一步有 ‖ ‖ 因为2δ>4+4s,由嵌入不等式得 ‖φx‖L∞(D)≤C‖φ 所以 令2 因此第一部分 (10) 下面来看第二部分 类似计算可得 (11) (12) 下面来证I2(t)在L2(Ω,Wγ,2(0,T;H))上一致有界.同理先来看第一部分 (13) 再来看第二部分 (14) 由(13)和(14)式可得 (15) 上一致有界. 记 Mn(t):=un(t)-Pnu0+ 则Mn(·)是一个鞅,其二阶变差为 〈〈Mn(t)〉〉= 则由E([Mn(t)-Mn(τ)]φ(un(·)))=0,从而 且对∀a,b∈H,有 相应的滤子为 二阶变差为 二阶变差为 因此对任意的t∈[0,T],υ∈V有 [1] BATEMAN H. Some recent researches on the motion of fluids[J]. Monthly Weather Rev,1915,43(4):163-170. [2] CATUOGNO P, OLIVERA C. Strong solution of the stochastic Burgers equation[J]. Applicable Analysis,2014,93(3):646-652. [3] TIAN C. New strong symmetry, symmetries and lie algebra of burgers equation[J]. Scientia Sinica,1988,31(2):141-151. [4] 胡劲松,王玉兰,郑茂波. Rosenau-Burgers方程的一个新的差分格式[J]. 四川师范大学学报(自然科学版),2010,33(4):455-457. [5] VANEEVA O O, SOPHOCLEOUS C, LEACH P G L. Lie symmetries of generalized Burgers equations: application to boundary-value problems[J]. J Engineering Math,2015,91(1):165-176. [6] BILER P, FUNAKI T, WOYCZYNSKI W A. Fractal Burgers equation[J]. J Diff Eqns,1998,148(1):9-46. [7] BERTINI L, CANCRINI N, JONA-LASINIO G. The stochastic Burgers equation[J]. Commun Math Phys,1994,165(2):211-232. [8] HAIRER M, VOSS J. Approximations to the Stochastic Burgers Equation[J]. J Nonlinear Sci,2011,21(6):879-920. [9] DU Q, GUNZBURGER M, LEHOUCQ R B, et al. Analysis and approximation of nonlocal diffusion problems with volume constraints[J]. SIAM Rev,2012,54(4):667-696. [10] 陈国旺. 索伯列夫空间导论[M]. 北京:科学出版社,2013. [11] FLANDOLI F, GATAREK D. Maitingale and stationary solutions for stochastic Navier-Stokes equations[J]. Probab Theory Realt Fields,1995,102(3):367-391. [12] NEZZA E D, PALATUCCI G, VALDINOCI E.Hitchhiker’s guide to the fractional Sobolev spaces[J]. Bull Sci Math,2012,136(5):521-573. [13] DU Q, GUNZBURGER M, LEHOUCQ R B, et al. A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws[J]. Math Models Methods Appl Sci,2013,23(3):493-540. [14] DA PRATO G, ZABCZYK J. Stochastic Equations in Infinite Dimensions[M]. Cambridge:Cambridge University Press,1992. [15] BRZEZNIAK Z, MOTYL E. Existence of a martingale solution of the stochastic Navier-Stokes equations in unbounded 2D and 3D domains[J]. J Diff Eqns,2013,254(4):1627-1685. 2010 MSC:60H15; 60G46; 35Q53 (编辑 陶志宁) The Existence of Martingale Solution for a Stochastic Generalized Nonlocal Burgers Equation on Bounded Intervals HE Xing, CHEN Guanggan, YANG Huan (College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan) This paper is concerned with the stochastic generalized nonlocal Burgers equation on bounded intervals. Introducing a weighted sobolev space, it overcomes the difficulties which are caused by the nonlocal Laplacian operator on bounded domains. By using a series of precise estimates, the boundedness of the system is established. Using the tightness to solve the general compact problem which is caused by noise, it finally obtains the existence of martingale solutions for the system. Stochastic generalized burgers equation; bounded intervals; Nonlocal laplacian operator; Martingale solution 2015-11-08 国家自然科学基金(11571245和11401409)及四川省教育厅重点科研项目(15ZA0031) O175.2 A 1001-8395(2016)06-0809-06 10.3969/j.issn.1001-8395.2016.06.005 *通信作者简介:陈光淦(1978—),男,教授,主要从事随机偏微分方程的研究,E-mail:chenguanggan@hotmail.com1 预备知识




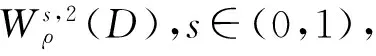

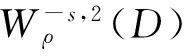
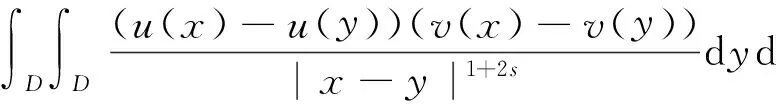
2 鞅解的存在性