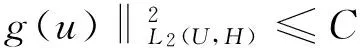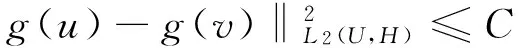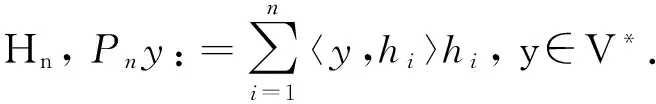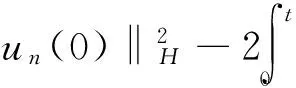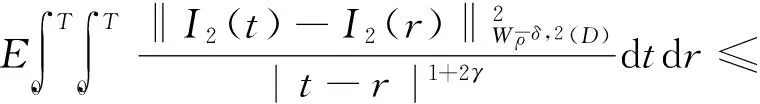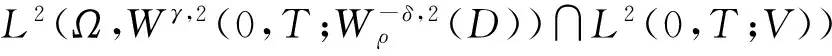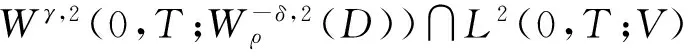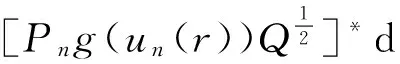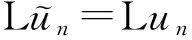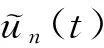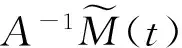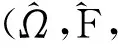有界区间上随机分数阶反应扩散方程鞅解的存在性
杨 欢, 陈光淦, 何 兴
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
有界区间上随机分数阶反应扩散方程鞅解的存在性
杨 欢, 陈光淦*, 何 兴
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
有界区间上随机分数阶反应扩散方程在分数阶非相对量子力学中起到很重要的作用.由于噪声和有界区间上分数阶Laplace算子的扰动和影响,使随机分数阶反应扩散方程的研究变得复杂.通过引入一个适当的加权函数来构造加权空间,运用算子理论来克服有界区间上的分数阶Laplace算子带来的困难.运用Prokhorov定理和Skorokhod嵌入定理来解决噪声带给系统的通常紧性不成立的收敛问题.利用It公式和一系列精致的不等式技巧,以及Galerkin方法,最终获得系统鞅解的存在性.
有界区间上分数阶Laplace算子; 白噪声; 反应扩散方程; 鞅解
有界区域上的分数阶反应扩散方程是常扩散方程的一种拓展,它源于反常扩散模型,用于描述具有分形结构的多孔介质中的反常扩散现象,在物理、财经、水文学、以及工程学、材料科学等方面,都有广泛应用[1-6].
本文考虑如下随机分数阶反应扩散方程
(1)
这里,有界区间D=(-1,1)⊂R1,Dc=R1D,W(t)是一个Wiener过程.分数阶Laplace算子(-Δ)s定义如下
0 (2) 其中Cs是依赖于s的常数.有界区域上的分数阶Laplace算子(-Δ)s与正常的Laplace算子有很大的不同[7].因此,对于有界区域上的分数阶Laplace算子驱动的发展方程,受到了许多数学家的关注[7-9]. 本文关心有界区域上分数阶Laplace算子驱动的随机分数阶反应扩散方程.分析了分数阶Laplace算子和白噪声的特征.为了克服有界区域上分数阶Laplace算子带来的困难,引入一个新的加权函数,来构造加权Sobolev空间,进而再在这个空间上对方程进行研究.由于噪声的扰动,系统(1)通常意义下的紧性不再成立,运用胎紧来代替.运用Prokhorov定理和Skorokhod嵌入定理来解决序列的收敛问题,最终获得系统鞅解的存在性. 设s∈(0,1),D⊂R1且为有界区域,定义如下: Ws,2(D):={u∈L2(D): 其中,‖u‖Ws,2(D)和[u]Ws,2(D)分别为经典的分数阶Sobolev空间Ws,2(D)的范数和半范数[10]. 引理 1.1[10]设0 ‖u‖Ws,2(D)≤C‖u‖W1,2(D), W1,2(D)⊆Ws,2(D). 引理 1.3[11]设B0⊂B⊂B1,均为Banach空间,B0与B1是自反的,B0紧嵌入到B.设γ∈(0,1),X=L2(0,T;B0)∩Wγ,2(0,T;B1),那么X紧嵌入到L2(0,T;B). 根据文献[8-9]有 x∈R1, J*(u)(x,y)=-(u(y)-u(x))β(x,y), x,y∈R1, β(x,y)(Θ(x,y)β(x,y))dy, 其中,J是非局部散度算子,J*为J的伴随算子,V(x,y),β(x,y):R1×R1→Rk,β是反对称的,u(x):R1→R1,Θ(x,y)=Θ(y,x)为一个二阶张量满足Θ=ΘT. (3) 设D⊂R1是一个开的有界区域,由文献[10]及(2)式得 (-Δ)su(x)=J(Θ·J*u)(x)=J(J*u)(x). 〈(-Δ)su,u〉L2(D)=〈J*u(x),J*u(x)〉= (5) 由x∈D=(-1,1),知ρ(x)有严格的正下界和上界,因此,加权分数阶Sobolev空间范数定义为 从而 (6) 本文记 假设(H1):f(u)满足 k2|u|p-α2|u|2≤f(u)u≤ k1|u|p+α1|u|2, 2 其中k1、k2、α1、α2均为正常数. 假设(H2):g:H→L2(U,H)是连续的,且满足 ∀u,v∈H, 其中C和λ为正常数.在本文中,假定C均为正常数,但是出现的C有所不同. u∈L∞(0,T;H)∩L2(0,T;V)∩C([0,T];V1), 且使得对任意的t∈[0,T],v∈V有 (7) 则称(Ω,F,,{Ft}t≥0,W,u)是方程(1)的鞅解. 定理 2.1 假定s∈(1/2,1),初值u0满足F0可测,且u0∈L2(Ω,H).设(H1)和(H2)成立,则方程(1)存在一个鞅解. 任给n∈N,在有限维空间Hn上考虑以下随机方程 (8) 由于在有限维空间上的随机微分方程(8)满足局部Lipschitz条件和线性增长,方程(8)有唯一强解un(t)∈L2(Ω;C([0,T];Hn))[12],满足 (9) 由假设(H1),于是得 再利用Gronwall不等式,可得 (10) 由(10)式,知方程(8)的解{un}n∈N在空间L2(Ω,L2(0,T;V))上一致有界. -Pn(-Δ)sun(r)-Pnf(un(r))〉dr+ 于是,由Burkholder-Davis-Gundy不等式和Young不等式得 由假设(H1),从而 又由Gronwall不等式得 (11) 以上所有的C不依赖于n. 根据(9)式,令 (-Δ)sφ(x)= C‖un‖H. (12) 故由(10)、(11)和(12)式,以及内插不等式和假设(H1)得 2k1α1‖ (13) 再由Burkholder-Davis-Gundy不等式及假设(H2)得 (14) 定义 Mn(t)=un(t)-Pnu0+ 由(9)式,于是Mn(·)是一个鞅,其二阶变差为 E([Mn(t)-Mn(r)]φ(un(·)))=0, 进一步 E([〈Mn(t),a〉〈Mn(t),b〉- φ(un(·)))=0, (15) (16) r. (17) 从而对任意的t∈[0,T],v∈V有 [1] ZHUANG P, LIU F, ANH V, et al. New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equation[J]. SIAM Journal on Numerical Analysis,2008,46(2):1079-1095. [2] LI X, XU M, JIANG X. Homotopy perturbation method to time-fractional diffusion equation with a moving boundary[J]. Applied Mathematics and Computation,2009,208(2):434-439. [3] 孙峪怀,杨少华,王佼,等. 非线性Chaffee-Infante反应扩散方程的新精确解[J]. 四川师范大学学报(自然科学版),2012,35(3):293-296. [4] 许永红,陈贤峰,韩祥临,等. 具有双参数的非局部反应扩散方程非线性奇摄动问题[J]. 陕西师范大学学报(自然科学版),2015,43(1):8-12. [5] REN C, XU X. Local stability for an inverse coefficient problem of a fractional diffusion equation[J]. Chin Ann Math,2014,B35(3):429-446. [6] 黄锐,尹景学. 全空间RN中反应扩散方程的非平面行波解[J]. 华南师范大学学报(自然科学版),2013,45(1):1-9. [7] KWASNICKI M. Eigenvalues of fractional Laplace operator in the interval[J]. J Funct Anal,2012,262(5):2379-2402. [8] DU Q, GUNZBURGER M, LEHOUCQ R B, et al. Analysis and approximation of nonlocal diffusion problems with volume constraints[J]. SIAM Rev,2012,54(4):667-696. [9] DU Q, GUNZBURGER M, LEHOUCQ R B, et al. A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws[J]. Math Models Methods Appl Sci,2013,23(3):493-540. [10] NEZZA E D, PALATUCCI G, VALDINOCI E. Hitchhiker’s guide to the fractional Sobolev spaces[J]. Bull Sci Math,2012,136(5):521-573. [11] FLANDOLI F, GATAREK D. Martingale and stationary solutions for stochastic Navier-Stokes equations[J]. Probab Theory Realt,1995,102(3):367-391. [12] PREVOT C, ROCKNER M. A Concise Course on Stochastic Partial Differential Equations[M]. Berlin:Springer-Verlag,2007. [13] JAKUBOWSKI A. The almost sure Skorokhod representation for subsequences in nonmetric spaces[J]. Translation in Theory Probab Appl,1998,42(1):167-175. [14] DA PRATO G, ZABCZYK J. Stochastic equations in infinite dimensions[C]//Encyclopedia of Mathematics and its Applications, 44. Cambridge:Cambridge University Press,1992. [15] BRZEZNIAK Z, MOTYL E. Existence of a martingale solution of the stochastic Navier-Stokes equations in unbounded 2D and 3D domians[J]. J Differential Equations,2013,254(4):1627-1685. 2010 MSC:35K05; 60H15; 60G46 (编辑 周 俊) The Existence of Martingale Solution of the Stochastic FractionalReaction-diffusion Equation on Bounded Intervals YANG Huan, CHEN Guanggan, HE Xing (College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan) This paper studies the stochastic fractional reaction-diffusion equation on bounded intervals, which plays a very important role in fractional nonrelativistic quantum mechanics. Due to interacting and disturbing of the fractional Laplacian operator on a bounded interval with white noise, the stochastic fractional reaction-diffusion equation is too complicated to be understood. By introducing a suitable weight function to construct the weighted space, we apply the operator theory to overcome the difficulties caused by the fractional Laplacian operator on bounded intervals. We apply Prokhorov theorem and Skorokhod embedding theorem to solve the convergence problem instead of losing the common compactness of the system caused by the white noise. On the basis of Itformula, a series of exquisite inequalities and Galerkin approximation, we finally establish the existence of the martingale solution of the stochastic fractional reaction-diffusion equation on bounded intervals. fractional Laplacian operator on bounded intervals; white noise; reaction-diffusion equation; martingale solution 2015-11-08 国家自然科学基金(11571245和11401409)和四川省教育厅重点科研项目(15ZA0031) O175.2 A 1001-8395(2016)06-0794-07 10.3969/j.issn.1001-8395.2016.06.003 *通信作者简介:陈光淦(1978—),男,教授,主要从事随机偏微分方程的研究,E-mail:chenguanggan@hotmail.com1 预备引理

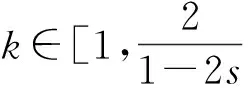
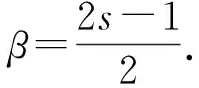
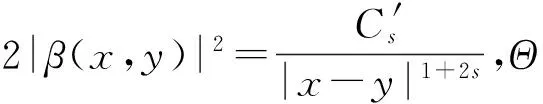
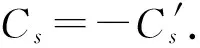



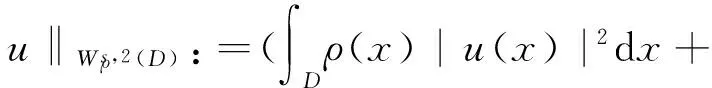
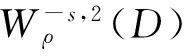






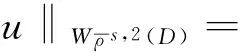

2 鞅解的存在性