集值拟变分不等式的间隙函数和误差界

杨 博, 夏福全

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

集值拟变分不等式的间隙函数和误差界

杨 博, 夏福全*

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

首先研究集值拟变分不等式的间隙函数,然后利用该间隙函数建立集值拟变分不等式与优化问题间的等价关系,利用这一等价关系讨论集值拟变分不等式的误差界问题,这些结论是文献(Fan H J, Wang G X. Comput Appl Math,2010,233:2956-2965和Tang G J, Huang N J. Taiwanese J Math,2013,17:1267-1286.)中相关结果的推广.

集值拟变分不等式; 间隙函数; 误差界

变分不等式在最优控制、非线性规划、物理学、经济学、工程学等诸多领域都有广泛的应用,许多学者在变分不等式问题上作了深入研究,获得了丰富结果[1-12].拟变分不等式问题出现相对较晚,但经过几十年的发展,拟变分不等式的研究已较深入,并应用在力学及经济学等问题中.

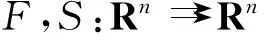
〈u*,y-x*〉≥0, ∀y∈S(x*).

(1)

本文记集值映射S的不动点集、图像、有效域分别为FP(S){x∈Rn|x∈S(x)}、Graph(S){(x,y)|x∈Dom(S),y∈S(x)}、Dom(S)={x∈X|S(x)≠∅}.

如果F是一个单值映射,那么SQVI(F,S)退化为:求x*∈S(x*)满足

〈F(x*),y-x*〉≥0, ∀y∈S(x*).

(2)

对于单值拟变分不等式(2),文献[13]首先定义了间隙函数f0(x):Rn→Rn∪{+∞}为

f0(x)=

-inf{〈F(x),y-x〉|y∈S(x)}.

(3)

在给定的条件下研究上述间隙函数f0(x)的连续性和可微性,同时也获得关于间隙函数f0(x)的最优化问题与拟变分不等式(2)之间的等价性.文献[14]定义单值拟变分不等式问题(2)的间隙函数fα(x):Rn→Rn为

fα(x)=max{-〈F(x),y-x〉-

αφ(x,y)|y∈S(x)}.

(4)

利用新定义的间隙函数,文献[14]对文献[13]的相关结果进行了推广.

另一方面,若对任意的x∈Rn,S(x)≡S,其中S⊂Rn为非空子集,则SQVI(F,S)退化为求x*∈S,u*∈F(x*)满足

〈u*,y-x*〉≥0, ∀y∈S.

(5)

若F是一个单值映射,对任意的x∈Rn,S(x)≡S,其中S⊂Rn为非空子集,则SQVI(F,S)退化为下面的变分不等式问题:求x*∈S满足

〈F(x*),y-x*〉≥0, ∀y∈S.

(6)

文献[15-16]定义(5)式的间隙函数fα(x):Rn→R为

fα(x)=

(7)

并获得间隙函数的相关性质.

在此之后,文献[11]利用(7)式定义问题(6)的新间隙函数

‖x-z‖}2,

证明关于φf(x,α,λ)的极小化问题与变分不等式问题(6)等价,并且研究φf(x,α,λ)的可微性,给出一些与误差界相关的结果.

在(6)和(7)式的基础上,文献[1]定义了集值变分不等式问题(5)的间隙函数f:Rn×(0,+∞)→Rn为

f(x;α)=

(8)

利用间隙函数(8),文献[1]推广了文献[11]中相应的结论.除此之外,文献[2]也将文献[11]的变分不等式问题推广为集值混合变分不等式,在给定的条件下,推广文献[11]中相应的结论.

受上述研究工作的启发,本文研究了集值拟变分不等式间隙函数的性质以及与误差界相关的结果,给出集值拟变分不等式新的间隙函数的定义,在给定的条件下,研究集值拟变分不等式间隙函数的相关性质以及与误差界相关的结果,推广了文献[1-2]的相应结论.

1 预备知识

1) 强单调的,如果存在μ>0使得∀x,y∈Rn,u∈F(x),v∈F(y)有

〈u-v,x-y〉≥μ‖x-y‖2;

2) 单调的,如果对∀x,y∈Rn,u∈F(x),v∈F(y)有

〈u-v,y-x〉≥0;

3) 伪单调的,如果对∀x,y∈Rn,u∈F(x),v∈F(y)有

〈u,y-x〉≥0⟹〈v,y-x〉≥0;

4) 关于x*强单调的,如果存在γ>0,对∀x∈S(x*),u∈F(x)有

〈u,x-x*〉≥γ‖x-x*‖2,

其中x*是SQVI(F,S)的解.

注 1.1 若F是关于x*强单调的,则SQVI(F,S)的解x*是唯一的[17].此外,如果x*是SQVI(F,S)的解,F是强单调的,则F是关于x*强单调的,其中强单调系数γ∈(0,μ).事实上,因为x*是SQVI(F,S)的解,则存在u*∈F(x*)使得下列不等式成立

〈u*,x-x*〉≥0, ∀x∈S(x*),

则对∀x∈S(x*),u∈F(x)有

〈u,x-x*〉≥μ‖x-x*‖2+〈u*,x-x*〉

≥μ‖x-x*‖2≥γ‖x-x*‖2.

1)M(x)≥0,∀x∈S(x);

2)M(x)=0,当且仅当x∈S(x)是问题(1)的解.

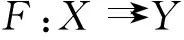
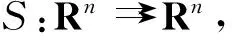
(y,x)⊂Graph(S),

则称映射S具有不动点对称性,显然,这种性质可表示为

∀x∈FP(S), ∀y∈S(x)⟹x∈S(y).

下面的引理1.1参看文献[18]的命题1.4.16.

).

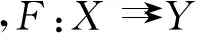
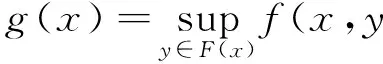
1) 若f和F是下半连续函数,则g(x)也是下半连续函数;

2) 若f是上半连续函数,F是上半连续函数并且是紧值的,则g(x)也是上半连续函数.

引理 1.2[19]令X是拓扑空间,φi:X→[-∞,+∞](i∈I)是下半连续函数,这里I是任意的指标集,则函数

下半连续.

2 间隙函数

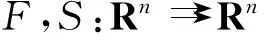
(9)

(10)

其中φ(x,y):Rn×Rn→R满足下列条件:

(C1)φ在Rn×Rn上连续可微;

(C2)φ在Rn×Rn上非负且φ(x,y)=0,当且仅当x=y;

(C3)φ(x,·)关于x是一致强凸的,即存在常数μ>0,对∀x∈Rn满足

φ(x,y1)-φ(x,y2)≥〈yφ(x,y2),y1-y2〉+

μ‖y1-y2‖2, ∀y1,y2∈Rn,

(C4)yφ(x,·)是Rn上具有模κ≥2μ的一致Lipschitz连续函数,也就是说,存在正数κ≥2μ使得对∀x∈Rn有

‖y(x,y1)-y(x,y2)‖≤κ‖y1-y2‖,

∀y1,y2∈Rn;

(C5) 对任意的x,y∈Rn,xφ(x,y)=-yφ(x,y).

注 2.1 易知,若φ(x,y)=‖x-y‖2,则φ(x,y)满足(C1)～(C5).在这种情况下,(9)式退化为

‖x-y‖2}.

特别地,当S(x)=K,∀x∈Rn,其中K⊂Rn为非空子集,则(9)式退化为参考文献[1]中所定义的函数

‖x-y‖2}.

参看文献[20]的引理2.1和引理4.2得引理2.1.

引理 2.1 令φ(x,y)满足(C1)～(C5),则有:

2) 对所有的x,y∈S(x),

μ‖x-y‖2≤φ(x,y)≤(κ-μ)‖x-y‖2,

其中μ和κ分别为(C3)和(C4)中的常数.

首先研究本文所定义的函数(9)和(10)式所具有的一些性质.

1) 对任意的α>0和x∈S(x),有fα(x)≥0;

2) 对任意的α>0和x∈Rn,存在u0∈F(x),使得fα(x)=gα(x,u0);

3) 如果F上半连续,则对任意α>0,fα是下半连续函数.

证明 1) 若x∈S(x),则y=x∈S(x),有0∈{〈u,x-y〉-αφ(x,y)},故由gα(x,u)的定义得gα(x,y)≥0,因此

2) 因为〈u,x-y〉-αφ(x,y)关于u是连续的,且S是下半连续映射,由引理1.1的1)知gα(x,u)关于u是下半连续的.又因F是紧值的,故存在u0∈F(x)使得fα(x)=gα(x,u0).

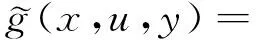
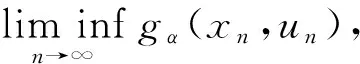
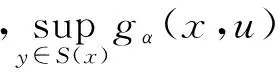
是下半连续函数.

证明 若fα(x*)=0,由fα(x)的定义,可得

因为S是下半连续的,由引理1.1的1)可知gα(x*,u)关于u是下半连续的,又因F(x*)是紧值的,则存在u*∈F(x*)使得

gα(x*,u*)=0.

因为〈u*,x*-y〉-αφ(x*,y)关于y是连续函数且S(x*)是紧值的,则由引理2.2,存在yα(x*)∈S(x*)满足

gα(x*,u*)=〈u*,x*-yα(x*)〉-

αφ(x*,yα(x*))=0，

因此,

〈u*,yα(x*)-x*〉=

-αφ(x*,yα(x*))≤0.

(11)

因为yα(x*)∈S(x*)是

gα(x*,u*)=

的解,则由最优性条件得

〈u*+αyφ(x*,yα(x*)),y-yα(x*)〉≥0,

∀y∈S(x*),

(12)

(12)式等价为

〈u*,yα(x*)-y〉≤

〈αyφ(x*,yα(x*)),y-yα(x*)〉,

∀y∈S(x*).

因为x*∈FP(S),故x*∈S(x*).取x*=y,可得

〈u*,yα(x*)-x*〉≤

〈αyφ(x*,yα(x*)),x*-yα(x*)〉.

(13)

另一方面,由条件(C3)得

φ(x*,x*)-φ(x*,yα(x*))≥

μ‖x*-yα(x*)‖2,

由于φ(x*,x*)=0,由(13)式可得

〈αyφ(x*,yα(x*)),x*-yα(x*)〉≤

-αμ‖x*-yα(x*)‖2-

αφ(x*,yα(x*)).

(14)

结合(13)和(14)式得

〈u*,yα(x*)-x*〉≤

-αμ‖x*-yα(x*)‖2-αφ(x*,yα(x*)).

根据(11)式可得

αμ‖x*-yα(x*)‖2≤0.

故x*=yα(x*),x*是SQVI(F,S)的解.事实上,因为x*=yα(x*)结合(12)式,可得

〈u*+αyφ(x*,x*),y-x*〉≥0,

∀y∈S(x*).

反之,如果x*是SQVI(F,S)的解,则x*∈S(x*)且存在u*∈F(x*)使得

〈u*,y-x*〉≥0, ∀y∈S(x*),

则

gα(x*,u*)=

由此可得

gα(x*,u*)≤0.

对任意的x*∈S(x*),由引理2.2的1)可得:fα(x*)≥0,fα(x*)=0.

注 2.2 1) 如果对任意的x∈Rn,S(x)=S是一个非空的闭集,φ(x,y)=‖x-y‖2,则引理2.3退化成文献[1]的引理3.3;

2) 如果F是一个单值映射,则引理2.3退化为文献[14]的引理2.2.此外,如果φ(x,y)=0,则引理2.3等价为文献[13]的定理2.

定义函数hβ:Rn→R∪{+∞}为

hβ(x)=

(15)

其中β≥0.显然,如果x∈S(x),则hβ(x)≥0.

证明 1) 如果x*是SQVI(F,S)的解,则x*∈S(x*)且存在u*∈F(x*),使得

〈u*,y-x*〉≥0, ∀y∈S(x*).

因为F是伪单调的,则有

〈v,y-x*〉≥0, ∀y∈S(x*),v∈F(y),

可得

因为对∀x*∈S(x*)和β≥0有hβ(x*)≥0,从而h0(x*)=0.

反之,如果h0(x*)=0,则有

〈v,x*-y〉≤0,

∀y∈S(x*),v∈F(y).

本文断言x*是SQVI(F,S)的解.若不然,因为x*∈S(x*),则存在y0∈S(x*),使得

〈u*,y0-x*〉<0, ∀u*∈F(x*).

令A={u*∈Rn:〈u*,y0-x〉<0},则A是F(x*)的邻域.因为x*,y0∈S(x*)且S(x*)是凸值的,则令xt=ty0+(1-t)x*∈S(x*),其中t∈(0,1].令t→0+,可得xt→x*,故存在x*的邻域U,使得对充分小的t>0,xt∈U.因为A是F(x*)的邻域,U是x*的邻域,且xt∈U,由F是上半连续函数,可知F(xt)⊂A.由此可知,对每一个ut∈F(xt)有

〈ut,y0-x*〉<0.

对ut∈F(xt),xt∈S(x*),有下面的不等式

〈ut,xt-x*〉=t〈ut,y0-x*〉<0,

这与任意的y∈S(x*),v∈F(y)有〈v,y-x*〉≥0相矛盾.

2) 若β>0且hβ(x*)=0,由hβ(x*)的定义可得

〈v,x*-y〉+βφ(x*,y)≤0,

∀y∈S(x*),v∈F(y).

因为φ(x*,y)≥0,则对所有y∈S(x*),v∈F(y),有〈v,x*-y〉≤0,后面的证明过程与引理2.4的1)的充分性证明相类似,由此可知x*是SQVI(F,S)的解.

反之,因为F关于SQVI(F,S)的解x*强单调的,故有

〈v,y-x*〉≥γ‖y-x*‖2,

∀y∈S(x*),v∈F(y).

(16)

(16)式等价于

〈v,x*-y〉≤-γ‖y-x*‖2,

∀y∈S(x*),v∈F(y).

由引理2.1的2)可得

〈v,x*-y〉+βφ(x*,y)≤

[β(κ-μ)-γ]‖x*-y‖2.

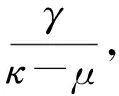
hβ(x*)=

又因为对x*∈S(x*)都有hβ(x*)≥0,从而hβ(x*)=0.

考虑下面2个函数

(17)

和

(18)

其中,λ>0,fα(·)、hβ(·)分别定义为(10)和(15)式,因此(17)和(18)式可写作

αφ(z,y)}}+λφ(x,z)}

(19)

和

βφ(z,y)}}+λφ(x,z)}.

(20)

下面将在不假设集值映射F可微的条件下,研究τf,α,λ(x)和τh,β,λ(x)的可微性.为了方便,对任意的α>0,β≥0,λ>0,分别定义ψf,α,λ(x,z):Rn×S(x)→(-∞,+∞]和ψh,β,λ(x,z):Rn×S(x)→(-∞,+∞]为

ψf,α,λ(x,z)=fα(z)+λφ(x,z),

ψh,β,λ(x,z)=hβ(z)+λφ(x,z).

因此,由(17)和(18)式所定义的τf,α,λ(x)、τh,β,λ(x)可改写为

定理 2.1 若对任意α,λ>0及x∈Rn,函数ψf,α,λ(x,·)在S(x)上取得唯一的最小值zf,α,λ(x)且zf,α,λ(x)连续,则τf,α,λ(x)在Rn上可微且

证明 由τf,α,λ(·)、ψf,α,λ(·,·)、zf,α,λ(·)的定义,对每一个d∈Rn和ξ>0有

τf,α,λ(x+ξd)-τf,α,λ(x)≤

ψf,α,λ(x+ξd,zf,α,λ(x))-ψf,α,λ(x,zf,α,λ(x))=

λφ(x+ξd,zf,α,λ(x))-λφ(x,zf,α,λ(x)).

因此,在不等式的最左端和最右端同时除以ξ且让ξ→0,可得

(21)

此外,对每一个d∈Rn和ξ>0,令xξ=x+ξd.由τf,α,λ(·)、ψf,α,λ(·,·)、zf,α,λ(·)的定义得

τf,α,λ(x+ξd)-τf,α,λ(x)=

τf,α,λ(xξ)-τf,α,λ(x)≥

ψf,α,λ(xξ,zf,α,λ(xξ))-

ψf,α,λ(x,zf,α,λ(xξ))=

λφ(x+ξd,zf,α,λ(x+ξd))-

λφ(x,zf,α,λ(x+ξd)).

因此,在不等式的最左端和最右端同时除以ξ且让ξ→0,结合zf,α,λ(·)的连续性有

(22)

注意到(16)和(17)式对每一个d∈Rn有

λ〈xφ(x,zf,α,λ(x)),d〉,

定理 2.2 若对任意β≥0,λ>0及x∈Rn,函数ψh,β,λ(x,·)在S(x)上取得最小值zh,β,λ(x),且zh,β,λ(x)连续,则τh,β,λ(x)在Rn是可微的,且

证明 证明过程与定理2.1相类似.

3 误差界

利用fα(·)、hβ(·)、τf,α,λ(·)、τh,β,λ(·)研究集值拟变分不等式问题(1)的误差界.

fα(x)≥[γ-α(κ-μ)]‖x-x*‖2,

∀x∈S(x*).

证明 因为F(x)是紧值的,且S是下半连续的,由引理2.2的2),对任何的x∈Rn,存在vx∈F(x),使得

fα(x)=gα(x,vx).

因为F是关于x*强单调的,则有

〈vx,x-x*〉≥γ‖x-x*‖2.

另一方面,因为S具有不动点对称性,对任意的x∈S(x*),显然有x*∈S(x).由引理2.1的2)可得

fα(x)=gα(x,vx)=

〈vx,x-x*〉-αφ(x,x*)≥

γ‖x-x*‖2-α(κ-μ)φ(x,x*)≥

[γ-α(κ-μ)]‖x-x*‖2.

hβ(x)≥μβ‖x-x*‖2, ∀x∈S(x*).

证明 因为x*是SQVI(F,S)的解,则x*∈S(x*)且存在u*∈F(x*)使得

〈u*,x-x*〉≥0, ∀x∈S(x*).

因为S具有不动点对称性,故对任意x∈S(x*)都有x*∈S(x).由引理2.1的2)可得

〈u*,x-x*〉+βφ(x,x*)≥

βφ(x,x*)≥μβ‖x-x*‖2.

‖x-x*‖2≤

τf,α,λ(x)≤λ(κ-μ)‖x-x*‖2,

∀x∈S(x*).

证明 因为x*是SQVI(F,S)的解,则x*∈S(x*).由引理2.3有

fα(x*)=0.

对任意的x∈S(x*),因为S是不动点对称的,则有x*∈S(x),结合引理2.1的2)可得

fα(x*)+λφ(x,x*)≤λφ(x,x*)≤

λ(κ-μ)‖x-x*‖2.

根据引理3.1可得

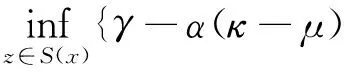
由不等式

∀a,b∈Rn,

则

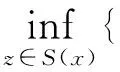
‖z-x*‖2+‖x-z‖2}≥

从而

τf,α,λ(x)≥

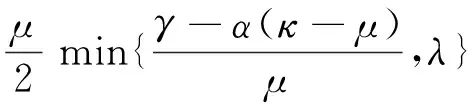
‖x-x*‖2≤

τh,β,λ(x)≤λ(κ-μ)‖x-x*‖2,

∀x∈S(x*).

证明 对任意的x∈S(x*),因为S是不动点对称的,则x*∈S(x).由x*是SQVI(F,S)的解,由引理2.4,可知hβ(x*)=0,右边的不等式证明类似于定理3.1的证明.此外,结合引理3.2,左边的不等式证明跟定理3.1最后一部分证明类似.

1) 若F、S是紧值的且S下半连续的,对任意的λ>0和x∈S(x*),则x*是SQVI(F,S)的解当且仅当τf,α,λ(x*)=0;

2) 若F是上半连续的且S是凸值的,对任意的λ>0和x∈S(x*),则x*是SQVI(F,S)的解当且仅当τh,β,λ(x*)=0.

证明 1) 如果x*是SQVI(F,S)的解,则x*∈S(x*).对任意x∈S(x*),让x=x*,由定理3.1可得τf,α,λ(x*)=0.

反之,若τf,α,λ(x*)=0,由τf,α,λ(·)的定义可知,对任意的z∈S(x*)有

fα(z)+λφ(x*,z)≥0.

因为fα(z)+λφ(x,z)关于z是下半连续的且S是紧值的,则存在极小化序列{zn}∈S(x*)使得对任意的正整数n有

fα(zn)+λφ(x*,zn)≤

即存在序列{zn}∈S(x*),使得fα(zn)→0和φ(x*,zn)→0,则zn→x*.因为集合S(x*)是闭的,且zn∈S(x*),从而x*∈S(x*).由引理2.2可知fα(·)是下半连续和非负的,则有

0≤fα(x*)≤

因此,fα(x*)=0,从而,由引理2.3可知x*是SQVI(F,S)的解.

2) 如果x*是SQVI(F,S)的解,则x*∈S(x*).对任意的x∈S(x*),让x=x*.又因为F是上半连续的且S是凸值的,由定理3.2可得τh,β,λ(x*)=0.反之,如果τh,β,λ(x*)=0,证明过程与定理3.3的1)的充分性证明相似.

[1] FAN H J, WANG G X. Gap functions and global error bounds for set-valued variational inequalities[J]. Comput Appl Math,2010,233(11):2956-2965.

[2] TANG G J, HUANG N J. Gap functions and global error bounds for set-valued mixed variational inequalities[J]. Taiwanese J Math,2013,17(4):1267-1286.

[3] HUAN L, JIANG B. Merit functions for general mixed qusi-variational inequalities[J]. J Appl Math Comput,2010,33(1):411-421.

[4] CHARITHA C, DUTTA J. Regularized gap functions and error bounds for vector variational inequalities[J]. Pac J Optim,2010,6(3):497-510.

[5] AUSSEL D, CORREA R, MARECHAL M. Gap functions for quasi-vatiational inequalities and generlized nash equilibrium problems[J]. J Optim Theory Appl,2011,151(151):474-488.

[6] AUSSEL D, GUPTA R, MARECHAL A. Gap functions and error bounds for quasi-vatiational inequality problems[J]. J Math Anal Appl,2013,407(2):270-280.

[7] SOLODOV M V, TSENG P. Some methods based on theD-gap function for solving monotone variational inequalities[J]. Comput Optim Appl,2000,17(2/3):255-277.

[8] HUANG L R, NG K F. Equivalent optimization formulations and error bounds for variational inequality problems[J]. J Optim Theory Appl,2005,125(2):299-314.

[9] HUANG N J, LI J, WU S Y. Gap functions for a system of generalized vector quasi-equilibrium problems with set-valued mappings[J]. J Global Optim,2008,41(3):401-415.

[10] FACCHINEI F, PANG J S. Finite-dimensional Vaeiational Inequalities and Complementary Problems[M]. New York:Spring-Verlag,2003.

[11] YAMASHIMA N, FUKUSHIMA M. Equivalent uncontrained minimization and global error bounds for variational inequality problems[J]. SIAM J Control Optim,1997,35(35):273-284.

[12] 夏福全,黎小波. Banach空间中分离变分不等式的 Levitin-Polyak-α适定性[J]. 四川师范大学学报(自然科学版),2012,35(3):430-434.

[13] FUKUSHIMA M. A class of gap functions for quasi-variational inequality problems[J]. J Ind Mang Optim,2007,3(2):165-171.

[14] TAJI K. On Gap functions for quasi-variational inequalities[J]. Abst Appl Anal,2008,2008:1563-1569..

[15] AUSLENDER A. Optimisation:Mecutethods Neumeriques[M]. Paris:Masson,1976.

[16] HEAM D W. The gap function of a convex program[J]. Oper Res Lett,1982,1(2):67-71.

[17] SOLODOV M.V. Merit functions and error bounds for generalized variational inequalities[J]. J Optim Theory Appl,2003,287(2):405-414.

[18] AUBIN J P, FRANKOWSKA H. Set-valued Analysis[M]. Boston:Birkhauser,1990.

[19] 福岛雅夫. 非线性最优化基础[M]. 北京:科学出版社,2011.

[20] YAMASHITA N, TAJI K, FUKUSHIMA M. Unconstrained optimization reformulations of variational inequality problems[J]. J Optim Theory Appl,1997,92(3):439-456.

2010 MSC：47H05; 47H04; 49J40; 49J30

(编辑 郑月蓉)

Gap Functions and Error Bounds for Set-valued Quasi-variational Inequalities

YANG Bo, XIA Fuquan

(College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan)

In this paper, we consider the gap functions for set-valued quasi-variational inequalities. Using these gap functions, we show the equivalence between optimization problem and the set-valued quasi-variational inequalities. With the obtained equivalence results, we study error bounds for the solutions of set-valued quasi-variational inequalities(Fan H J, Wang G X. Comput Appl Math,2010,233:2956-2965, and Tang G J, Huang N J. Taiwanese J Math,2013,17:1267-1286.).

gap function; set-valued map; quasivariational inequality; error bound

2016-03-27

教育部科学技术重点项目(212147)

O176; O178

A

1001-8395(2016)06-0801-08

10.3969/j.issn.1001-8395.2016.06.004

*通信作者简介：夏福全(1973—),男,教授,主要从事分拆理论与优化算法设计的研究,E-mail::fuquanxia@163.com