一类Wick型随机混合KdV方程的精确解

舒 级, 曾群香

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

一类Wick型随机混合KdV方程的精确解

舒 级, 曾群香

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

首先运用Hermite变换将Wick型随机KdV方程转换为确定性KdV方程,然后利用截断展开法得到方程的白噪声泛函解.

白噪声泛函解; Wick型随机混合KdV方程; 截断展开法; Hermite变换

1 预备知识

J. S. Russell[1]在“论波动”为题所做的报告中谈到:“沿着狭窄的河道迅速前进着,突然停下来了,河道内被船体带动的水团并不停止,它们积聚在船头周围剧烈的扰动着,然后形成了一个滚圆而又平滑、轮廊分明的巨大孤立波峰”,他把此种水波称为孤立波.荷兰著名数学家D. J. Korteweg等[2]建立了浅水波运动方程,其一般形式可写为

ut±6uux+uxxx=0,

称为Korteweg-deVries(KdV)方程,随后利用行波变换求出了与J.S.Russell所发现的孤立波现象一致的、具有形状不变的脉冲状孤立波解.此种解与C.S.Gardner等[3]利用反散射方法求出KdV的孤子解一致.美国应用数学家N.J.Zabusky等[4]数值模拟了孤立波相撞过程,得到了孤立波在碰撞后仍然保持其波形和速度不变或者只有微弱变化的性质.这种性质与物理中粒子的性质类似,因此把此种孤立波称为孤立子.此后科学家对孤立子的研究兴趣和热情便一发不可收拾.迄今为止,在许多科学领域都发现了孤立子运动形态,如神经细胞轴突上传导的冲动、流体中的漩涡、晶体的错位、木星上的红斑、等离子体中的声波和电磁波、激光在介质中的自聚焦等.在数学上,孤立子理论[5]的进展体现在发现了一大批具有孤立子解的非线性偏微分方程,并且逐渐形成了较为系统的数学物理的偏微分方程与孤子理论.

随机偏微分方程类似于一般的随机微分方程,其本质上是带有随机项和随机系数的偏微分方程.随机微分方程在量子场论、统计力学、金融数学中有着广泛的应用.更有意思的是,由于加入了随机项,因此求出的精确解并不是通常意义下的精确解[6-15],而是带有白噪声的泛函解,也就是带随机项的解.

M.Waditi[16]通过反散射方法求出了非线性随机KdV方程的精确解,进而提出带随机扰动项的理论基础.H.Holden等[17]把白噪声分析法引进方程,提出了Wick型随机偏微分方程.由于在实际问题中,带随机扰动的方程更有意义,因此越来越多的学者开始研究随机偏微分方程.B.Chen等[18]研究了随机mKP方程,H.Kim等[19]研究了变系数的广义随机Boussinesq方程组及随机KP方程.

本文将运用Hermite变换和截断展开法研究如下Wick-型随机混合KdV方程

Ut(t,x)+A0(t)◇Ux(t,x)+

A1(t)◇U(t,x)◇Ux(t,x)+

A2(t)◇U◇2(t,x)◇Ux(t,x)+

B(t)◇Uxxx(t,x)=0,

(1)

其中,◇是Kondratiev分布空间(S)-1上的Wick乘积,A0(t)、A1(t)、A2(t)和B(t)是定义在(S)-1上的白噪声泛函,且A0(t),A1(t),A2(t)和B(t)≠0.

2 求解Wick型随机偏微分方程的基本思路

对于随机偏微分方程

P(t,x,∂t,x,U,ω)=0,

(2)

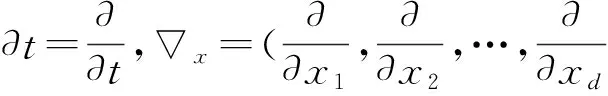
设方程(2)的Wick积具有如下形式

P◇(t,x,∂t,x,U,ω)=0.

(3)

然后,通过Hermite变换将方程(3)的Wick积变为普通乘积

(4)

z=(z1,z2,…)∈Kq(R),

Kq(R)={z=(z1,z2,…)∈CN,

成立,则在一定条件之下,通过Hermite变换的逆变换,就能得出方程(3)的一个解U,这一过程可以通过下述定理来实现.

定理 2.1 假定u(t,x,z)为方程(4)的一个解,其中(t,x)为某个G⊂R×Rd的有界开集元素,对于某些q和R有z∈Kq(R)成立.此外,假定u(t,x,z)以及方程中所有u(t,x,z)的偏导对于(t,x,z)∈G×Kq(R)是有界的,对z∈Kq(R)关于(t,x)∈G是连续的,对(t,x)∈G关于z∈Kq(R)是解析的.由文献[20]知,则存在U(t,x)∈(S)-1对所有的(t,x,z)∈G×Kq(R)使得

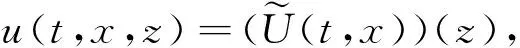
从而可以在(S)-1中用U(t,x)解方程(3)(在(S)-1中是强指向的).

3 截断展开法

截断展开法主要用来求解类孤子解,其基本步骤如下.

1) 为了得到非线性偏微分方程

P(t,x,u,ut,ux,uxt,uxx,utt,…)=0

(5)

的类孤子解,假定方程(5)的解的形式可表示成如下的截断展开形式

(6)

其中,An(t)(0≤n≤N)、f(t)和g(t)是一些待定函数;

2) 根据领头项分析,确定N的取值;

3) 求出ut、ux、uxxx,并将它们代入原方程,得到关于F的线性方程组.由于Fi(i=0,1,2,3,4)线性无关,令其前面的系数为零,得到非线性微分方程组,解方程组可以求出A0、A1、f(t)和g(t).

证明 因为有

(7)

所以上述性质成立.

4 截断展开法在求解Wick型随机混合KdV方程中的应用

对于Wick型随机混合KdV方程(1),通过Hermite变换可将方程中的Wick乘积化为普通乘积

Ut(t,x,z)+A0(t,z)Ux(t,x,z)+

A1(t,z)U(t,x,z)Ux(t,x,z)+

A2(t,z)U2(t,x,z)Ux(t,x,z)+

B(t,z)Uxxx(t,x,z)=0.

(8)

为了简便,记

Ut(t,x,z)=ut(t,x,z),A0(t,z)=α0(t,z),

Ux(t,x,z)=ux(t,x,z),A1(t,z)=α1(t,z),

U(t,x,z)=u(t,x,z),A2(t,z)=α2(t,z),

B(t,z)=β(t,z),Uxxx(t,x,z)=uxxx(t,x,z),

则方程(8)记为

ut(t,x,z)+α0(t,z)ux(t,x,z)+

α1(t,z)u(t,x,z)ux(t,x,z)+

α2(t,z)u2(t,x,z)ux(t,x,z)+

β(t,z)uxxx(t,x,z)=0.

(9)

对方程(9)进行领头项分析可知N=1,因此方程具有如下行波解

u(x,t,z)=A0(t,z)+A1(t,z)F,

(10)

其中

A0(t,z)和A1(t,z)待定.

根据(10)式可得:

ut(x,t,z)=A0t(x,t,z)+A1t(t,x,z)F+

A1(t,x,z)(F2-F)ξt,

(11)

ux(x,t,z)=A1(t,z)(F2-F)ξx,

(12)

uxxx(x,t,z)=

(13)

将(11)～(13)式代入方程(9),比较F前各个幂项前的系数得到:

F0:A0t=0,

(14)

F1:A1t-A1tξt-α0A1ξx-α1A0A1ξx-

(15)

(16)

(17)

(18)

从(14)、(15)和(18)式可求出:

A0(t,z)=C1(z),

(19)

A1(t,z)=C2(z),

(20)

其中,C1(z)和C2(z)是关于z的白噪声泛函.由(16)式得到

(21)

ft,z=0,

(22)

gt,z=-α0ξx-α1A0ξx-

(23)

解(22)和(23)式得到:

f(t,z)=C3(z),

(24)

g(t,z)=C4(z)t,

(25)

其中,C3(z)和C4(z)为白噪声泛函.将(24)和(25)式代入方程(22)和(23),经计算后发现自动成立,说明该设定的截断展开是自恰的,并考虑到关系

(26)

将(19)、(20)、(24)和(25)式代入(10)式,得到混合KdV方程的类孤子解

(27)

其中C5(z)和C6(z)为白噪声泛函,

ξ=C3(z)x+C4(z)t.

对精确解进行模拟,得到随机混合KdV方程的双曲正切函数,通过代入法验证了(27)式是方程(9)的解.

为了得到方程(1)的随机精确解,需要给出如下条件.

假设(x,t)为属于一个有界开集G⊂R+×R的元素,对于某些q>0,r>0的所有z∈Kq(r),使得A0(t,x)、A1(t,x)、A2(t,x)和B(t,x)满足u(t,x,z)在方程(1)中所有的偏导对(t,x,z)∈G×Kq(r)一致有界,并且对所有的z∈Kq(r)关于(t,x)∈G是连续的,对所有(t,x)∈G关于z∈Kq(r)是解析的.

由此条件以及定理2.1可知:存在U(t,x)∈(S)-1,使得对于所有的(t,x,z)∈G×Kq(r)有

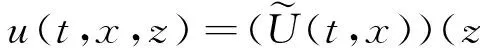
令U(t,x)是u(t,x,z)的Hermite逆变换,则由方程(9)的解(27)式可得到方程(1)的白噪声泛函解

(28)

其中

ξ=C3(z)◇x+C4(z)◇t.

[1] RUSSELL J S. Report on Waves[C]//London:Report of the 14th Meeting of the British Association for the Advancement of Science,1844:90-311.

[2] KORTEWEG D J, DE VRIES G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves[J]. Philosophical Magazine,1895,39(5):422-443.

[3] GARDNER C S, GREEN J M, KRUSKAL M D, et al. Method for solving the Korteweg-de Vries equation[J]. Phys Rev Lett,1967,19(19):1095-1097.

[4] ZABUSKY N J, KRUSKAL M D. Interaction of solitons in a collisionless plasma and the recurrence of initial states[J]. Phys Rev Lett,1965,15(6):240-243.

[5] 郭玉翠. 非线性偏微分方程[M]. 北京:清华大学出版社,2008.

[6] DAI Z D, LI S L, DAI Q Y, et al. Singular periodic solliton solutions for the KP equation[J]. Appl Math Comput,2010,216(5):1599-1604.

[7] XU G Q. The soliton solutions, dromions of the Kadomtsev-Petviashvili and Jimbo-Miwa equations in (3+1)-dimensions[J]. Chaos, Solitons & Fractals,2006,30(1):71-76.

[8] BOUNTIS T C. Singularities and Dynamical Systems[M]. New York:North-Holland,1985.

[9] MA W X. Complexiton solutions to the Korteweg-de Vries equation[J]. Phys Lett,2002,A301:35-44.

[10] MA H C, DENG A P, WANG Y. Exact solution of a KdV equation with variable coefficients[J]. Appl Math Comput,2011,61(8):2278-2280.

[11] TRIKI H, WAZWAZ A M. Traveling wave solutions for fifth-order KdV type equations with time-dependent coefficients[J]. Commun Nonlinear Sci Numer Simulat,2014,19(3):404-408.

[12] GANJI D D, ABDOLLAHZADEH M. Exact travelling solutions for the Lax’s seventh-order KdV equation by sech method and rational exp-function method[J]. Appl Math Comput,2008,206(1):438-444.

[13] GUO Z H, KWAK C, KWON S. Rough solutions of the fifth-order KdV equations[J]. J Functional Analysis,2013,265(11):2791-2829.

[14] TRIKI H, TAHA T R, WAZWAZ A M. Solitary wave solutions for a generalized KdV-mKdV equation with variable coefficients[J]. Math Comput Simul,2010,80(9):1867-1873.

[15] FAN E G. Soliton solutions for a generalized Hirota-Satsuma coupled KdV equation and a coupled MKdV equation[J]. Phys Lett,2001,A282(1/2):18-22.

[16] WADITI M. Stochastic Korteweg-de Vries equation[J]. J Phys Soc Jpn,1983,52(8):2642-2648.

[17] HOLDEN H, OKSENDAL U B, ZHANG T. Stochastic Partial Differential Equations:a Modeling, White Noise Functional Approach[M]. Boston:Birhkauser,1996.

[18] CHEN B, XIE Y C. Exact solutions of the Wick-type stochastic mKP equations[J]. Chaos, Solitions & Fractals,2007,31(1):173-178.

[19] KIM H, SAKTHIVEL R. Exact solutions of Wick-type stochastic equations with variable coefficients[J]. Reports Math Phys,2011,67(10):415-429.

[20] CHEN B, XIE Y C. Periodic-like solutions of variable coefficient and Wick-type stochastic NLS equations[J]. J Comput Appl Math,2007,203(1):249-263.

[21] 范恩贵. 可积系统与计算机代数[M]. 北京:科学出版社,2004.

[22] 曾群香,黄欣,舒级,等. Wick-型混合随机KdV方程的精确解[J]. 四川师范大学学报(自然科学版),2015,38(1):27-33.

[23] 廖欧,舒级,曾群香. 一类混合KdV方程的精确孤立波解[J]. 四川师范大学学报(自然科学版),2015,38(4):493-496.

2010 MSC：35Q55

(编辑 李德华)

收稿日期:2016-08-15

基金项目：四川省教育厅重点科研项目(14ZB0065)基金和四川省科技厅基金项目(K33)

*通信作者简介：莫智文(1962—),男,教授,主要从事人工智能、模糊语言、粗糙集和量子信息处理的研究,E-mail:mozhiwen@263.net

Exact Solutions for a Class of Wick-type Mixed Stochastic KdV Equations

SHU Ji, ZENG Qunxiang

(College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan)

First we converse the Wick-type stochastic KdV equation to a determining KdV equation with Hermite transformation, then obtain white noise functional solutions of the KdV equation by the truncation expansion method.

white noise functional solutions; Wick-type mixing stochastic KdV equation; truncation expansion method; Hermite transformation

2015-06-04

国家自然科学基金(11371267)、四川省教育厅重点科研基金(14ZA0031)和四川省科技厅应用基础计划(2016JY0204)

舒 级(1976—),男,副教授,主要从事偏微分方程的研究,E-mail:shuji2008@hotmail.com

O175.29

A

1001-8395(2016)06-0821-04

10.3969/j.issn.1001-8395.2016.06.007