基于河谷横剖面形态特征的滑坡体堵江易发性评价研究

王珊珊,童立强

(中国国土资源航空物探遥感中心,北京100083)

基于河谷横剖面形态特征的滑坡体堵江易发性评价研究

王珊珊,童立强

(中国国土资源航空物探遥感中心,北京100083)

滑坡体堵江易发性评价是滑坡堵江风险研究中的短板,不利于其防灾减灾工作的开展。该文以物质来源、水力条件和河谷地形为主要影响因素进行滑坡体堵江概率预测分析和应用,提供了基于GIS技术的河谷横剖面形态参数自动提取方法,以定量表征河谷地形特征;以中国喜马拉雅山地区为例,分别提取堵江滑坡和非堵江滑坡事件为样本,基于逻辑回归建立了研究区滑坡体堵江概率预测模型,经验证精度较理想。取得的主要结论有:1)河谷横剖面形态参数自动提取方法,具有面向对象、表征全面、提高计算效率和精度等优点。2)在中国喜马拉雅山地区,堵江滑坡事件与非堵江滑坡事件发生处河谷横剖面的坡高、不同深度宽深比、凹度和河宽指数具有显著差异,其中河宽指数差异最大,3/4坡高宽深比次之。3)基于逻辑回归开展滑坡体堵江易发性评价是可行的,该方法在中国喜马拉雅山地区的应用精度达80%以上,各变量按照与滑坡体堵江形成的相关性从大到小依次是坡高宽深比、滑坡面积、工程地质岩组、河宽指数和凹度。

滑坡堵江;河谷横剖面;自动提取;逻辑回归

0 引言

滑坡堵江是滑坡堆积体向下运动、推移,堵塞山间河流的现象,一定规模的滑坡堵江事件常常在坝体形成、回水淹没或坝体失稳、洪水溃决的过程中造成巨大破坏[1,2]。针对滑坡堵江的链式过程,已有学者围绕滑坡发生危险性[3]、滑坡坝体稳定性[4-6]、溃决洪水演进模拟[7]和承灾体灾损分析[8]等问题开展了较为广泛的研究,但针对滑坡发生后堆积体堵江可能性的评价却涉及甚少,尚未取得较成熟的研究成果。这使滑坡堵江风险研究缺少了承上启下的重要环节,不利于防灾减灾工作的开展。

滑坡堆积体能否堵江的主要控制因素可以概括为物质来源、水力条件和河谷地形[9,10]。物质来源和水力条件可通过实地调查获取,在区域分析中常用工程地质岩组、上游流域面积等参数表征。就地形而言,目前常用的地形参数包括坡度、坡向、粗糙度、起伏度等,尚无法有效表征河谷的具体形态。针对这一问题,本文提出了表征河谷地形的河谷横剖面形态参数及其自动提取方法,在此基础上基于逻辑回归建立了滑坡体堵江概率预测模型,并在我国喜马拉雅地区的应用中取得了理想的评价效果,从而证明了基于河谷横剖面特征开展滑坡体堵江易发性评价是可行的。

1 河谷横剖面形态参数与自动提取

河道上任意一点的河谷横剖面是由垂直于该点流向的谷底河道及两岸斜坡组成的几何体,其形态沿河流方向不断变化。河谷横剖面几何形态的定量计算和分析,将有助于判断河谷类型和发育情况。

1.1 河谷横剖面形态参数

目前河谷横剖面特征的定量研究并不多见。Zhou等曾基于DEM数据提取了日本山区河谷横剖面上高程的最值、均值、标准差、偏差等统计参数[11,12]。闵石头等从几何角度,利用宽深比、凹度、不对称系数等参数分析了滇西纵向岭谷区河谷横剖面的形态特征[13]。相比之下后者更能突出河谷横剖面的微观地形特征,本文在其基础上进行改进,提出了可用于滑坡体堵江易发性评价的河谷横剖面形态参数,图1是河谷横剖面的几何示意图。

(1)坡高h。即河谷左、右两岸斜坡山脊与河谷最低点高差的较小值,h=min(h1,h2)。

(2)宽深比R。取谷深h′,且h′＜h,在h′深度上向两岸斜坡作水平线,得到谷宽l′,宽深比R=l′/h′。h′可以取多个值,以全面反映河谷在不同深度上的宽窄程度。

图1 河谷横剖面几何示意Fig.1 The geometric graphic of valley transverse profile

(3)剖面面积A。以坡高相对较低的山脊为顶点,以坡高h所对应的谷宽l为长,以坡高h为宽做矩形ra。河谷横剖面将ra分为上下两部分,上部封闭空间的面积为剖面面积A。一般A越大,堵江所需滑坡堆积体的体积越大。

(4)凹度C。矩形ra中,上部与下部封闭空间的面积之比为凹度,即C=A/(Ara-A),其中Ara为矩形ra的面积。凹度可表征河谷的形态类型:C＞1时,定义河谷为U形谷;当C≤1时,定义河谷为V形谷。一般V形谷有利于形成滑坡堵江。

(5)不对称系数S。即河谷最低点到矩形ra左、右两条宽边的水平距离之比,S=w1/w2。S=1时河谷两岸对称,反之为左倾型或右倾型河谷。

(6)河宽指数W。河道宽度一般通过遥感影像解译或现场量测获取,费时费力且误差较大。本文提出河宽指数的概念以表征同一区域内不同河谷横剖面上河宽的相对大小。计算方法是从河谷横剖面的最低点分别向两岸斜坡做角度为θ的射线并交于两点,该两点间的水平距即为河宽指数。θ的取值和精度主要由区域地形复杂性和DEM数据质量决定。

1.2 基于DEM的参数自动提取

目前河谷横剖面形态参数主要借助地学分析软件和地图手动量算获得,不仅操作复杂、效率较低,且精度易受干扰,导致相关应用研究难以开展。本文基于GIS软件和二次程序编写实现了河谷横剖面形态参数的自动提取。具体流程如图2所示,输入数据是覆盖河谷流域的DEM和分布在河道附近的定位点,参数提取过程涉及河谷横剖面水平投影线生成、采样点提取和形态参数计算3个步骤。

(1)河谷横剖面水平投影线生成。定位点处河谷横剖面水平投影线的方向与该点处的河流流向垂直,因此首先要计算定位点的河流流向。GIS软件可以基于DEM自动提取河流流向,但所得数据只能表示离散的8个方向,与实际情况常常偏差较大。针对这一问题,本文基于最小二乘法实现了连续型河流流向的自动提取。首先基于ArcGIS水文分析提取河流矢量线并进行编号,然后如图3所示,按照采样间隔a提取河流采样点集合P。其中a取值为略大于2倍DEM空间分辨率的正整数。检索出距离定位点最近的河流采样点Pi,将其河流流向作为定位点的河流流向。Pi处河流流向的计算方式如下:以Pi为起点分别向上、下游各遍历3个采样点,根据上述7个采样点的二维坐标基于最小二乘法进行直线拟合,所得直线的斜率k即为Pi处的河流流向,k的计算公式为:

图2 河谷横剖面形态参数自动提取流程Fig.2 The automatic extraction flow of valley transverse profile morphological parameters

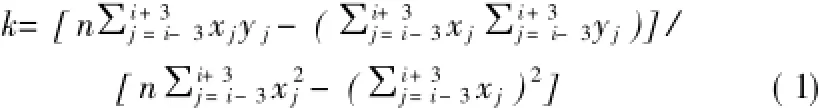
图3 河谷横剖面水平投影线示意Fig.3 The graphic of horizontal projection line of valley transverse profile

借助ArcGIS地形分析和图形编辑工具获取河谷内的线状山脊矢量数据。为每条山脊线添加关联河流编号river_id和相对位置l_r两个属性,表征该山脊线位于某条河流的左岸还是右岸。在此基础上,过定位点以K=-1/k为斜率做射线分别交左、右两岸山脊于A、B点,线段A B即为河谷横剖面的水平投影线。

(2)河谷横剖面采样点提取。在线段A B上,从左端点开始按照采样间隔b提取采样点直至右端点。将距离河流线最近的点视为河谷最低点,编号为id=0;以此为中心分别按顺序对左、右两侧采样点进行编号,定义右侧采样点id=1,2,3,…,左侧采样点id=-1,-2,-3,…。计算各采样点的高程H和距离0点的水平距离len。

(3)形态参数计算。按照河谷横剖面形态参数的定义,利用提取的河谷横剖面采样点及其属性值,计算定位点处河谷横剖面的坡高h、宽深比R、剖面面积A、凹度C、不对称系数S和河宽指数W等形态参数。

1.3 主要优势

河谷横剖面形态参数自动提取程序基于ArcEngine二次开发平台和Visual Studio 2010开发环境,采用C#高级语言编写完成。相比于坡度、坡向、粗糙度、起伏度等常用地形参数,本文所采用的河谷横剖面形态参数及其获取方式主要具有以下优势:

(1)面向对象:以沿河流分布的任意一点为对象,自动提取其河谷横剖面形态特征参数,几何意义表征明确,能够从微观上反映河谷地貌及分段差异,有利于分析河谷的整体地形。

(2)表征全面:河谷横剖面的坡高、宽深比、横剖面面积、凹度、不对称系数、河宽指数等形态特征参数,可以共同反映河流的整体形态、地势变化和切割程度等,表达全面完整。

(3)干扰因素小,精度更高:形态参数自动提取的输入数据和设置较少,包括DEM、定位点位置、采样间隔和计算间隔,误差主要源于DEM数据质量和空间采样,人为干扰程度低,提高了参数的计算精度。

(4)运算效率提高:以沿河分布的定位点为计算对象,待计算点数目减少,有利于提高计算效率,节约存储空间;另外可同时完成所有特征参数的计算,操作简单,可维护性强。

2 中国喜马拉雅山地区滑坡堵江河谷横剖面特征分析

2.1 研究区概况

中国喜马拉雅山地区位于青藏高原南部,西起阿里,东至林芝,北到雅鲁藏布江,南与印度、尼泊尔、不丹接壤;东西长约1 700 km,南北宽60～250 km,总面积约1.68×105km2。喜马拉雅山是近东西向的弧形山系,由许多平行的山脉组成,平均海拔6 000 m以上。山脉南坡陡峻,北坡平缓,地形起伏变化大,具有分带性。研究区绝对高度大于4 000 m的高位地貌占总面积的79%;相对高程大于500 m的山地约占86%。在欧亚板块与印度洋板块的碰撞下,区内构造运动强烈,地形切割破碎,滑坡、崩塌、泥石流等地质灾害频发,在破坏生态环境平衡的同时,严重制约了当地社会经济的正常发展[14]。众多失稳斜坡在高山峡谷中常常形成堵江事件,为滑坡体堵江的易发性研究提供了宝贵素材。

2.2 数据获取

本文选用覆盖中国喜马拉雅山地区30 m分辨率的AST ER GDEM v2为高程数据源,通过遥感影像解译和现场调查获取了研究区堵江滑坡定位点90个和非堵江滑坡定位点91个。本文中的“滑坡”为狭义滑坡,不包含崩塌、泥石流等斜坡运动以及冰川活动形成的物质运动形式。考虑到滑坡运动及气候、人类活动等因素对河谷横剖面原始形态的改造,定位点多选在邻近滑坡的原始河谷地形变化较小的上游河道上,对周围原始地形变化过大的滑坡事件则不予采用。

基于以上数据,设置河流纵剖面采样间隔和横剖面采样间隔为40 m,θ为11.3°,自动提取了上述两类定位点的河谷横剖面形态参数,包括坡高、坡高宽深比、3/4坡高宽深比、1/2坡高宽深比、1/4坡高宽深比、横剖面面积、凹度、不对称系数和河宽指数。

2.3 河谷横剖面特征分析

研究区堵江滑坡和非堵江滑坡定位点处河谷横剖面形态参数的差异性统计结果见表1。坡高、不同深度宽深比、凹度和河宽指数的样本差异性统计量Z均大于z0.025=1.96,剖面面积和不对称系数的差异性统计量Z小于该值,可以认为在显著性水平0.05条件下,中国喜马拉雅山地区堵江滑坡与非堵江滑坡发生处河谷横剖面的坡高、不同深度宽深比、凹度和河宽系数具有显著差异,其中河宽指数差异最大,3/4坡高宽深比次之。

堵江滑坡河谷横剖面的宽深比普遍偏小,集中在2.5～4.5之间;非堵江滑坡河谷横剖面的宽深比分布相对离散,取值多大于4。堵江滑坡河谷凹度的平均值为0.958,最大值为1.476;非堵江滑坡河谷凹度的平均值为1.184,最大值为2.655,大于1的样本占总数的65.9%,这反映出V形谷比U形谷更利于形成滑坡堵江。河宽指数的最大值、平均值在两类定位点间差异性更明显。研究区堵江滑坡与非堵江滑坡河谷横剖面的剖面面积和不对称系数不具有明显差异,一定程度上说明这两个参数对滑坡体堵江形成不具有决定性作用。可见,坡高、宽深比、凹度和河宽指数是滑坡体堵江形成的主要地形因素。

此外,本文提取并统计了两类定位点处原始斜坡的平均坡度,得出差异性统计量Z为2.070,略大于z0.025,但明显小于河谷横剖面坡高、不同深度宽深比、凹度和河宽指数的差异性统计量Z。可见,河谷横剖面参数更适于参与滑坡体堵江易发性评价。

表1 河谷横剖面形态参数差异性统计Table 1 The difference statistics of valley transverse profile morphological parameters

3 基于逻辑回归的滑坡体堵江概率预测模型

本文以研究区的堵江滑坡和非堵江滑坡事件为样本,获取两类样本在物源、水力和地形等方面的定性、定量特征参数作为变量,基于逻辑回归模型构建函数来表征滑坡发生后堆积体堵江的概率,以实现滑坡体堵江能力的定量评价。

3.1 逻辑回归分析

逻辑回归(Logistic Regression)分析是一种重要的应用回归分析方法,主要针对0-1型因变量产生的问题,可用于预测因变量的发生概率,或实现其定性分类[15]。常用的逻辑函数形式为:

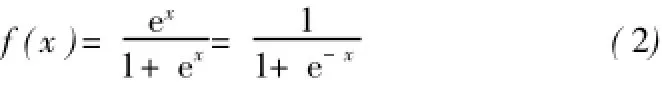
在利用逻辑回归模型预测因变量发生概率时,假设因变量Y是一个二值变量,取值为:

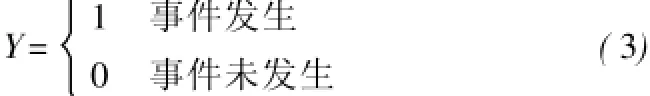
自变量为x1,x2,…,xm,P表示在m个自变量作用下事件发生的概率。

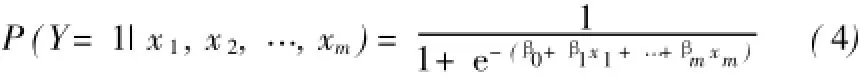
事件发生概率与未发生概率之比的自然对数称为P的logit变换,记作logit(P):

概率P的取值范围在0～1之间,而logit(P)取值没有界限,更适于进行回归分析。令Z=β0+β1x1 +…+βmxm,将复杂的概率预测非线性模型简化为多元线性回归模型。利用样本数据采用最大似然估计法对常数项β0和回归参数β1…βm进行拟合,进而得到P的估计,即:

逻辑回归分析的实质是在线性回归基础上套用了逻辑函数,由于该方法简单、高效,目前已在地质灾害研究领域取得了广泛应用[16,17]。

3.2 模型构建

(1)指标变量选取。物源、水力和地形条件是影响山间滑坡堆积体堵江的主要条件。本文基于中国喜马拉雅山地区堵江滑坡与非堵江滑坡河谷横剖面形态参数的差异分析结果,将不同深度宽深比、凹度、河宽指数、坡高作为地形条件指标;将反映滑坡体物质结构的工程地质岩组、反映滑坡规模的滑坡面积作为物源条件指标;由于滑坡发生时河流的流速、流量等详细水文数据都难以获取,水力条件指标暂用上游流域面积粗略表征。综上,本文共采用7个指标变量参与滑坡体堵江概率预测模型构建(表2)。

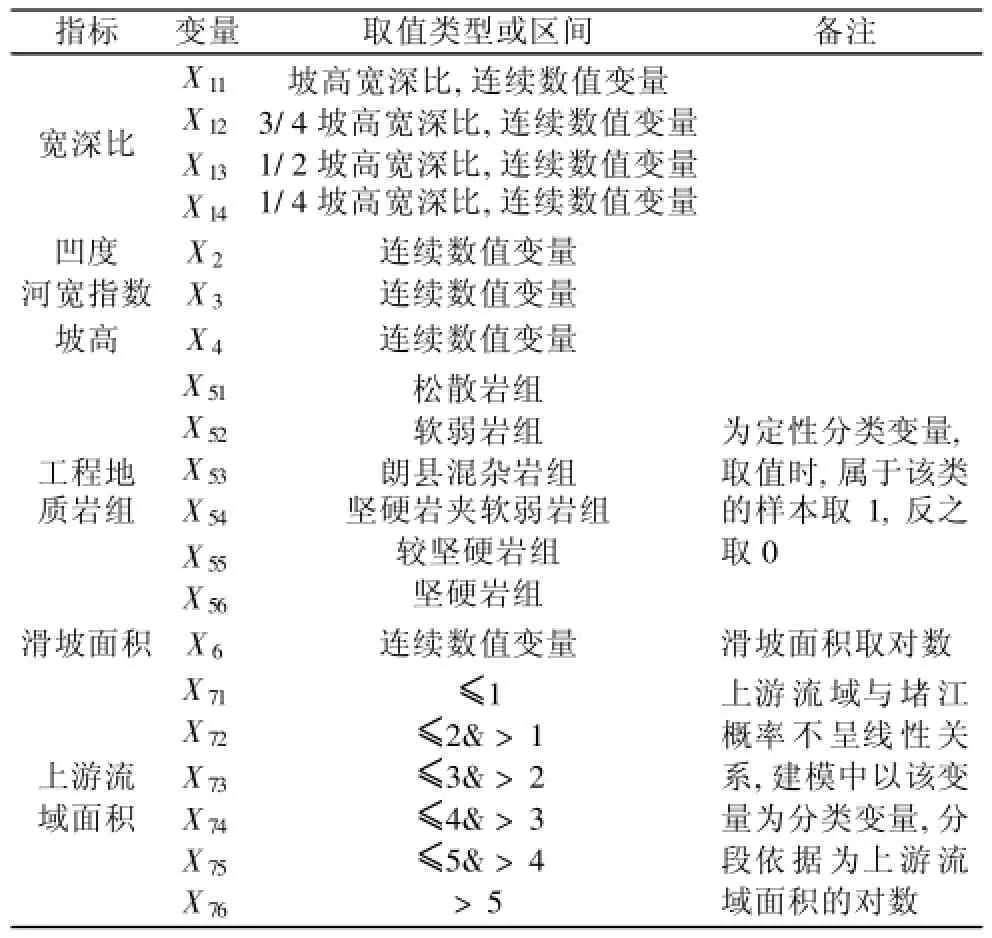
表2 滑坡体堵江预测建模指标变量Table 2 The influence factors of landslide-damning susceptibility modeling

(2)样本数据获取。样本数据质量直接影响模型的精度和可靠性。本文以研究区90个堵江滑坡事件为1-值样本,91个非堵江滑坡点为0-值样本。地形条件指标利用本文编写的河谷横剖面形态参数自动提取程序获取,其他指标利用ArcGIS软件处理分析获取。图4是样本数据获取图。

图4 滑坡体堵江预测建模样本数据获取Fig.4 The way of sample data obtaining

在样本数据中,分别随机选出80个1-值样本和80个0-值样本参与模型构建,留出10个1-值样本和11个0-值样本用于模型验证。利用SPSS统计分析软件的Logistic回归分析工具,设置迭代方式为Forward:Conditional,构建了中国喜马拉雅山地区滑坡体堵江能力评价模型,其表达式为:

经过迭代模型中仅剩坡高宽深比、凹度、河宽指数、工程地质岩组和滑坡面积参与滑坡体堵江概率预测。将上述5个变量代入式(7),就可以对研究区范围内潜在滑坡或新生滑坡体堵江的概率做出预测。当P＞0.5时认为滑坡体堵江易发,反之不易发。各变量的回归系数统计结果见表3。

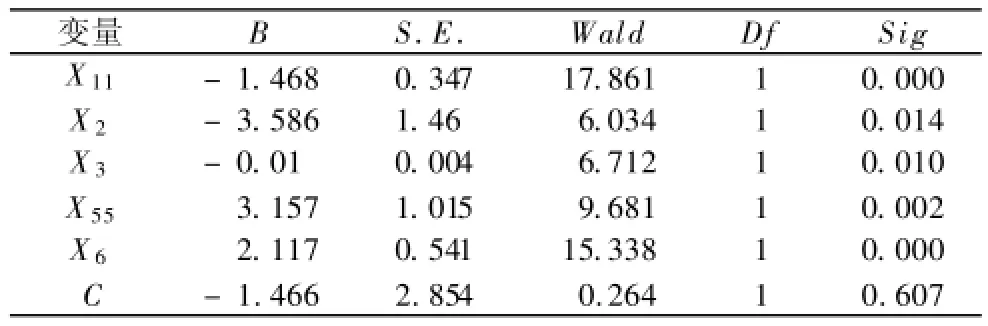
表3 模型参数Table 3 The parameters of prediction model

其中,B是各变量回归系数的估计量,S.E.是Std.Error的缩写,表示回归系数估计量的标准差; Wald是回归系数检验的统计量值(式(8));Df是自由度,Sig是显著性概率。Wald值越大,Sig值越小,说明参数显著性越高。表3中所有回归系数的Wald＞6,Sig＜0.05,说明预测模型在显著性水平0.05条件下是可以接受的。

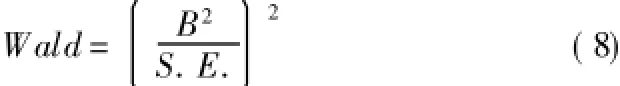
通过中国喜马拉雅山地区滑坡体堵江概率预测模型可以看出,影响该区滑坡体堵江易发性的主要因素包括地形因素以及滑坡体的规模和物质组成,这基本符合工程地质学对滑坡堵江成因的普遍认识。根据回归系数B的取值,坡高宽深比、凹度、河宽指数与滑坡体堵江概率呈负相关关系,滑坡面积与之呈正相关关系,工程地质岩组中的较坚硬岩组是滑坡体堵江形成的有利条件。根据各变量Wald的取值,认为各变量对滑坡体堵江的重要性从高到低排序为坡高宽深比、滑坡面积、工程地质岩组、河宽指数和凹度。水力条件,至少上游流域指标对滑坡体堵江能力的影响并不突出,考虑到现有数据获取和采样水平,认为可以忽略水力条件这一参数。

3.3 模型验证

以P=0.5作为区分滑坡体堵江与否的分类标准,计算并统计了建模样本和验证样本的预测精度,分别见表4、表5。研究区滑坡体堵江概率预测模型对建模样本的总体预测精度为86.25%,其中1-型样本和0-型样本预测精度相差不大;对验证样本的总体预测精度为80.95%,且对1-型样本的预测精度大于0-型样本。可见,该模型对研究区滑坡体堵江的易发性评价较为理想,且评价结果相对保守。

表4 建模样本预测精度Table 4 Prediction accuracy of modeling samples

表5 验证样本预测精度Table 5 Prediction accuracy of verification samples

此外,深入滑坡事件频发且交通相对便利的林芝、米林、朗县、加查、隆子、错那和亚东等县进行实地验证,根据对定位点处相关指标的实地勘查量测和堵江分析结果,认为本文提出的河谷横剖面形态参数能够较好地反映河谷形态特征,而利用研究区滑坡体堵江概率预测模型判断的堵江情况与实际基本相符,证明了堵江预测模型的有效性。

4 结论

本文以物质来源、水力条件和河谷地形为影响因素进行滑坡体堵江概率分析研究和应用。引入坡高、宽深比、剖面面积、凹度、不对称系数和河宽指数等河谷横剖面形态参数,并利用GIS技术基于DEM数据实现了上述参数的自动提取。提取中国喜马拉雅山地区堵江滑坡事件和非堵江滑坡事件样本,统计对比了两类样本河谷横剖面形态特征的差异性,并基于逻辑回归建立了研究区滑坡体堵江概率预测模型,经验证效果较为理想。本文结论如下:

(1)提出的河谷横剖面形态参数及其自动提取方法,具有面向对象、表征全面、提高计算效率和精度等优点,可在河谷地貌研究领域推广应用。

(2)在中国喜马拉雅山地区,堵江滑坡与非堵江滑坡发生处河谷横剖面的坡高、不同深度宽深比、凹度和河宽系数差异显著,其中河宽指数差异最大,3/ 4坡高宽深比次之。相比于滑坡体所在斜坡的平均坡度,上述参数更利于开展滑坡体堵江易发性评价。

(3)基于逻辑回归建立滑坡体堵江概率预测模型是可行的。该方法在中国喜马拉雅山地区的应用精度达到80%以上,且具有评价结果相对保守的特点。各影响因素按照对滑坡体堵江形成的重要性从大到小依次是坡高宽深比、滑坡面积、工程地质岩组、河宽指数和凹度。其中,坡高宽深比、河宽指数、凹度3个地形参数与滑坡体堵江的发生概率呈反相关关系。作为堵江主体,较大的滑坡面积和较坚硬岩组容易导致滑坡堵江事件的形成。

本文是河谷横剖面形态特征分析和滑坡体堵江易发性评价领域的初步尝试,效果比较理想。但所提出的参数计算和模型构建方法还需要应用于更多地区进行验证和完善,这也是下一步的工作方向。

[1] COSTA J E,SCHU ST ER R L.T he formation and failure of nature dams[J].Geological Society of America Bulletin,1988, 100:1054-1068.

[2] SCHU STER R L.Landslide Dams:Processes,Risk and Mitigation[M].Seattle,Washington:American Society of Civil Engineers,1986.

[3] CARRARA A,GUZZETTI F,CARDINALI M,et al.U se of GIS technology in the prediction and monitoring of landslide hazard [J].Natural Hazards,1999,20:117-135.

[4] 石振明,李建可,鹿存亮,等.堰塞湖坝体稳定性研究现状及展望[J].工程地质学报,2010(5):657-663.

[5] DONG J J,TU NG Y H,CHEN C C,et al.Discriminant analysis of the geomorphic characteristics and stability of landslide dams [J].Geomorphology,2009,110(3-4):162-171.

[6] DONG J J,T UNG Y H,CHEN C C,et al.Logistic regression model for predicting the failure probability of a landslide dam [J].Engineering Geology,2011,117(1-2):52-61.

[7] WANG G,LIU F,FU X,et al.Simulation of dam breach development for emerg ency treatment of the Tangjiashan Quake L ake in China[J].Science in China Series E:T echnological Sciences,2009,51(S2):82-94.

[8] SCHU STER R L.Impact of landslide dams on mountain valley [A].EVANS S G.Landslides from Massive Rock Slope Failure [C].Netherlands:Springer,2006.591-616.

[9] 张金山,沈兴菊,谢洪.泥石流堵河影响因素研究——以岷江上游为例[J].灾害学,2007(2):82-86.

[10] 柴贺军,刘汉超,张倬元.滑坡堵江的基本条件[J].地质灾害与环境保护,1996(1):41-46.

[11] ZHOU L,TAKASHI O.DEM analysis on longitudinal and transverse profiles of steep mountainous watersheds[J].Geomorphology,2006,78(1-2):77-89.

[12] ZHOU L,T AKASHI O.Longitudinal and transverse profiles of hilly and mountainous watersheds in Japan[J].Geomorphology,2009,111(1-2):17-26.

[13] 闵石头,王随继.滇西纵向岭谷区河谷形态特征、发育规律及成因[J].山地学报,2007(5):524-533.

[14] 王珊珊,胡瑞林,童立强.中国喜马拉雅山地区滑坡堵江编目及空间特征分析[J].工程地质学报,2015,23(3):361-372.

[15] 何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2011.245-250.

[16] 许冲,徐锡伟.逻辑回归模型在玉树地震滑坡危险性评价中的应用与检验[J].工程地质学报,2012,20(3):326-333.

[17] 刘艺梁,殷坤龙,刘斌.逻辑回归和人工神经网络模型在滑坡灾害空间预测中的应用[J].水文地质工程地质,2010(5):92-96.

Susceptibility Assessment of Landslide-Damming Based on Valley Transverse Profile Morphological Characteristics

WANG Shan-shan,TONG Li-qiang
(ChinaA erogeop hysics and Remote Sensing Center,Beij ing100083,China)

Susceptibility assessment of landslide-damming is a short board in landslide-damming risk research.Taking material source,hydraulic condition and valley topography as main influence factors,the paper analyzed the probability of landslide mass to dam rivers.An automatic extraction method of valley transverse profile morphological parameters was proposed,to quantify valley morphological characteristics.T aking Himalaya of China as the study area,the landslide-damning susceptibility model was built based on logistic regression,and the results were proved to be ideal.The main conclusions are as follows:1)The automatic extraction method of valley transverse profile morphological parameters has the advantages of object-oriented,reflecting comprehensively,high efficient and high-accuracy.2)Comparing the landslides dammed rivers with the landslides un-dammed rivers in Himalaya of China,the valley transverse profile morphological parameters including slope height,width-depth ratio of various depth,valley concavity and river width index have significant differences.Among the above parameters,river width index has the greatest difference,and width-depth ratio of 3/4 slope height takes the second place.3)Susceptibility assessment of landslidedamming based on logistic regression is feasible.The model accuracy applied in Himalaya of China is greater than 80%.T he influenced factors according to the correlation with landslide damming from big to small in proper order are:width-depth ratio of slope height,landslide area,engineering geological petrofabric,river width index and valley concavity.

landslide damming;valley transverse profile;automatic extraction;logistic regression

P642.22

A

1672-0504(2016)05-0097-06

10.3969/j.issn.1672-0504.2016.05.015

2016-03-09;

2016-06-01

王珊珊(1985-),女,工学博士,工程师,研究方向:基于3S技术的地质灾害监测与评价。E-mail:wangss1028@126.com