MAUP效应在城市扩张元胞自动机模拟中的敏感性分析

李 丹,刘小平,罗 勇,王云飞

(1.南阳师范学院环境科学与旅游学院,河南南阳473061;2.中山大学地理科学与规划学院,广东广州510275)

MAUP效应在城市扩张元胞自动机模拟中的敏感性分析

李 丹1,刘小平2*,罗 勇1,王云飞1

(1.南阳师范学院环境科学与旅游学院,河南南阳473061;2.中山大学地理科学与规划学院,广东广州510275)

利用元胞自动机模型进行城市扩张模拟时,其使用的栅格数据格式和基于统计的转换规则提取方法必然会导致可变面积单元问题(the Modifiable Areal U nit Problem,M AU P)的出现。采用系统的敏感性分析方法对该问题的粒度效应、划区效应和综合效应进行了分析,研究表明:1)M AUP问题在CA模拟时是客观存在的,且会对模拟结果造成影响,研究时不能忽视该问题。应进行系统的敏感性分析,获取其对研究问题的影响,寻找适宜的研究粒度和分区方案。2)该研究中粒度效应会呈现明显的尺度阈值,尺度域内的拟合优度和模拟精度较为稳定。尺度阈值在最精细粒度后随即出现,且该阈值与景观指数的尺度阈值一致,反映了景观对象大小对城市扩张模拟的重要影响。3)良好的划区方案能够提高拟合优度和模拟精度,其划区方案应使区域内城市扩张规律差异最小,区域间城市扩张规律差异最大。在大尺度城市扩张模拟时更应采用合理的划区方案以提高模拟精度。4)粒度效应和划区效应的综合影响表现为各区域模型的拟合优度和模拟精度在粒度范围内所受到的影响存在差异,但大多数区域都较为明显地表现出相同的尺度阈值。

元胞自动机;MAUP;城市扩张;粒度效应;划区效应;敏感性分析

0 引言

元胞自动机(Cellular Automata,CA)是由Wolfram提出的空间、时间离散,通过局部规则获得全局涌现特征的动力学模型[1],已被应用于诸多地理格局和过程的建模和模拟,特别是在城市扩张研究中得到了广泛和深入的应用[2-5]。城市扩张研究通常采用遥感影像等栅格数据作为数据源,与CA模型的离散空间具有天然的相似性,同时大多数CA模型的转换规则本质上是通过基于抽样数据的各类统计学方法获取的,因此使用CA模型进行城市扩张模拟时,必然会涉及可变面积单元问题(the Modifiable Areal Unit Problem,MAUP)。MAUP问题被研究者关注的时间较早,其概念由Openshaw提出[6,7],是指面状空间单元的大小和分区方法会对分析结果产生显著的影响,通常涉及两方面的影响:单元大小不同造成的尺度效应(scale effect)和分区方案不同造成的划区效应(zoning effect)。在涉及栅格数据的CA模拟中,建议采用粒度效应替代尺度效应来更好地辨析其概念。MAUP问题已在地理学及其他学科领域证明了其存在性,并得到了广泛关注和研究[8-15]。

尽管研究者一致认识到MAUP问题在地理现象和过程研究中的重要性,但目前还基本没有解决该问题的统一途径或框架,比较好的方法是进行敏感性分析[16-18],定量获取MAUP对研究问题的影响效果,寻找其影响规律和尺度阈值,从而降低MAUP问题造成的影响。在城市扩张CA模拟研究中,研究者对CA模拟涉及的空间(栅格大小)、时间、邻域设置(邻域类型及大小)、转换规则等进行了敏感性分析。如Li等进行了城市扩张模拟中不同转换规则的敏感性分析[19],Wu[20]、Pan[21]、Kocobas[22]、柯新利[23]等进行了元胞大小和邻域设置等因素的敏感性分析,王羊[24]、Kim[25]等进行了空间、时间、概率分布、随机因素的敏感性分析,但以上研究都较少涉及MAUP问题的系统性分析,对于划区效应的关注更少。因此本文拟在城市扩张CA模拟研究中进行全面系统的敏感性分析,定量获取MAUP问题对CA模型造成的影响,辨识可能存在的尺度阈值,并尝试获取降低MAUP问题影响的途径。

1 研究数据及方法

1.1 研究区及数据

选取广东省为研究区域,分别获取了广东省2000年、2005年和2006年的土地利用分类数据和相关空间变量数据。土地利用分类数据为栅格数据,原始空间分辨率为80 m,包括6种用地类型:耕地、林地、草地、水域、城乡建设用地和未利用地。空间变量为归一化距离,包括各栅格单元到城镇中心的距离、到铁路的距离、到高速公路的距离和到公路的距离。采用基于逻辑回归的Logistic-CA模型,首先使用2000年和2005年的土地利用分类数据及空间变量数据获取广东省的城乡建设用地发展规律,然后以2005年土地利用数据作为初始数据,模拟了2005-2006年的城乡建设用地扩展情况,并使用2006年土地利用数据进行模拟精度检验。图1(彩图见封2)和图2为80 m分辨率的土地利用数据、影响因子及模拟结果图。逻辑回归方法基于二分判别,适合获取城市-非城市土地利用类型的转换规则[26,27],使用ROC(Receiver Operating Characteristic)方法评价逻辑回归模型的拟合优度[28],用混淆矩阵和Kappa系数检验模拟的精度[4],其计算方法如下:

设定非城市用地类型栅格为负例,城市用地类型栅格为正例。在模拟结果中,实际为非城市用地类型模拟为非城市用地类型的栅格数量为a,非城市用地类型模拟为城市用地类型的栅格数量为b;城市用地类型模拟为非城市用地类型的栅格数量为c,城市用地类型模拟为城市用地类型的栅格数量为d,则:

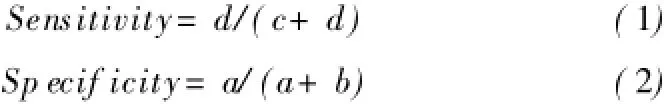
Sensitivity为敏感性或覆盖率,表示正确预测到的正例数在实际正例总数中的比率,在本例中即城市用地模拟精度。Sp ecif icity为负例的覆盖率,表示正确预测到的负例数在实际负例总数中的比率,在本例中即非城市用地模拟精度。通过Sensitivity与1-Specif icity的值可以绘制ROC曲线来评估模拟拟合优度,通常使用AUC(Area Under the ROC Curve,ROC曲线下面积)的值来定量评估,该值越大表示拟合优度越高。

Accuracy为准确率,即预测正确数量占总预测数量的比例,在本例中即模拟的总精度。

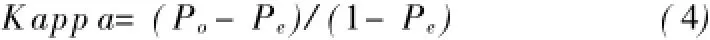
Kappa系数可以反映两者一致性程度的高低,其中Po=(a+d)/(a+b+c+d),为实际一致率,Pe =((a+b)(a+c)+(c+d)(b+d))/(a+b+c+d) (a+b+c+d),表示理论一致率。Kappa系数值越高表示两者一致性程度越高,即模拟结果与真实数据的一致性越高。

图1 广东省80 m分辨率土地利用数据及模拟结果Fig.1 Land use data and simulation result of Guangdong Province at 80 m resolution

图2 广东省80 m分辨率土地利用变化影响因子Fig.2 Land use change impact factors of Guangdong Province at 80 m resolution

1.2 研究方法

对MAUP问题进行系统的敏感性分析,需分别定量评估粒度效应、划区效应和综合效应对逻辑回归模型拟合优度及模拟结果精度所产生的影响。

(1)对于粒度效应的影响,采用栅格重采样(Resample)的方法获取多个空间粒度,具体是将原始80 m分辨率的数据按照整数倍依次重采样为160 m、240 m、320 m、400 m、480 m、560 m、640 m、720 m、800 m、880 m、960 m和1 040 m,共13种空间粒度,分别进行全广东省模型的拟合和模拟。

(2)对于划区效应,主要是比较不同划区方案所产生的影响,并寻找进行最优划区的途径。城市用地扩张是由各驱动力因素共同作用引起的,因此可根据驱动力因素的异同进行分区的划定,使同一分区内驱动力因素的差异最小,不同分区间驱动力因素的差异最大。对于城市扩张影响较大的驱动力因素为经济因素,通常以行政区为数据统计单元,由于其较难进行准确的空间化,因此可将行政区作为分区划定的基本单元,根据经济因素的差异将所有行政区划定出多种划区方案,进行方案之间的对比。研究以广东省各市级行政区为基本统计单元,通过统计年鉴收集了各市级行政区2000-2005年间的人口、经济发展、财政状况、人民生活水平等相关数据,采用聚类分析的方法对21个市级行政区进行了分类划分,以分类结果作为分区划分的依据,产生不同的分区方案。基于分区方案,根据粒度效应分析结果,在160 m粒度下分别进行各分区模型的构建及模拟,随后进行不同划区方案之间的横向比较。

(3)在进行综合效应影响研究时选取相同的粒度范围和其中一种划区方案,分别构建了各粒度下所有分区和全广东省的城市用地扩张模型并进行模拟,然后将各粒度对广东省模型的模拟结果按照各分区的空间范围进行裁切,比较分区模型的模拟精度与整体模型中相应空间范围的模拟精度。

2 研究结果

2.1 粒度效应的敏感性分析

图3为各空间粒度下逻辑回归模型的ROC值统计图,显示在80～1 040 m的空间粒度范围内ROC值的总体差异较小,但也存在2个尺度阈值,分别是160 m和640 m粒度。根据尺度阈值可将整个尺度范围分为3个尺度域,分别是80～160 m、160～640 m和640～1 040 m,尺度域内空间粒度的ROC值差异较小,表明其模拟拟合度较为接近。同时160 m尺度阈值附近的ROC值差异比640 m尺度阈值附近的差异大。ROC值最高的空间粒度为640 m,值为0.676,可以认为该粒度下逻辑回归模型的拟合度最高。ROC值最低空间粒度为80 m,值为0.658。

在各空间粒度下进行了广东省城市用地扩张的模拟,并计算了模拟结果的精度。图4分别列出了各粒度下Logistic-CA模拟的城市用地精度、非城市用地精度、总精度和Kappa系数变化情况。结果显示,各空间粒度下城市用地的模拟精度都达到了93%左右,非城市用地的模拟精度和模拟总精度都达到了99%以上,Kappa系数都达到了0.924以上,说明各空间粒度下的城市用地扩张模拟都能达到很高的模拟精度。其原因一是2005年广东省城市用地面积占陆地总面积的6.95%,其余为非城市用地,使式(1)和式(2)中的a和d值较大;二是因为2005-2006年城市用地转换量为2005年城市用地的6.54%,发生转换的栅格数量较少,同时Logistic-CA模型较好地模拟了城市扩张过程,产生了少量的类型错分栅格,从而使式(1)和式(2)中的b和c值较小。而160 m的空间粒度同样为城市用地模拟精度和Kappa系数变化的尺度阈值,其他粒度下并未出现尺度阈值。

图3 各空间粒度下的ROC值Fig.3 ROC values in all grains

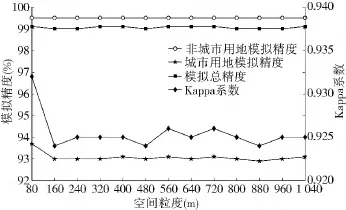
图4 各空间粒度下的模拟精度和Kappa系数Fig.4 Simulation accuracies and Kappa coefficient values in all grains

Goodchild等认为在分析MAUP问题影响时必须考虑地理现象的自然属性特征[18],M nard等在进行空间粒度对土地利用变化模拟结果的敏感性分析研究时,也认为选取合适的空间粒度需要考虑其与景观对象大小的关系[29]。因此本研究从景观格局的形状复杂性、分维数、多样性和均匀性等角度,选择了景观水平的平均形状指数(SHAPE_MN)、平均分维数指数(FRAC_MN)、周长—面积分维数指数(PAFRAC)、Shannon多样性指数(SHDI)和Shannon均匀度指数(SHEI)共5个指标,通过计算各空间粒度下广东省2000年和2005年土地利用分类数据的景观指数以获取其景观特征,分析粒度效应对景观指数的影响,结果分别如图5和图6所示。

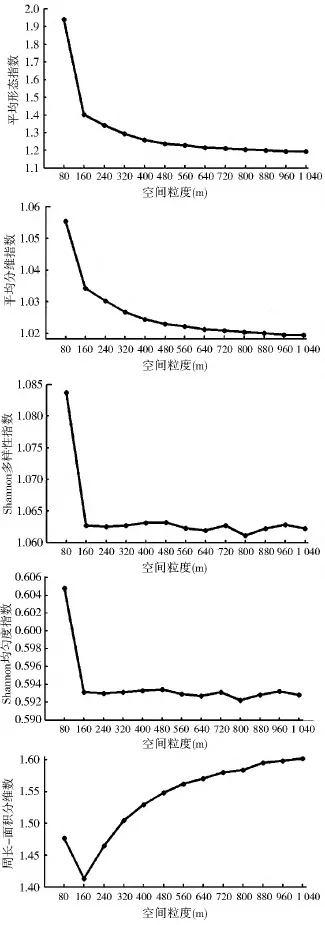
图5 广东省2000年土地利用分类数据各景观指数的粒度效应Fig.5 Scale effect of landscape indexes from land use data of Guangdong Province in 2000

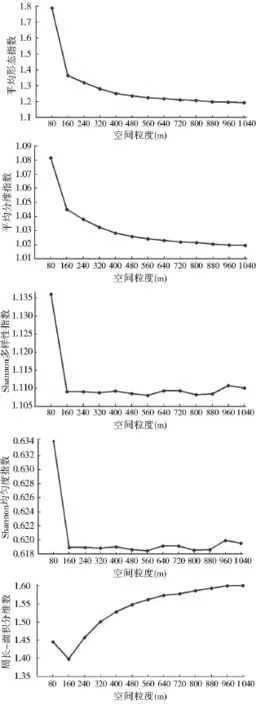
图6 广东省2005年土地利用分类数据各景观指数的粒度效应Fig.6 Scale effect of landscape indexes from land use data of Guangdong Province in 2005

可以发现,从80 m粒度到160 m粒度,各景观指数值均发生了显著的变化,之后的空间粒度下各景观指数值或基本一致,或保持相同的变化趋势。从80 m到160 m,平均形状指数所表示的景观形状复杂程度显著降低,同时景观的多样性和均匀度也显著下降,而160 m之后的粒度范围内各指数值基本保持一致。平均分维数指数和周长—面积分维数可以表现景观的分形特征,80 m到160 m的分维数指数明显降低,而160～1 040 m的粒度范围内,分维数指数的变化趋势趋向一致。有研究者认为,如果分维数随着尺度而改变,则变化趋势的转折点可能指示了景观具有等级结构[30,31]。可见160 m粒度是该景观格局特征变化的重要转折点,这与之前城市用地扩张模拟时出现的160 m尺度阈值是一致的。

2.2 划区效应的敏感性分析

研究根据广东省各市级行政区2000年和2005年的社会经济数据,使用分层聚类的方法在SPSS中对21个市级行政区进行了聚类分析,分层聚类结果如图7、图8所示。两个年份的聚类结果基本一致,根据各类别间的相对距离可以将21个市级行政区分为5个类别,如果进行更为粗略的划分,可以对上述5个类别合并为3个类别,从而分别对应五分区和三分区两种划区方案。

图7 广东省各市级行政区2000年社会经济数据聚类结果Fig.7 Clustering result of all cities in Guangdong Province based on socio-economic data in 2000

图8 广东省各市级行政区2005年社会经济数据聚类结果Fig.8 Clustering result of all cities in Guangdong Province based on socio-economic data in 2005

图9 (彩图见封2)为广东省在2006年两种不同分区方案下的模拟结果。表1为将广东省划分为3个分区时各模型的拟合优度和模拟精度,以及分区模型与全省整体相关指标的比较。可见各分区模型的拟合优度、模拟精度和Kappa系数与全省模型中相应分区范围的结果均存在差异。除分区二的城市用地模拟精度小于全省模型相应分区范围的结果外,分区二和分区三的其它模拟精度及Kappa系数均大于全省模型相应分区范围的结果,说明通过划区方案分区后,分区二模型和分区三模型在模拟对应分区范围的城市用地扩张过程时能获得比整体模型更好的模拟效果。而分区一的非城市用地模拟精度、模拟总精度和Kappa系数均小于全省模型中分区一的结果,表明可能需要寻找更适合该区域土地利用变化特征的分区方案。

图9 广东省两种不同分区方案的模拟结果Fig.9 Simulation results of two different zoning schemes of Guangdong Province in 2006

表2为将广东省划分为5个分区时各模型的拟合优度和模拟精度,以及分区模型与全省相关指标的比较。可以看出,与三分区方案相比,将三分区方案中的分区一划分为更细的两个分区后(五分区方案中的分区一和分区二),对五分区方案中分区一范围的模拟也能获得比整体模型模拟更好的效果。

由表1和表2可以看出,不同的划区方案对城市用地扩张模型的拟合优度和模拟精度的影响是不同的。通过划区方案的划分,某些分区模型的模拟结果比在整体模型模拟时对应分区范围的结果具有更高的模拟精度。这说明在相同驱动力因子作用下,这些分区模型能够更好地拟合该分区的城市用地扩张规律,因此模拟精度优于整体模型中相应分区范围的模拟精度,因此需要寻找最优的划区方案,来准确地拟合和模拟每个分区的城市用地扩张过程。有研究者认为划区效应在随机分布的情况下影响不大,而在具有明显空间模式的情况下影响较大[16],因此可考虑利用空间加权回归等方法获取研究地域的空间模式特征后再采用合适的分区方法[32]。

2.3 粒度效应和划区效应共同作用的敏感性分析

主要探讨MAUP问题中的粒度效应和划区效应对土地利用变化模拟的共同影响,方法为采用三分区方案在所有粒度下分别进行各分区和广东省模型的模拟。图10-图14为得到的ROC值、各模拟精度和Kappa系数统计图。

从图10-图14可以看出,3个分区模型和广东省模型的拟合优度和模拟精度都受到粒度效应的影响,但呈现出不同的影响特征。其中分区二和分区三的影响特征与广东省的影响特征较为一致,而分区一的影响特征与其他区域较为不同,表明划区后不同区域所受到的粒度效应影响是不同的。粒度效应对各区域拟合优度的影响程度较大,且无明显的规律性。而160 m粒度同样可以被认为是对大多数区域模型拟合优度和模拟精度影响较大的尺度阈值。

表1 广东省三分区方案模型拟合优度与模拟精度统计Table 1 Goodness of fit and simulation accuracy of a 3-partitions zoning scheme of Guangdong Province

表2 广东省五分区方案模型拟合优度与模拟精度统计Table 2 Goodness of fit and simulation accuracy of a 5-partitions zoning scheme of Guangdong Province

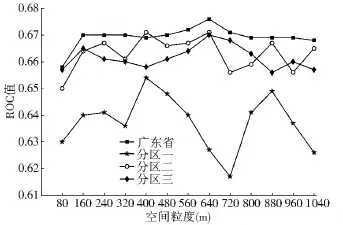
图10 各空间粒度下3个分区及广东省的ROC值统计Fig.10 ROCvalues of 3 partitions and the whole Guangdong Province in all grains

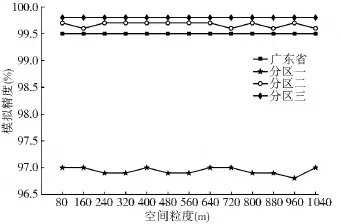
图11 各空间粒度下3个分区及广东省的非城市用地模拟精度统计Fig.11 Simulation accuracy of non-urban land of 3 partitions and the whole Guangdong Province in all grains

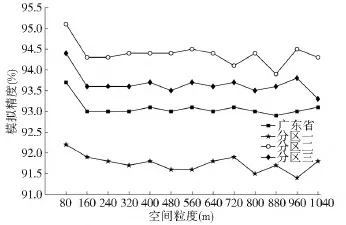
图12 各空间粒度下3个分区及广东省的城市用地模拟精度统计Fig.12 Simulation accuracy of urban land of 3 partitions and the whole Guangdong Province in all grains

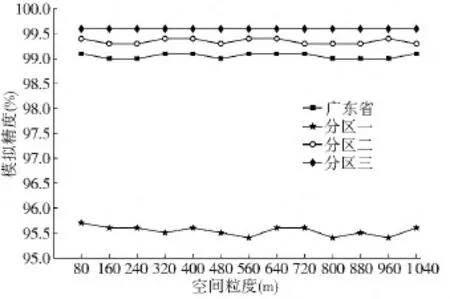
图13 各空间粒度下3个分区及广东省的模拟总精度统计Fig.13 Overall simulation accuracy of 3 partitions and the whole Guangdong Province in all grains

图14 各空间粒度下3个分区及广东省的Kappa系数统计Fig.14 Kappa index values of 3 partitions and the whole Guangdong Province in all grains

3 结论

通过系统的敏感性分析途径,本研究详细分析了利用CA模型进行城市扩张模拟时MAUP问题所带来的影响。研究认为:1)MAUP问题的粒度效应和划区效应在CA模拟时是客观存在的,且会对模拟结果造成影响,因此研究时不能忽视MAUP问题。2)粒度效应会呈现明显的尺度阈值,尺度域内的拟合优度和模拟精度较为一致。本研究中逻辑回归模型的拟合优度和模拟精度的尺度阈值均在最精细粒度后随即出现。而该阈值与景观指数的尺度阈值一致,反映了景观对象大小对城市扩张模拟的重要影响。3)不同划区方案产生的划区效应会对模型拟合优度和模拟精度产生影响,良好的划区方案能够提高拟合优度和模拟精度,划区方案应使区域内城市扩张规律差异最小,区域间城市扩张规律差异最大。在大尺度城市扩张模拟中更应选择合理的划区方案以提高模拟精度。4)粒度和划区的综合效应表现为各区域模型的拟合优度和模拟精度在粒度范围内所受到的影响存在差异,但大多数区域较为明显地表现出相同的尺度阈值。5)目前对于MAUP问题尚无统一的解决框架,但由于其作用不可忽视,因此应在得出研究结论用于空间决策前进行系统的敏感性分析,获取其对研究问题的影响,辨识尺度阈值,找到合适的研究粒度和分区方案。6)今后的研究还应进行涉及更多地域及数据源的MAUP效应分析,寻找MAUP问题对城市扩张CA模拟的一般规律,同时引入启发式的多因素分区方法,获取更好的分区方案。

[1] WOL FRAM S.Cellular automata as models of complexity[J]. Nature,1984,311(5985):419-424.

[2] LI X,YEH A G.Modelling sustainable urban development by the integration of constrained cellular automata and GIS[J].International Journal of Geographical Information Science,2000, 14(2):131-152.

[3] LI X,YEH A G.Neural-network-based cellular automata for simulating multiple land use changes using GIS[J].International Journal of Geographical Information Science,2002,16(4):323-343.

[4] 黎夏,叶嘉安,刘小平,等.地理模拟系统:元胞自动机与多智能体[M].北京:科学出版社,2007.

[5] LIU X,L I X,SHI X,et al.Simulating complex urban development using kernel-based non-linear cellular automata[J].Ecological modelling,2008,211(1):169-181.

[6] OPENSHAW S,T AYLOR P J.A million or so correlation coefficients:T hree experiments on the modifiable areal unit problem [J].Statistical Applications in the Spatial Sciences,1979,21: 127-144.

[7] OPENSHAW S.T he M odifiable Areal Unit Problem[M].Norwich:GeoBooks,1984.

[8] JELINSKI D E,WU J.T he modifiable areal unit problem and implications for landscape ecology[J].Landscape Ecology, 1996,11(3):129-140.

[9] SWIFT A,LIU L,U BER J.Reducing M AUP bias of correlation statistics between water quality and GI illness[J].Computers, Environment and U rban Systems,2008,32(2):134-148.

[10] PARENT EAU M,SAWADA M C.The modifiable areal unitproblem(M AUP)in the relationship between exposure to NO2and respiratory health[J].International Journal of Health Geographics,2011,10(58):1.

[11] M IT RA R,BU LIU NG R N.Built environment correlates of active school transportation:neighborhood and the modifiable areal unit problem[J].Journal of Transport Geography,2012, 20(1):51-61.

[12] XU P,HU ANG H,DONG N,et al.Sensitivity analy sis in the contex t of regional safety modeling:Identifying and assessing the modifiable areal unit problem[J].Accident Analysis and Prevention,2014,70:110-120.

[13] 邓祥征,战金艳.中国北方农牧交错带土地利用变化驱动力的尺度效应分析[J].地理与地理信息科学,2004,20(3):64-68.

[14] 王岩松,赵永.河南省经济发展的空间相关性及尺度效应[J].地理与地理信息科学,2015,31(5):69-72.

[15] 陈江平,张瑶,余远剑.空间自相关的可塑性面积单元问题效应[J].地理学报,2011,66(12):1597-1606.

[16] FOTHERINGHAM A S,ROGERSON P A.The SAGE Handbook of Spatial Analysis[M].Sage,2008.

[17] FOT HERINGHAM A S,BRU NSDON C,CHARLTON M. Quantitative Geography:Perspectives on Spatial Data Analysis [M].Sage,2000.

[18] GOODCHILD M F,QUA TT ROCHI D A.Scale,multiscaling, remote sensing,and GIS[A].GOODCHILD M F,QUATTROCHI D A.Scale in remote sensing and GIS[C].Boca Raton,FL:CRC Press,1997.406,2004-2009.

[19] LI X,LIU X,YU L.A systematic sensitivity analysis of constrained cellular automata model for urban growth simulation based on different transition rules[J].International Journal of Geographical Information Science,2014,28(7):1317-1335.

[20] WU H,ZHOU L,CHI X,et al.Quantifying and analyzing neighborhood configuration characteristics to cellular automata for land use simulation considering data source error[J].Earth Science Informatics,2012,5(2):77-86.

[21] PAN Y,ROT H A,YU Z,et al.T he impact of variation in scale on the behavior of a cellular automata used for land use change modeling[J].Computers,Environment and Urban Sy stems, 2010,34(5):400-408.

[22] KOCABAS V,DRAGICEVIC S.Assessing cellular automata model behaviour using a sensitivity analysis approach[J]. Computers,Environment and Urban Sy stems,2006,30(6): 921-953.

[23] 柯新利,邓祥征,何书金.地理元胞自动机模型的尺度敏感性及原因[J].地理研究,2010,29(5):863-872.

[24] 王羊,高阳,赵琳,等.元胞自动机模型的尺度敏感性分析[J].北京大学学报(自然科学版),2011,47(4):750-758.

[25] KIM J H.Spatiotemporal scale dependency and other sensitivities in dynamic land-use change simulations.[J].International Journal of Geographical Information Science,2013,27(9): 1782-1803.

[26] WU F.Calibration of stochastic cellular automata:T he application to rural-urban land conversions[J].International Journal of Geographical Information Science,2002,16(8):795-818.

[27] 李丹,黎夏,刘小平,等.GPU-CA模型及大尺度土地利用变化模拟[J].科学通报,2012,57(11):959-969.

[28] PONTIU S R G,SCHNEIDER L C.Land-cover change model validation by an ROC method for the Ipswich watershed,M assachusetts,USA[J].Ag riculture,Ecosystems&Environment,2001,85(1):239-248.

[29] MÉ NARD A,M ARCEAU D J.Exploration of spatial scale sensitivity in g eographic cellular automata[J].Environment and Planning B:Planning and Design,2005,32(5):693-714.

[30] SUGIHARA G,MAY R M.Applications of fractals in ecology [J].T rends in Ecology&Evolution,1990,5(3):79-86.

[31] LAM N S,QUAT T ROCHI D A.On the issues of scale,resolution,and fractal analysis in the mapping sciences[J].T he Professional Geographer,1992,44(1):88-98.

[32] FOT HERINGHAM A S,BRUNSDON C,CHARL TON M. Geographically Weighted Regression:T he Analysis of Spatially Varying Relationships[M].John Wiley&Sons,2003.

Sensitivity Analysis of the Modifiable Areal Unit Problem(MAUP)in Simulating Urban Expansion Dynamic Using Cellular Automata

LI Dan1,LIU Xiao-ping2,LUO Yong1,WANG Yun-fei1
(1.College of Environmental Science and Tourism,N anyang Normal University,Nanyang 473061; 2.School of Geograp hy and Planning,Sun Yat-Sen University,Guangz hou510275,China)

When using cellular automata as a simulation model of urban expansion,the raster data format and the extraction of conversion rules based on statistical methods will inevitably lead to the MAUP(the Modifiable Areal Unit Problem).A systematic sensitivity analysis has been used to get the scale effect,zoning effect and combined effect on simulation results.The results show that:1)The MAUP in CA model simulation is an objective reality,the simulation results will be affected,and it cannot be ignored.Systematic sensitivity analysis should be carried out to get its impact on the research questions and find the proper grain and partition scheme.2)T he scale effect shows a significant scale threshold,goodness of fit and simulation accuracy is stable along the scale domain.Scale threshold appears after the finest grain,and is consistent with the scale threshold of the landscape. This reflects an important insight that the urban sprawl process is related to the size of landscape objects.3)Better zoning scheme can improve the goodness of fit and simulation accuracy,and the zoning plan should have minimal differences on rules of urban expansion within the region,and the largest differences among the regions.This is an essential problem that should be considered in large-scale urban expansion simulations.4)The combined effect shows different effects on different regions,but there are the same scale threshold for most regions.

cellular automata;M AU P;urban expansion;scale effect;zoning effect;sensitivity analysis

F291.1

A

1672-0504(2016)05-0014-08

10.3969/j.issn.1672-0504.2016.05.003

2016-07-15;

2016-08-15

国家自然科学基金青年科学基金项目(41301443)

李丹(1980-),男,博士,讲师,主要从事地理模拟、高性能地理计算等研究。*通讯作者E-mail:liux p3@mail.sysu.edu.cn