基于空间自回归CA模型的城市土地利用变化模拟与预测

冯永玖,杨倩倩,崔 丽,刘 艳

(1.上海海洋大学海洋科学学院,上海201306;2.大洋渔业资源可持续开发教育部重点实验室,上海201306; 3.昆士兰大学地理、规划与环境管理学院,布里斯班,澳大利亚4072)

基于空间自回归CA模型的城市土地利用变化模拟与预测

冯永玖1,2,杨倩倩1,崔 丽1,刘 艳3

(1.上海海洋大学海洋科学学院,上海201306;2.大洋渔业资源可持续开发教育部重点实验室,上海201306; 3.昆士兰大学地理、规划与环境管理学院,布里斯班,澳大利亚4072)

该文构建了一种基于空间自回归的地理元胞自动机(CA)模型——SARCA模型,该模型能够较好融合地理系统模拟中的空间自相关特性,且获取的CA参数具有明确的物理意义。以1995-2015年上海城市土地利用为案例,验证了该模型的有效性。CA参数和城市土地转化概率表明,上海市外环线对于CA参数的贡献相比其他空间变量具有压倒性优势,到外环线距离越近则土地发展为城市的概率就越大。将基于Logistic回归的CA模型(LogCA)作为比较对象,模拟同期上海全域城市土地利用变化过程。CA规则表明,SAR在赤池信息量准则(AIC)、残差的描述性统计量和空间自相关指标等方面均优于Logistic回归。同时,SARCA模型在2005年和2015年的土地利用模拟结果总体精度分别为86.3%和82.0%,均优于LogCA模型的模拟结果(总体精度分别为79.8%和76.3%)。

元胞自动机;城市土地利用变化;空间自回归;Logistic回归;上海

0 引言

元胞自动机(Cellular Automata,CA)作为一种认识系统复杂性的方法,由简单的同质个体组成,协同作用之后具有复杂的行为。CA包含4个基本要素:元胞、状态、邻居及转换规则。1970年,T obler首次利用CA模型模拟美国底特律地区的城市扩展,并强调地理模型的核心特征是局部环境因子(邻域影响)[1]。此后,CA被广泛用于模拟地理复杂系统及其动态演变过程,尤其是城市扩展和土地利用变化[2]。有关CA的国内外文献非常丰富,涉及转换规则定义、元胞邻域影响、空间尺度影响、模型评价、案例应用、精度评定等[3-11]。转换规则是CA建模的核心和难点,也是地理系统模拟科学问题之所在[12],直接决定CA模型的特征并影响其模拟性能。

转换规则的获取方法很多,本文将这些方法简单地归纳为2类:显性规则和隐性规则。显性规则指CA参数可以类比为驱动因素的权重或规则,具有明确的物理意义,通过权重能够清晰评定每一个变量对土地利用变化的贡献,如Logistic回归[13];隐性规则指构建CA规则的参数没有明确的物理意义,如神经网络[14]。除了Logistic回归,显性规则还包括主成分分析[15]、偏最小二乘回归[16]、核方法[17,18]、粗集[19]、模糊集[20]和案例推理[21]等;也包括全局最优化方法,如遗传算法[22]、粒子群算法[23]和模拟退火算法[24]等。除了神经网络,隐性规则还包括蚁群智能[25,26]、免疫智能[27,28]、支持向量机[29,30]、系统动力学[31]、CA-Markov模型[32]等。国内外文献中涉及的CA模型远不止上述所列,成功地应用在国内外不同区域,且各有其优势与适用性,实质性地推动了CA理论与应用的发展。

空间实体之间存在空间自相关特性,土地利用与城市格局也不例外。地理学第一定律表明,相邻的地理实体有较高的相似性,距离较远的实体相似性较小[33]。这意味着土地利用在空间上可能存在聚类簇,在这些聚类簇内土地利用与空间变量之间的关系是高度相似的[34]。因此,构建CA模型时如果考虑空间自相关因素,所建立的模型则能很好地体现相关性及距离因素的影响。另一方面,目前一些CA模型由于没有考虑空间自相关,拟合模型的残差分布并不是随机的,其空间自相关统计量和z得分均较高,即残差中存在空间聚类簇,这一定程度上限制了CA模型的模拟效果和精度。空间自回归(Spatial Autoregressive,SAR)模型是一种考虑空间自相关特性的空间统计学方法[35],在土地利用变化分析中已经得到应用[34],将其用于CA规则的获取能够使建立的模型融合空间自相关特性。本文利用SAR在建模中将空间自相关统计量作为一项指标加入,提出了一种基于SAR的地理CA模型(SARCA)。SARCA模型被用于模拟上海市全域1995-2015年土地利用变化,从而检测其有效性并考量近20年上海城市扩展过程。为检测SARCA模型的性能,利用Logistic回归建立CA模型(LogCA)并模拟同时期上海市土地利用变化,在规则拟合精度及模拟结果方面与SARCA模型进行比较。

1 数据与方法

1.1 研究区域

上海市地处中国南北海岸中心点,长江和黄浦江入海汇合处,西接江苏和浙江两省。2010年上海市下辖17区1县,其中黄浦、卢湾、静安、长宁、徐汇、虹口、普陀、闸北、杨浦9区为中心区(图1a),约占上海全域面积的2.3%;遥感数据显示,上海全域总面积为6 885 km2。作为长江三角洲的龙头城市, 1995年以来上海市进入快速城市化时期,遥感数据显示其城市建成区面积从1995年的822 km2增加到2015年的2 429 km2。上海郊区城市化程度同样非常高,郊区与城市中心区没有显著的分界线,因此上海市是检测SARCA模型可用性和效果的理想区域。利用1995年和2005年的Landsat-5 T M影像,以及2015年的Landsat-8 OLI影像作为基础数据,分别解译了3期土地利用格局,并以1995年作为CA模拟的初始年份(图1b)。以30 m空间分辨率获取空间变量并进行CA模拟。

图1 研究区域及1995年土地利用分类Fig.1 Study area and its land use pattern in 1995

1.2 空间变量

土地利用转化受自然地理属性、社会经济和限制条件等多重因素的影响[27]。自然地理属性指高程、坡度和土质等,社会经济指对土地利用影响重大的经济、人口、政策等,限制因素则指限制土地元胞发生状态改变的条件,如可开发总量、基本农田、生态保护区、特殊用地等[7,21]。一些因素对土地元胞从非城市向城市转变产生推力作用,如城市道路、公路、铁路、居住区、工业区等[35,36];一些因素则产生阻力作用,如基本农田、生态保护区、特殊用地等[13]。根据研究区域的具体情况,常以到市中心的距离(Durban)、到区中心的距离(Ddistrict)、到主干道路的距离(Droads)、到农用地的距离(Dagri)作为空间距离变量(表1)。对于本研究区,中环线和外环线对上海市城市发展的影响非常重大,因此将其作为影响因素单独列出,分别获得到中环线的距离(Dmidring)和到外环线的距离(Doutring)。上海地区非常平坦,在地形上城市土地利用未受到影响[37],因此高程或坡度不在考虑范围内。利用系统抽样方法(Systematic Sampling)对每1 km2网格抽取一个点,获取各空间变量的值、土地利用初始年份(1995年)和结束年份(2005年)状态值,上海全域共获得6 701个有效样本点用于训练CA转换规则。

1.3 空间自回归CA模型

CA定义任意元胞i在时刻t+1的状态由其在时刻t的状态和元胞邻域决定[3,4],非城市(Non-urban)元胞转化为城市(Urban)元胞的全局概率Pgi,t可表达为:

表1 用于测算土地转变概率的空间变量

Table 1 Spatial variables used to compute land conversion probability

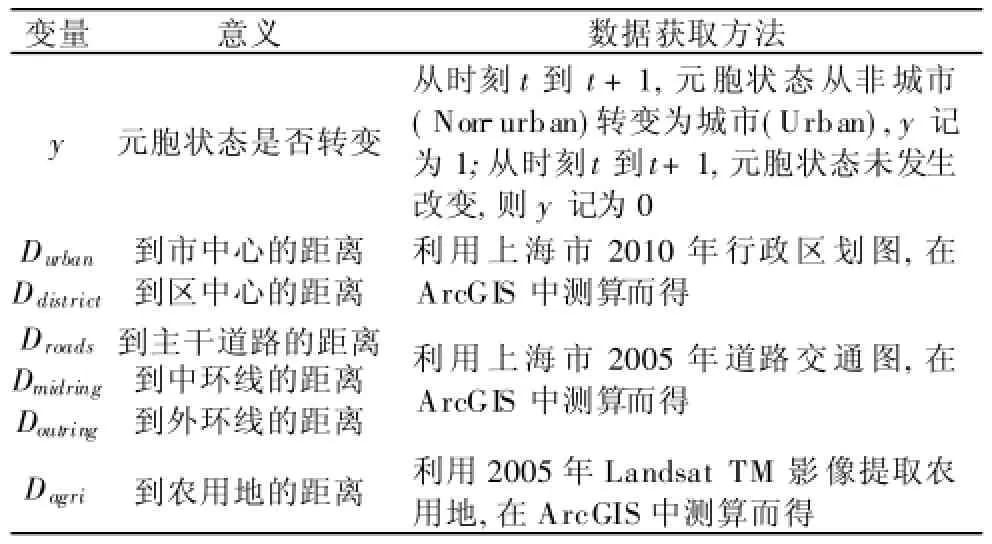
变量意义数据获取方法y元胞状态是否转变从时刻t到t+1,元胞状态从非城市(Non-urban)转变为城市(Urban),y记为1;从时刻t到t+1,元胞状态未发生改变,则y记为0 Durban Ddistrict到市中心的距离到区中心的距离利用上海市2010年行政区划图,在ArcGIS中测算而得Droads Dmidring Doutring利用上海市2005年道路交通图,在ArcGIS中测算而得Dagri到农用地的距离利用2005年Landsat TM影像提取农用地,在ArcGIS中测算而得到主干道路的距离到中环线的距离到外环线的距离

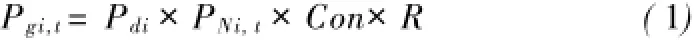
式中:Pdi是由空间变量决定的土地利用转化概率, PNi,t是半径为N的邻域影响,Con是限制因素,R是随机因素。

(《庚辰六月晦，立秋，刘青园师陆招，偕何玉民田季，高陪左田师纳凉崇效寺，重展《青松红杏画》卷次左田师韵》)

Pdi较其他3项复杂,所以下文先讨论其他3项再对Pdi进行详细说明。对于邻域影响的评估,CA模型多采用正方形或圆形的规则邻域,如m×m的Moore邻域可以表达为:

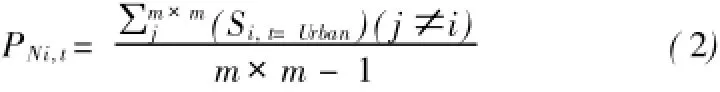
限制因素Con表示元胞受到某种限制而不能发展并转化为城市元胞,这种因素包括大面积水体、基本农田、生态保护区以及公园和绿地等[25,37]。Con可以表达为:

通过式(2)-式(8)得到式(1)等式右侧的4项,即可测算元胞i的全局转化概率Pgi,t。在实际计算中,Logistic回归用R语言(RGui)实现[38],SAR则用GeoDa实现[39]。测算得到元胞全局转换概率Pgi,t之后,与设定的阈值Pthd(其值在0～1之间)进行比较,以确定元胞i在下一时刻的状态是否发生转变。当元胞i的转换概率Pgi,t大于设定阈值Pthd时,转化为城市类型,否则元胞保持状态不变:

式中:Con取值0或1,0表示该元胞不可以发展为城市元胞,1表示可以发展为城市元胞。

随机因素R用于模拟不确定因素导致的元胞状态转变,如某元胞在附近没有城市元胞的状态下通过随机因素提高发展概率,从非城市状态转化为城市状态[3,4,29]。随机因素R表达为:

式中:r是0～1间的随机数,α是随机因素R的控制参数,取值是0～10间的整数。

空间变量决定的转化概率Pdi是转换规则的核心部分,它代表了这些因素对土地利用的影响,并通过概率的方式影响下一时刻的元胞状态。概率Pdi可表达为:

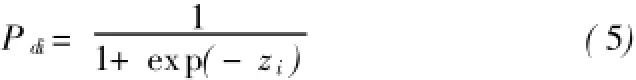
式中:a0是常数,aj(j=1,2,…,k)是CA转换规则的参数,亦即空间变量xj(j=1,2,…,k)的权重。如果利用空间自回归(SAR)获取CA参数,则zi可以表达为[33,35]:

式中:W是被解释变量zi的标准化空间权重矩阵,ρ是空间滞后Wzi的参数,X=(xi,…,xk)是向量形式的空间变量,β是空间变量X的参数向量,即空间变量的权重向量,其意义等同于式(6)中的aj(j=0, 1,…,k),σ2和In分别是残差项ε的方差和空间自相关系数[33,35]。

空间权重矩阵是各个像元在不同位置空间独立性的参数化表示。本文基于空间邻接关系定义空间权重W,具体地采用1阶Q邻接(Queen Contiguity)权重矩阵[33]。权重矩阵中的每一个元素表达为:

1.4 转换规则及模拟精度评价

本文采用赤池信息准则(Akaike Information Criterion,AIC)、残差描述性统计和残差空间自相关评价转换规则[38,39]。AIC是衡量统计模型拟合优良性的一种标准,AIC值越小表明所建立的模型结果越好。模型拟合的残差是评价模型优良的另一种标准,良好的模型其残差项的平均值应接近于0、而残差平方和应尽量小;此外,优良模型的残差应为随机分布,因此其空间自相关统计量应指示其不具有空间自相关特性且p值要大,p＞0.05则随机分布成立的可能性较大。RGui和GeoDa都提供了模型拟合的AIC值和残差项的具体数值[35,39],通过GIS软件能够方便地测算残差项的空间自相关统计量,如Moran′s I指数。

通过与遥感分类的土地利用格局进行比较,对模拟结果进行精度计算是CA模型常用的评价方法,主要指标有总体精度(Overall Accuracy)、Kappa系数和景观指数(Landscape Metrics)等[27,40,41]。本文将总体精度分解为城市(Hit)和非城市(Correct Rejection)两类、将错误分解为忽略性(Miss或O-mission)和替代性(False或Commission)两类,利用Pontius方法将错误同时分解为数量错误(Quantity Error)和位置错误(Allocation Error)[42]。忽略性错误指的是实际为城市但模拟为非城市,即CA模型未能捕捉到的城市元胞;替代性错误指的是实际为非城市但模拟为城市,即CA模拟错误地增加的城市元胞。

2 结果与分析

2.1 CA转换规则

CA转换规则拟合结果表明,SAR的AIC值(1 872.76)远小于Logistic(3 962.20),这指示SAR能够更好地解释上海市土地利用转换的抽样样本,其拟合效果显著优于Logistic回归(表2)。描述性统计表明,Logistic回归的残差均值较大(0.0205),而SAR的均值为0,且前者的残差平方和远大于后者,指示了SAR具有更合理的残差分布和拟合效果。空间自相关表明,Logistic回归的残差具有一定的空间聚集性,SAR的残差则为显著的随机分布,同样指示了SAR的建模拟合效果优于Logistic回归,因此可以预见SARCA将有更好的模拟结果。

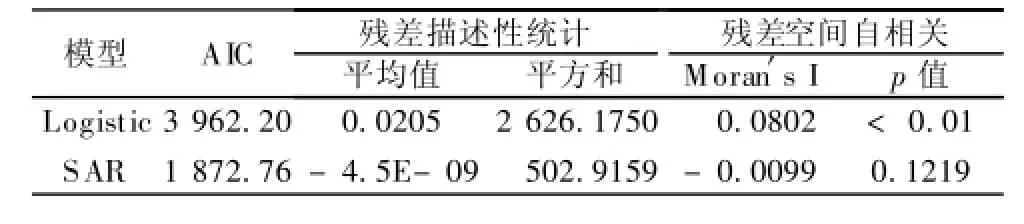
表2 CA转换规则获取的拟合效果Table 2 Fitting performance for the CA transition rules

Logistic回归获取的CA参数表明,影响土地利用变化的因素从强到弱依次为:外环线(Doutring, -5.1619)、道路(Droads,-3.8701)、中环线(Dmidring, -2.9124)和区中心(Ddistrict,-1.2912);SAR获取的参数表明,影响因素从强到弱依次为:外环线(Doutring,-0.3150)、中环线(Dmidring,-0.0654)、区中心(Ddistrict,-0.0544)和道路(Droads,-0.0461)(表3)。由于模型机制的差异性,SAR参数的绝对值显著小于Logistic回归;但两种模型获取的CA参数具有一些相近的特征。对于中小城市,空间距离上越靠近市中心,土地转化为城市类型的概率较大;但对于特大城市则存在相反的情况,即与市中心保持一定距离的区域发展为城市的概率较大,这是因为已有的上海中心区面积较大,而城市发展一般位于城市边缘区,该边缘区到中心区则有一定的距离。两种CA模型的参数均表明,外环线对于CA参数的贡献相比其他空间变量具有压倒性优势,这指示上海城市边缘区在外环线附近,即到外环线距离越近则发展为城市的概率就越大。

表3 用于测算土地转变概率的空间变量Table 3 Spatial variables used to compute land conversion probability

利用已建立的转换规则,获取30 m分辨率下空间变量影响的转化概率Pdi分布(图2),其中Logistic回归的概率值域较宽(0.60～0.92),SAR的概率值域较窄(0.66～0.76),但最小值高于Logistic回归;在与式(1)中的其他因素连乘之后Pgi,t的数值势必降低,因此设置0.52作为元胞转换阈值Pthd。图2清晰地显示,城市中心区和远郊区(青浦、浦东南部和崇明)的发展概率较低;外环线(蓝色环线)内外8 km区域的发展概率大于其他区域,这与表3所示结果一致;上海全域转化概率最高值出现在外环线南北向与东西向的浦东新区交界区域。虽然在总体格局上两个概率图基本一致,但在细节上存在差异,这种差异是CA参数贡献的可视化体现;Logistic的概率图显著带有主干道路的痕迹,即在主干道附近概率值变化较大;SAR概率图的色谱变化更为平滑,表明在局部区域概率值起伏变化的程度低于Logistic回归。

2.2 2005年模拟结果

以1995年城市土地利用格局为初始状态,利用两种CA模型分别运行10次,得到上海市2005年的结果,并将模拟结果与2005年遥感分类结果进行叠加(图3,彩图见封3)。叠加结果包含5类:实际和模拟均为城市(Hit)、实际为非城市模拟为城市(False)、实际为城市模拟为非城市(Miss)、实际和模拟均为非城市(CR)以及水体(Water)。

总体精度显示,LogCA模型为79.8%、SARCA模型为86.3%,SARCA模型高于前者6.5%(表4)。LogCA模型正确模拟百分比中,20.0%来自对城市元胞的正确捕捉,59.8%来自非城市元胞;SARCA模型精度则可以分解为城市21.3%、非城市65.0%。对于模拟结果,两个CA模型最显著的差异出现在浦东新区外环线南北向与东西向交界处。由于在该区域转化概率Pdi的值较大,形成了一定面积的替代性错误模拟元胞,这种错误SARCA (13.6%)显著小于LogCA(18.8%)。对于忽略性错误元胞,由于所占比例较小,目视判别较难从图3中发现,其中LogCA模型为1.4%、SARCA模型为0.1%。通过Pontius方法可知两种模型的数量错误小于位置错误,即CA模型的错误主要是位置差异导致的;与LogCA模型比较,SARCA模型数量和位置错误均较小,表明SARCA模拟效果更好。在不考虑水体的情况下,2005年上海市城市类型土地占22.2%,即任何一种模型城市精度与忽略性错误之和。

图2 空间变量决定的土地利用转化概率Pdi

Fig.2 The land conversion probability Pdidetermined by the spatial variables

图3 LogCA和SARCA两种模型下2005年的模拟结果Fig.3 Simulation results in 2005 using LogCA and SARCA models

表4 2005年两种模型的模拟精度Table 4 Simulation accuracies of the two CA models in 2005

2.3 2015年预测结果

以2005年模拟结果为初始状态,利用已建立的转换规则经过10次循环执行,得到2015年上海市城市土地利用预测结果,并将该结果与2015年遥感分类结果叠加(图4,彩图见封3)。在总体格局上,LogCA与SARCA预测结果较为接近,其中忽略性错误的元胞虽然比例较小,但可通过目视清晰辨识。2015年城市土地类型占总面积的35.2%,相比2005年增长了13%;土地类型从非城市向城市转变主要发生在外环线以外,而对于远郊区尤其是崇明县,土地利用变化并不剧烈。

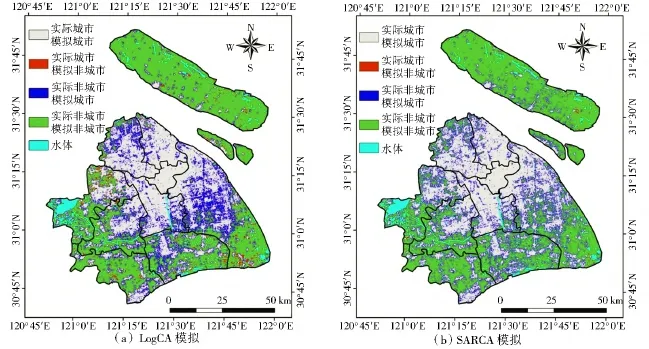
图4 LogCA和SARCA两种模型下2015年的预测结果Fig.4 Prediction results in 2015 using LogCA and SARCA models

两个CA模型的总体精度分别为LogCA 76.3%、SARCA 82.0%,表明SARCA高于LogCA 5.7%(表5);两者的精度均低于2005年,说明模拟精度随时间呈衰减趋势。LogCA模型正确模拟百分比中,33.3%来自对城市元胞的正确捕捉,43.0%来自非城市元胞;SARCA模型精度则可以分解为34.9%城市、47.1%非城市。LogCA和SARCA模型没有捕捉到的城市元胞分别占1.9%和0.3%,错误增加的城市元胞分别为21.8%和17.7%,表明SARCA在避免替代性错误方面好于LogCA。两种模型的数量错误小于位置错误,表明CA模型的模拟错误在2015年同样主要来自位置差异;和LogCA模型比较,SARCA模型数量和位置错误均较小,表明SARCA预测效果更好。

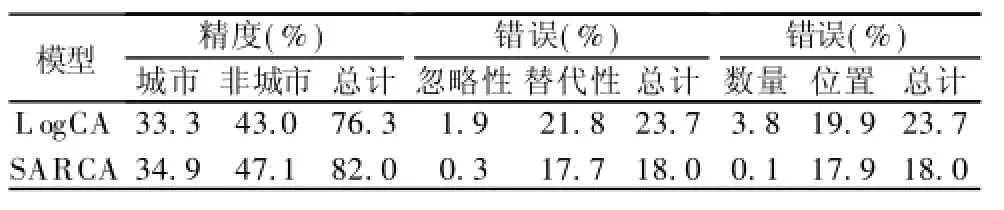
表5 2015年两种模型的预测精度Table 5 Prediction accuracies of the two CA models in 2015

3 结论

本文考虑空间自相关,构建了一种基于空间自回归(SAR)的地理CA模型——SARCA模型,该方法在CA建模中有效考虑了空间自相关,因此其模型拟合残差为随机分布或仅具有很弱的空间自相关特征。上海市全域土地利用变化模拟(1995-2015年)表明,SAR在AIC、残差的描述性统计量和空间自相关指标等方面均优于Logistic回归。CA参数和城市土地转化概率表明,上海市外环线对于CA参数的贡献相比其他空间变量具有压倒性优势,即上海城市边缘区在外环线附近,到外环线距离越近则土地发展为城市的概率就越大。该SARCA模型适用于快速城市化区域,能够较好地捕捉城市发展的主要驱动因素并确定其贡献。

上海市2005年土地利用模拟表明,LogCA模型的总体精度为79.8%,SARCA模型的总体精度提高了6.5%,为86.3%;对于2015年,LogCA模型的总体精度为76.3%,SARCA模型的总体精度提高了5.7%,为82.0%;两种CA模型的模拟精度随时间均有所下降,但是SARCA的模拟效果显然优于LogCA模型。2005-2015年的模拟仅用了1995 -2005年数据校正的模型,但后10年随着上海城市的发展导致空间变量与前10年相比发生了较大的改变,因此较旧的空间变量致使预测精度降低。这表明如果要获得更加准确的模拟预测结果,需要对空间变量、模型参数进行必要的校正。未来研究中将利用长三角中等城市作为案例,考虑不同地形、影响和限制因素的影响,验证该SARCA模型在不同条件下的适用性与模拟效果。此外,SAR模型本质上是一种线性模型,在表达城市发展的复杂边缘方面有其局限性;本文中SARCA的建模没有考虑空间变量多重共线的影响,未来研究中将首先确定空间变量的最佳组合,在消除共线关系的基础上构建新的SARCA模型,可望能够获取更为有效的CA模型和更好的模拟结果。

[1] TOBLER W R.A computer movie simulating population g rowth in the Detroit region[J].Economic Geography,1970,42:234-240.

[2] 周成虎,孙战利,谢一春.地理元胞自动机研究[M].北京:科学出版社,1999.

[3] 黎夏,叶嘉安,刘小平,等.地理模拟系统——元胞自动机与多智能体[M].北京:科学出版社,2007.

[4] LIU X P,OU J,LI X,et al.Combining system dynamics and hybrid particle swarm optimization for land use allocation[J].Ecological Modelling,2013,257:11-24.

[5] 杨青生,黎夏.基于动态约束的元胞自动机与复杂城市系统的模拟[J].地理与地理信息科学,2006,22(5):10-15.

[6] LIU X P,LI X,LIU L,et al.A bottom-up approach to discover transition rules of cellular automata using ant intelligence[J]. International Journal of Geographical Information Science, 2008,22(11-12):1247-1269.

[7] 冯永玖,童小华,刘妙龙,等.基于GIS的地理元胞自动机模拟框架及其应用[J].地理与地理信息科学,2010,26(1):41-43.

[8] 马世发,艾彬,念沛豪.基于约束性CA的土地利用规划预评估及警情探测[J].地理与地理信息科学,2014,30(4):51-55.

[9] CAO M,BENNETT S J,SHEN Q,et al.A bat-inspired approach to define transition rules for a cellular automaton model used to simulate urban ex pansion[J].International Journal of Geographical Information Science,2016,30:1-19.

[10] LIAO J F,TA NG L N,SHAO G F,et al.A neighbor decay cellular automata approach for simulating urban ex pansion based on particle swarm intelligence[J].International Journal of Geographical Information Science,2014,28(4):720-738.

[11] 陶嘉,黎夏,刘小平,等.分析学习智能元胞自动机及优化的城市模拟[J].地理与地理信息科学,2007,23(5):43-47.

[12] 黎夏,李丹,刘小平,等.地理模拟优化系统GeoSOS及前沿研究[J].地球科学进展,2009,24(8):899-907.

[13] WU F.Calibration of stochastic cellular automata:T he application to rural-urban land conversions[J].International Journal of Geographical Information Science,2002,16(8):795-818.

[14] LI X,YEH A G-O.Neural-network-based cellular automata for simulating multiple land use changes using GIS[J].International Journal of Geographical Information Science,2002,16 (4):323-343.

[15] LI X,YEH A G-O.U rban simulation using principal components analysis and cellular automata for land-use planning[J]. Photogrammetric Engineering and Remote Sensing,2002,68 (4):341-351.

[16] 冯永玖,童小华,刘妙龙.基于偏最小二乘地理元胞模型的城市生长模拟[J].同济大学学报(自然科学版),2010,38(4): 608-612.

[17] 冯永玖,刘妙龙,童小华,等.基于核主成分元胞模型的城市演化重建与预测[J].地理学报,2010,65(6):665-675.

[18] LIU X P,LI X,SHI X,et al.Simulating complex urban development using kernel-based non-linear cellular automata[J]. Ecological Modelling,2008,211(1-2):169-181.

[19] 杨青生,黎夏.基于粗集的知识发现与地理模拟——以深圳市土地利用变化为例[J].地理学报,2006,61(8):882-894.

[20] LIU Y.M odelling sustainable urban growth in a rapidly urbanising region using a fuzzy-constrained cellular automata approach[J].International Journal of Geographical Information Science,2012,26(1):151-167.

[21] 黎夏,刘小平.基于案例推理的元胞自动机及大区域城市演变模拟[J].地理学报,2007,62(10):1097-1109.

[22] LI X,YANG Q,LIU X.Discovering and evaluating urban signatures for simulating compact development using cellular automata[J].Landscape and U rban Planning,2008,86(2):177 -186.

[23] 冯永玖,童小华,刘妙龙.城市形态演化的粒子群智能随机元胞模型与应用——以上海市嘉定区为例[J].地球信息科学学报,2010,12(1):17-25.

[24] FENG Y,LIU Y.A heuristic cellular automata approach for modelling urban land-use change based on simulated annealing [J].International Journal of Geographical Information Science,2013,27(3):449-466.

[25] L IU X P,LI X,SHI X,et al.A multi-type ant colony optimization(M ACO)method for optimal land use allocation in large areas[J].International Journal of Geographical Information Science,2012,26(7):1325-1343.

[26] LI X,LAO C H,LIU X P,et al.Coupling urban cellular automata with ant colony optimization for zoning protected natural areas under a changing landscape[J].International Journal of Geographical Information Science,2011,25(4):575-593.

[27] 刘小平,黎夏,张啸虎,等.人工免疫系统与嵌入规划目标的城市模拟及应用[J].地理学报,2008,63(8):882-894.

[28] LIU X P,LI X,SHI X,et al.Simulating land-use dynamics under planning policies by integrating artificial immune sy stems with cellular automata[J].International Journal of Geog raphical Information Science,2010,24(5):783-802.

[29] 杨青生,黎夏.基于支持向量机的元胞自动机及土地利用变化模拟[J].遥感学报,2006,10(6):836-846.

[30] FENG Y,LIU Y,BAT TY M.Modeling urban growth with GIS based cellular automata and least squares SVM rules:A case study in Qingpu-Songjiang area of Shanghai,China[J]. Stochastic Environmental Research and Risk Assessment, 2016,30(5):1387-1400.

[31] 何春阳,史培军,陈晋,等.基于系统动力学模型和元胞自动机模型的土地利用情景模型研究[J].中国科学(D辑),2005,35 (5):464-473.

[32] ARSANJANI J J,HELBICH M,KAINZ W,et al.Integrationof logistic regression,Markov chain and cellular automata models to simulate urban expansion[J].International Journal of Applied Earth Observation and Geoinformation,2013,21: 265-275.

[33] CLIFF A D,ORD J K.Spatial Processes:M odels&Applications[M].Pion London,1981.

[34] OVERMARS K,DE KONING G,VELDKAM P A.Spatial autocorrelation in multi-scale land use models[J].Ecological modelling,2003,164(2):257-270.

[35] ANSELIN L.Estimation Methods for Spatial Autoregressive Structures:A Study in Spatial Econometrics[M].Program in Urban and Regional Studies,Cornell University,1980.

[36] LIU Y L,HE Q,TAN R,et al.Modeling different urban growth patterns based on the evolution of urban form:A case study from Huangpi,Central China[J].Applied Geography,2016, 66:109-118.

[37] 冯永玖,刘妙龙,韩震.集成遥感和GIS的元胞自动机城市生长模拟——以上海市嘉定区为例[J].长江流域资源与环境, 2011(1):9-13.

[38] T EAM R C.R:A language and environment for statistical computing[A].R Foundation for Statistical Computing[C].Vienna,Austria,2013.2014,ISBN 3-900051-07-0.

[39] ANSELIN L,SYABRI I,KHO Y.GeoDa:An introduction to spatial data analysis[J].Geographical Analysis,2006,38(1):5-22.

[40] 冯永玖,刘艳,韩震.不同样本方案下遗传元胞自动机的土地利用模拟及景观评价[J].应用生态学报,2011,22(4):957-963.

[41] 廖江福,唐立娜,王翠平,等.城市元胞自动机扩展邻域效应的测量与校准研究[J].地理科学进展,2014,33(12):1624-1633.

[42] PONTIUS R G,MILLONES M.Death to Kappa:Birth of quantity disagreement and allocation disag reement for accuracy assessment[J].International Journal of Remote Sensing,2011, 32(15):4407-4429.

Simulation and Prediction of Urban Land Use Change with Spatial Autoregressive Model Based Cellular Automata

FENG Yong-jiu1,2,YANG Qian-qian1,CUI Li1,LIU Yan3
(1.College of Marine Sciences,Shanghai Ocean University,Shanghai201306,China;2.Key Laboratory of Sustainable Ex ploitationof Oceanic Fisheries Resources(Shanghai Ocean University),Ministry of Education,Shanghai201306,China; 3.School of Geography Planning and Environmental Management,University of Queensland,Brisbane QLD 4072,Australia)

This paper presents a spatial autoregressive(SAR)model based cellular automata model(SARCA)to simulate complex urban land use change by incorporating spatial autocorrelation.The CA parameters retrieved by the SAR model have clear physical meanings closely associated with urban land use.The proposed CA model has been used to simulate urban land use change of Shanghai from 1995 to 2015.CA parameters and land conversion probability maps show that the outer ring expressway of Shanghai has the most contribution to CA transition rules.T his indicates that the closer a land parcel to the outer ring expressway the higher its probability being converted from non-urban to urban.T he Logistic regression based CA(LogCA) model as a comparative model has also been implemented to the same study area.The fitting performance of CA transition rules shows that SAR is better than logistic regression as reflected by the Akaike Information Criterion(AIC)and the statistics and Moran′s I for residuals.T he simulation results demonstrate that the overall accuracy of SARCA is 86.3%in 2005 and 82.0%in 2015,indicating that the proposed CA model has a better performance in simulating urban land use change than the LogCA model(79.8%in 2005 and 76.3%in 2015).

cellular automata;urban land use change;spatial autoregressive(SAR)model;Logistic regression;Shanghai

F301.24

A

1672-0504(2016)05-0037-08

10.3969/j.issn.1672-0504.2016.05.006

2016-07-15;

2016-08-24

国家自然科学基金(41406146);上海市自然科学基金面上项目(13ZR1419300);教育部高等学校博士学科点专项科研基金新教师类项目(20123104120002)

冯永玖(1981-),男,博士,副教授,主要从事遥感与GIS应用、海岸带资源环境信息研究。E-mail:yjfeng@shou.edu.cn