含非线性部件的船舶推进轴系自由振动解析

肖能齐，周瑞平，林晞晨(武汉理工大学能源与动力工程学院，武汉430063)



含非线性部件的船舶推进轴系自由振动解析

肖能齐，周瑞平，林晞晨
(武汉理工大学能源与动力工程学院，武汉430063)

摘要：通过分析含非线性元件的扭转振动数学模型特点，建立单一质量点的非线性扭转振动方程，从而推导得到多自由度系统非线性扭转振动通用方程。研究谐波平衡法以及摄动法在求解非线性系统的优缺点，提出采用摄动-谐波法求解多自由度系统非线性振动方程，推导得到自由振动通用计算公式，为求解非线性多自由度系统自由振动提供了一定的理论指导和参考。

关键词：振动与波；非线性；扭振；推进轴系；自由振动

随着造船技术的发展，船舶动力装置向着大型化、复杂化和自动化发展，其推进轴系中会出现多个高弹性联轴器等非线性部件，使得该系统具有非线性扭转振动特性。与轴系线性振动问题求解相比较，含非线性元件的轴系扭转振动问题在理论和方法上有很大的差异。

非线性振动问题在工程上广泛存在[1–3]，国内外许多学者对求解非线性振动问题进行了研究。如文献[4]采用多尺度法对刚度分段线性系统的非线性振动方程进行求解，得到分段线性保守自治系统自由振动解析解的通用公式。文献[5]提出在单自由度强非线性振动方程中，引入人工参数以及采用Lindstedt-Poincare方法，求解非线性自由振动。文献[6]采用非线性振动平均法求解具有非线性特性的三圆盘扭转振动模型在系统满足3:1型内共振的解。

以含非线性元件的扭转振动数学模型为研究对象，分析线性部分、非线性部分和既含线性部分也含非线性部分三种基本模型的特点，建立某质量点的扭转振动基本方程，从而得到含非线性元件的多自由度系统扭转振动方程；同时通过对多自由度系统扭转振动方程的分析，采用摄动-谐波平衡法推导得到自由振动通用计算公式。

1　数学模型与一般方程

由船舶推进轴系扭转振动当量系统集总参数理想模型的简化原则可知，在推进轴系系统中，大部分元件的惯量、刚度和阻尼特性均可以以线性来简化或者近似线性特性来简化。由于高弹性联轴器依靠橡胶等实现扭矩的传递，因此在船舶推进轴系系统实际工程中其刚度和阻尼非线性总是存在，且刚度具有三次非线性特性[7]。

不论是对于传统的船舶推进轴系还是当前广泛运用的复杂混合动力推进轴系，按照扭转振动当量系统简化原则，均可以简化成类似于如图1所示的推进轴系集总参数扭转振动模型，其扭转振动模型由线性部分和非线性部分组成。下面将讨论线性部分、非线性部分和既含线性部分也含非线性部分三种基本模型，建立质量点扭转振动一般方程。

图1　推进轴系集总参数扭转振动模型

如图2所示模型只含线性部分时，第k质量点的扭转振动一般方程为

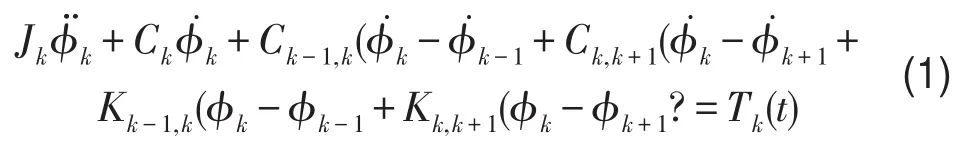
式（1）可转化为

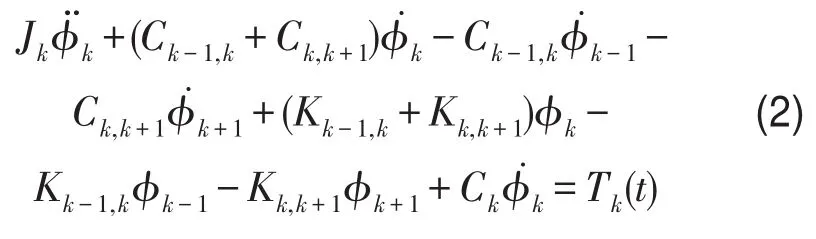
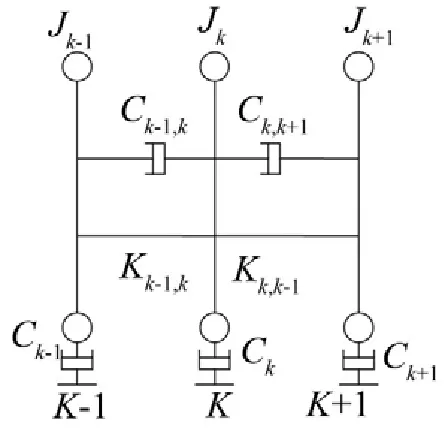
图2　模型只含线性部分

如图3所示，模型只含非线性部分时，即刚度具有三次非线性特性时有

其中常数K10、K11、K12、K20、K21、K22均与材料特性有关；Uk-1,k和Uk,k+1表示弹性力矩；。

由式(3)—式(4)，第k质量点的非线性扭转振动一般方程为

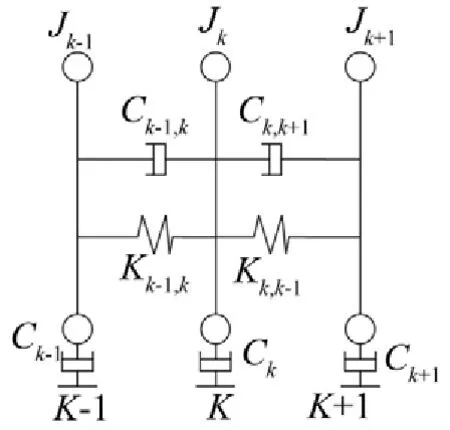
图3　模型只含非线性部分

如图4所示，模型含线性和非线性部分时，同理可知第k质量点的扭转振动一般方程为

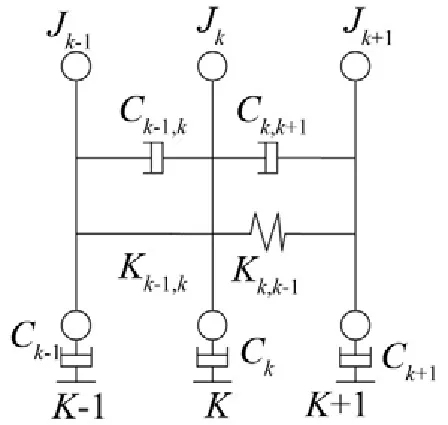
图4　模型含线性和非线性部分

2　摄动-谐波平衡法求解轴系自由振动

不考虑非线性元件的推进轴系理想扭转振动数学模型，根据式（1）可以得到扭转振动方程

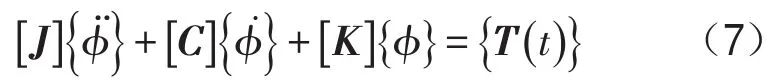
其中，转动惯量矩阵[J]为对角矩阵；刚度矩阵[K]为三对角矩阵；阻尼矩阵[C]为内阻尼（三对角矩阵）和外阻尼矩阵（对角矩阵）之和；{T(t)}为作用于系统的激励力矩向量。

而对于含非线性元件的推进轴系扭转振动模型，由式（1）、式（5）和式（6）可得到扭转振动方程

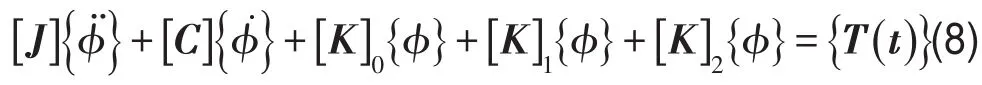
其中[J]、[C]和[K]0含义同上；而[K]1为{ϕ}的一次函数，[K]2为{ϕ}的二次函数。显然，对于线性部分{ϕ}的一次函数和二次函数系数为0。

对于非线性系统的求解，若采用传统的谐波平衡法，但其具有精度不高的不足，需对解的结果有一定的预判，在实际应用中较为困难；而传统摄动法需要进行大量繁琐的微分运算，随着摄动方程阶数的提高而求解难度增加。因此提出在谐波平衡法的基础之上引入摄动思想，实现二种方法的优势互补。由于篇幅原因，仅讨论含非线性元件的推进轴系扭转振动模型的非线性无阻尼自由振动求解问题，即

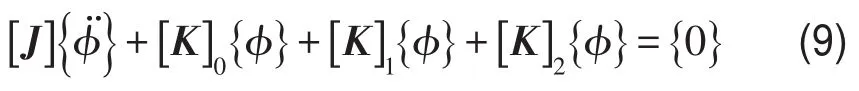
假定式（9）解的形式为

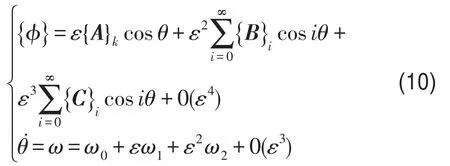
将式（10）代入式（9）各项，可知

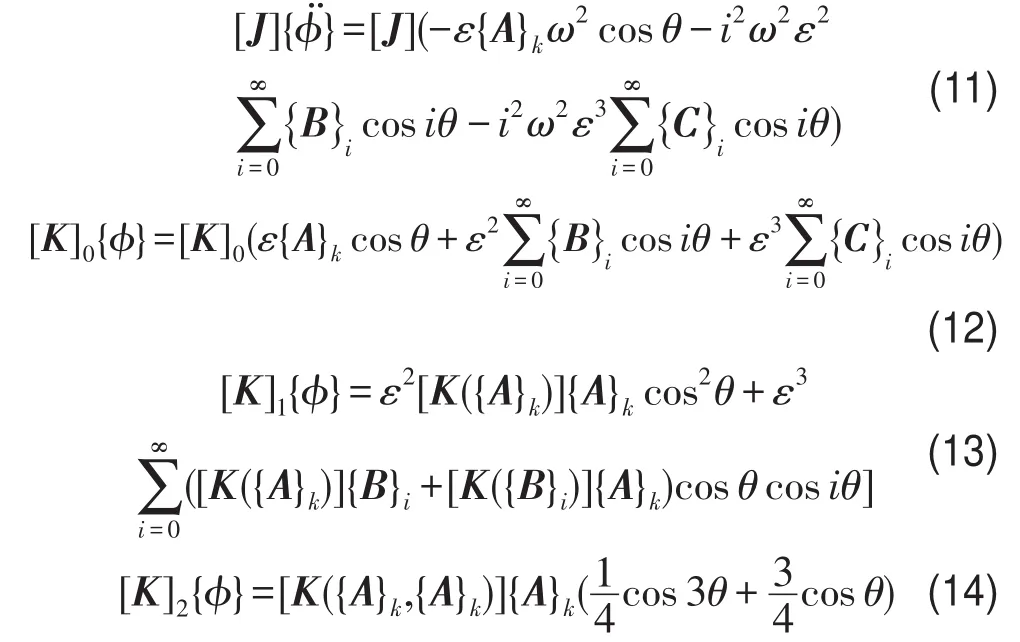
将式(11)—式(14)左右两边相加，变形后可得

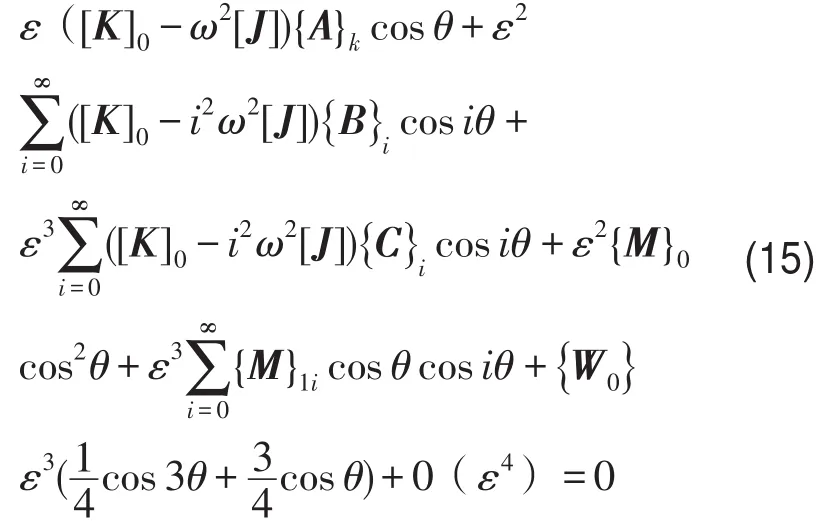
通过比较cosθ、cosiθ等各项前的系数可以得到：

1）常数项

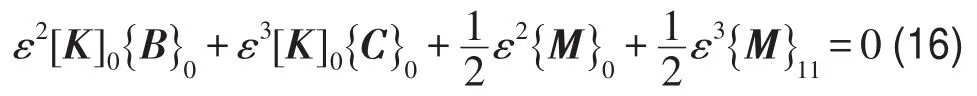
2）当i=1时cosθ前系数

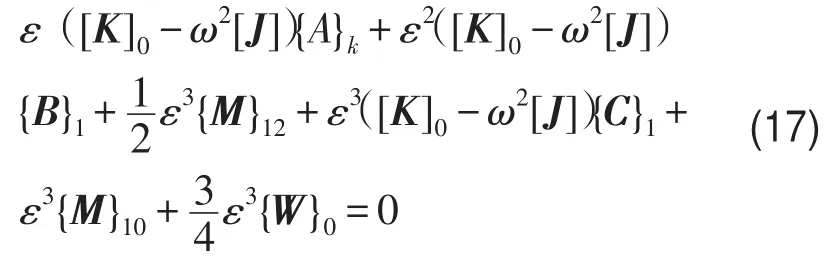
3）当i=2时cos2θ前系数

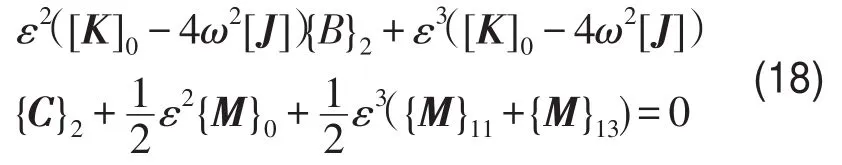
4）当i=3时cos3θ前系数

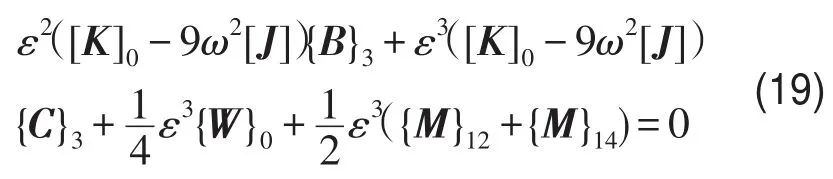
5）当i＞3时cosiθ前系数

λ值使得

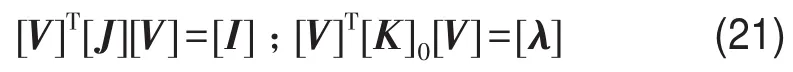
其中[I]为单位矩阵。

为将式(16)至式(20)进行线性等价变换，设

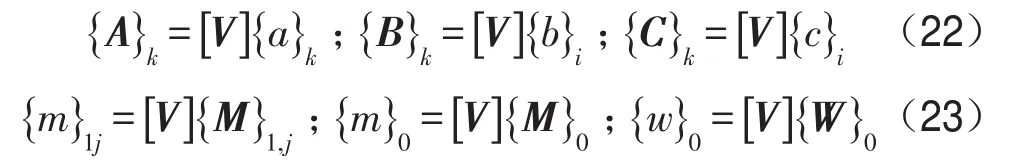
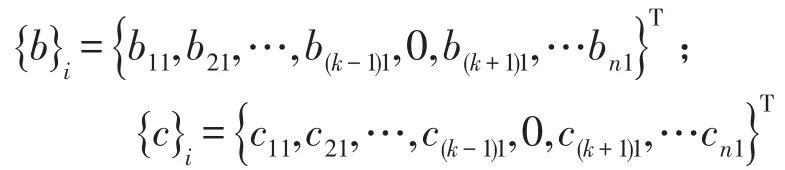
将式(22)、式(23)代入式(16)至式(20)，变形后可得

(1)常数项

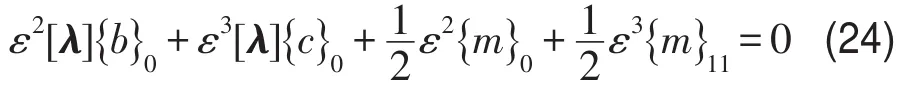
(2)当i=1时cosθ前系数

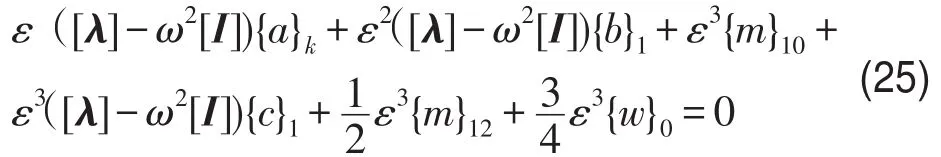
(3)当i=2时cos2θ前系数

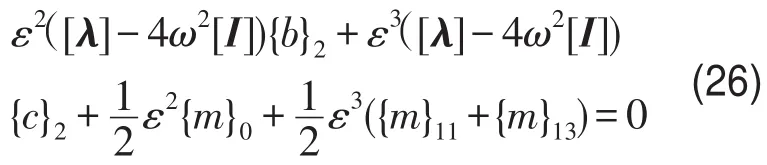
(4)当i=3时cos2θ前系数

(5)当i＞3时cosiθ前系数

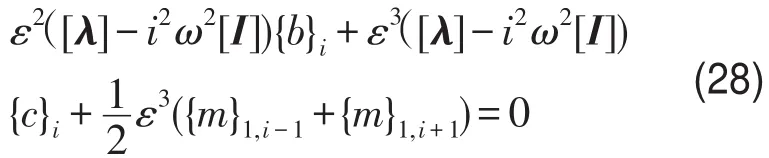
根据式(25)至式(28)和式(9)可知

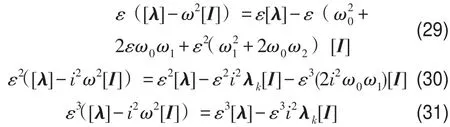
按照同次幂系数关系对上述方程进行求解，根据式(24)求解得

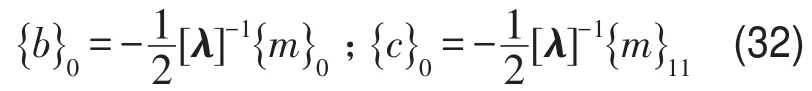
根据式(25)、式(29)和式(30)联合求解得

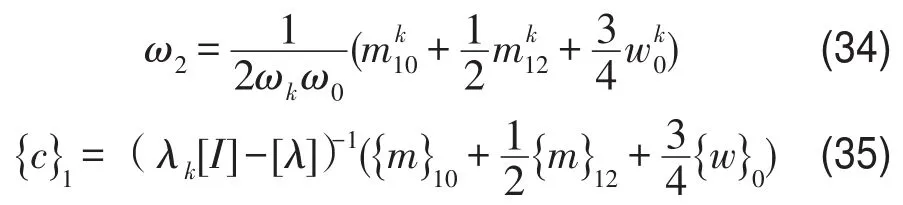
根据式(26)求解得

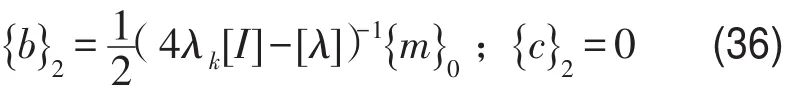
根据式(27)求解得

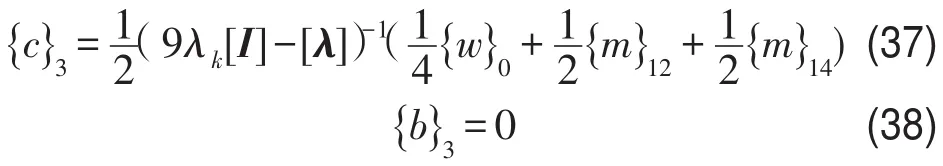
根据式(28)求解得

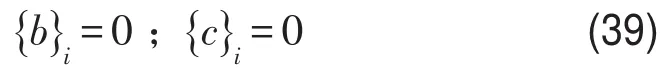
综上所述，可以得到

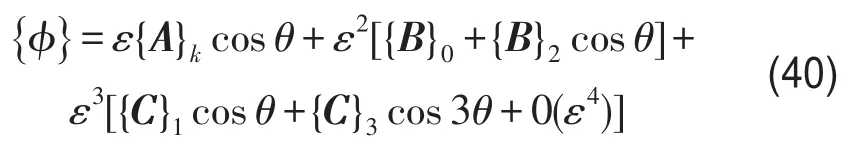
3　实例计算与分析

某船舶推进轴系系统按照当量系统集总参数理想模型的简化原则，推进轴系扭转振动当量参数如表1所示。当量系统图如5所示，其中高弹性联轴器刚度具有三次非线性特性，即弹性力为

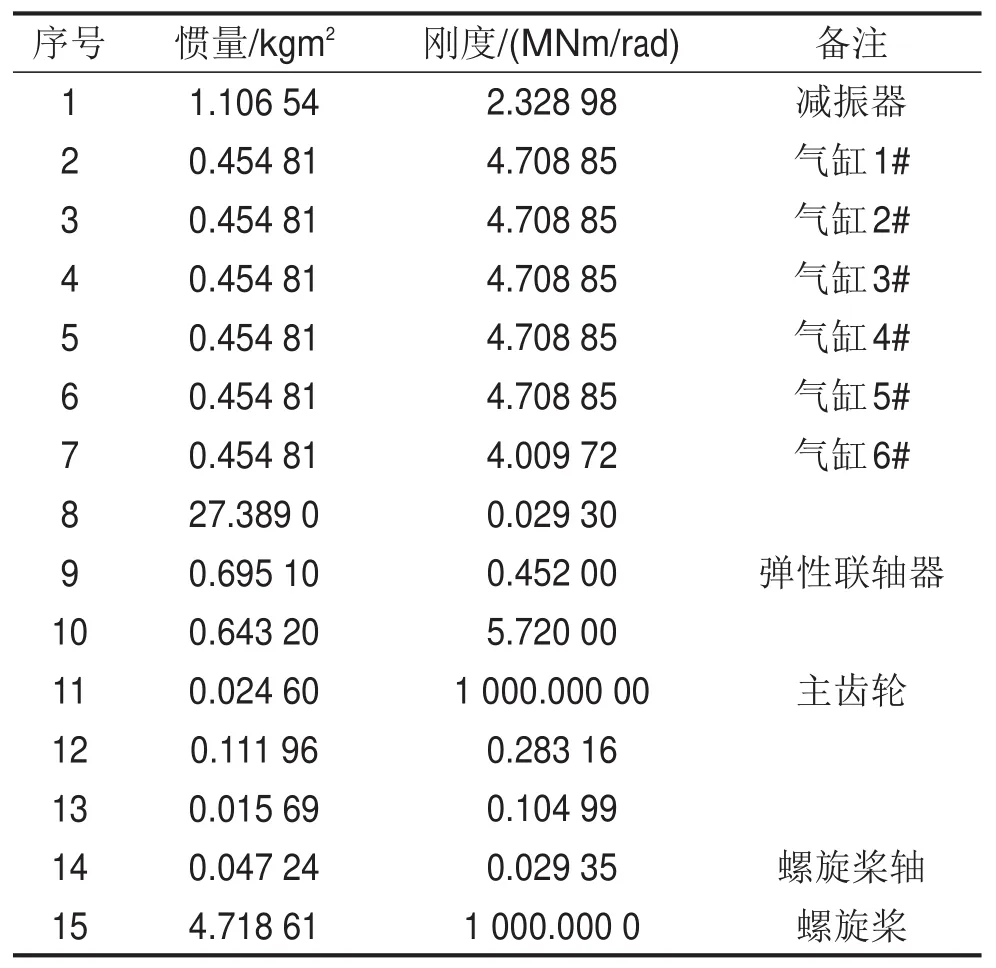
表1　某船舶推进轴系扭转振动当量参数

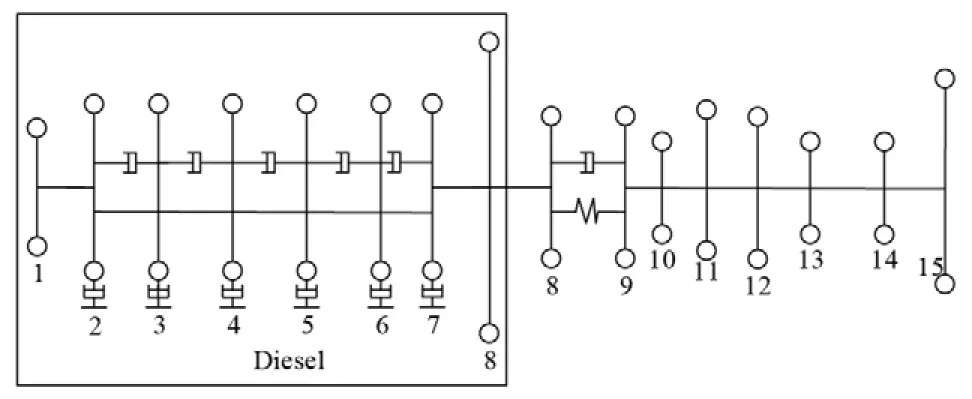
图5　某船舶轴系扭转振动当量系统图

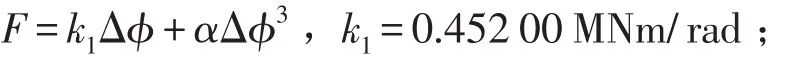
α=0.7 MNm/rad3。

利用摄动-谐波平衡法求解，对船舶推进轴系系统进行自由振动计算，计算结果如表2所示。表中给出了系统一阶固有频率的计算结果，其中振幅为系统第9质量点处振幅。对于系统其他阶固有频率同理也可以求出。

表2　1阶固有频率值

为了验证摄动-谐波平衡法得到的非线性扭转振动自由振动通用计算公式的正确性，采用ANSYS软件用有限元法进行验证。其中转动惯量通过MASS21质量单元表述，扭转刚度通过弹簧单元COMBIN14表述，可以得到如图6所示的某船舶轴系扭转振动有限元模型。

图6　某船舶轴系扭转振动有限元模型图

利用弹性联轴器具有非线性刚度的特点和表格2所示的振幅计算得到弹性联轴器的刚度，将刚度值依次代入到ANSYS软件所建立的振动模型中进行模态分析，从而验证了摄动-谐波平衡法得到的非线性扭转振动自由振动通用计算公式的正确性。由于篇幅有限，仅给出振幅为0.2 rad时,系统一阶固有频率有限元模态分析结果，其大小为8.477 Hz，与理论计算结果基本一致，如图7所示。

若不考虑弹性联轴器的非线性特性，按照线性特性求解上述船舶推进轴系系统，其一阶转速为53.084 rad/s，即固有频率为8.448 Hz，且与振幅的大小没有任何关系。根据表2以及摄动-谐波平衡法求解轴系系统自由振动的计算公式可知，含非线性部

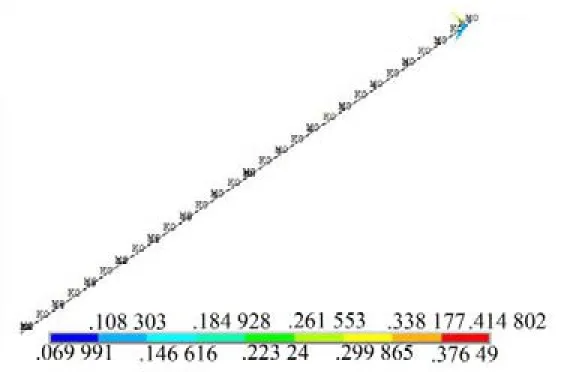
图7　振幅为0.2rad时系统1阶固有频率

件的轴系系统固有频率值随振幅的变化而变化，并非如同线性系统固有频率一样为固定值，因此按照部件实际的非线性特性计算，可以得到更为准确的系统固有频率，避免系统共振点的遗漏；同时可为后续研究含非线性部件的轴系系统强迫振动计算提供指导。

4　结语

(1)通过对含有非线性元件数学模型特点的分析，得到非线性扭转振动的一般方程，具有一定的通用性。

(2)结合谐波平衡法和摄动法的优缺点，提出运用摄动-谐波平衡法求解非线性扭转振动方程，从而得到非线性元件自由振动通用计算公式；使得轴系非线性振动问题求解过程变得简单。

(3)求解含非线性元件船舶推进轴系扭转振动固有频率，为后续研究含非线性元件轴系强迫振动提供了一定的理论指导和参考。

参考文献：

[1]韩放，郭杏林，高海洋.非线性油膜力作用下叶片-转子-轴承系统弯扭耦合振动特性研究[J].工程力学，2012，30 (4)：355-359.

[2]时培明，夏克伟，刘彬，等.含间隙多自由度轧机传动系统非线性扭振动力特性研究[J].机械工程学报，2012，48 (17)：57-64.

[3] Eddanguir A, Beidouri Z, Benamar R. Geometrically nonlinear transverse steady-state periodic forced vibration of multi- degree- of- freedom discrete systems with a distributed nonlinearity[J]. Ain Shams Engineering Journal, 2012, 3(3):191-207.

[4]闫政涛，翁雪涛，朱石坚，等.刚度分段线性系统的自由振动解析研究[J].噪声与振动控制，2010，30(6)：18-22.

[5]谢元喜，唐驾时.用人工参数法求解一类强非线性自由振动问题[J].振动与冲击，2005，24(4)：106-106.

[6]杨志安，李文兰.三圆盘非线性扭转自由振动系统3:1型内共振[J].唐山学院学报，2003，(4)：66-68.

[7]李芳，蔡耀全，朱来刚.冲击载荷下弹性联轴器刚度非线性特性影响[J].舰船电子工程，2014，(11)：143-145.

Analysis of Free Vibration of Marine Propulsion Shafting System with Nonlinear Components

XIAO Neng-qi , ZHOU Rui-ping , LIN Xi-chen
( School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China)

Abstract:Through the analysis of the characteristics of torsional vibration of the marine propulsion shafting system with nonlinear components, a single- mass nonlinear torsional vibration equation was established, and then the general equations for multi- DOF nonlinear torsional vibration of the system were derived. Harmonic balance method and perturbation method were used to solve these equations, and the advantage and disadvantage of these methods were analyzed. The general free- vibration formulas were formulated. This work may provide a theoretical guidance and a referencefor multi-DOFnonlinear freevibrationanalysis.

Key words:vibrationandwave; nonlinear; torsional vibration; propulsionshafting; freevibration

通讯作者：周瑞平(1964- )，男，教授，博士生导师。E-mail:rpzhouwhut@126.com

作者简介：肖能齐（1987-）男，湖北省汉川市人，博士生，主要研究方向为船舶动力装置性能分析与减振降噪。E-mail:xiaonengqi@126.com

基金项目：科技部2013年专项船舶柴电混合电力系统关键技术开发资助项目（2014BAG04B02）

收稿日期：2015-10-12

文章编号：1006-1355(2016)02-0135-04+214

中图分类号：U664.21

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.030