非平面运动球式自动平衡装置稳定性分析

罗　建，谭　青，江　波（中南大学机电工程学院，长沙410083）



非平面运动球式自动平衡装置稳定性分析

罗建，谭青，江波
（中南大学机电工程学院，长沙410083）

摘要：在实际生产工作中，高速运动转子由于受到不平衡力矩作用，会使整个转轴产生空间转动，这种转动使得转子产生非平面运动。采用拉格朗日方程和牛顿定律，建立一种非平面运动球式自动平衡装置数学模型；通过摄动法和劳斯-霍尔维茨判据对其可能使系统稳定的解进行分析，得出该自动平衡装置分别在1个球和2个球的情况下存在能够使系统稳定的解以及系统在不同条件下振动情况。该装置在过临界转速下存在稳定点，在一定条件下能对不平衡力进行平衡，达到减振目的。

关键词：振动与波；非平面运动；球式自动平衡装置；数学模型；稳定性分析；稳定解

对于高速回转机械而言，转子由于质量分布不均匀而产生不平衡力将导致回转机械产生振动和噪声，严重的甚至会引发灾难性破坏，由此造成的损失不容忽视。目前，为了解决这一问题一般对回转部分（即转子）采取高精度的动静平衡方法[1]。但对于一些质量分布可能发生变化的回转机械，经常将其卸载下来进行动静平衡不是很方便。由此，学术界对自动平衡课题展开了研究。自动平衡装置分为两种类型：一种是自动定心型的自动平衡装置，也称为被动式自动平衡装置[2]；另外一种是由微机控制的自动平衡装置，也成为主动式自动平衡装置[3，4]。

被动式自动平衡装置工作原理是：转子在过临界转速下旋转时，转子内可移动的质量将自动受到转子机械振动相位的影响，移动到偏心质量的另一边，从而在一定程度上抵消了由不平衡质量引起的离心惯性力，达到减振的效果[2]。主动式自动平衡装置的工作原理是：通过系统外部控制来改变对转子添加质量大小或位置的方法使系统质心与旋转轴心重合，以达到系统平衡效果。以往对被动式自动平衡转置的研究，主要集中在转盘平面不变的情况下进行，从而忽略了由不平衡力矩引起的非平面运动。另外，生产机械经常受到各种干扰，自动平衡状态如果不能稳定的话，就不能达到满意的减振效果。本文主要研究非平面运动球式自动平衡装置的建模问题，并对其中平衡状态的稳定性进行分析。

1　建立数学模型

非平面运动球式自动平衡装置的力学模型如图1所示。球式自动平衡装置安装在偏离转轴中心平面，这就使得整个系统产生了一个对转轴中心的不平衡力矩。系统在受到不平衡力矩作用时整个转轴产生一定的空间转动，从而使整个系统产生非平面运动。转盘上放置了n个滚球，作为可移动的补偿量，同时在转盘上安放了m个偏心质量。

现对本模型做如下假设：

（2）转盘为质量均匀分布的圆形薄盘，转轴质量分布均匀；

（3）将滚球和偏心质量当作质点；

（4）转盘与滚球之间的黏性阻尼力与速度成正比；

（5）不考虑轴向运动和重力作用；

（6）转轴是刚性的。

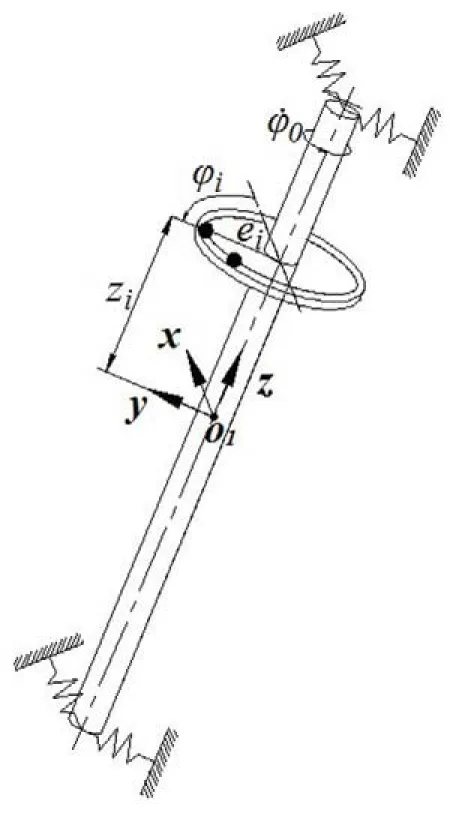
图1　非平面运动球式自动平衡装置力学模型

采用的符号如下：

(3)将第3行对角元以右的2个元素赋值给对角元以下的2个元素；再对第3行的2个元素规格化；继而对第3列元素消元，仅计算虚线框中的3个元素，见图5上图。

O0-XYZ：静止时的坐标系，O0为转轴中心静止时的位置；

O1-xyz：随转轴中心运动的坐标系，其中xy平面始终与转盘平面平行，O1是转轴中心运动时的位置；

x，y：转轴中心由O0到O1的位移，单位为m；

φx，φy：转轴空间转动的角位移，单位为rad；

zi为第i个质点与系统质心之间的轴向距离，单位为m；ei为第i个质点与回转轴线之间的距离即偏心距，单位为m；φi为第i个质点的转角，单位为rad（其中i =1，…，n，n+1，…，n+m，前n个质点为滚球，后m个质点为偏心质量）。

M为系统的总质量，m为转盘转轴的质量，mi为第i个质点的质量，单位为kg（其中M=m+）。

C、K分别为系统的阻尼矩阵、刚度矩阵，阻尼的单位为N·s/m，刚度的单位为N/m；

JRi、J分别为质点绕定轴转动的转动惯量矩阵、转轴与转盘的主转动惯量矩阵，转动惯量的单位为kg∙m2；

φ.0为转轴和转盘的转速，单位为rad/s；

C0为滚球黏性阻尼系数，单位为N∙s/(m∙rad)。

系统的数学模型可以通过以下方程进行描述

在式（1）中C、K分别表示阻尼矩阵和刚度矩阵[7]，为广义坐标矩阵，用它来描述系统的运动情况，Q为惯性力矩阵

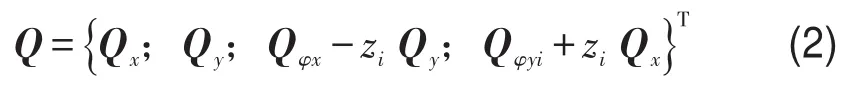
由第二类Lagrange方程[5]

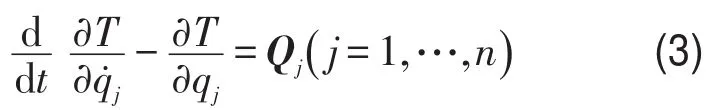
可以求得惯性力Q，其中T为动能。如图2所示，任意质点在XO0Y平面内的位移可以表示为

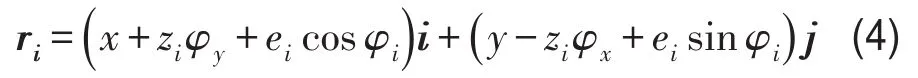
由式(3)可以得到此时每一个质点受到的惯性力

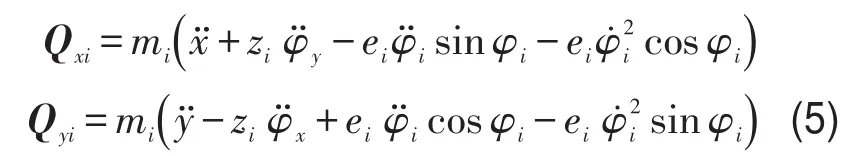
同理可以得到转盘和转轴受到的惯性力为

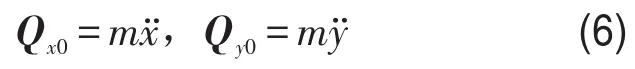
因此系统在这种运动情况下受到的惯性力为

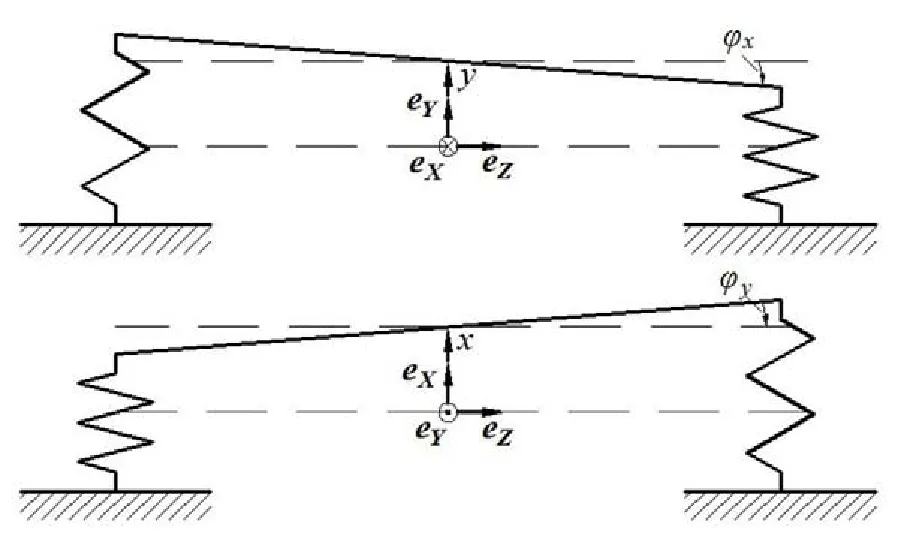
图2　模型在X O0Y平面的振动

系统的空间转动如图3所示，可以用卡尔丹角[6]进行描述。首先坐标系O1-XYZ绕轴X旋转角φx到达坐标系O1-x1y1z1，然后坐标系O1-x1y1z1绕轴y1旋转角φy到达坐标系O1-x2y2z2，最后坐标系O1-x2y2z2绕轴z2旋转角φi到达坐标系O1-xyz。由文献[7]、[8]可以得到滚球质点在空间转动时受到的惯性力

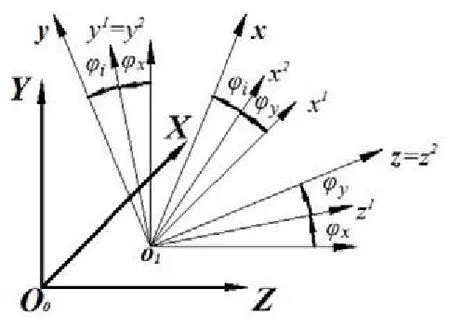
图3　模型空间转动

其中

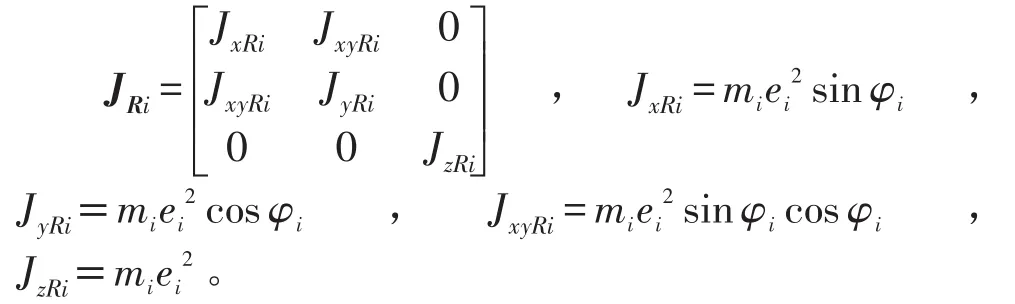
转轴与转盘的主转动惯量矩阵为

同理可以求得转轴和转盘在空间转动时的惯性力如式(11)

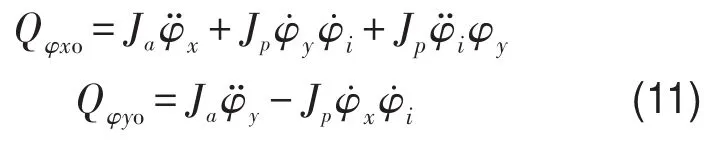
故系统的在空间转动运动时所受到的惯性力

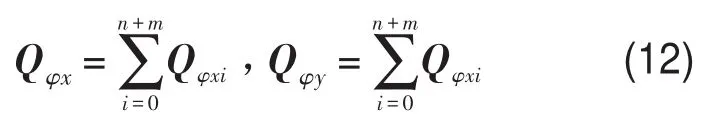
滚球在运动过程中受到一个惯性力和黏性阻尼力作用，其中黏性阻尼力

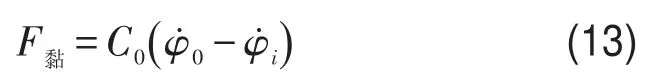
惯性力在黏性阻尼力方向上(圆盘切向方向)的分量

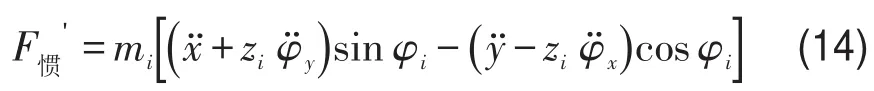
在圆盘切向方向上由牛顿定律可得

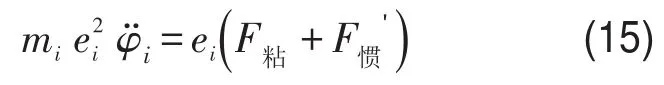
因为

故非平面运动球式自动平衡装置运动方程为

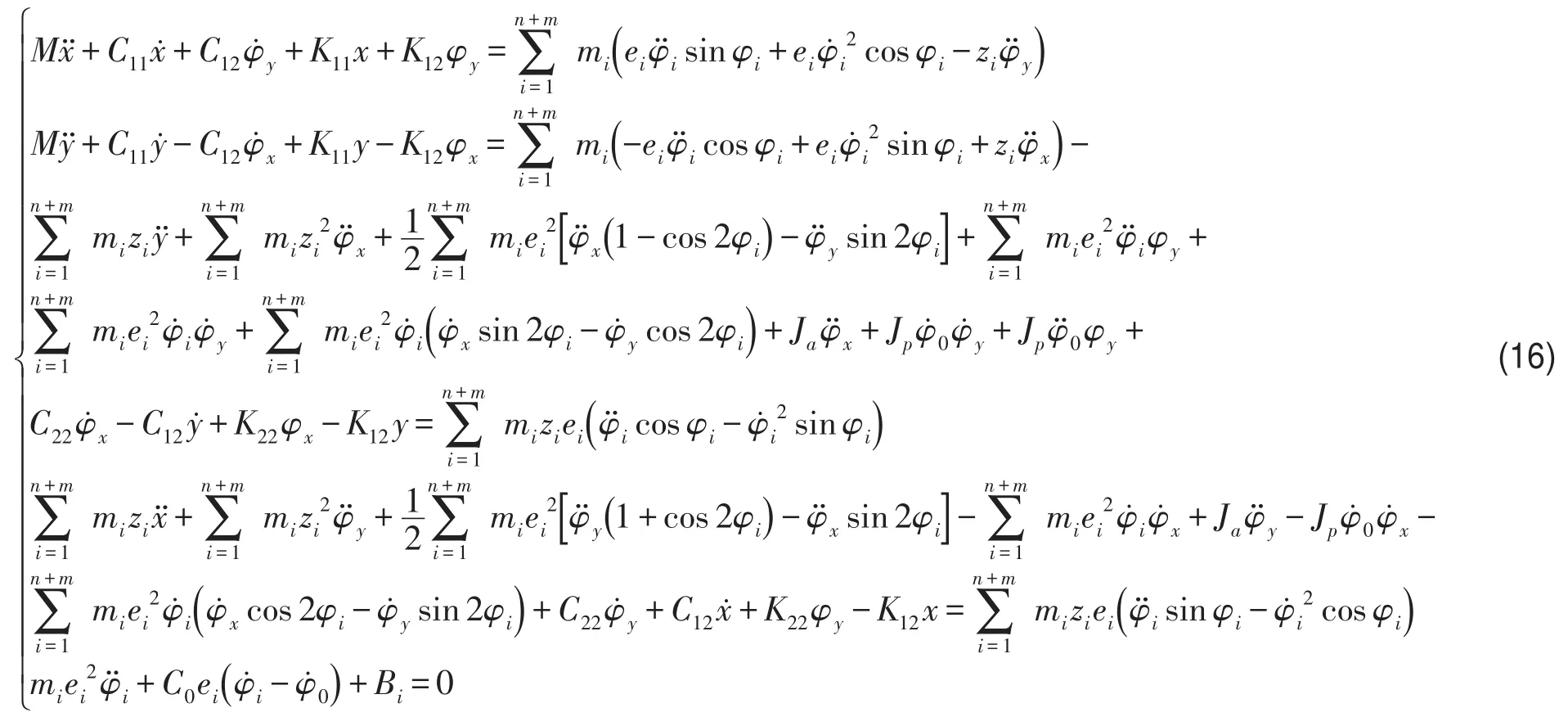
其中

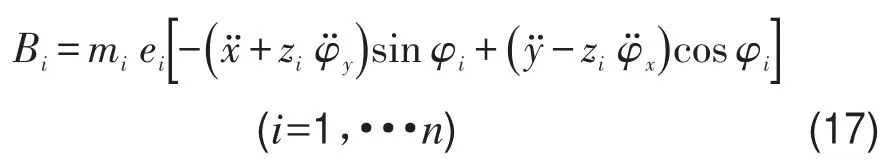
2　系统稳定性分析

在球式自动平衡装置中，滚球作为补偿量是可以自由移动的。在这样的系统中，滚球的运动是否稳定决定了系统是否稳定，故对系统的稳定性分析实质上是对滚球运动的稳定性进行分析。

系统在经过加速过程后达到过临界转速，由于电机驱动力足够大，系统将会以一个恒定转速运动，即转盘和转轴的角速度常量。当系统趋于稳定时，由自动定心理论可知滚球与偏心质量会保持一定相对角度，所以系统稳定时滚球的角速度近似于偏心质量的角速度，而偏心质量固定安放在转盘上，故，运用运动分离的方法[9]将滚球的角位移分为三个部分，即

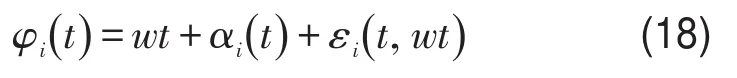
其中

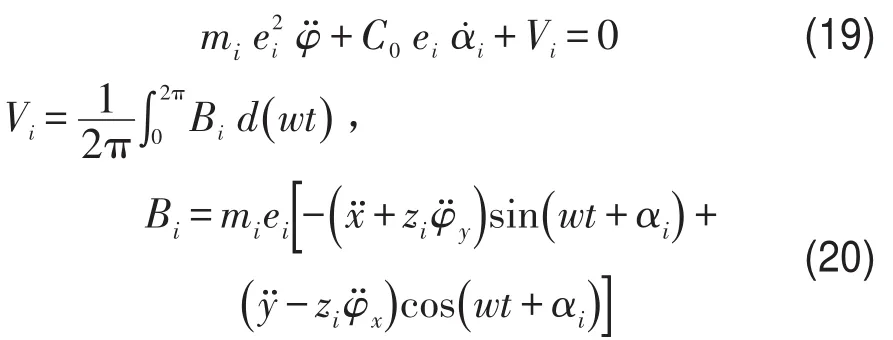
忽略系统中的阻尼，同时将一些在平衡时的小量忽略，将式(18)代入式(16)并且忽略式(18)中的项得到

将式(22)代入式(21)中并将其化为矩阵形式得到

解出r、φ的值，由此可以得到

其中

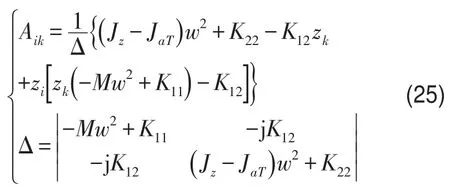
将式(24)代入式(20)得

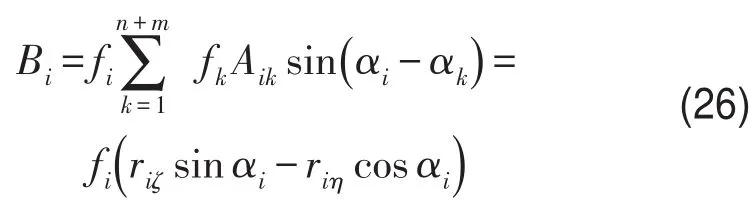
其中ζ，η是绕转盘一起转动的坐标轴

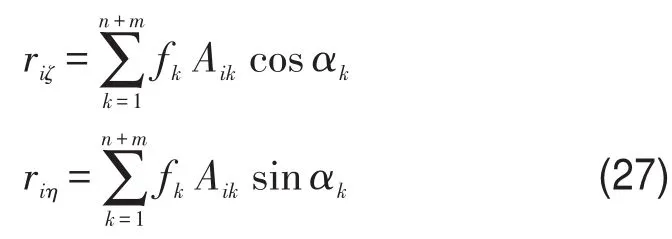
系统在稳定时，忽略式(18)中的快项，滚球会相对于转盘静止，即滚球会与转盘已设定好的初始位置形成一个恒定夹角αi=αi0=常量，要使系统稳定，结合式(19)和式(26)必定有

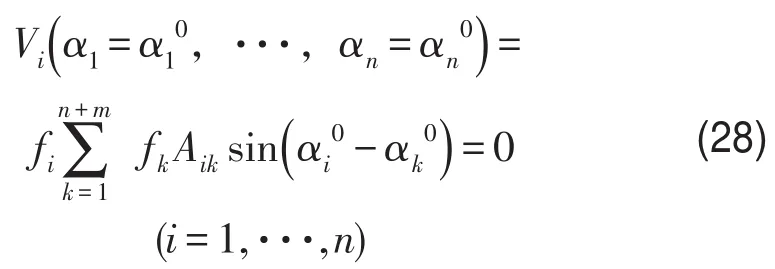
因为偏心质量固定安装在圆盘上，所以它们相对于已设定的初始位置的夹角是恒定不变的，即

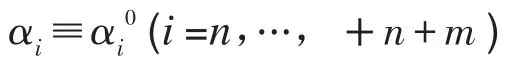
式(28)的解是可能使系统稳定的解，为了判断式(28)的解是否为使系统稳定的解，采用摄动法[10]，令，其中为小扰动量，可以得到

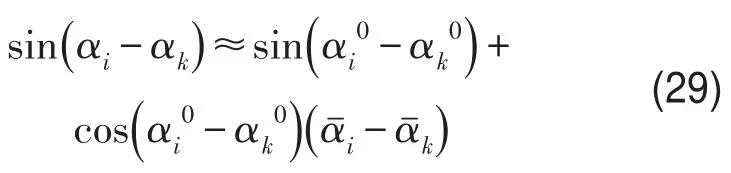
式(28)存在的一种解为

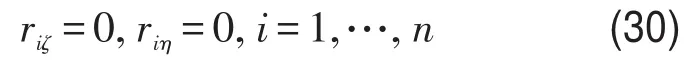
将式(28)、式(29)、式(30)代入式(19)，得

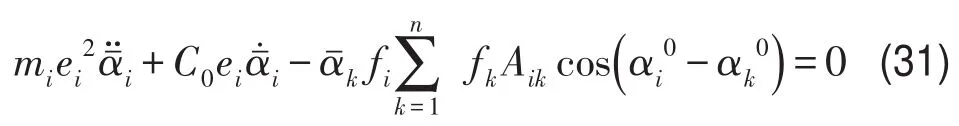
由劳斯-霍尔维茨判据[11]可知对于式(28)中的任意解，要使系统稳定，式(31)中的系数矩阵必需正定。文献[11]对多自由度系统的稳定性给出了判断依据。由于Co>0，故系统稳定的充要条件是的系数矩阵正定。

为了更直观地体现转盘所在平面在系统稳定时是否达到减振的目的，假设偏心质量的作用使转盘平面产生了振动位移，其作用方向与设定的转盘初始位置成角，其中

由式(27)、式(32)得

由式(28)、式(32)得

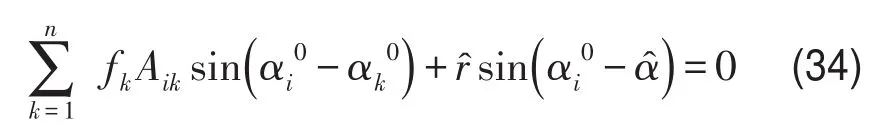
由式(19)、式(27)、式(28)、式(32)得

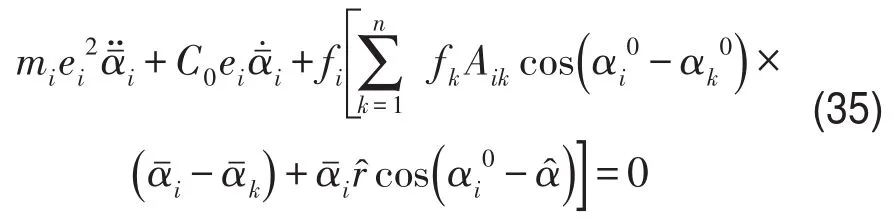
在这种情况下只需对式(35)的稳定性进行分析。

2.1系统存在一个球时的稳定性分析

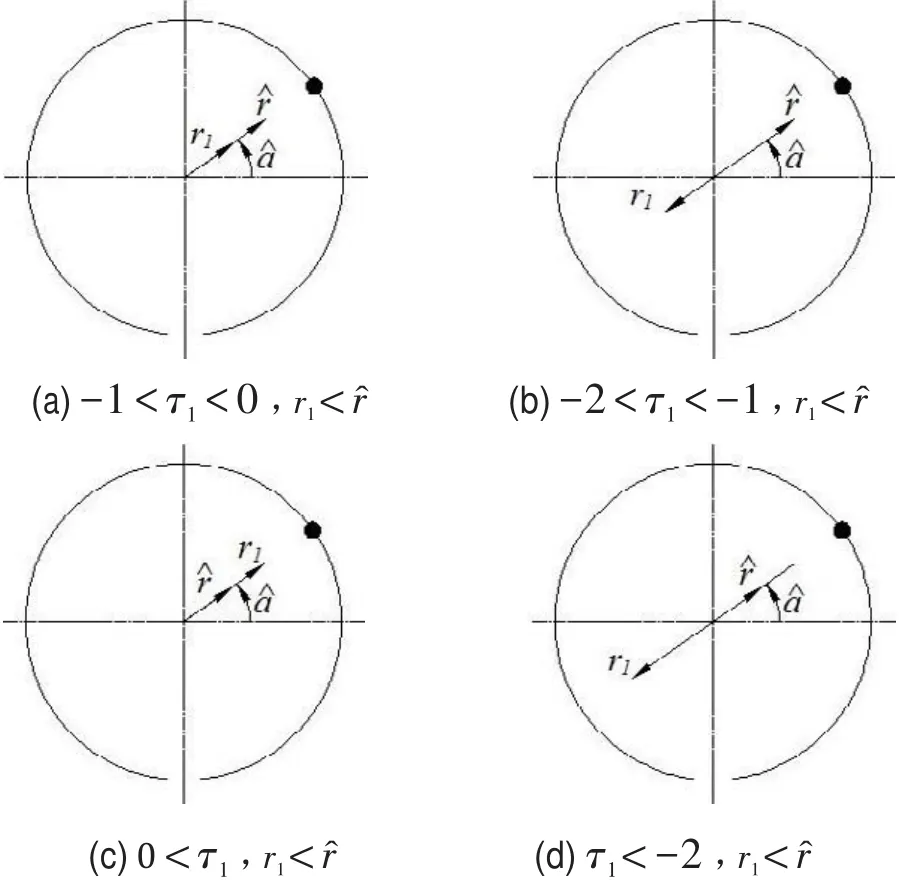
图4　在1个球的情况下系统稳定时球的位置

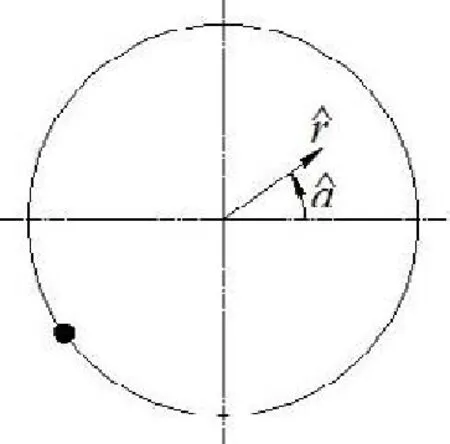
图5　在1个球的情况下系统不稳定时球的位置

2.2系统存在两个完全相同球时稳定性分析

由于是两个完全一样的滚球，又处在同一平面上，所以m1=m2，z1=z2，A11=A12=A21=A22，f1=f2。将已知条件代入式(30)、式(33)解得

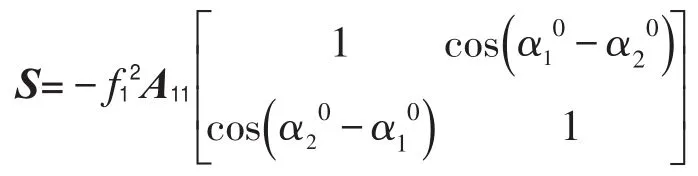
当A11<0时，S正定，即系统稳定。令，当τ2(w)≤-1且A11<0时，系统能够稳定并且达到完全减振，如图6(a)所示。

将已知条件代入式(34)中求解，得到3组解，将所得解代入式(35)得到的系数矩阵，通过判断系数矩阵S是否正定来确定该解是否为稳定解。

3　结语

非平面运动球式自动平衡装置存在稳定点，在过临界转速下整个系统能够稳定运行。在一定条件下整个系统不但能够稳定还能够达到减振的目的。在一个球的情况下，其存在一个稳定解，在一些条件下，自动平衡装置能够使系统减振；在两个相同球的情况下，其存在两个稳定解，在一些条件下，自动平装置能够使系统减振，甚至在某些特定条件下，自动平装置能够完全平衡偏心质量引起的离心力。

图6　在2个球情况下系统稳定时球的位置

图7　在2个球情况下系统不稳定时球的位置

参考文献：

[1]刘文倩，谭青，谢燕琴，等.自动平衡装置减振效益分析[J].噪声与振动控制，2010，30(4)：153-157.

[2]谭青，周铁，黄秀祥.球式自动衡装置的数值仿真与实验研究[J].噪声与振动控制，2008，28(3)：142-145.

[3]陶利民，葛哲学，温熙森.刚性转子自动平衡控制策略[J].机械科学与技术，2004，23(3)：142-145.

[4]曾胜，汪希萱.电磁式在线自动平衡调节器的原理及其实验[J].流体机械，1997，25(5)：11-14.

[5]黄昭度，纪辉玉.分析力学[M].北京：清华大学出版社，1985，51：61.

[6]刘延柱，洪嘉振，杨海兴.多刚体系统动力学[M].上海：高等教育出版社，1989，22：27.

[7] G Gent, C Delprete, E Busa. Some considerations on the basic assumptions in rotordynamics[J]. Journal of Sound and Vibration, 1999,227(3):611-645.

[8] Sperling L, Ryzhik B, Linz Ch. Simulation of two-plane automatic balancing of a rigid rotor. Mathematics and Computersin Simulation, 2002(58):351-365.

[9] Sperling L, Merten F, H Duckstein. Rotation und vibration in beispielen zur method der direkten bewegungsteilung [J]. Technische Mechanik, 1997,17(3):231-243.

[10] H H包戈留包夫，Ю A米特罗波尔斯基.非线性振动理论中的渐进方法[M].上海：上海科学技术出版社，1963：385-410.

[11]屈维德，唐恒龄.机械振动手册[M].北京：机械工业出版社，1992：547-550.

Stability Analysis of Ball-type Automatic Balancer Devices with Non-plane Motion

LUO Jian , TAN Qing , JIANG Bo
（School of Mechanical & Electrical Engineering, CSU, Changsha 410083, China）

Abstract:In the actual production, since imbalance moment is acting on the high-speed rotor, the whole shaft will produceaspatial motion, which can lead to non-planemotion of therotor. In thispaper, based on the Lagrangeequation and Newton’slaw, amathematical model of theball-typeautomatic balancer devicewith non-planemotion wasestablished. In order to obtain thepossiblestablesolution of themathematical model, perturbation method and Rolls-Hurwitz criterion were adopted to analyzethestability of thesystem. Through thisanalysis, it wasfound that thereexiststhestablesolution for the automatic balancer devicein thecasesof oneball or two balls.And thevibration of thesystem under different condition can be obtained. The device has stable solutions at over-critical speed, and it can also counterpoise the unbalanced force under certainconditionstoreducethevibration.

Key word:vibration and wave; non-plane motion; ball-type automatic balance device; mathematic model; stability analysis; stablesolution;

作者简介：罗建（1990-），男，硕士研究生，从事机械振动控制研究。E-mail:lj561791@163.com

收稿日期：2015-08-19

文章编号：1006-1355(2016)02-0021-06

中图分类号：TH113.1

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.005