具有非线性减振器的弹性双层隔振系统建模

韩修品，蒋丰（同济大学航空航天与力学学院，上海200092）



具有非线性减振器的弹性双层隔振系统建模

韩修品，蒋丰
（同济大学航空航天与力学学院，上海200092）

摘要：运用多体动力学理论、动态子结构方法，同时考虑中间质量弹性和隔振器刚度与阻尼非线性，建立一个弹性双层隔振系统动力学新模型。对所建模型进行编程计算，求出其在冲击激励下响应，并与有限元计算结果比较分析，验证所建力学模型正确性与合理性，在此基础上进一步分析中间质量弹性和非线性隔振器对双层隔振系统冲击响应影响。

关键词：振动与波；双层隔振系统；弹性板；非线性；冲击响应

舰船在冲击作用下，由于隔振器本身刚度和阻尼的非线性，隔振系统可具有明显非线性性质。李红钢和彭旭[1]进行了具有刚度非线性双层隔振系统冲击响应数值分析研究。商孝鹏[2]通过实验，对隔振器的非线性刚度和阻尼进行研究，总结隔振器在冲击作用下的特性，并建立舰船机电设备非线性抗冲击动力学方程。曹利[3]进一步使用具有非线性弹簧和非线性阻尼效应的隔振器，建立一个双层双非线性抗冲隔振系统的数学力学模型。但只是将中间质量假设为一个厚度可以忽略不计的刚体，而王志刚[4]建立了弹性浮筏线性隔振系统，研究表明中间质量的弹性引起的横向弯曲振动会对系统的动力学特性产生很大影响。

鉴于目前建立的双层隔振系统模型中鲜有同时涉及隔振器的刚度以及阻尼的非线性与中间质量弹性的研究，结合多体动力学理论[5]和动态子结构方法，建立一个同时考虑隔振器刚度、阻尼非线性，以及中间质量弹性的双层隔振系统的动力学模型。结合具体工程算例，分析隔振器非线性特性和中间质量弹性对隔振系统冲击响应的影响。

1　弹性双层隔振系统的动力学方程

1.1力学模型

双层隔振系统的力学模型如图1所示。过筏架的质心虚设一个刚性载体，记为B1；上层为机组设备，记为B2。隔振器安置方式为平置。

惯性坐标系的原点取在质量体的中垂线与地面的交点位置，x和y方向如图2所示，z方向为地面的中垂线方向，惯性基用表示。刚体Bm(m=1,2)的连体基，表示为；任一点i在惯性基下的坐标用ρcmi表示，对应其坐标方阵。姿态坐标用卡尔丹角θm表示，方向余弦阵。其中为θm的坐标方阵。记为

图1　双层隔振系统力学模型

沿B1的中面建立局部坐标系x-y，坐标原点取在矩形薄板中面的中点，其中( ) x,y为质量体B1中面上任一点坐标，w为水平薄板中面的挠度。

1.2隔振器弹性力、阻尼力及其力矩的确定

在建模时，将隔振器元件简化为非线性弹簧和非线性阻尼并联形式。下层隔振器ii'，总数为n1；上层隔振器jj'，总数为n2。

1.2.1隔振力数学模型

隔振器弹性力：主轴方向弹性力与位移的关系根据实验数据[6]用最小二乘法拟合，拟合公式（单位为N）为

将非线性弹性力和非线性阻尼力合并，形成了隔振器的非线性力，其数学模型为

1.2.2力矩的确定

（1）下层隔振器对B1质心的力矩B1Mc1i

（2）上层隔振器对B1质心的力矩和对B2质心的力矩

1.3系统刚体运动的自由振动方程

牛顿方程

欧拉方程

其中

1.4中间质量的弹性振动方程

弹性变形函数为

当矩形薄板的边界条件为四边自由时，板的振型函数可假设为[8]

其中a、b为B1的边长，并且参数ξ1满足条件：

中间质量的振动方程为

其中D为中间质量的抗弯刚度，E为杨氏弹性模量，μ为泊松比，h为厚度，ρ为密度，F为隔振力。式(10)的两边同时左乘振型函数Φ( ) x,y，然后在整个板平面内进行积分，最后整理可以得到B1的振动方程

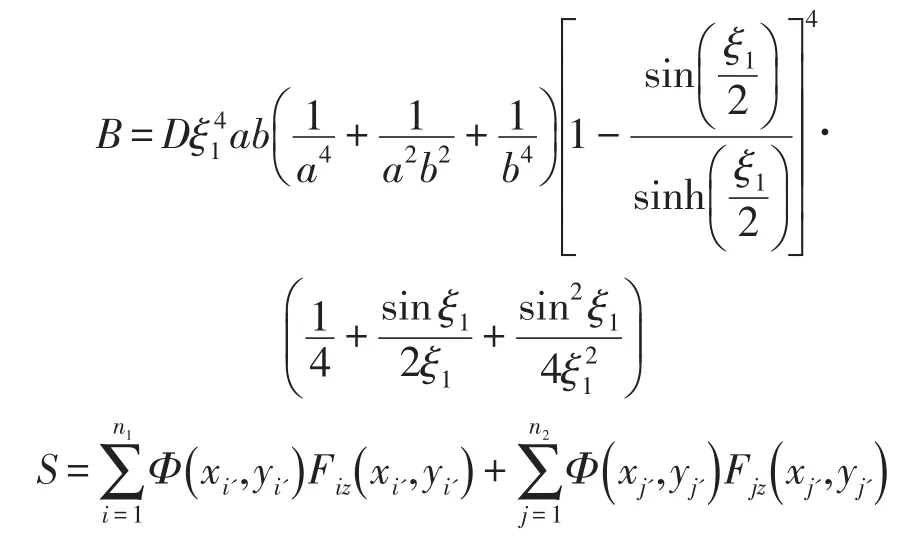
1.5系统的振动微分方程

综合系统的刚体运动和中间质量的弹性振动，可以得到整个系统的动力学方程，可以写为

P是非线性项，包含了弹性力、阻尼力以及冲击力的部分。

2　工程算例分析

2.1系统参数及隔振器安装

上层机组选择船舶用4135 G柴油机，其主要参数：质量m2=870 kg，长为1.205 m，宽为0.777 m，高度为1.198 m；中间质量的主要参数：密度为7 800 kg/m3，E=2.1×1011N/m2，μ=0.3，质量m1=522 kg，长为1.5 m，宽为1.0 m，厚度为44.6 mm。隔振器个数：n1=6，n2=4，其分布位置如图2和图3所示。

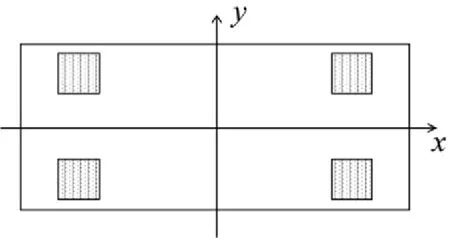
图2　B1上表面隔振器分布示意图

图3　B1下表面隔振器分布示意图

2.2冲击激励

0

0.009

t>0.022 5 s为冲击后阶段，系统的初位移和初速度为冲击阶段0.022 5 s的位移和速度，从0.022 5 s开始，系统作自由振动。

2.3冲击响应计算与分析

根据前面建立的系统动力学方程，可以求出系统在冲击载荷作用下的动力学响应，如表1所示。

对比有限元软件和数值计算方法计算的响应，可以看出最大误差为4.05 %，最小误差为1.55 %，即相对误差比较小，故可以说明建模理论是合理的。

根据有关文献[9]，中间质量第2阶及以上高阶弹性模态对系统冲击响应的影响要远远小于第1阶模态。因此，计算时只考虑了中间质量的第1阶模态，从表1中可以发现中间质量简化为刚体时的系统冲击响应，与考虑中间质量的弹性变形时相比较，最大误差可以达到11.93 %，可以说明中间质量的弹性对系统动力学特性有一定影响。

在考虑中间质量弹性振动的前提下，计算了线性隔振器系统的冲击响应，并和非线性隔振器的冲击响应进行对比，从表1中可以看出最大误差为9.46 %，故非线性隔振器对双层隔振系统的冲击响应有一定的影响。

表1　系统最大冲击响应

若中间质量的弹性与隔振器的非线性均不考虑时，计算得到系统的冲击响应与这两方面因素均考虑时的结果对比，最大误差可以达到22.30 %，故可以说明，在双层隔振系统中，同时考虑隔振器刚度非线性和阻尼非线性，以及中间质量的弹性时，数值更为精确。

3　结语

以多体动力学理论、动态子结构方法为基础，同时考虑中间质量的弹性和隔振器刚度与阻尼的非线性，建立了一个弹性双层隔振系统的动力学模型。通过工程算例分析，求出系统在冲击激励下的响应，并将其结果与有限元计算结果相比较，证明了所建力学模型的正确性与合理性。在此基础上进一步分析了中间质量的弹性和隔振器的非线性对双层隔振系统冲击响应的影响，可以看出当同时考虑中间质量的弹性和隔振器刚度以及阻尼的非线性时，计算所得到的冲击响应数值更精确。但是在工程实践中，精度往往不是唯一的目标，还要考虑复杂程度、工程效益等方面，所以还要根据实际情况进行选择。有关结论可以为隔振系统的设计和计算，提供一定的参考。

参考文献：

[1]李红钢，彭旭.具有刚度非线性双层隔振系统冲击响应数值分析研究[J].噪声与振动控制，2007，27（1）：21-26.

[2]商孝鹏.舰船机电设备非线性抗冲击理论建模和实验研究[D].上海：上海交通大学，2005.

[3]曹利，冯奇，张乐乐.双非线性隔振器的双层隔振系统模型的建立[J].噪声与振动控制，2008，28（2）：1-3.

[4] Wang Zhigang, Feng Qi, Wang Yu. Dynamic modeling and response analysis to impact of elastic floating raft system [J]. Journal of Ship Mechanics, 2005, 9(6):113-125.

[5]洪嘉振.计算多体系统动力学[M].北京：高等教育出版社，1999. 63-74.

[6]汪玉，冯奇.舰船设备抗冲隔振系统建模理论及其应用[M].北京：国防工业出版社，2006：12-34.

[7]曹利，冯奇，温建明.钢丝绳隔振器动态非线性阻尼模型的改进[J].石家庄铁道学院学报（自然科学版），2007，20 （3）：24-27.

[8]曲维德，唐恒龄.机械振动手册(第2版)[M].北京：机械工业出版社，2000：163-245.

[9]汪月，蒋丰.基础与阀体弹性对双层隔振系统冲击响应的影响[J].噪声与振动控制，2014，34（6）：37-40.

Modeling for an Elastic Double-stage Vibration Isolation System with Nonlinear Shock Absorbers

HAN Xiu-pin , JIANG Feng
( School of AerospaceEngineeringandApplied Mechanics, Tongji University, Shanghai 200092, China)

Abstract:Based on multi-body dynamics theory and dynamic substructure method, with the elasticity of the medium mass, nonlinear stiffness and nonlinear damping of the vibration isolators considered, the dynamic model of an elastic double-stagevibration isolation system wasestablished. Program calculation wasdonefor themodel and itsshock response wasobtained. Theresultswerecompared with thefiniteelement calculation results, and thecorrectnessand rationality of the established mechanical model were proved. On this basis, the influence of the elasticity of the medium mass and the nonlinearity of thevibrationisolatorsontheshock responseof thedouble-stagevibrationisolationsystemwasanalyzed.

Key words:vibrationandwave; double-stagevibrationisolationsystem; elasticplate; nonlinear; shock response

通讯作者：蒋丰，男，高级工程师，硕士生导师。E-mail:jiangfeng@tongji.edu.cn

作者简介：韩修品(1990- )，男，山东菏泽人，硕士生，主要研究方向为动力学建模与优化。

收稿日期：2015-09-18

文章编号：1006-1355(2016)02-0031-04

中图分类号：TB123

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.007