Holmes型Duffing系统动力学特性仿真及实验

孙方旭，刘树勇，何其伟（海军工程大学动力工程学院，武汉430033）



Holmes型Duffing系统动力学特性仿真及实验

孙方旭，刘树勇，何其伟
（海军工程大学动力工程学院，武汉430033）

摘要：针对混沌研究中缺乏可进行有效可重复性实验混沌振动平台问题，设计混沌振动实验台架并开展实验研究。建立近似于在双势阱中粒子运动的数学模型，并分析系统动力学特性，观察到系统出现的周期解和混沌解。利用系统响应随参数变化的分岔特性，得到系统混沌参数区。在实验研究中，进一步确定混沌参数区间，并观察到了Holmes型Duffing系统中初值敏感性现象以及在通往混沌过程中出现的对称破缺分岔和倍周期分岔现象。

关键词：振动与波；混沌实验；Duffing系统；双势阱；分岔

目前针对混沌现象的实验研究主要集中在三个领域：高速旋转机械、柔性体结构以及非线性电路。其中，梁山、郑剑等[1]通过两自由度非线性隔振系统模拟汽车悬架系统，并进行实验研究，系统通过伺服电机加载激励，以空气弹簧作为非线性元件，将实验结果和仿真结果进行比较，揭示该系统运动特性。刘凌，苏燕辰等[2]通过改进Lorenz系统，建立一种新的混沌系统并通过仿真分析该系统动力学特性，通过振荡电路系统实现了该类混沌系统，振荡电路主要由运算放大器、模拟乘法器、线性电阻、电容等组成。张雨、任成龙等[3]对汽车悬架系统中非线性振动情况进行研究，讨论了在特定激励下导致其混沌振动的可能性。Shi Peiming、Liu Bin等[4]分析谐波激励下一类扭转振动系统全局动力学特性，通过Melnikov方法分析该系统出现的混沌振动现象，并进一步进行数值仿真，通过实验观察到该系统通过倍周期分岔走向混沌的道路，该研究可以指导路面机械的结构设计。张小龙、东亚斌[5]对Duffing隔振系统的力传递率及跳跃现象进行理论分析。在上述文献中，针对Duffing系统的机械振动实验研究相对很少。

1　全局动力学特性研究

Duffing方程中，当α1<0,α2>0时，此类型被称为Holmes型Duffing方程。当激励为0时Holmes型Duffing方程对应的保守系统势能曲线如图1所示。

可以直观地看到，图1中保守系统存在双势阱，其存在两个稳定平衡点和一个不稳定平衡点，故Holmes型Duffing系统在较小的激励下就能产生混沌现象。这种混沌现象被归结为在两个平衡点之间的跳跃。

图1　方程x¨+δx. -x+x3=0势能曲线

典型Holmes型Duffing系统如图2所示。图2中一端带质量块的有阻尼弯曲梁在自由端受到磁力作用，同时固定端受到框架运动带给它的惯性力，其运动模式近似于在双势阱中运动的粒子，可以用如下方程描述

其中δ为无量纲阻尼；ω为驱动频率；A为无量纲激励力幅值。系统动力学行为受这些参数的影响。

图2　双势阱振动模型

式（1）中取δ=0.1，对此系统的动力学特性做初步研究。

通过延拓算法，求得频率从5 Hz逐渐增加到35 Hz情况下的系统全局分岔图，如图3所示，纵轴为输出响应幅值。当激励力幅值足够大时，在频率逐渐增加过程中，系统呈现出混沌解与周期解交错出现的特性，如图3（a）所示；而当激励幅值较小时，两个混沌参数区间变得很小，如图3（b）所示。将频率从35 Hz逐渐降低至5 Hz，通过延拓算法得出的全局分岔图如图4所示。

两种不同迭代方式的区别在于在特定频率处的初始条件不同，全局分岔图也呈现出很大的差异，说明此时Duffing系统的解和初始条件有很大的关系。以f =31 Hz为例，只改变系统的初值，可能得到如图5所示的两种截然不同的运动状态。具体而言，Duffing系统的吸引域可以通过胞映射方法得到直观验证。实际上，在实验过程中，也观察到了这种现象。

图3　全局分岔图

图4　全局分岔图

2　实验研究

2.1实验装置及仪器

根据混沌产生的必要条件，在混沌振动实验装置设计过程中，选择合适的非线性元件作为实验台的组成部分，主要利用元件的几何非线性、结构非线性、材料非线性或者电路的非线性等产生混沌。在此基础上，编制混沌识别程序对系统的动力学行为进行识别，通过定性分析技术对采集的时间历程图进行目视观察；利用相空间重构原理，获得实测时间序列相平面图，Poincaré截面图；利用定量分析方法提取信号的特征，进行Fourier分析得到信号频谱特征；计算信号分形维数和LE指数等。调节系统不同参数，观察到系统由周期进入混沌状态的途径。

基于以上考虑，双势阱单端磁吸式混沌振动装置如图6所示。装置由如下部分组成：激振器、支座、薄弹片、磁铁、小铁片、外部固定框架、固定弹片装置。实验采用的激光位移传感器型号为CD 33-30 NV，最大测试位移为±4 mm，最大允许误差为± 0.1 % F. S.；激光位移传感器与梁的距离为30 mm；梁的长与宽尺寸为155 mm×20 mm；磁铁的长、宽、高分别为11mm、6 mm、9 mm；磁铁顶端到底面高度为24mm；质量块重量为5g。

实验本质为正弦信号的慢速频率扫描实验，扫描频率范围为5 Hz～25 Hz，步长0.1 Hz，采样频率为2 kHz，数据采集时长为5 s。不断调节磁铁距中心线的距离、无激励时薄弹片距底端的距离，通过Labview观察输出响应。

图5　系统在不同初始条件下解的相图(A=400，ω=31)

图6　双势阱单端磁吸式混沌振动装置

2.2测定混沌区间

根据扫频调试，发现当激励频率大于10 Hz时，系统响应呈现丰富的动力学特征，因此，实验中将重点研究的频率范围限制在10 Hz到25 Hz之间。同时，考虑到功率放大器增益过大时，将对实验装置产生破坏性作用，因此增益范围确定为0～1.5 V。

当激振系统的增益为0.5 V时，不容易进入混沌状态，而是在单边势阱内处于周期1运动；当激振系统增益大于0.95 V时，系统的动力学行为非常丰富，可以产生包括混沌在内的不同振动模式。为了证实该结论，在增益为0.5 V条件下，改变激励频率从10 Hz到20 Hz，系统响应都为周期1模式。在频率为15 Hz到17 Hz之间，加入小的外部扰动，系统经过暂态过程后，落入势阱内，处于周期1状态。

为了观察系统的混沌响应并进一步证实以上规律的准确性，将激振系统的增益固定为1 V，由小到大增加系统的激励频率。当频率为5 Hz到10 Hz时，系统处于周期1状态；当激励频率大于10 Hz时，系统的响应特征非常丰富：在10 Hz～16 Hz时，产生混沌振动；在16. 6Hz时，系统出现周期2行为。在17 Hz到19 Hz频率范围内时，又产生并保持稳定的混沌运动。而在高频时，系统出现了切分岔，由混沌进入周期运动，19 Hz时，产生周期3运动；在19.4 Hz时，产生单势阱内的多周期运动。此外，还观察到了一些有趣现象，在23 Hz时，质量块穿越势阱壁垒在两个势阱之间来回运动，产生了大幅值的多周期振动；在30 Hz激励时，装置出现轰鸣声，该系统可能出现了共振现象。越过共振频率后，振子在右势阱内呈周期1运动模式。

通过实验，初步得到系统不同响应区域，以横坐标为激励频率，纵坐标为激励增益作出其示意图如图7所示。

由图7，当增益为1 V时，实验结果呈现出混沌、周期解交错出现的特性，这和仿真结果是相一致的。

2.3初值敏感性实验

激振器功率放大增益设为1 V，激励频率在22 Hz时系统状态为混沌状态，在23 Hz时为周期状态。那么在22 Hz～23 Hz之间的激励条件下，系统的状态是值得研究的。这种参数范围内，微小的改变能够导致系统响应产生巨大的变化，可以为弱故障信号混沌检测仪的研制、有害混沌的控制等提供最有效的参数区域。

激励频率在22 Hz时，以0.1 Hz为步长增加频率，系统整体的运动特性如表1所示。在实验中，发现22.2 Hz系统处于混沌态；而在22.3 Hz时，发生了有趣的现象，系统在经过2分钟左右的混沌运动后，进于周期状态，而且是在两个势阱之间大幅值振荡。

相反地，激励频率在23 Hz时，以0.1 Hz为步长减小频率。系统整体的运动特性如表2所示。在23 Hz时，系统为周期运动状态，但减小到22.2 Hz时，系统有时处于稳定的周期态，有时处于稳定的混沌态。多次实验表明，处于周期运动的概率大，而处于混沌态的概率小。

因此，22.2 Hz和22.3 Hz这两个频率点是值得重点关注的参数，因为系统沿着不同的方向改变参数时，在这两个点有多种可能的工作状态。在不同的初始状态时，系统可以进入不同的状态。这种性态可以为弱信号检测提供参考。例如，当检测信号中包含了早期弱故障信号时，混沌系统的运动特性将发生剧烈变化，从而给出明确的报警信号，预报故障的发生。

表1中说明了当频率以不同的方式改变时系统的运动情况。

图7　系统不同响应的参数区域示意图

表1　激励频率变化时系统动力学行为特征

2.4对称破缺分岔实验验证

另一方面，在实验中，还观测到了Duffing系统中当激励频率不断变化时，系统解出现对称破缺分岔、倍周期分岔并最终走向混沌的过程。

当激励增益为0.92 V，激励频率从25 Hz逐渐降低，通过相空间重构得出的相图见图8。

从图8中可以看到，当激励频率f =22.5 Hz开始出现对称破缺，由于系统产生对称破缺分岔必成对出现，在实验中，取激励频率为21.9 Hz时，通过给系统一个扰动改变初始条件，观察到了图8（e）和图8 （f）中成中心对称的两个对称破缺分岔相图。进一步降低激励频率，当f=21.5 Hz，系统产生了混沌运动，如图9所示。

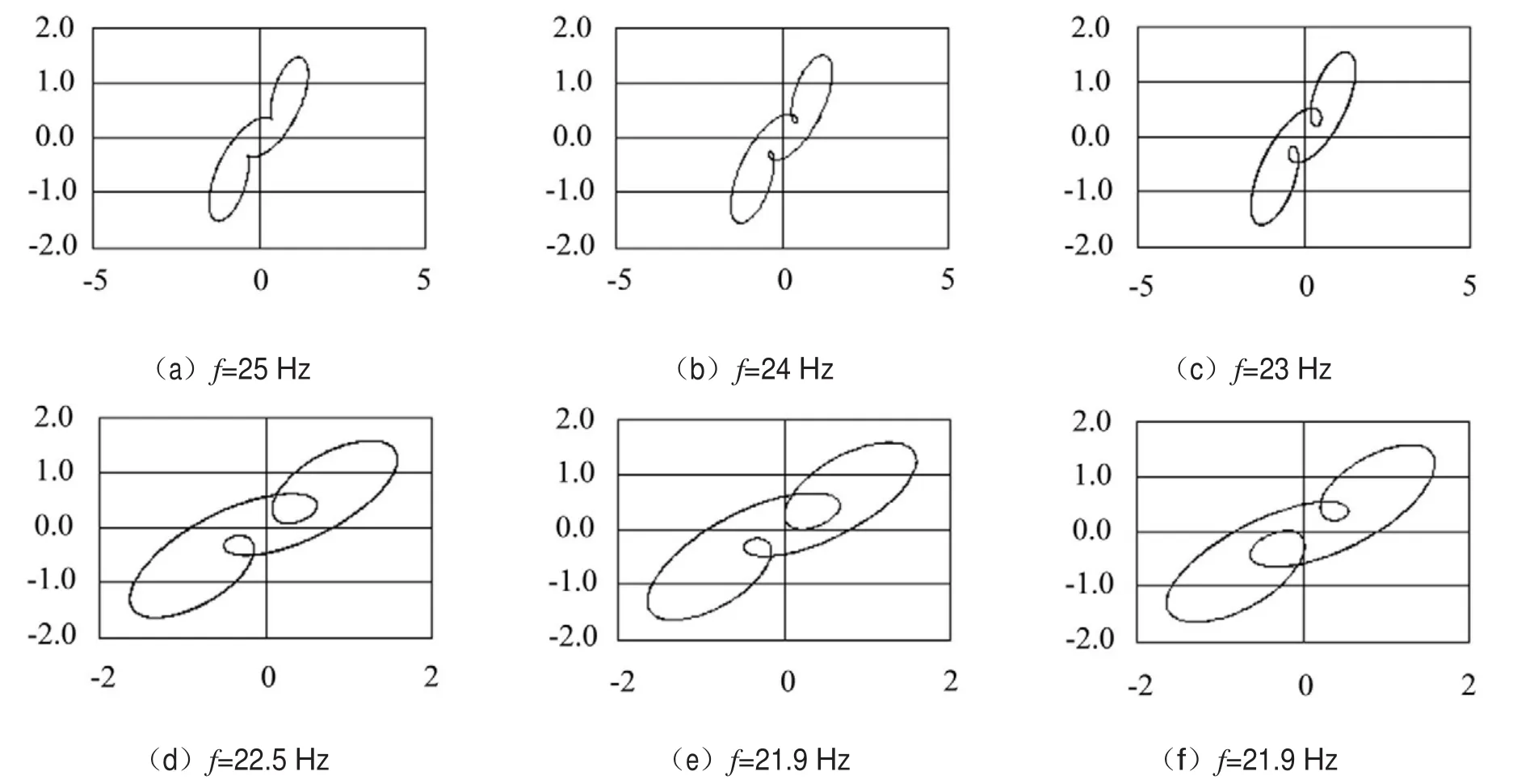
图8　激励频率改变时的相平面图

(3)基于组合结构的导纳参数模型，可以分析各子结构参数变化对耦合结构振动传递特性的影响规律，作为发动机舱声学设计的基础。

参考文献：

[1]李海飞.圆柱壳体结构振动特性分频段建模研究[D].西安：西北工业大学，2012.

[2] Ming R S, Pan J, Norton M P. The mobility functions and their application in calculating power flow in coupled cylindrical shells[J]. Journal of the Acoustical Society of America, 1999, 105(3):1702-1713.

[3]赵芝梅，盛美萍，陈永辉.板壳结构振动特性的等效机械导纳法[J].噪声与振动控制，2011，31(6)：20-23.

[4]杜功焕，朱哲民，龚秀芬.声学基础[M].南京：南京大学出版社，2001.

[5]盛美萍，王敏庆，孙进才.噪声与振动控制技术基础[M].北京：科学出版社，2001.

[6]郜立焕，唐晓阳，李言芝，等.齿数对齿轮泵流量脉动特性影响的分析[J].机床与液压，2011，39(6)：71-72.

[7]苏尔敦，王敏庆.梁板耦合结构振动功率流特性研究[J].噪声与振动控制，2009，29(4)：6-9.

Simulation and Experimental Study on the Dynamic Characteristics of the Holmes Duffing System

SUN Fang-xu , LIU Shu-yong , HE Qi-wei
( School of Power Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract:Currently, thereisthedeficiency of repeatablechaotic vibration experimentsin chaotic study. In thispaper, a chaotic vibration experiment platform was designed and researched. The model of approximate particle motion in double potential well was established and its dynamic characteristics were analyzed. As a result, the periodic solutions and chaotic solutions were observed. In experimental study, parameter interval of the chaos was determined. In addition, the sensitivity of initial value in Holmes Duffing system was observed. Symmetry breaking bifurcation and period doubling bifurcation wereall observedintheDuffingsystem.

Key words:vibrationandwave; chaoticexperiment; Duffingsystem; doublepotential well; bifurcation

作者简介：孙方旭（1992-），男，内蒙古赤峰市人，硕士研究生，主要研究方向为噪声与振动控制。E-mail:sunfx2013@hotmail.com

基金项目：国家自然科学基金资助项目（51179197）

收稿日期：2015-08-14

文章编号：1006-1355(2016)02-0017-04+26

中图分类号：O322

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.004