不规则结构导纳参数建模方法研究

张武林，盛美萍（.西北工业大学航海学院，西安70072；2中国飞行试验研究院飞机所，西安70089）



不规则结构导纳参数建模方法研究

张武林1, 2，盛美萍1
（1.西北工业大学航海学院，西安710072；2中国飞行试验研究院飞机所，西安710089）

摘要：复杂结构都是由各种不规则子结构组成，一般采用动力学试验或者仿真分析方法获得其振动特性。而为了快速获取复杂结构振动响应规律，指导结构声学设计，常需开展子结构参数化建模。导纳反映了结构振动响应特性。以导纳作为等效建模基本参数，对发动机中泵结构建立矩形空心梁等效模型，通过改变激励位置及材料参数，并结合试验测试结果，证明所建立模型的正确性及建模方法的适用性。

关键词：振动与波；导纳；参数化建模；子结构

组合结构都是由各子结构通过一定的耦合方式连接而成。分析各子结构的振动特性以及子结构之间的耦合特性，将有助于研究子结构间的振动传递特性，在此基础上获取振动传递规律，还将对结构的声学设计具有一定的指导意义。

开展结构的导纳参数建模，可以有效地预估结构在任意激励下的振动响应，并且基于参数化模型可以实现复杂结构振动传递的最优化设计。目前，参数化建模已在典型结构如梁、板、壳及其耦合结构上得到了广泛应用[1–3]，而复杂结构如何建立合理有效的等效参数化模型，及不同激励条件下各结构参数变化对耦合模型振动传递特性有何影响，对于此类问题的研究相对较少。对于实际中的子结构，多数已不再是传统意义上的典型结构，同时还存在着与其相连子结构之间的复杂耦合作用，能否对其进行准确的参数建模将会对获取结构振动传递特性产生非常重要的影响。以发动机中的泵结构为研究对象，讨论不规则结构的导纳参数模型的建模方法，以期能够将该建模方法应用于解决工程实际问题。

在提出建模方法之前，首先对文中所用到的相关理论知识做一简单介绍。

1　相关理论

对于端点受简谐激励的弯曲振动梁，可以将激励载荷作为边界条件推导梁的强迫振动响应，当激励载荷作用于梁上任意一点时，可以将梁在激励位置处一分为二，如图1所示，在激励位置处联立位移、转角、剪力、弯矩等连续条件，计算获得其振动特性。

设弯曲振动梁的空间分布形式为[4, 5]

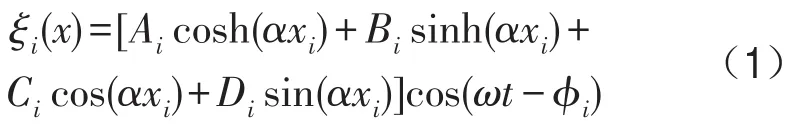
其中i=1，2，分别对应于梁1与梁2。

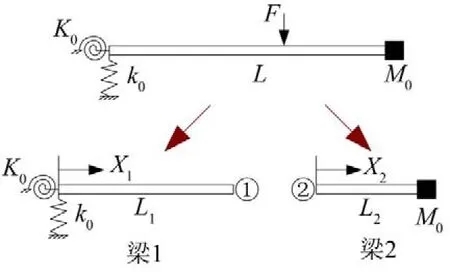
图1　一端弹性、一端约束附有集中质量的中间受激弹性梁

梁1左端边界条件与梁2右端边界条件分别为

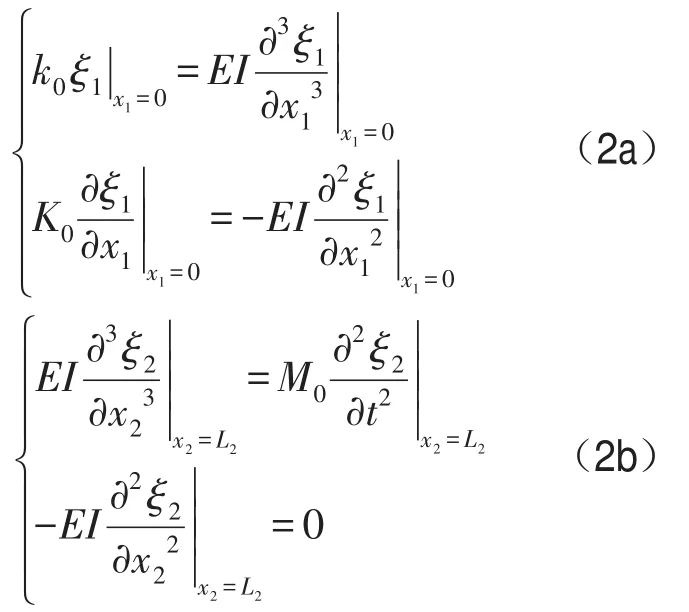
在梁1与梁2连接位置处，位移相等，转角相等，弯矩相等，剪力之差等于外载荷，即

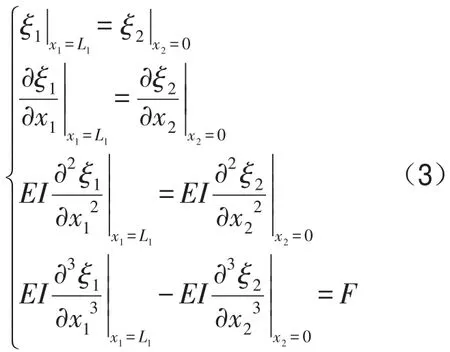
当梁中间受到弯矩激励时，可以得到类似于式（3）的关系式。联立上述的边界条件，就可以得到梁上任意一点处的结构振动响应。

分段梁模型的处理方法，将激励载荷作为分界点处的连续条件，很好地将梁弯曲振型的推导方法应用于任意位置点激励下弯曲振动响应的计算，为梁的受迫振动分析提供了一个简单直接的计算方法。

2　泵结构振动特性分析

泵结构为发动机的主要动力源结构，由螺栓连接于发动机上，主要用于汲取外部燃料以满足发动机工作需要。泵顶端及底端安装法兰为近似矩形，中间部分外轮廓为不规则多边形，而其内部则为沿泵轴向的活塞空腔，泵横截面示意图如图2所示，图中虚线表示顶端与安装法兰截面，泵高度h=20.0 cm。分析其结构特点可以看出，该泵为不规则结构。

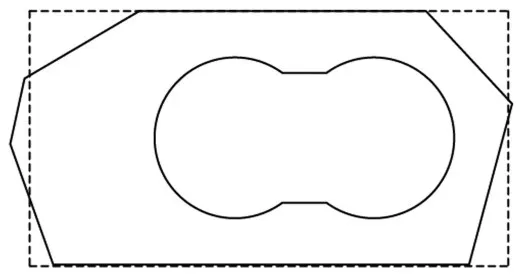
图2　泵结构截面示意图

对于非规则结构，无法直接从理论上获取其振动特性。泵结构尺寸相对较小，结构刚度较大，在研究频率范围内（200 Hz～3000 Hz），自由边界条件下无振动模态，不易激起结构的振动响应，不利于开展结构的导纳参数建模；而在发动机正常工作情况下，泵通过四角处的螺栓将其固定于发动机的前隔板上，为保证工作时的稳定性及安全性，此安装刚度较大，故这里首先借助有限元对固支边界条件下的泵结构进行振动特性分析，计算得到泵的前两阶振型如图3所示，各阶固有频率及对应振型描述见表1。

图3　固支边界下泵的前两阶振型

表1　固有频率与对应振型描述

泵受到的主要激励载荷是入口处作用于壳体的径向激励力[6]，图3中结构左侧圆形缺口即为泵的入口。仿真计算得到入口处点力激励下的输入导纳如图4所示。

由图4可以看出，在研究的频率范围内，泵共有两阶模态峰值，第1阶峰值较大，其对应振型平行于激励方向；第2阶振型与第1阶近似正交，在所研究激励下，对输入导纳的贡献较小；所以在对泵等效参数建模时，应主要考虑第1阶振型。

图4　入口点力激励下的输入导纳

3　泵导纳参数模型的建立与验证

由上述分析结果可知，第1阶峰值对泵及泵与发动机的耦合结构的振动特性起主要作用，而第1阶峰值所在频段内输入导纳的变化特性与梁的弯曲振动相似，故可以考虑采用梁模型对泵进行导纳参数建模。

泵为非规则结构，等效为梁模型时，其部分参数的确定是一个复杂过程。观察其结构特点，宽度（垂直激励方向）与厚度（平行激励方向）的比值接近2:1，且为中空结构，联系其振型特点，可以考虑将泵等效为矩形空心梁模型，取空心梁截面的外尺寸与泵的外尺寸近似相等，其余等效参数的获取流程如图5所示。

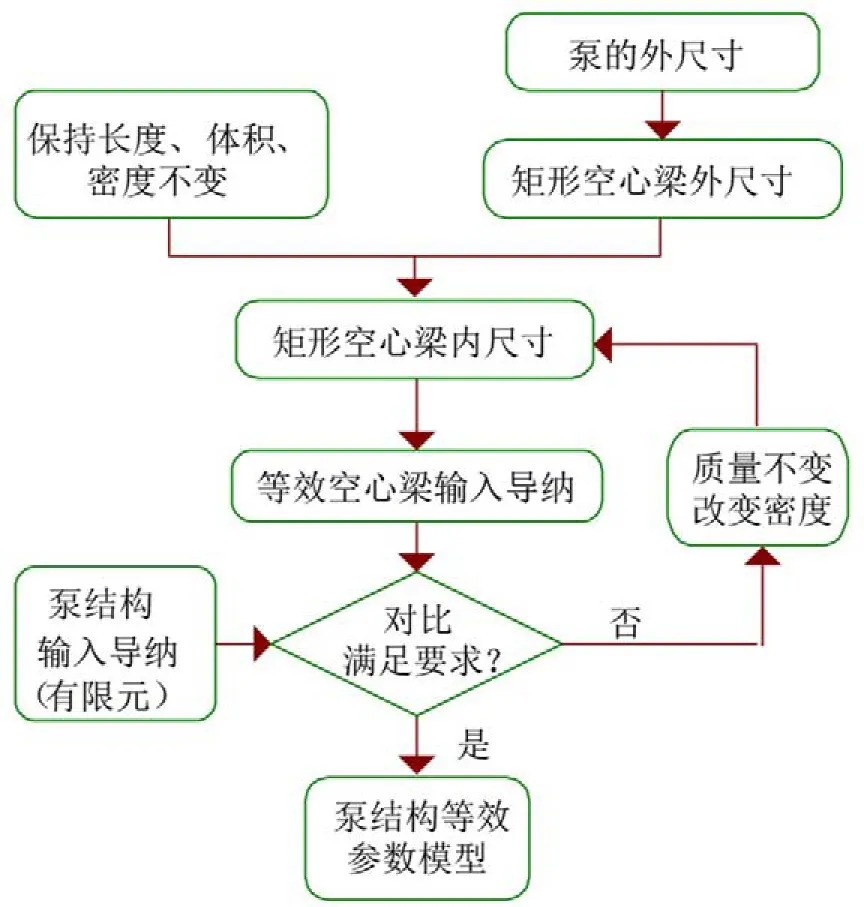
图5　矩形空心梁等效参数的获取流程

基于上述方法第一次得到的空心梁内尺寸计算泵的输入导纳时，所得结果会有一定误差，可对内尺寸多次修正，得到最佳等效模型，在对内尺寸修正时，需保证泵的质量不变，即密度除以体积变化倍数，基于所得参数计算获取等效梁模型的输入导纳如图6所示。

图6　等效模型与泵结构输入导纳对比

由图6可以看出，等效模型在研究频段内具有较好的近似效果；同时，对于该等效模型，其正交方向上弯曲振动的第1阶固有频率为2736 Hz，与有限元仿真结果2684 Hz的误差不足2%，等效模型近似程度较高，所以当泵所受的激励载荷方向发生偏移时，只需将激励载荷正交分解，直接采用矩形空心梁进行导纳计算，无需再次等效。

子结构的导纳参数化建模是指当原结构参数发生变化时，只需改变等效模型对应参数，即可近似获取原结构导纳特性的一种建模方法。

依次改变等效模型的载荷激励位置（距离安装底面14.2m→7.5cm）、弹性模量（70 GPa→97 GPa）、材料密度（2700kg/m3→4000kg/m3），计算获取导纳参数模型的输入导纳，并与有限元计算结果进行对比，如图7至图9所示。

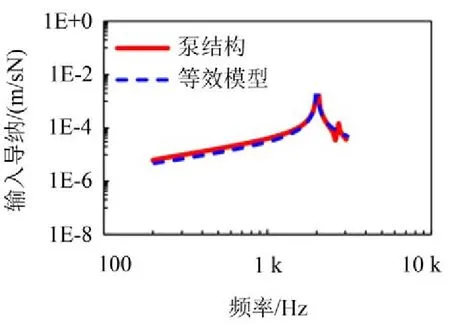
图7　改变载荷激励位置后输入导纳对比

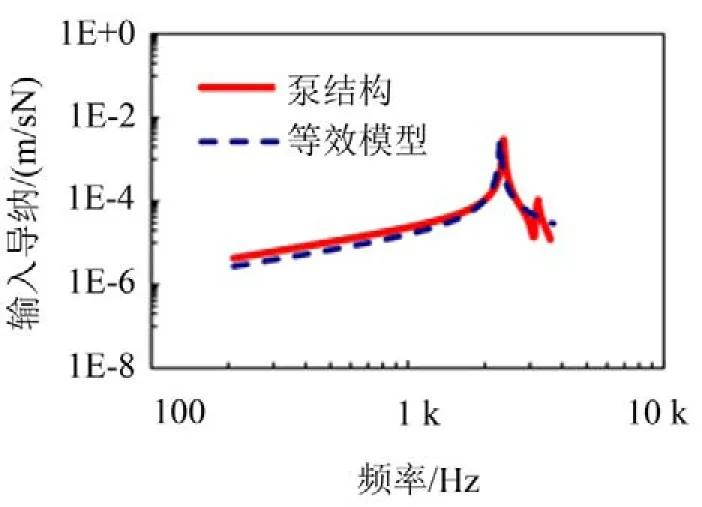
图8　改变弹性模量后输入导纳对比

两个激励位置位于入口周边，距离安装底面最远与最近处，而变化后的材料参数则取自发动机其他子结构的材料参数。分析各图可以看出，激励位置变化只影响峰值大小，弹性模量变大，固有频率上移，材料密度变大，固有频率下移；当在小范围内改变上述参数时，所建立的导纳参数模型在所研究频段内仍具有较好的等效效果。

图9　改变材料密度后输入导纳对比

4　耦合模型建立与验证

发动机圆隔板在(r1,θ1)与泵结构耦合，泵受到F0的作用，其垂直于泵的轴向且沿隔板径向，隔板受到轴向力F2作用，子结构与圆隔板耦合模型示意图如图10所示。

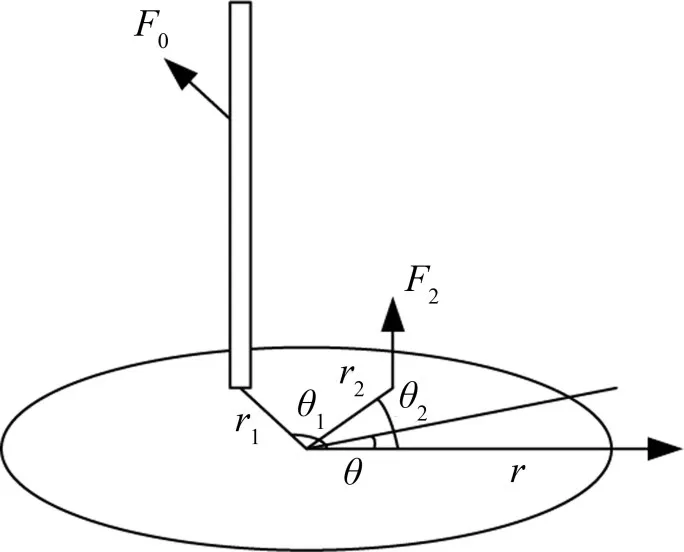
图10　子结构与隔板耦合示意图

在以梁的弯曲振动为主要考虑对象的梁板耦合系统中，耦合弯矩为主要耦合作用力（已由有限元模型验证），下面基于此讨论子结构与隔板耦合系统的导纳计算方法。由子结构导纳法，可以得到梁与圆板在耦合点处的角速度

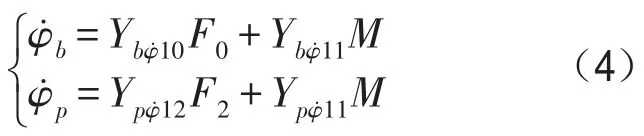
式中角标b对应于梁，角标p对应于隔板，角标0对应于梁上激励点，角标2对应于圆板上激励点，角标1对应于梁与圆板的耦合点，M对应于耦合弯矩，Y对应于梁与隔板的传递导纳。

在连接位置处，子结构边界保持连续[7]，对于梁与圆板耦合连接，在耦合位置处角速度相等，即，由式（4）进一步可以得到耦合弯矩

求解出耦合弯矩后，就可以得到梁上任一点处的速度响应

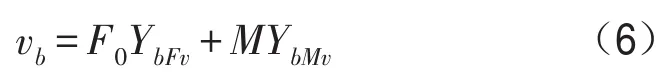
圆板上任一点处的速度响应

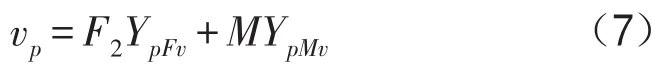
对于由多个子结构连接形成的耦合模型，采用上述计算方法，可以得到耦合矩阵方程

其中Y表示各子结构传递导纳形成的导纳矩阵，F表示耦合载荷矩阵，V表示外载荷引起的对应子结构的响应矩阵。

将矩形空心梁与发动机的导纳参数模型耦合连接，计算得到耦合模型的输入导纳，并与试验测试结果对比，如图11所示。

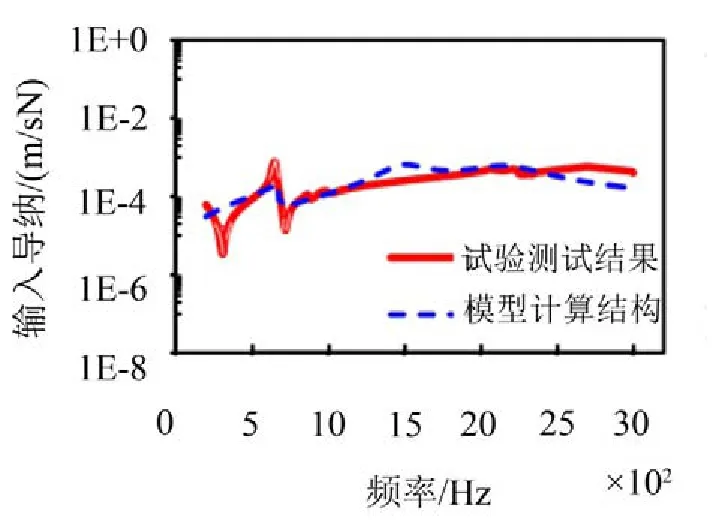
图11　耦合结构输入导纳对比

由图11可以看出，理论计算值与试验测试值变化趋势保持一致，除部分频点外，二者差值较小。

经过上述对独立子结构模型以及耦合模型的验证可知，在研究频率范围内，导纳参数模型具有较高的等效精度，进一步证实了该建模方法的有效性与正确性。当改变耦合模型中任一子结构的参数时，基于耦合模型的导纳参数化模型，可以快速计算得到模型的振动传递规律以及子结构参数对耦合模型上目标位置处振动响应的影响特性，所以，建立组合结构的导纳参数模型为耦合结构振动特性的获取及结构的声学优化设计奠定了基础。

5　结语

(1)以发动机中的泵结构为研究对象，探索了非规则结构导纳参数模型的建模方法，通过改变结构的激励位置及材料参数，并对比有限元计算结果，证明了该建模方法的可行性及所建立导纳参数模型的正确性。

(2)该方法已成功地运用于获取发动机其他子结构的导纳参数模型；导纳参数模型的建立，将慢而复杂的有限元计算转化为耦合结构的导纳参数计算，大大简化了振动传递的计算过程。

传输高效区和低效区。该划分方式对行波解和非行波解均有效，可以全面地刻画有限长周期结构的能量传输特性。

(3)在某些情况下，非行波解的能量传输效率可以高于行波解，换句话说，在有限周期结构中，传输效率最高的模式未必是行波模式，因此在应用周期结构原理设计隔振器时，需要考虑非行波模式对能量传输的贡献。

参考文献：

[1] Brillouin L. Wave propagation in periodic structures:electric filters and crystal lattices. secord edition[M]. New York:Dover Publications, 1953.

[2]吴代鸣.固体物理基础第2版[M].北京：高等教育出版社，2015.

[3] Mead D J. Wave propagation in continuous periodic structures:Research contributions from Southampton, 1964-1995［J］. Journal of Sound and Vibration, 1996, 190(3):495-524.

[4]陈斌，黄修长.周期结构振动控制研究现状[J].噪声与振动控制，2011，31(5)：37-41.

[5] Hussein, M I, Leamy M J, Ruzzene M. Dynamics of phononic materials and structures:historical origins, recent progress, and future outlook[J]. Applied Mechanics Reviews, 2014, 66(4):040802.

[6] Bondaryk J E. Vibration of truss structures[J]. Journal of the Acoustical Society of America, 1997,102(4):2167-2175.

[7]黄修长，徐时吟，华宏星，等.梁周期结构动力学特性和隔振性能[J].上海交通大学学报，2013，47(2)：173-179.

[8] Xiao Y, Wen J, Yu D, et al. Flexural wave propagation in beams with periodically attached vibration absorbers:Band- gap behavior and band formation mechanisms[J]. Journal of Sound and Vibration, 2013, 332(4):867-893.

[9]尹剑飞，温激鸿，肖勇，等.基于高级统计能量分析的周期加筋板振动特性研究[J].物理学报，2015，(13)：182-191.

[10] Mei J, Ma G C, Yang M, et al. Dark acoustic metamaterials as super absorbers for low-frequency sound [J]. Nature Communications, 2012, 3(2):132-136.

[11] Yan Y, Cheng Z, Menq F, et al. Three dimensional periodic foundations for base seismic isolation[J]. Smart Materials & Structures, 2015, 24(7):075006.

[12] Wang P, Casadei F, Shan S C, et al. Harnessing buckling to design tunable locally resonant acoustic metamaterials [J]. Physical Review Letters, 2014, 113(1):014301.

[13]温激鸿，王刚，郁殿龙，等.声子晶体振动带隙及减振特性研究[J].中国科学：E辑，2007，37(9)：1126-1139.

[14]刘启能，刘沁.固-固有限周期声子晶体中SH波全反射隧穿的机理[J].计算力学学报，2014，31(1)：61-66.

[15]臧献国，于德介，姚凌云.响应表面法在结构噪声优化中的应用研究[J].噪声与振动控制，2009，29(4)：116-119.

[16] Mead D J. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling[J]. Journal of Sound and Vibration, 1973, 27 (2):235-260.

Study on Mobility Parametric Modeling of Irregular Structures

ZHANG Wu-lin1, 2, SHENG Mei-ping1
( 1. School of MarineScienceand Technology, Northwestern Polytechnical University, Xi’an 710072, China; 2.Aircraft Research Institute, ChinaFlight Test Establishment, Xi’an 710089, China)

Abstract:Complex structuresconsist of variousirregular sub-structures. Their vibration characteristicscan usually be obtained by dynamic test and simulation analysis. In order to quickly obtain thevibration responseof thecomplex structures and guide acoustic design of the structures, parametric modeling of sub-structures is necessary. In this paper, the mobility, which can reflect thestructural vibration responsecharacteristics, wasused asthebasic parameter to build an equivalent boxbeam model of engine pumps. By changing the excitation position and material parameters and combining with the test results, thecorrectnessandapplicability of theparametricmodel wereverified

Key words:vibrationandwave; mobility; parametricmodeling; sub-structure

作者简介：张武林（1987-），男，河南省商丘市人，助理工程师，主要研究方向为噪声与振动测试及其控制。E-mail:595172061@qq.com

收稿日期：2015-09-09

文章编号：1006-1355(2016)02-0027-04+45

中图分类号：TB123

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.006