基于局部振动测试的约束子结构模型修正方法

郭俊龙　马立元　李　辉　李世龙

军械工程学院，石家庄，050003

基于局部振动测试的约束子结构模型修正方法

郭俊龙马立元李辉李世龙

军械工程学院，石家庄，050003

针对大型复杂结构模型修正中待识别参数过多、修正效率低等问题，提出一种基于局部振动测试的约束子结构模型修正方法。首先，利用子结构部分的振动测试响应构造约束子结构，从而将子结构从整体结构中隔离出来，形成独立简单的结构，有效地隔绝整体结构对子结构的影响。然后，基于构造的约束子结构响应数据，直接对待修正的目标子结构进行模型修正。最后，以一个T形钢管焊接结构和某发射台骨架为例，对所提方法的有效性进行了验证分析。结果表明，该方法不仅能够减少待识别参数，简化修正过程，而且修正效率及精度也较高，为大型复杂结构的模型修正提供了一种新思路。

振动测试响应；约束子结构；模型修正；目标函数

0　引言

近年来，随着装备制造业的迅猛发展,一些大型机械结构形式与功能日趋复杂,工程的规模也越来越大，然而，由结构损伤所导致的一些突发性毁坏事件也越来越多,因此,对复杂机械结构损伤识别方法的研究刻不容缓。

基于模型修正的损伤识别是结构损伤识别领域的一个研究重点。Imregun等[1]、Mottershead等[2]分别详细阐述了有限元模型修正方法。Friswell等[3]对有限元模型修正理论及其应用进行了详细阐述。Fritzen等[4]提出了一种基于灵敏度模型修正的损伤识别方法，用于定位并量化一块铝板内存在的损伤。Perer等[5]通过最小化数值模型和试验模型在频率及模态振型之间的差异来检测一个三维框架节点损伤。张纯等[6]提出了正则化模型修正方法，得到了较好的修正效果。钟儒勉等[7]提出了一种基于多尺度的模型修正方法，对一结合梁斜拉桥进行了模型修正，有效识别了损伤。李世龙等[8]提出一种大型复杂结构损伤识别的两步法，首先运用模型修正方法对结构进行模糊识别，然后运用模态柔度曲率差法精确定位损伤，并通过一个发射台骨架验证了该方法的有效性。上述方法在模型修正过程中，都是对整体结构进行修正，需要识别大量参数，如果能针对整体结构中关心的子结构进行模型修正，则可以减少待识别参数，并大大提高修正效率。

在对子结构部分进行模型修正时，需要考虑整体结构对子结构的影响，特别是当子结构的边界条件比较复杂时，直接对子结构进行模型修正难度较大。侯吉林等[9]提出约束子结构的概念，通过约束和限制整体结构中子结构部分的边界响应，并利用子结构位置的动态信息构造约束子结构的动态信息，将子结构从整体结构中隔离出来，形成独立简单的结构，从而有效地隔绝整体结构对子结构的影响。

本文在约束子结构概念的基础上，提出一种基于局部振动测试的约束子结构模型修正方法，利用子结构部分的振动测试响应构造约束子结构，并利用构造出的振动响应对子结构进行模型修正，从而大大提高了模型修正效率。

1　结构响应矩阵

1.1单自由度结构响应矩阵

针对单自由度结构，在初始状态为0的情况下，其响应y(t)可由杜哈梅积分计算得到，即

(1)

式中，p(τ)为作用的激励；h(t)为脉冲响应函数。

对式(1)在s个时刻内进行离散，可得

(2)

Y=H P

(3)

(4)

式中，H为由脉冲响应函数构成的s维下三角方阵，它的第i列向量为在第i时刻施加激励时结构的脉冲响应函数。

1.2多自由度结构响应矩阵

对一N自由度线性结构，在初始状态为0的情况下，在第j自由度施加单一激励，则第i自由度方向响应与单自由度情况类似，即

Yij=HijPj

(5)

式中，Yij为在第j自由度施加激励时，第i自由度方向的响应；Hij为在第j自由度施加激励时，第i自由度方向响应的脉冲响应函数矩阵；Pj为在第j自由度方向上施加的单一激励。

由于结构为线性结构，满足线性叠加原理，因此，在各自由度方向同时施加激励时第i自由度的响应Yi为

Yi=Yi1+Yi2+…+YiN

(6)

2　约束子结构响应矩阵的构造

针对所关心的子结构部分，由约束子结构思想，在子结构边界及内部布置一定数量的传感器，获得子结构边界及内部的振动测试响应，并通过推导约束方程计算约束子结构的响应。

2.1传感器布置

如果子结构边界有m个自由度，则需要布置m个传感器才能实现对子结构边界的约束，将这些传感器分别记为b1，b2，…，bm；为了准确得到约束子结构的内部响应，同时需要在子结构内部布置n个传感器，将这些传感器分别记为1，2，…，n。

2.2构造约束子结构响应

在子结构内部传感器方向分别施加激励Pi(i=1,2,…,n)，并将其记为内部激励Ps，即Ps=diag(P1,P2,…,Pn)，设此时引起的子结构内部和边界的响应分别为Yss和Ysb，对应的脉冲响应函数矩阵为Hss和Hsb，则有

Yss=HssPs

(7)

Ysb=HsbPs

(8)

(9)

(10)

式中，Yij为在第j自由度施加激励时第i自由度的响应。

在子结构边界传感器方向分别施加激励Pj(j=1,2,…,n)，并将其记为边界激励Pb，即Pb=diag(P1,P2,…,Pn)，此时引起的子结构内部和边界的响应分别为Ybs和Ybb，对应的脉冲响应函数矩阵为Hbs和Hbb。则有

Ybs=HbsPb

(11)

Ybb=HbbPb

(12)

(13)

(14)

式中，Yij为在第j自由度施加激励时第i自由度的响应。

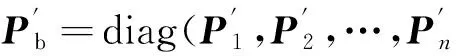
(15)

(16)

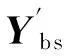
(17)

将式(15)代入式(17)右端并简单整理可得

(18)

同理：

(19)

所以

(20)

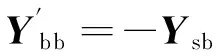
(21)

由式(7)和式(21)可得，在子结构内部激励和边界约束激励的共同作用下，所得子结构的响应为

(22)

将式(21)代入式(22)可得约束子结构响应为

(23)

矩阵Yss、Ysb、Ybs和Ybb都可由实测子结构的内部和边界响应得到，因此约束子结构的响应矩阵可由整体结构中子结构部分的响应矩阵求得。

3　约束子结构模型修正

得到约束子结构的响应之后，分别对约束子结构进行理论及实验模态分析，通过对比理论及实际模态参数进行模型修正。

本文首先采用ANSYS软件对约束子结构模型进行理论模态分析，之后采用江苏东华公司的DH5920动态信号测试分析仪及其配套软件对结构进行实验数据采集和模态分析。

模型修正时，将待修正的约束子结构部分分为n个单元，设修正因子集合μ={μ1,μ2,…,μn}，修正因子为单元实际弹性模量与理论弹性模量的比值。

由约束子结构的第i阶模态振型φi和刚度矩阵K定义结构第i阶模态应变能Ei为

则可定义目标函数如下：

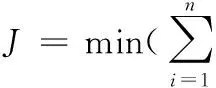
(24)

式中，ωi、ωoi分别为结构第i阶实际固有频率和理论固有频率；Ei、Eoi分别为结构第i阶实际模态应变能和理论模态应变能。

通过调整μ对式(24)进行最小化，得到修正因子后即可获得修正后的约束子结构模型。

由于约束子结构模型所含单元数目少，待修正的未知参数少，可采用MATLAB中的fminsearch函数进行优化。

4　实验验证

首先以一个T形焊接钢管为例，简要说明约束子结构构造过程，然后对某发射台骨架上易损伤的部位进行约束子结构模型修正。

4.1约束子结构振动响应的构造

T形焊接钢管结构及传感器布置方案如图1所示，其中，横管长0.4m，外径为60mm，内径为50mm，竖管长0.25m，外径为40mm，内径为30mm，材料弹性模量为207GPa，泊松比为0.27，密度为7800kg/m3，结构为瑞利阻尼，竖管为待构造约束子结构部分。T形钢管通过弹性绳悬挂于稳定刚架上，各自由度方向无约束。

图1　T形焊接钢管

为将子结构的边界响应限制为零，在子结构边界位置布置两个传感器b1和b2；同时，为体现子结构内部响应，在子结构内部布置4个传感器，编号为1～4。在子结构边界和内部激励的共同作用下，通过式(23)，可得出约束子结构响应。

理论约束子结构部分前4阶模态频率如表1所示，由奈奎斯特采样定理，采样频率选择20kHz，共采集500个点，采样时间为25ms。

表1　约束子结构理论模态频率

下面针对T形焊接钢管介绍约束子结构振动响应的构造过程。首先在6个传感器方向分别施加脉冲激励，激励通过力锤敲击的方式进行施加，激励点靠近传感器测点位置，激励方向控制与传感器测量方向一致。通过施加激励可得到6×6共36组测试数据，图2和图3分别为在1号传感器方向施加脉冲激励后子结构的边界和内部响应。

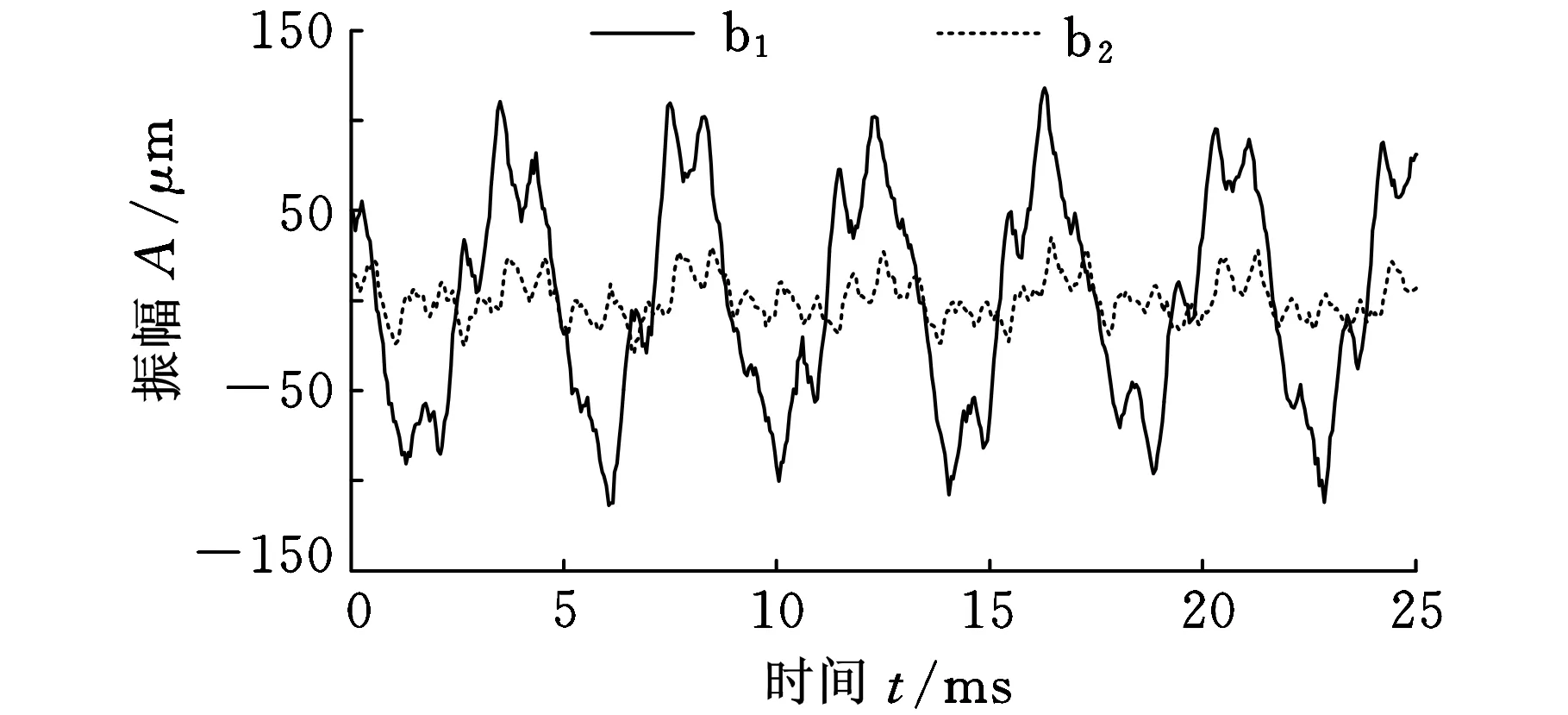
图2　子结构边界响应

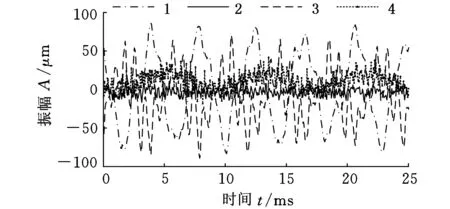
图3　子结构内部响应

按照式(9)、式(10)、式(13)和式(14)构造矩阵Yss、Ysb、Ybs和Ybb，并代入式(23)，即可得到约束子结构部分的振动响应。图4和图5即为计算得到的约束子结构边界和内部响应。

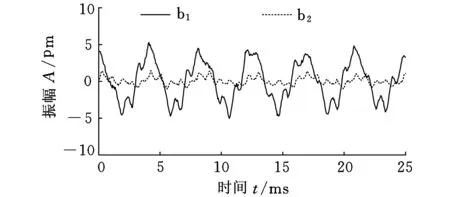
图4　约束子结构边界响应

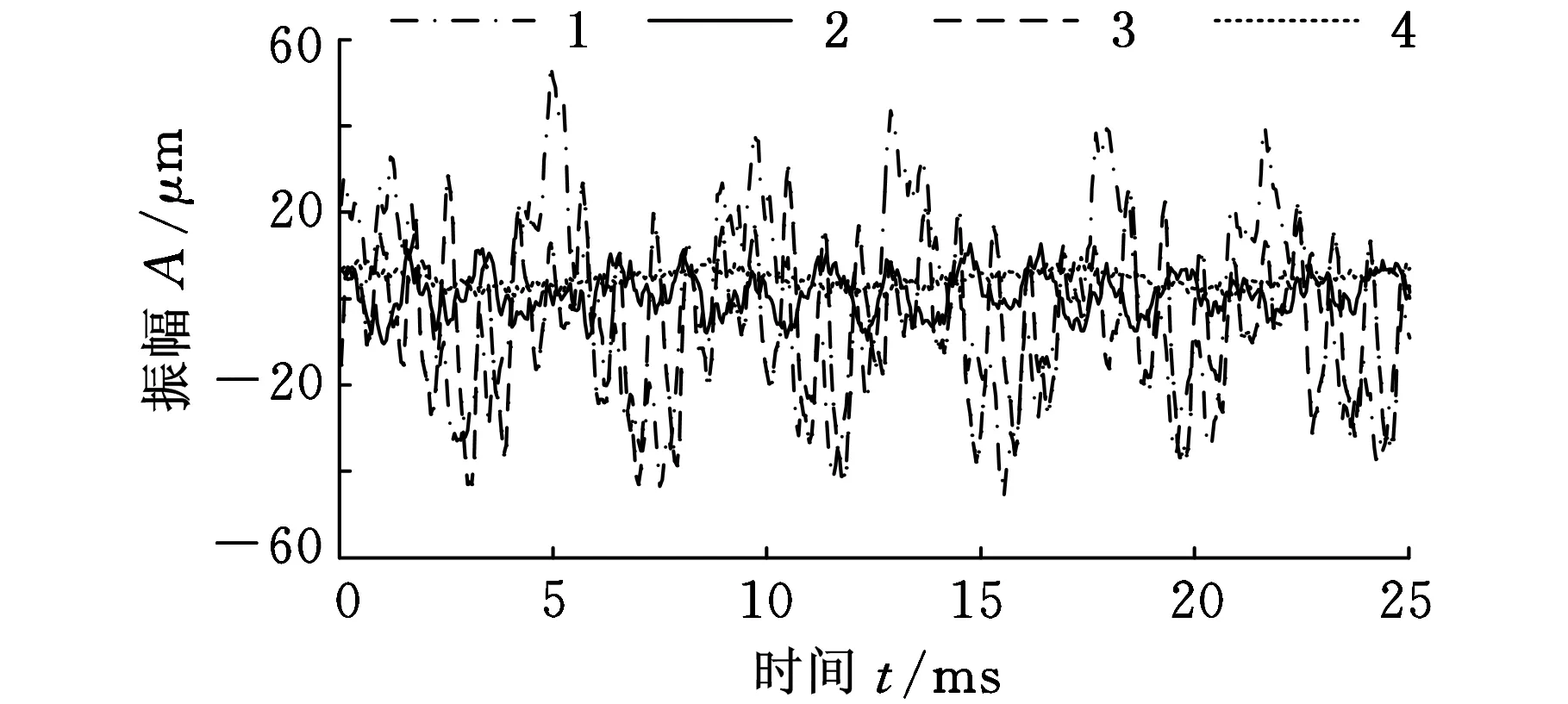
图5　约束子结构内部响应

图4中约束子结构边界响应最大值约为5 pm，远小于图2中的100 μm，因此可以近似认为子结构边界响应为0，即成功地限制了子结构边界响应，将子结构从整体结构中隔离出来，构造出约束子结构模型。因此图5中响应可近似认为是待构造约束子结构部分的响应。

利用有限元软件对子结构模型进行理论模态分析，并将构造的约束子结构响应数据导入DHMA模态分析软件中进行分析，得到的理论及实测模态频率如表2所示。

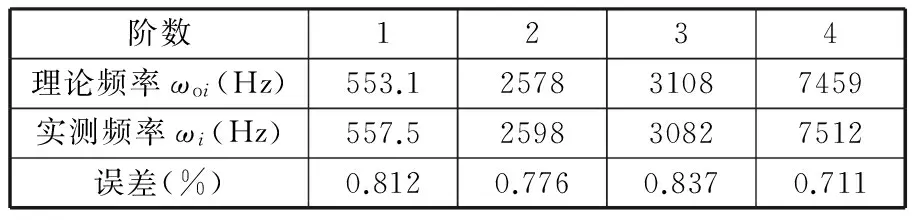
表2　理论及实测模态频率对比

通过对比表2中理论及实测模态频率可知，二者误差很小，说明约束子结构方法可以成功隔离整体结构对子结构的影响，构造出约束子结构的响应。

4.2约束子结构模型修正

以某发射台骨架的一个焊接钢管为例，研究复杂结构中约束子结构模型的构造及修正，实验模型及传感器布置方案如图6所示。

图6　发射台骨架模型及传感器布置方案

有限元建模中，单元类型选用Beam189单元，材料理论弹性模量207 GPa，泊松比为0.27，密度为7800 kg/m3，结构为瑞利阻尼。

实际结构由于受材料成形或加工等因素影响，往往与理论模型存在一定的误差，本文通过改变有限元模型中单元的弹性模量实现对模型的修正，即调整修正因子。

按照前述方法构造约束子结构振动响应，并对模型进行理论及实验模态分析，得到的理论和实测模态频率如表3所示。

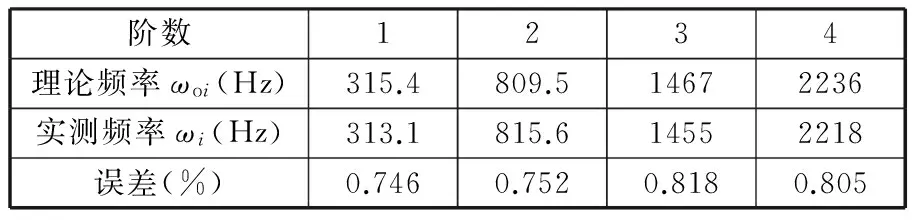
表3　理论及实测模态频率对比

将理论和实测模态参数代入式(24)，通过调整修正因子实现目标函数最小化，修正后理论模态频率与实测模态频率的对比如表4所示。

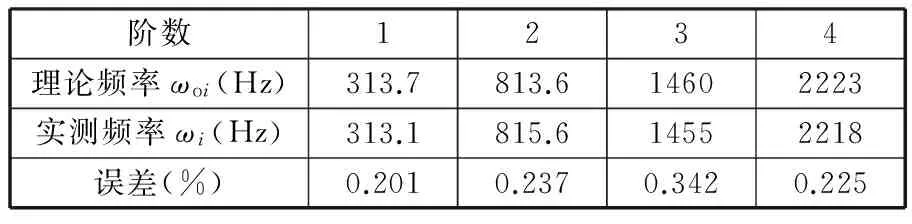
表4　修正后理论及实测模态频率对比

从表4可以看出，修正后的理论模型与实际结构间的误差进一步缩小，模型精度进一步提高，该理论模型可用于后续损伤识别研究。模型修正后各单元的修正因子如表5所示。

表5　优化后的修正因子

5　结论

(1)利用整体结构中子结构部分振动测试响应可直接构造约束子结构部分的响应，构造出的约束子结构模型能有效隔离整体结构对子结构的影响。

(2)利用构造的约束子结构振动响应对子结构部分进行模型修正，可以只建立子结构部分的模型，无需建立整体模型，方法简单、快捷，修正精度较高，所建立的约束子结构模型可用于后续损伤识别研究。

(3)由于只需建立子结构部分模型，因此待修正参数大大减少，在提高修正效率的同时，还可以得到较理想的修正结果。

[1]Imregun M，Visser W J．A Review of Model Updating Techniques[J].The Shock and Vibration Digest，1991，23(1)： 9-20．

[2]Mottershead J E，Friswell M I．Model Updating in Structural Dynamics[J].Journal of Sound and Vibration，1993，167(2)：347-375．

[3]Friswell M I，Mottershead J E．Finite Element Model Updating in Structural Dynamics[M].Netherlands：Kluwer Academic Publishers，1995．

[4]Fritzen C P，Jennewein D，Kiefer T．Damage Detection Based on Model Updating Methods[J].Mechanical Systems and Signal Processing，1998，12(1)：163-186．

[5]Perer R，Ruiz A．A Multistage FE Updating Proeedure for Damage Identification in Large-scale Structures Based on Multiobjeetive Evolutionary Optimization[J].Mechanical Systems and Signal Processing，2008，22(4)：970-991．

[6]张纯，宋固全．去噪正则化模型修正方法在桥梁损伤识别中的应用[J]．振动工程学报，2012，25(1)：97-102．

Zhang Chun，Song Guquan．Bridge Damage Identification by Finite Element Model Updatingwith Tikhonov Regularization and Wavelet Denoising[J]．Journal of Vibration Engineering，2012，25(1)：97-102．

[7]钟儒勉，宗周红，秦中远,等．基于多尺度模型修正的结合梁斜拉桥损伤识别方法[J].东南大学学报(自然科学版)，2014，44(2)：350-356．

Zhong Rumian，Zong Zhouhong，Qin Zhongyuan，et al．Damage Identification Method of Composite Cable-stayed Bridge Based on Multi-scale Model Updating[J]．Journal of Southeast University(Natural Science Edition)，2014，44(2)：350-356．

[8]李世龙，王天辉，马立元,等．大型复杂结构损伤识别两步法研究[J].中国机械工程，2012，23(9)：1051-1055．

Li Shilong，Wang Tianhui，Ma Liyuan，et al．Study on Two-step Damage Detection Methods of Large and Complex Structures[J]．China Mechanical Engineering,2012，23(9)：1051-1055.

[9]侯吉林，欧进萍．基于局部模态的约束子结构法[J].力学学报，2009， 41(5)：748-756．

Hou Jilin，Ou Jinping．Isolated Substructure Model Updating Method Based on Local Impulse Response[J]．Engineering Mechanics，2009，41(5)：748-756．

(编辑王艳丽)

Isolated Substructure Model Updating Method Based on Local Vibration Test Response

Guo JunlongMa LiyuanLi HuiLi Shilong

Ordnance Engineering College,Shijiazhuang,050003

A new method of isolation substructure was proposed to update a local substructure based on local vibration test responses, aiming to solve the problems of the excessive identification parameters and low efficiency applied in large complex structure model updating. The method utilized the local structure’s vibration test responses to construct the isolation substructure, in order to separate the substructure from the whole and constituted a simply independent structure, which could weaken the influence of the whole effectively. Then, the objective substructure was updated based on the responses of isolation substructure. Finally, a T shaped weld steel tube and the launch platform model were given to prove the effectiveness of the method. The results show that the proposed method contains fewer elements and can be updated easier with high efficiency, and it is well suitable for model updating of such large complex structure.

vibration test response; isolated substructure; model updating; objective function

2014-12-26

TU311DOI：10.3969/j.issn.1004-132X.2015.15.011

郭俊龙，男，1990年生。军械工程学院导弹工程系硕士研究生。主要研究方向为装备状态监测与故障预测。马立元，男，1962年生。军械工程学院导弹工程系教授、博士研究生导师。李辉，男，1972年生。军械工程学院导弹工程系副教授。李世龙，男，1987年生。军械工程学院导弹工程系博士研究生。