2D电液比例换向阀阀芯卡紧力分析

刘国文　阮　健　李　胜　孟　彬　左希庆

1.浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州，3100142.湖州职业技术学院，湖州，313000

2D电液比例换向阀阀芯卡紧力分析

刘国文1,2阮健1李胜1孟彬1左希庆1,2

1.浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州，3100142.湖州职业技术学院，湖州，313000

针对2D电液比例换向阀阀芯卡滞现象，应用缝隙流动原理，对2D阀芯有无偏心情况下的径向卡紧力进行系统理论分析，得到2D阀芯液压卡紧力计算方法；运用MATLAB软件进行数值计算，得出2D阀芯径向卡紧力与偏心量和高低压孔夹角间的关系；根据2D阀特性，提出2D电液比例换向阀阀芯改进措施，应用Fluent 软件对阀芯表面的流场进行CFD仿真分析，比较了改进前后的流速矢量和压力分布情况，验证了改进措施的正确性。改进后的2D电液比例换向阀在中高压实验中无“卡滞”现象出现，实现了高压大流量的比例控制。

2D；电液比例换向阀； 卡滞； 径向力；缝隙流动

0　引言

现有的电液比例换向阀一般采用直动式结构和导控式结构两种设计方案[1]。直动式比例换向阀或流量阀一般采用滑阀结构，因此容易受到摩擦力及油液污染的影响出现卡滞现象[2]。导控型电液比例阀一般采用直动式比例换向阀作为导阀，要获得较好的比例控制特性，导阀阀芯与阀芯孔之间必须具有较好的配合精度，否则容易出现卡滞现象，并在主阀上放大，对整个比例阀的特性产生较严重的不利影响。2D电液比例换向阀集直动、导控于一体，它通过压扭联轴器将2D换向阀与比例电磁铁相结合，使其兼具直动式和导控式电液比例换向阀的优点，实现高压大流量的比例控制。与传统滑阀一样，2D电液比例换向阀也存在液压卡紧的现象，主要表现为：中高压(如15 MPa以上时)情况下，阀芯卡紧力加大，导致流量无法上升。究其原因，其实质都是由于油液的压力引起阀芯所受的径向力不平衡导致的[3]。

不同于传统滑阀的是，2D电液比例换向阀可灵活利用其旋转自由度在具体结构设计上消除径向不平衡力，且2D电液比例换向阀特有的双自由度换向从根本上避免了由液压油污染造成的液压卡紧现象。经过合理设计，可以降低甚至杜绝卡紧故障的发生。因此本文对2D电液比例换向阀阀芯卡紧现象及其径向力作系统分析，有助于2D电液比例换向阀的优化设计及性能提高，及2D阀设计理论体系完善。

1　传统阀芯卡滞分析

滑阀副几何形状误差和同轴度变化所引起的径向不平衡液压力(即卡紧力)是传统阀芯产生液压卡紧现象的主要原因。当阀芯有一定锥度(锥部大端面向高压腔)时，此时轴心线平行但有偏心，从而产生径向不平衡力，该力使得阀芯与阀孔间的偏心距变大，当两者表面接触时，径向不平衡力最大。当阀芯表面有凸起且在阀芯高压端时，阀芯与阀孔的中心线不再平行，此时径向不平衡力最大，该力将阀芯的高压端凸起部分推向孔壁[3]。

当阀芯所受的径向力变大并超过一定程度时，阀芯与阀孔之间的油膜被破坏，阀芯与阀孔间的摩擦变成半干摩擦乃至干摩擦，能够将阀芯直接卡死。

2　2D阀阀芯卡滞分析

2.12D阀阀芯结构及原理

2D电液比例换向阀阀芯结构如图1所示，其两端台肩上按一定角度分布一对高低压孔(b、c和d、e)，两个高压孔P口通过阀芯内部通道相连，低压孔通过T口相通；阀芯两端的高低压孔与阀体上的直槽感受通道相交，形成两个微小的开口面积，串联构成液压阻力半桥，感受通道与两端敏感腔相通，从而控制敏感腔的压力变化[4]。当阀芯旋转时，高低压孔与感受通道相交的面积发生变化，导致两端敏感腔压力发生变化，压力差使阀芯轴向失去平衡产生向左或向右的移动[4]。

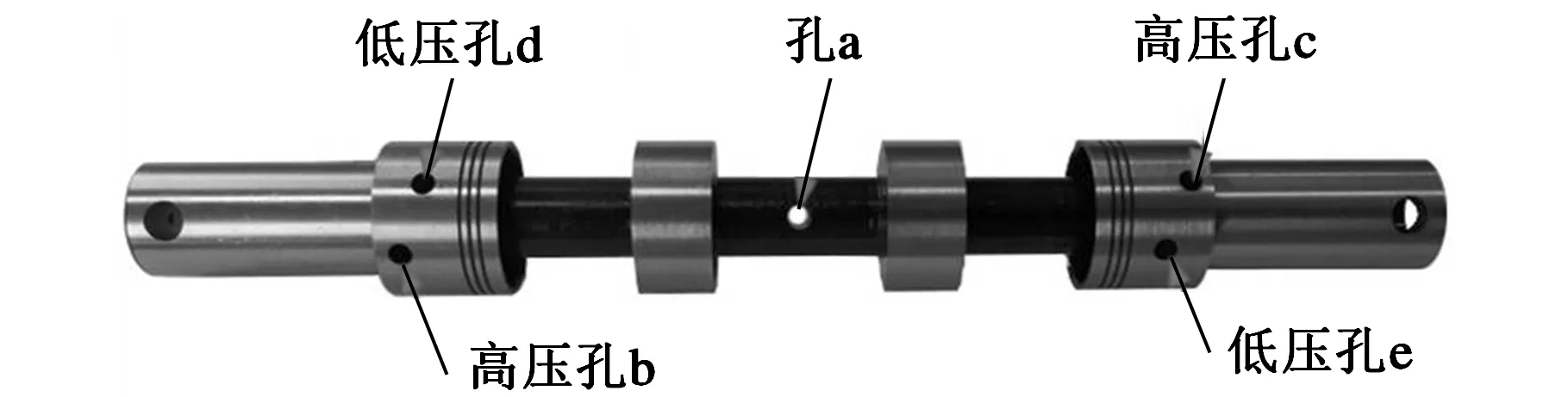
图1　阀芯结构

2.22D阀阀芯缝隙流动分析

由2D阀阀芯结构可知，图2中阀芯台肩上高压孔向低压孔的泄漏流动可近似认为是倾斜壁面缝隙间的流动，其间隙高度是转角的函数[5]。由于缝隙是微小量，故其泄漏量为

(1)

(2)

式中，Q为泄漏量,L/min; b为间隙宽度,mm;hθ为间隙高度，mm;μ为油液动力黏度，Pa·s; r0为阀芯半径，mm;dF为微小卡紧力，N;dθ为微小转角，(°)；C为流量系数，取为0.62。

理想状态下，2D阀阀芯无偏心，间隙高度hθ为定值，由式(2)可知图2中上侧压力与下侧压力相等，该力在同一方向上合力大小相等，方向相反，因此只会产生微小阻力矩，不会导致卡紧现象产生，其受力分布如图3所示。

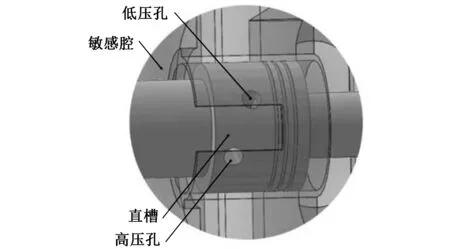
图2　感受通道与高低压孔位置关系

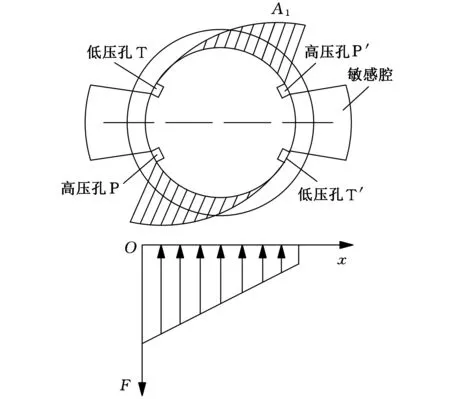
图3　无偏心时压力分布

2D阀阀芯发生旋转或由其他原因引起偏心时，间隙hθ随转角θ发生变化，导致上下侧压力分布发生变化，如图4所示，由于油液始终从高压孔向低压孔泄漏，上侧缝隙流动为从P′到T，下侧流动为从P到T′, 可判定P′到T为渐扩缝隙流动，P到T′为渐缩缝隙流动。

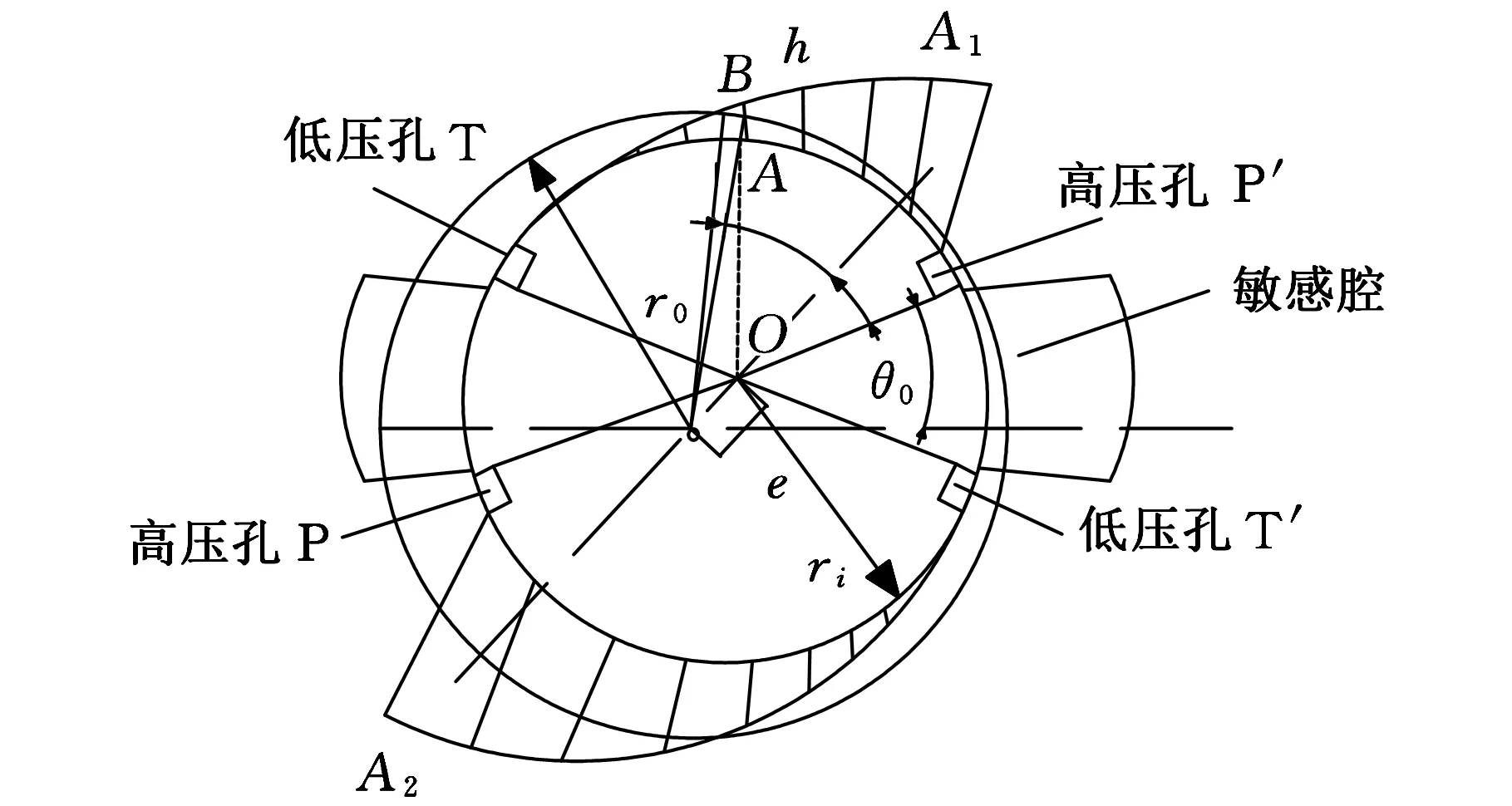
图4　有偏心时压力分布

对于渐扩缝隙流动，由伯努利方程可知，其流速会增大，因而其压力会减小。由图4可得

hθ1=lAB=lOB-lOA=

r0-(ri+ecosθ)=δ-ecosθ

(3)

δ=r0-ri

式中，lAB为A、B两点的距离；lOB为O、B两点的距离；lOA为O、A两点的距离；ri为偏心时圆心与壁面的距离变量；e为偏心距。

对于渐缩缝隙流动，同样由伯努利方程可知，其流速会减小，因此其压力会增大，可得

hθ2=lAB=lOB-lOA=

r0-(ri-ecosθ)=δ+ecosθ

(4)

由于δ和e同为微小量，为计算方便，可近似认为

δ≈e

(5)

由式(2)和式(3)得到渐扩缝隙流动中F对θ的微分式为

(6)

由式(2)和式(4)得到渐缩缝隙流动中F对θ的微分式为

(7)

令

对式(6)积分得

(8)

θ∈(-θ0,π-θ0-2φ)

式中，θ0为阀芯偏心量；φ为高低压孔半夹角；FA1为对上壁面积分得到的压力。

对式(7)积分得

(9)

θ∈(π-θ0,2π-θ0-2φ)

式中，FA2为对下壁面积分得到的压力。

FA1和FA2在水平方向和垂直方向上的分量分别为

(10)

由此可得，2D阀芯水平和垂直方向的卡紧力分别为

FX=FA2cosθ-FA1cosθ

(11)

FY=FA2sinθ-FA1sinθ

(12)

由此可得2D阀芯径向卡紧合力为

(13)

FA2∈(-θ0,π-θ0-2φ)

FA1∈(2π-θ0-2φ,π-θ0)

2.32D阀芯卡紧力数值计算

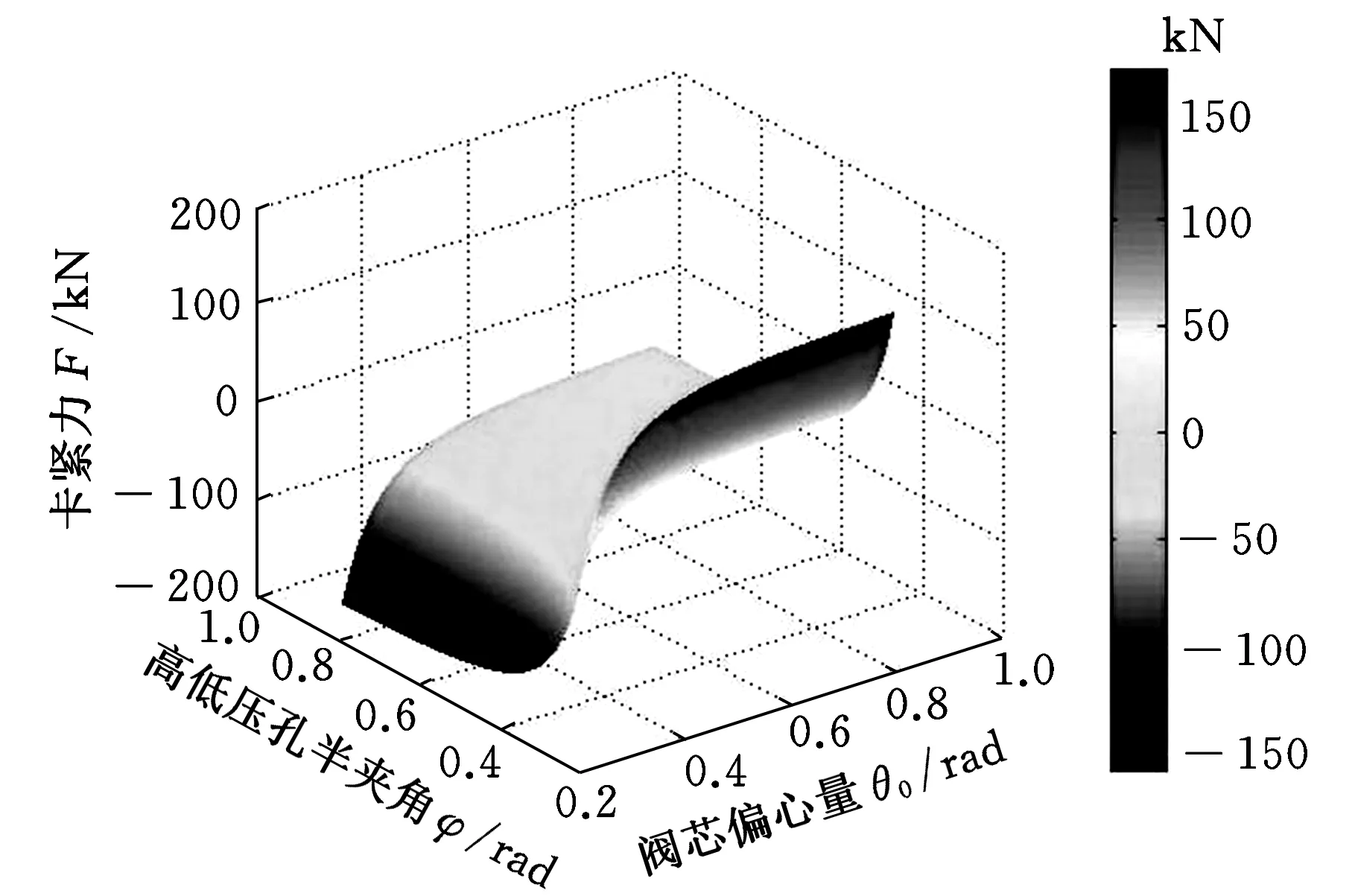
图5　F、θ0和φ关系

由于卡紧力F为零时式(10)为隐函数，无法精确计算出θ0和φ的数值，从图6可看出卡紧力F趋近于零时，θ0和φ相差不大。

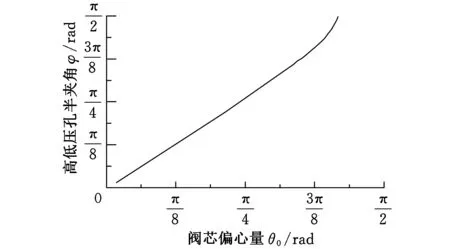
图6　F=0时θ0与φ关系曲线

2D阀设计中，高低压孔半夹角φ取决于敏感通道的宽度。φ过小时，敏感腔的压力变化不大，会导致响应速度变小；φ过大时，其卡紧力会随之升高，且阀的体积会变大，因此高低压孔半夹角φ一般取值范围为[π/16,π/8]。 当φ值固定时，卡紧力F随θ0的变大而增大，当θ0≈π/8时，F趋近最大值，增长趋缓，如图7所示。

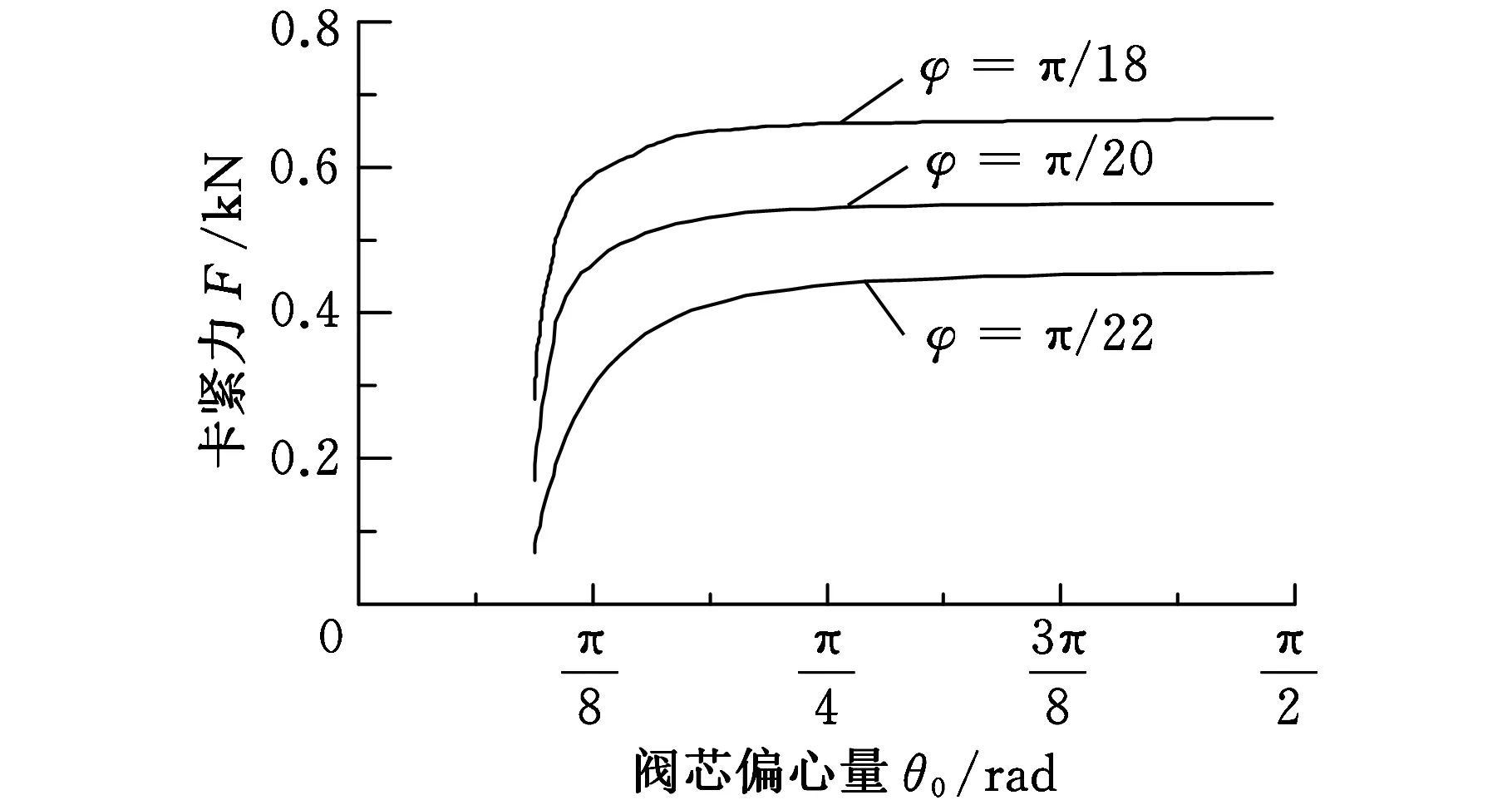
图7　φ取定值时F与θ0的关系曲线

3　改进措施

为了最大限度地减小阀芯液压卡紧力，滑阀阀芯一般采用以下措施[7-8]：①提高阀的加工和装配精度，避免偏心产生，但该措施受限于加工成本；②在阀芯台肩上，加工几道一定尺寸的均压槽，可起到平衡径向力的作用；③通过控制器对电磁铁加高频小振幅的颤振信号，使阀芯沿轴向或圆周方向产生高频小振幅的振动或摆动；④提高油液清洁度。考虑到2D电液比例换向阀自身结构的特点，2D阀芯除采用上述措施外，还可采取特有的改进措施：在每个高低压孔口上方均加工一弓形平面沉槽，如图8所示，高低压孔加工于弓形槽平面上，阀芯与阀体装配后，弓形高低压孔沿阀芯周向的切边与直槽感受通道的切边平行。这种方法不但增大了阀的导控面积梯度和导控流量，从而缩短阀的响应时间，而且还增大了高低压孔之间的空间，使高压孔到低压孔之间的缝隙流动更为均匀，大大减小了由于高低压孔之间缝隙流动所导致的径向不平衡力[9-11]。

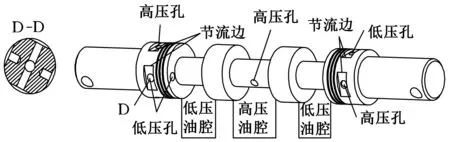
图8　弓形高低压孔阀芯

上述改进措施会导致高低压孔之间的泄漏量有所增大，经计算可知：只要保持高低压孔之间距离适当，可控制该泄漏量至最小，其降低2D阀芯卡紧力的效果应较为明显。

4　仿真分析

应用Fluent软件对阀芯表面的流场进行CFD仿真分析，仿真参数如表1所示。分析了阀芯改进前后阀芯和阀芯孔壁面之间液流的速度分布和压力分布，可直观发现2D阀在消除液压卡紧力方面有独特的优势，合理设计，可降低甚至根除液压卡紧力[12]。

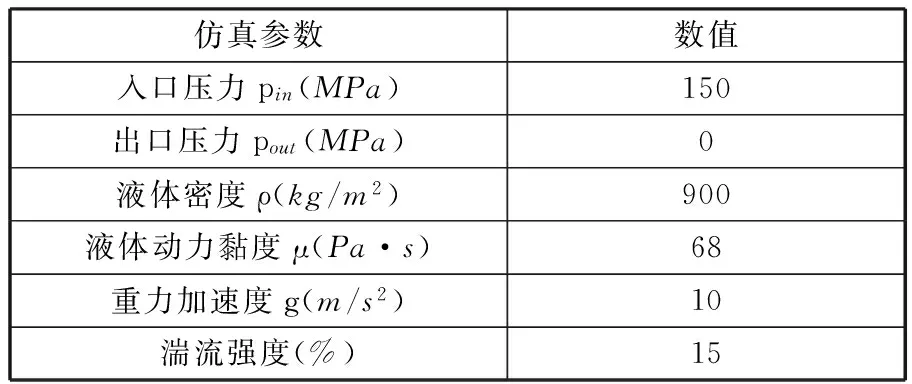
表1　仿真参数

4.1流场流速分析

图9所示为阀芯改进前后上下壁面液流的速度分布情况。仿真结果表明：阀芯改进前，上下壁面的速度场中液流速度都比较快，导致局部压力过高，从而压迫上下壁面反作用于阀芯，产生偏心力，且该偏心力随液流变化而变化，呈无序状态；而改进后液流所经过的容腔体积变大，速度分布明显趋缓，偏心力变小，阀芯卡紧力得到控制。

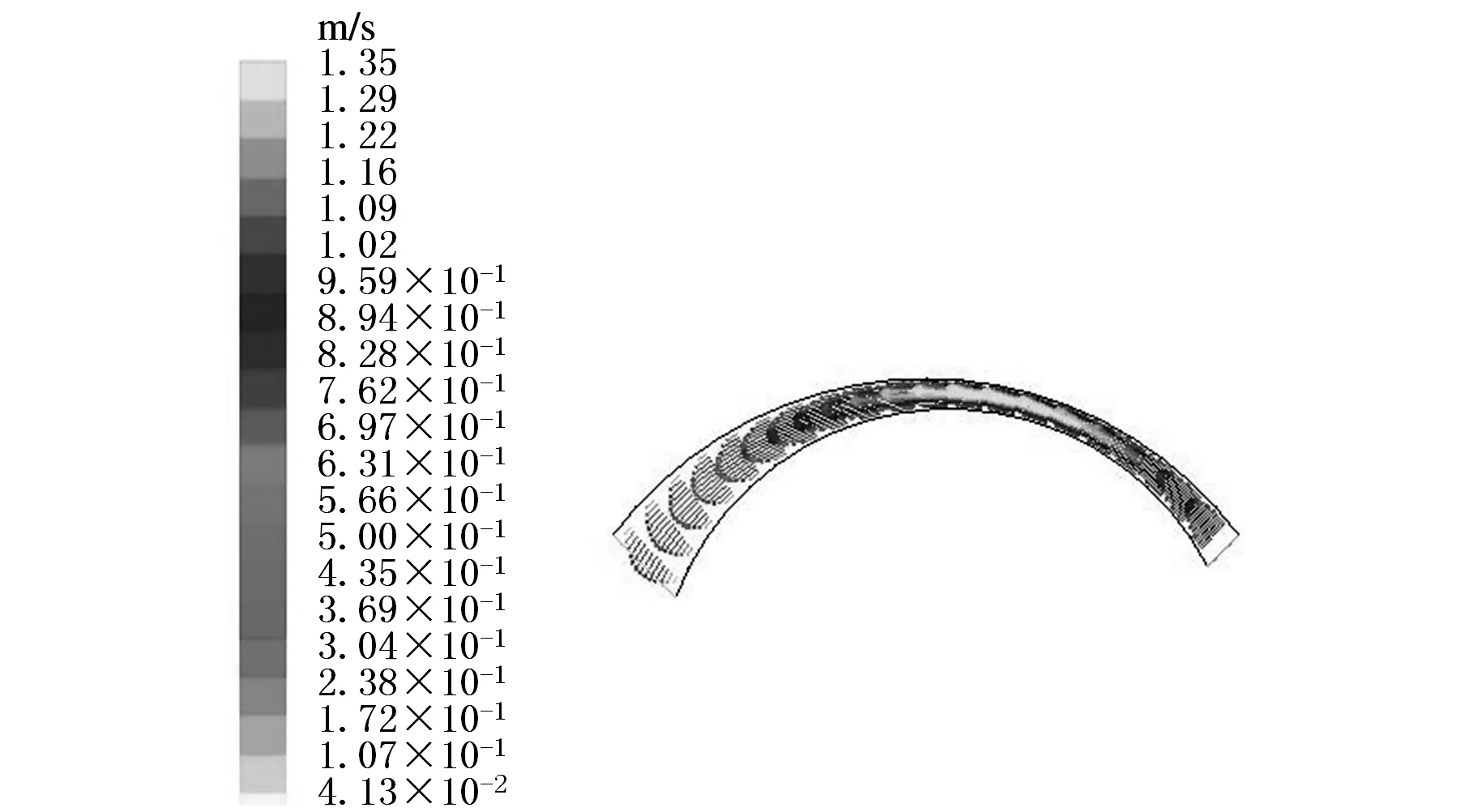
(a)上壁改进前

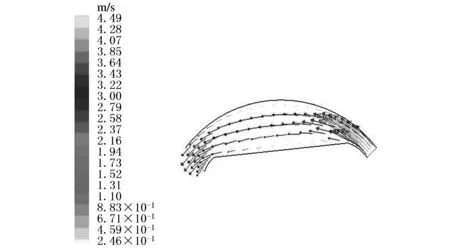
(b)上壁改进后

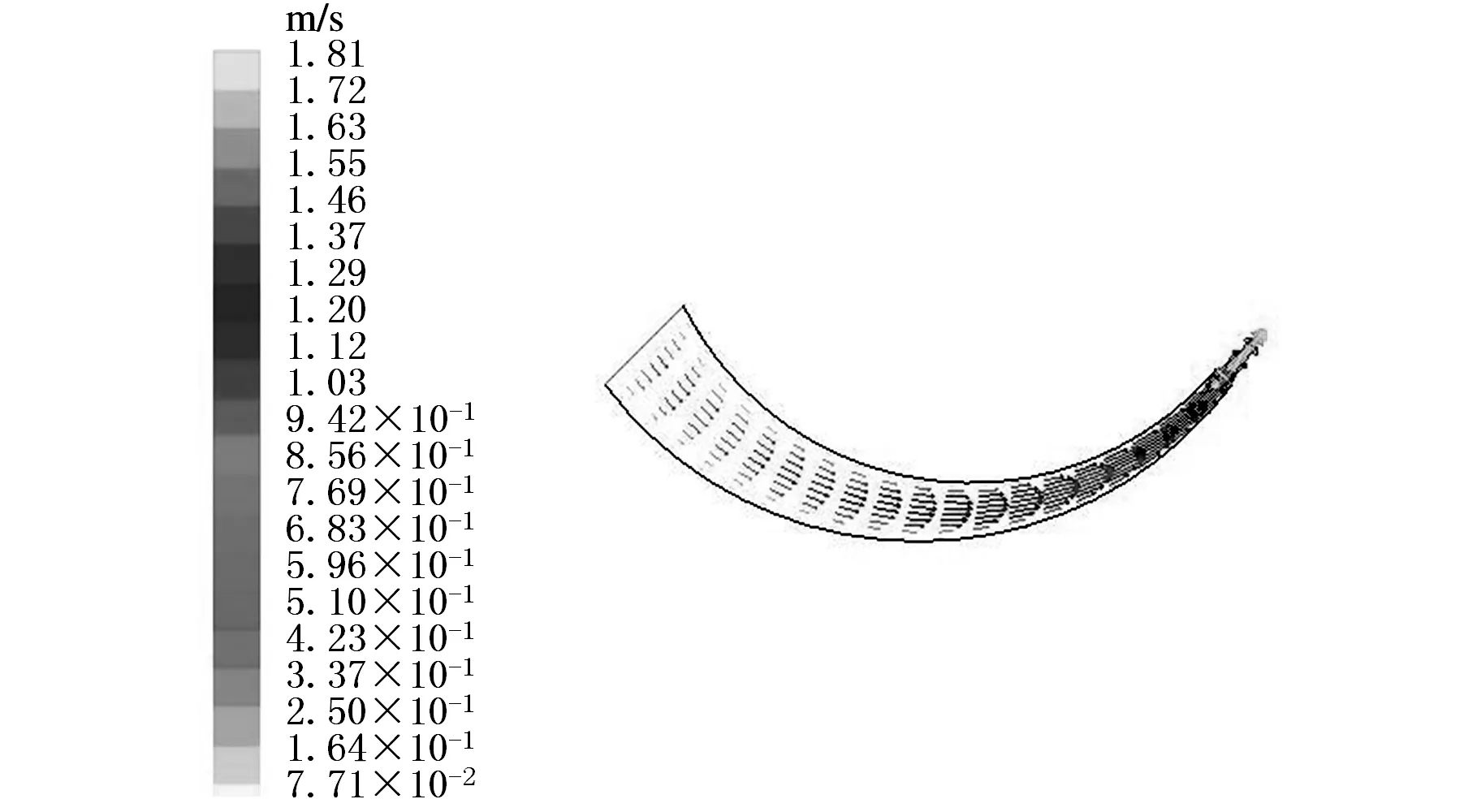
(c)下壁改进前

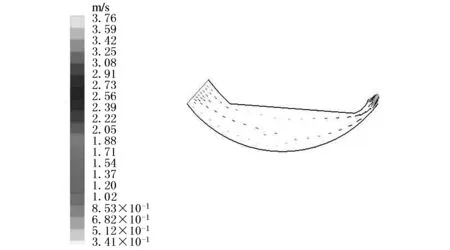
(d)下壁改进后图9　速度分布

4.2压力分布分析

图10和图11为阀芯改进前后上下壁面压力的分布曲线。对其对称壁面所受压力分布进行对比可以看出， 阀芯改进前，压力分布比较集中，较易出现压力极值，这是形成机械卡紧的主要原因；改进后其对称壁面的压力分布曲线面积大致相等，表明压力分布趋于平衡，有效地减小了阀芯卡紧力。

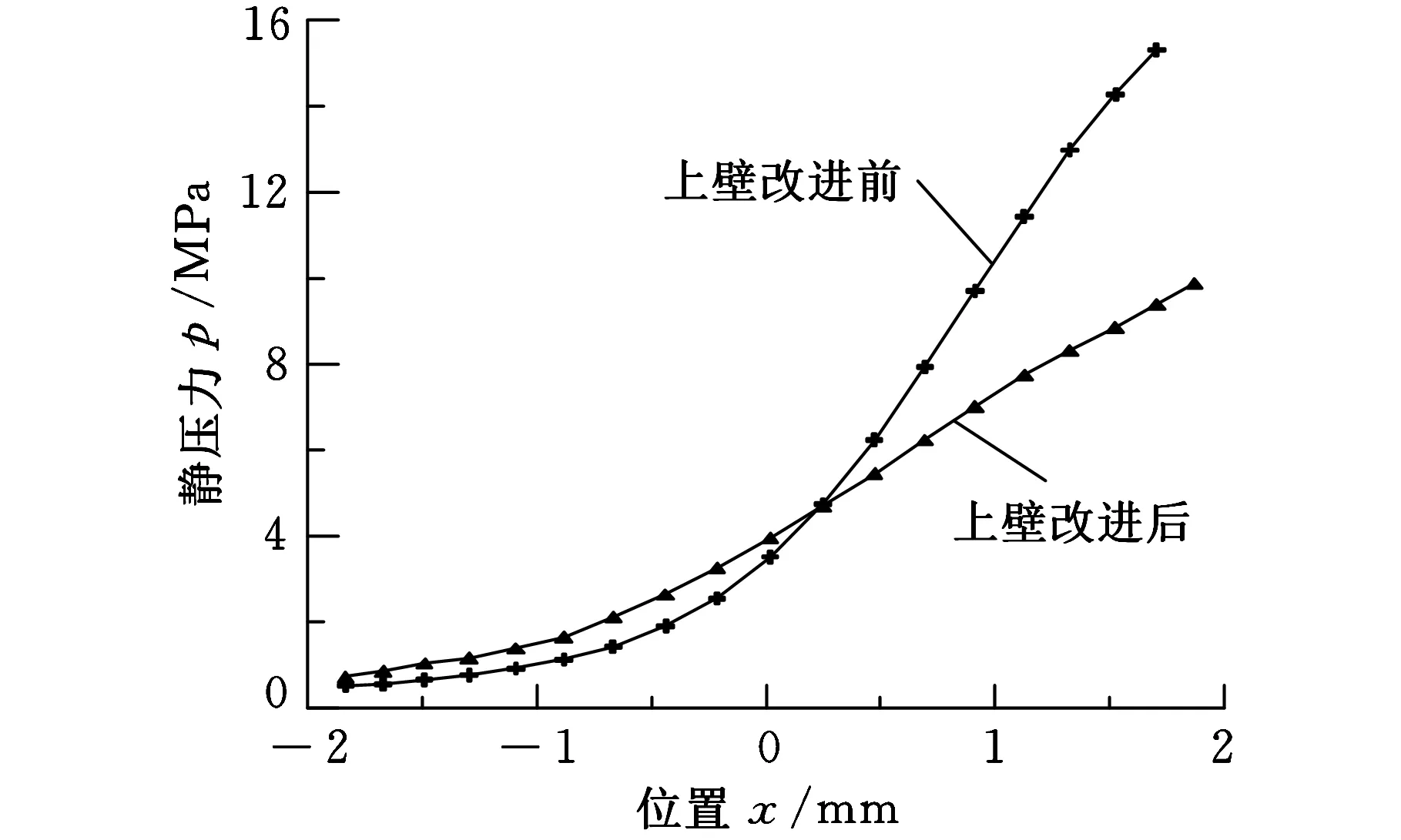
图10　上壁压力改进前后曲线

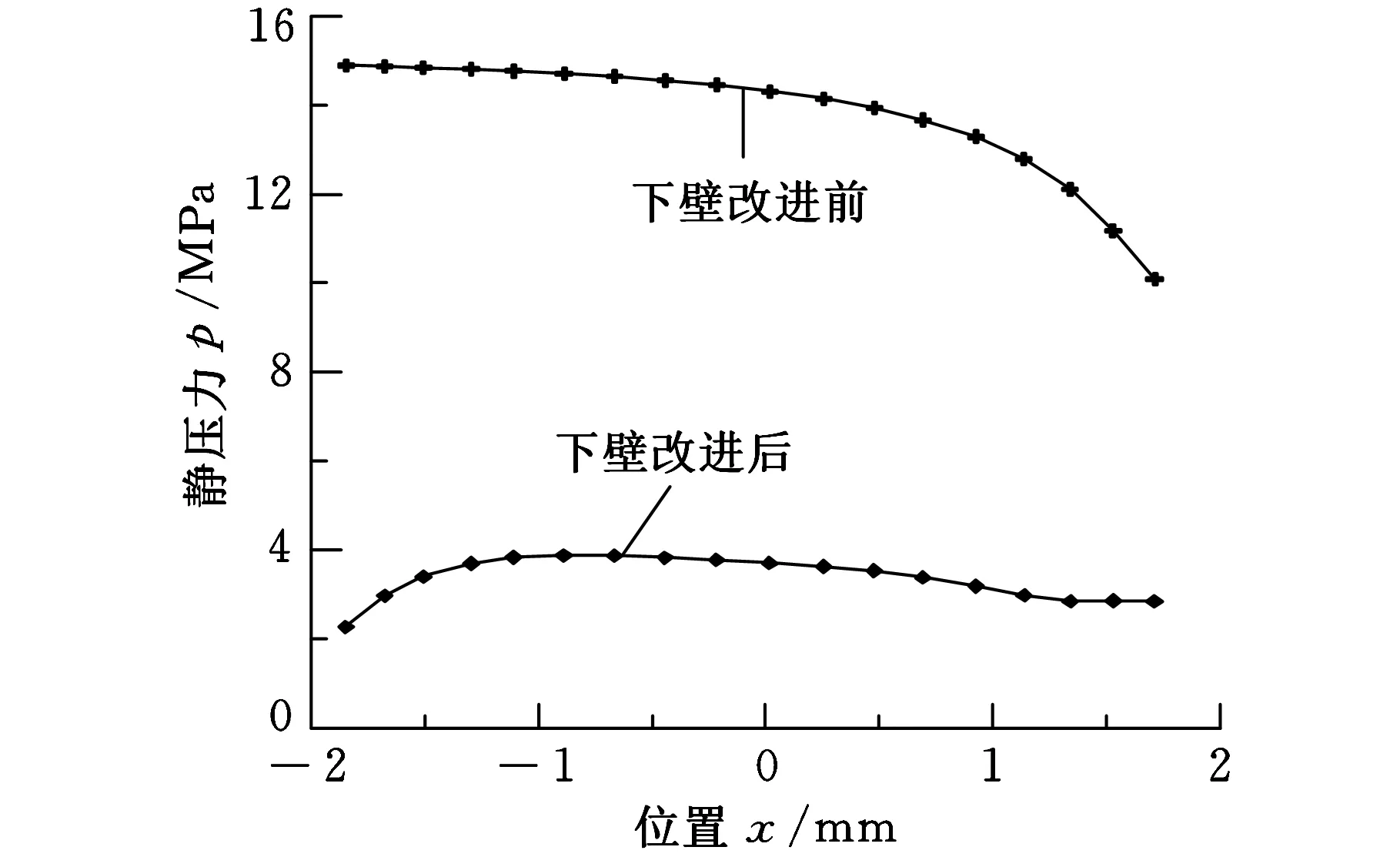
图11　下壁压力改进前后曲线

5　结论

(1)应用缝隙流动原理和MATLAB软件分析，得到2D阀芯径向卡紧力与偏心量和高低压孔夹角间的关系，2D阀芯卡紧力F随着偏心量θ0或高低压孔夹角φ的增大而变大。

(2)2D电液比例换向阀阀芯径向不平衡力与2D阀自身结构有关联，通过合理设计高低压孔的分布方式和阀芯旋转角度，可降低甚至根除液压卡滞故障。

(3)提出降低2D阀阀芯卡紧力的改进方案，运用Fluent软件分析了阀芯改进前后液压卡紧力的分布情况，验证了该方案的正确性。

(4)改进后的2D电液比例换向阀在中高压实验中无卡滞现象出现，实现了高压大流量的比例控制。

[1]黎啟柏. 电液比例控制与数字控制系统[M]. 北京：机械工业出版社, 1997.

[2]李伟,李伟波,吴根茂,等. 滑阀机构液压卡紧无传感器诊断方法研究[J].中国机械工程,1999, 10(4)：1093-1096.

LiWei,LiWeibo,WuGenmao,etal.TheResearchofSensorlessDiagnosticApproachforSpoolClamping[J].ChinaMechanicalEngineering，1999, 10(4)：1093-1096.

[3]王积伟. 液压传动[M]. 北京：机械工业出版社, 2007.[4]RuanJ，BurtonR，UkrainetzP.AnInvestigationIntotheCharacteristicsofaTwoDimensional“2D”FlowControlValve[J].JournalofDynamicSystems,Measurement, 2002，124:214-220.[5]盛敬超. 液压流体力学[M]. 北京：机械工业出版社, 1980.

[6]薛定宇,陈阳泉. 高等数学应用问题的Matlab求解[M]. 北京：清华大学出版社,2004.

[7]裴翔，李胜，阮健. 转阀阀芯卡紧现象的分析及减小措施[J]. 机床与液压，2000(5):74-78.

PeiXiang,LiSheng,RuanJian.TheAnalysisandImprovementofSpoolClampingforRotaryValve[J].MachineTool&Hydraulics, 2000(5):74-78.

[8]姜燕，王文汉，贾占良. 高精度液压滑阀卡紧问题分析与改善[J]. 机床与液压，2011(9):112-114.

JiangYan,WangWenhan,JiaZhanliang.TheAnalysisandImprovementofHighPrecisionSpoolClamping[J].MachineTool&Hydraulics, 2011(9):112-114.

[9]李胜. 2D伺服阀数字控制的关键技术的研究[D]. 杭州：浙江工业大学, 2011.

[10]LiSheng，RuanJian,BurtonR,etal. 2DSimplifiedServoValve[J].ChineseJournalofMechanicalEngineering,2003,16(2):132-135.

[11]阮健. 电液(气)直接数字控制技术[M]. 杭州：浙江大学出版社，2000.

[12]韩红彪,高善群,李济顺. 圆盘转子流体阻力分析与试验研究[J].中国机械工程, 2013, 24(15)：2093-2096.

HanHongbiao,GaoShanqun,LiJishun.FluidResistanceAnalysesandExperimentalResearchofDiscRotor[J].ChinaMechanicalEngineering，2013，24(15)：2093-2096.

(编辑王艳丽)

Analysis of Spool Cliping Force for 2D Electro-hydraulic Proportional Directional Valve

Liu Guowen1,2Ruan Jian1Li Sheng1Meng Bin1Zuo Xiqing1,2

1.Key Laboratory of Special Purpose Equipment and Advanced Processing Technology,Ministry of Education，Zhejiang University of Technology,Hangzhou,310014 2.Huzhou Vocational & Technical College,Huzhou,Zhejiang,313000

To solve clamping malfunction of the spool which was caused in the 2D electro-hydraulic proportional valve under high pressure situation, applicating the theory of gap flow, the radial force of 2D valve under eccentric and non-eccentric situations was systematically analyzed and a computational formula of 2D valve clamping force was deduced.Using software MATLAB the analysis result was calculated to get the relationship between 2D valve clamping force and the eccentricity with the angle between the high pressure and low pressure holes. Based on the 2D valve’s property, the improvement measures of solving spool clamping malfunction were put forward, The flow field of the spool surface was CFD simulated and analysed by using Fluent software. Based on the velocity vector and pressure distribution of the spool, the improvement measure of solving spool clamping malfunction is proved correct. The design philosophy of 2D electro-hydraulic proportional valve is improved, high pressure and large flow proportional control is achieved in improved 2D electro-hydraulic proportional valve.

2D；electro-hydraulic proportional valve；clamping；radial force；gap flow

2014-10-11

国家自然科学基金资助项目(51375445)；国际科技合作专项资助项目(2011DFA72690)；浙江省自然科学基金资助项目(LZ13E050002)；湖州市科技局基金资助项目(2013YZ10)

TH137DOI：10.3969/j.issn.1004-132X.2015.15.002

刘国文，男，1976年生。浙江工业大学机械工程学院博士研究生，湖州职业技术学院机电与汽车工程学院讲师。主要研究方向为流体控制元件及电液数字控制研究。发表论文10余篇。阮健，男，1963年生。浙江工业大学机械工程学院教授、博士研究生导师。李胜，男，1968年生。浙江工业大学机械工程学院教授、博士。孟彬，男，1979年生。浙江工业大学机械工程学院讲师、博士。左希庆，男，1975年生。浙江工业大学机械工程学院博士研究生，湖州职业技术学院机电与汽车工程学院副教授。