基于子结构的Woodbury非线性分析方法

苏 璞，李 钢，余丁浩

(大连理工大学海岸和近海工程国家重点实验室，辽宁，大连 116024)

随着工程结构规模和复杂程度的日益增加，非线性分析已经成为研究结构损伤演化规律的重要手段。材料非线性是土木工程领域常见的一种非线性行为，准确模拟结构材料非线性行为对结构性能评估意义重大。

对于材料非线性问题，数值求解过程需重复合成和分解整体刚度矩阵，尤其是自由度规模比较大时，计算成本大幅增加，耗费时间通常难以接受，尽管计算机性能的不断提高在一定程度上缓解了这一问题，但高效的非线性数值算法依然是众多学者追求的目标，许多分析方法不断涌现，如多尺度方法[1－3]，子结构方法[4－6]等。其中，子结构概念最初用于求解线弹性问题[7]，Clough等[8]将其进一步扩展到非线性问题中，其核心思想是将整体结构划分为线弹性子结构和非线性子结构，通过静力凝聚的方式消去弹性子结构的内部自由度，大幅降低了系统自由度数目，提高了计算效率，之后该方法被众多学者进一步完善，并应用于不同结构的非线性分析[9－12]，但该方法需要提前预测非线性发生的区域，其发展受到一定限制，为克服其局限性，Han和Abel[13]提出了自适应子结构方法，该方法可根据结构非线性状态动态的划分弹性和非线性子结构，无需预判非线性发生的区域；Sheu等[14－15]基于多级剖分策略提出了可考虑非线性区域变化的子结构分析方法。此外，有学者基于混合变分原理提出了双重子结构方法[16－17]，该方法以界面力为未知量，其界面方程规模一般小于或等于传统的子结构方法[18]。尽管子结构方法降低了结构整体刚度矩阵的阶数，但在材料非线性分析过程中仍不可避免的需要对子结构刚度矩阵进行分解运算，该过程通常耗时较多，仍会在一定程度上降低整体效率。

对于大多数工程结构，材料非线性行为一般仅发生在局部区域，即结构整体刚度矩阵只有少量元素发生变化，传统变刚度法须对整体刚度矩阵实时更新和分解，无法充分考虑结构的局部非线性特征。而在数学领域，对于仅有少量元素变化的矩阵，可通过Woodbury公式快速求逆，目前已有许多学者将该公式应用于局部非线性问题[19－22]。Woodbury公式的使用避免了整体刚度矩阵的实时更新和分解，仅需对小规模的Schur补矩阵进行分解，进而有效提升计算效率。为了将Woodbury公式应用于一般有限元问题，李钢等[23]基于材料应变分解的思想提出了隔离非线性有限元法，在该方法中，结构的非线性特征由额外设置的非线性自由度来体现，而整体刚度矩阵始终保持不变，当结构非线性规模较小时，结构非线性自由度数也较少，结合Woodbury公式仅需对与非线性自由度相关的小规模的Schur补矩阵进行分解，从而实现非线性问题的高效求解[24]。然而，Schur补矩阵通常为满阵，当结构非线性规模比较大时，Schur补矩阵阶数也随之增大，对其进行分解的计算成本大幅增加，导致Woodbury公式的高效性受到限制。

本文以子结构和隔离非线性有限元法为基础，提出基于子结构的Woodbury非线性分析方法；该方法将整体结构划分为若干个子结构的同时，也将Schur补矩阵分解为若干个子矩阵(即子结构的Schur补矩阵)，有效降低了Schur补矩阵的规模；且整个分析过程仅需对子结构的Schur补矩阵进行分解，改进了 Schur补矩阵阶数较大时 Woodbury公式计算效率降低的不足，进一步拓展了Woodbury公式的适用范围；依据时间复杂度理论建立效率分析模型，并通过数值算例证明了本文方法的准确性和高效性。

1 基本理论

1.1 子结构法

子结构法是将整体结构的求解域划分为若干个子域，各子域对应的部分被定义为子结构，子结构间相邻的部分称为界面；同时，整体结构位移自由度随之分为内部自由度和界面自由度，通过静力凝聚消去内部自由度，即可得到一个仅与界面自由度相关的控制方程。因此，子结构法是通过“化整为零”的方式缩减问题规模，其求解流程为：将整体结构划分为若干个子结构；装配子结构得到界面方程；利用界面信息得到每个子结构的响应[8]。

假定某结构求解域为Ω，边界为Γ，如图1(a)所示；依据子结构法将整体结构划分为若干个子结构，这里以两个子结构为例，如图1(b)所示；其中：子结构1和子结构2对应的求解域分别为Ω1和Ω2；Γ1和Γ2分别为Ω1和Ω2所独有的边界，而Γ12为Ω1和Ω2的公共界面。

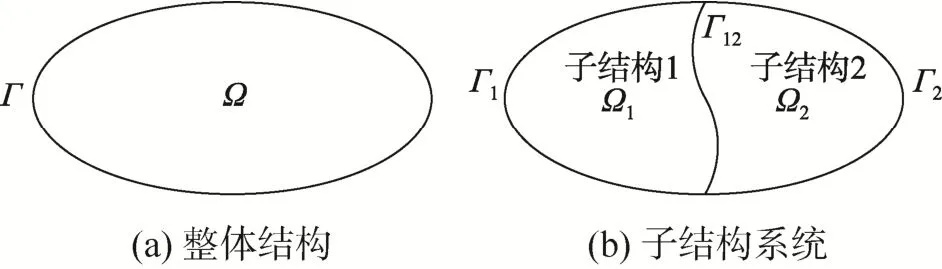
图1 子结构方法示意Fig.1 Diagram of substructuring method

这里将由子结构组成的系统定义为子结构系统[25]。考虑界面处子结构间的相互作用力以及位移连续性条件，则子结构系统的平衡方程和位移协调方程分别为[17]：

式中：s为子结构编号；NS为子结构个数，这里NS=2；K(s)、u(s)和F(s)分别为子结构s的刚度矩阵、位移向量和荷载向量；λ为拉格朗日乘子；B(s)是与位移自由度相关的矩阵。由式(1)解得u(s)，并将其代入式(2)，可得到子结构系统的界面方程为：

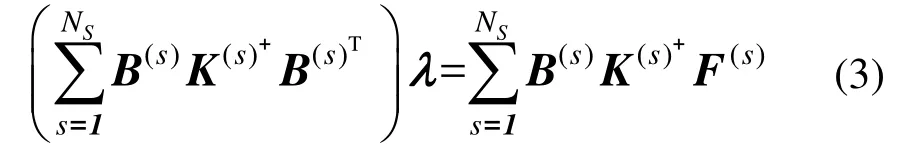
其中：为子结构s刚度矩阵K(s)的广义逆[16]，当K(s)非奇异时，。式(3)通常采用共轭梯度法来求解，将λ回代到式(1)，即可得到各子结构的位移响应。在整个求解过程中，仅需对各子结构刚度矩阵K(s)进行更新和分解，避免了对结构整体刚度矩阵的相应运算，可有效降低计算成本。

1.2 基于Woodbury公式的结构分析方法

Woodbury公式(详见附录)现已被广泛应用于高效求解结构非线性问题[19－22]，该类方法可统一称为基于 Woodbury公式的结构分析方法(以下简称Woodbury法)。隔离非线性有限元法作为一种高效的Woodbury法，其以有限元基本理论为基础，具有通用性好，适应范围广的特点。

隔离非线性有限元法的核心思想是将材料应变分解为线性和非线性两部分。以图2所示的单轴应力-应变关系作简要介绍，假设某个增量步内，材料非线性状态由A点到B点，应变增量Δε根据初始初始弹性模量Ee可分解为：

式中：Δεʹ为线弹性应变增量；Δεʺ为非线性应变增量。与应变增量Δε对应的应力增量Δσ可表示为：

当考虑多维材料本构关系时，上述应变分解过程同样适用，此时式(4)和式(5)可相应写为：

式中：Δε、Δεʹ和 Δεʺ分别为应变向量、线弹性应变向量和非线性应变向量；Δσ为应力向量；De为材料初始弹性本构矩阵。

图2 应变非线性分解Fig.2 Nonlinear decomposition of material strain

基于上述应变分解思想，结合虚功原理可得到隔离非线性有限元法的控制方程为[23]：

式中：Ke为结构的初始弹性刚度矩阵；Kr为系数矩阵，代表结构非线性自由度与节点力之间的关系；Krr为分块对角矩阵，体现结构材料非线性变形信息；Δu和分别为结构的结点位移向量和非线性应变向量；ΔF为结构结点荷载向量。采用Woodbury公式求解上述控制方程，可得：

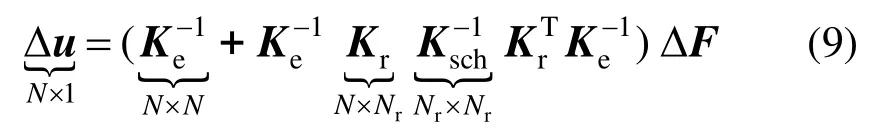
2 基于子结构的Woodbury法

2.1 控制方程

依据有限元法对图1(a)所示结构的求解域进行离散化，如图3(a)所示；采用子结构法将整体结构划分为若干个子结构，这里以NS=2为例，相应子结构系统如图3(b)所示。图3中深色部分表示结构在外荷载作用下可能发生非线性变形的区域。各子结构结点分为界面结点和内部结点，子结构s的结点位移自由度N(s)相应表示为：

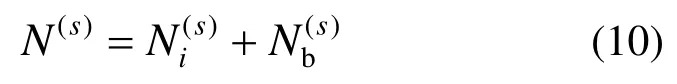
图3 子结构剖分示意Fig.3 Diagram of substructuring partition

将1.2节中应变分解思想应用于各子结构，并考虑子结构之间的变形协调关系，可得子结构系统的平衡方程和位移协调方程分别为：

式中：

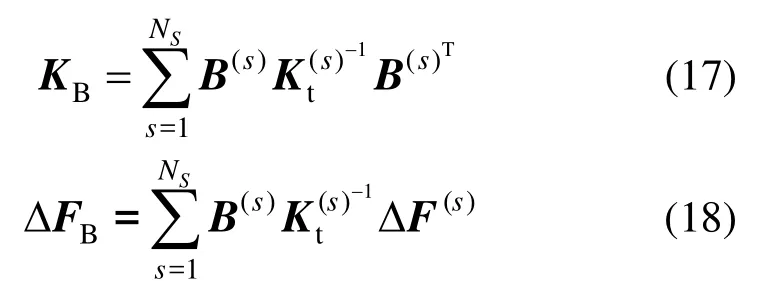
由式(3)、式(15)、式(16)、式(17)和式(18)可知，子结构法在求解界面方程时，需对子结构刚度矩阵K(s)进行更新的分解，而基于子结构的Woodbury法仅需对小规模的矩阵进行分解。

2.2 方程求解

本文控制方程的迭代求解方案基于 Newton-Raphson(简称N-R)格式，每一个N-R迭代步需依次求解式(16)和式(14)，其中式(16)采用共轭梯度法求解，具体迭代格式如图4所示。

由图4可知，在共轭梯度法求解Δλ的过程中，由于合成ΔFB和计算乘积KBpk涉及到子结构Schur补矩阵的分解或回代运算，计算量较大；其余基本是矩阵和向量或向量和向量的乘积运算，计算量相对较小，可忽略不计。

求解式(16)得到Δλ后，将其回代到式(14)即可得到各子结构的位移 Δu(s)。对比式(9)和式(14)可知，传统Woodbury法需分解整体结构的Schur补矩阵Ksch，而基于子结构的 Woodbury法仅需分解各子结构的 Schur补矩阵(s=1,2,…,NS)。图5给出了Ksch和的具体形式，由图5可知，的阶数与整体结构非线性自由度数相关，而的阶数仅与子结构s的非线性自由度数相关，因此，的阶数一般低于Ksch的阶数，且的阶数随子结构数的增多而降低。

图4 共轭梯度法迭代格式Fig.4 Iterative format of conjugate gradient method

图5 Schur补矩阵的阶数示意Fig.5 Dimension of Schur complement matrix

此外，通过对比式(14)、式(15)、式(17)和式(18)可知，回代求解位移 Δu(s)、计算乘积KBpk和合成ΔFB的计算过程相差不大。例如对于乘积KBpk，其计算过程从右到左依次执行，首先，计算向量pk与矩阵的乘积，即：

图6 qk 具体计算步骤Fig.6 Detailed calculation steps of qk

由此，便完成了乘积KBpk的计算(上述变量均为中间变量)。回代求解位移Δu(s)和合成ΔFB均可分解成上述类似的步骤进行运算。值得注意的是，由于计算ΔFB的过程中已经对矩阵进行了分解，因此后续在计算KBpk和回代求解位移 Δu(s)时，只需要对矩阵进行回代即可。

3 时间复杂度效率模型

时间复杂度作为一种仅与算法本身相关的效率评价方法，具体是指算法执行过程中所需的计算工作量，能相对客观地评价一个算法的效率[26－27]。

根据2.2节论述可知，基于子结构的Woodbury法在求解过程中，合成ΔFB、计算KBpk和回代求解位移 Δu(s)三项由于涉及到子结构 Schur补矩阵的分解或回代运算，计算量较大，其余运算计算成本相对较小，可忽略不计。此外，上述三项的计算过程也相似，以乘积KBpk为例，分别统计其计算过程每一步骤的时间复杂度并汇总，即可得到计算KBpk的时间复杂度，见表1。合成ΔFB和回代求解位移 Δu(s)的时间复杂度也可通过类似的方式得到，本文不再赘述。将上述三项的时间复杂度汇总并忽略低阶项，即可得到基于子结构的 Woodbury法的时间复杂度，见表2。

表1 计算KBpk的时间复杂度Table 1 Time complexity of calculating KBpk

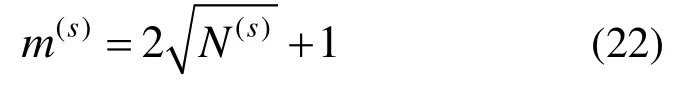
结合式(22)，则基于子结构的Woodbury法的时间复杂度TPro可表示为：

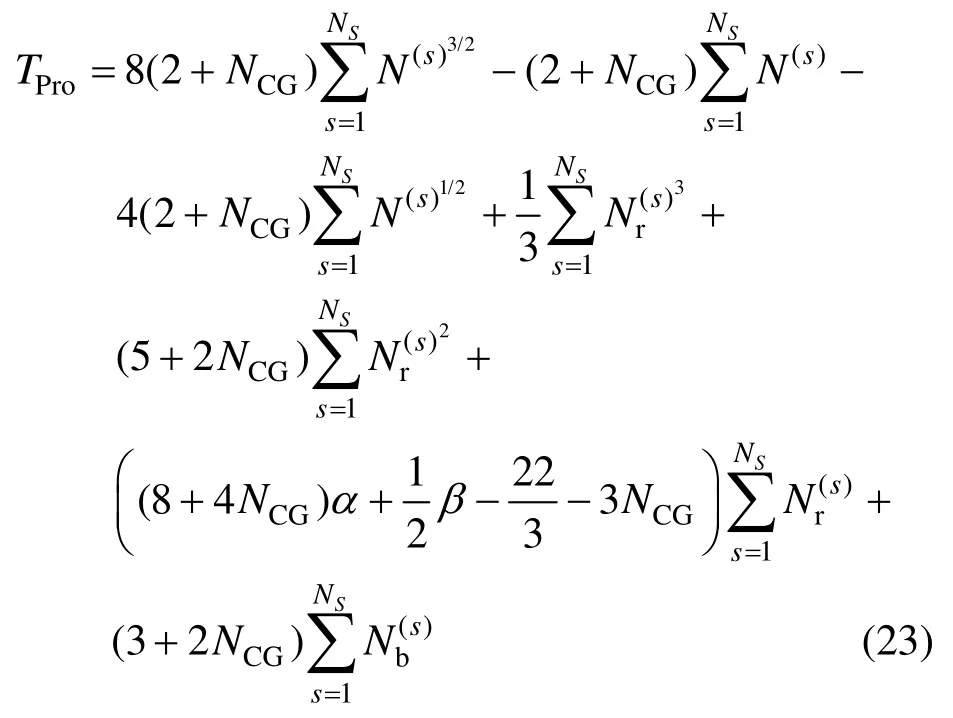
由式(23)可知，界面方程共轭梯度法求解迭代次数NCG和非线性自由度数是影响基于子结构的Woodbury法时间复杂度的重要参数，NCG和越大，该方法的时间复杂度越高，即效率越低。

4 算例

4.1 工程概况

某7层钢框架结构，详细尺寸如图7(a)和图7(b)所示；框架梁柱截面均为工字型，具体信息如图7(c)所示。每根梁和柱沿长度方向被划分为5个单元，共计2940个单元，其类型为3结点Timoshenko梁，结点自由度总数为 15456。所有单元截面的纤维数量均为31根，上、下翼缘各划分11根纤维，中间腹板划分9根纤维。在梁、柱节点处布置集中质量，分布情况见表3。钢材初始弹性模量为Ee=200 GPa，屈服应力为σy=300 MPa，应力-应变关系为线性硬化模型，硬化模量为Eh=0.02Ee。地震波选取台湾集集地震波，输入方向为平面双向，两个方向的峰值加速度均调幅到1.2g。时间间隔为0.01 s，总分析时长为30 s。

表2 基于子结构的Woodbury法的时间复杂度Table 2 Time complexity of Woodbury approach based on substructuring method

图7 7层7跨钢框架Fig.7 Seven-bay seven-story steel frame

表3 梁柱节点集中质量Table 3 Joint masses of structure

4.2 结果分析

为验证子结构数对本文方法计算结果的影响，根据图8所示的剖分方案将整体结构划分为2个子结构，4个子结构和8个子结构三种工况，并分别进行非线性动力时程分析，最终得到三种工况下的顶层位移时程曲线如图9(a)所示。结果表明：基于子结构的Woodbury法三种工况的计算结果基本一致，其相对误差在万分之一以下，即子结构数对该方法计算结果基本没有影响。

为进一步验证本文方法的准确性，分别采用Woodbury法和基于子结构的Woodbury法对该框架结构进行非线性动力时程分析，两种方法计算得到的顶层加速度和位移时程曲线分别如图9(b)和图9(c)所示。结果表明：两种方法的顶层时程曲线基本重合，说明基于子结构的Woodbury法的计算精度与Woodbury法基本一致。此外，在单元的非线性状态判定过程中，可确定某一单元所有非线性插值点处不为0的非线性应变个数，此即为该单元的非线性自由度数；通过统计某一分析步所有单元的非线性自由度数之和，即可得到该分析步结构非线性自由度数，图10给出了所有分析步结构非线性自由度数曲线；为直观反映结构非线性规模，定义非线性占比γ，其为结构非线性自由度数和结点位移自由度数的比值，即γ=Nr/N。由图10可知，结构最大非线性自由度数为1995，此时非线性占比为γ≈ 1 2.9%，而在整个分析过程中，结构平均非线性自由度数为 371，相应的平均非线性占比为γ≈ 2.4%。图11给出了基于子结构的 Woodbury法三种工况下的共轭梯度法迭代次数曲线，由图11可知，随着子结构数的增加，共轭梯度法迭代次数也相应增加，其中，相比2个子结构而言，4个子结构的迭代次数仅在非线性占比较高的分析步增加明显，而8个子结构的迭代次数则几乎在每一分析步均有明显增长。

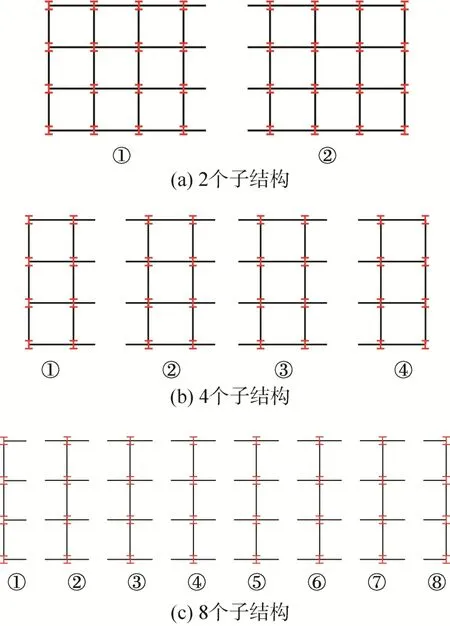
图8 子结构剖分方案Fig.8 Partitioning schemes of substructures

图9 顶层时程曲线Fig.9 Time-history curves of top floor

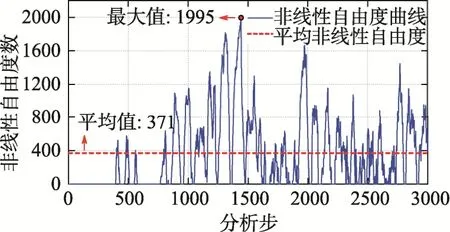
图10 非线性自由度曲线Fig.10 Curves of nonlinear degrees of freedom

图11 共轭梯度法迭代次数曲线Fig.11 Curves of iterations of conjugate gradient method

4.3 效率评价

考虑刚度矩阵带宽与结构结点自由度数的关系，Woodbury法一次N-R迭代求解的时间复杂度TIS为[27]：

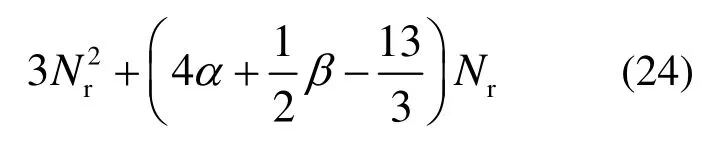
根据非线性分析过程中每一次 N-R迭代步结构非线性自由度数(图(10))以及求解界面方程所需的共轭梯度法迭代次数(图(11))，结合式(24)和式(23)可统计出 Woodbury法和基于子结构的Woodbury法每一N-R迭代步的时间复杂度，表4给出了两种方法的最大时间复杂度和平均时间复杂度，图12给出了基于子结构的Woodbury法三种工况下的时间复杂度曲线。

表4 两种方法的时间复杂度对比Table 4 Time complexity comparison of two methods

图12 时间复杂度曲线Fig.12 Curves of time complexity

由表4可知，基于子结构的Woodbury法的最大时间复杂度和平均时间复杂度均明显低于Woodbury法。值得注意的是，随着划分子结构数的增多，基于子结构的Woodbury法的最大时间复杂度逐渐降低；而平均时间复杂度虽然也有降低的趋势，但8个子结构时的平均时间复杂度要高于4个子结构，其主要原因可结合图10~图12来说明。通过对比图10~图12可知，基于子结构的Woodbury法的时间复杂度随分析步的变化规律与非线性自由度数和共轭梯度法迭代次数(以下简称迭代次数)类似，这再一次说明非线性自由度数和迭代次数是影响本文算法时间复杂度的两个关键因素；通过进一步分析两个因素对每一分析步时间复杂度的影响比重可知，在非线性占比较高的分析步，非线性自由度数起控制作用，此即基于子结构的Woodbury法的最大时间复杂度随着子结构数的增多而递减的主要原因；而在非线性占比较低的分析步，迭代次数起控制作用，此即大多数分析步中8个子结构的时间复杂度高于4个子结构的主要原因。

5 结论

本文基于子结构法有效降低了Schur补矩阵的规模，同时将Woodbury公式应用于各子结构，仅需对子结构Schur补矩阵进行分解，避免了整体结构Schur补矩阵的相应运算；依据时间复杂度理论建立效率模型，并通过数值算例验证了基于子结构的Woodbury法的准确性和高效性。得到的主要结论如下：

(1)与 Woodbury法相比，基于子结构的Woodbury法在保证计算精度的前提下进一步提高了Woodbury公式的计算效率，拓宽了其应用范围；

(2)子结构数对基于子结构的 Woodbury法的计算精度影响极小，但其对该方法计算效率影响较大。为保证本文方法具有较好的计算性能，可根据“界面结点自由度数与结构结点自由度数的比值不超过10%”的经验准则来选取合适的子结构数。

附录：Woodbury公式

Woodbury公式是用来对仅有少量元素变化(低秩修正)的矩阵快速求逆的数学工具。假设某个n×n阶的矩阵A可逆，且其逆已知，A经低秩修正后得到矩阵B，即B=A+WVT，其中W和V均为n×p阶的矩阵，且p远小于n。若矩阵A和(I+VTA-1W)可逆，则矩阵B的逆可通过Woodbury公式进行高效求解[19]，即：

由于A-1已知，式(A1)的主要计算量集中于一个p×p阶的矩阵(I+VTA-1W)的合成和求逆，且低秩修正时，该矩阵的阶数p远小于矩阵B的阶数n(即p<