基于小样本记录的柱面网壳结构地震响应评估

李玉刚，范 峰，洪汉平

(1.西北工业大学力学与土木建筑学院，陕西，西安 710072；2.哈尔滨工业大学土木工程学院，黑龙江，哈尔滨 150090；3.西安大略大学土木与环境工程系，加拿大，伦敦 N6A 5B9)

单层柱面网壳结构因其自重轻、结构刚度好以及相对易于建造等优点，使其在诸如火车站、航站楼、展览馆等公共建筑中获得了广泛应用，比如青岛客站无站台柱风雨棚既采用单层柱面网壳结构形式[1]。学者们采用数值模拟或试验等方法对单层网壳结构的静力和动力性能进行了深入的研究[2―12]。沈世钊[2]即对网壳结构的稳定性和抗震性能做了详细的介绍。朱钊辰等[3]基于反演推定的概念，提出了适用于空间结构的随机缺陷传播算法。叶继红等[4]提出了离散元塑性区法，并对单层球面网壳结构进行了弹塑性屈曲分析。陆明飞等[5]基于易损性理论中的构形度概念，引入几何刚度矩阵考虑荷载模式、荷载幅值、约束及非线性等因素，从构形度变化特性上揭示了网壳的失稳机理。Li和Chen[6]提出一种适用于单层网壳结构的非线性地震响应计算方法。支旭东等[7]研究了强震作用下单层球面网壳结构的失效机理和易损性。Yu等[8]研究了下部支承对整体结构地震反应的影响，而李玉刚等[9]在此基础上又考虑了地震动空间变化性对结构反应的影响。马会环等[10]通过缩尺模型试验研究了半刚性节点对单层柱面网壳结构的影响。刘海峰等[11]研究了焊接球节点刚度对网壳结构有限元分析精度的影响。陈兆涛等[12]研制一种三维隔震装置，对比分析了不同地震作用下单层球面网壳结构在不隔震、水平隔震、非变刚度三维隔震与竖向变刚度三维隔震时的地震反应。

对单层球面网壳进行数值分析结果表明[13]，与采用时程分析法获得的峰值响应平均值相比用CQC法估计单元内力将导致显著误差。这在一定程度上可以归因于网壳结构频谱密集和杆件内力受高阶振动模态的影响，同时也指出为降低由地震动记录间差异引起的结构反应的变异性，对于不同的结构反应合适的地震动强度参数也不同。考虑GB50011―2010《建筑抗震设计规范》所规定的选择3或7条地震动记录的准则，对获得的结构响应进行统计分析表明，选用7条地震动记录的准则可减少结构抗震设计需求的偏差。然而，这些结论能否直接应用于诸如柱面网壳等其它类型网格结构还是未知的。

为减少结构地震时程分析计算时间进而促进工程实践，抗震设计规范[14―16]在需要采用时程分析法进行结构设计或校核时，规定了选取最少地震动记录数量的通用准则。按规范要求选择的一组地震动记录在调幅之后应该与设计反应谱相匹配，采用调幅后地震动记录作用下结构反应的平均值或包络值。同一程度地震灾害可分解为不同震级和震中距的组合，并且地震记录间存在变异性，因此造成了在地震动记录选择中的困难[17―20]。此外，规范中所规定的最少地震动记录数量是基于工程经验而不是全面的统计分析[21]，并且小样本地震动记录对多自由度体系地震反应统计值的影响也没有讨论。

本文以单层柱面网壳结构为研究对象，比较反应谱法和时程分析法计算的结构反应，评估由于地震动记录数量限制引起的结构反应的不确定性，分析地震动强度参数的适用性以降低由于记录间差异引起的结构最大反应的变异性。对于时程分析，选用了166条实际地震动记录，而用CQC法计算结构反应时是基于设计反应谱和调幅后记录的平均反应谱，对计算结果进行统计分析，以期指导工程实践来选择适用于柱面网壳抗震设计的最少地震动数量和计算方法。

1 结构模型和地震动记录

1.1 柱面网壳结构模型

选用三向网格型柱面网壳，支承为纵向边缘落地固定铰支座，采用瑞利阻尼，阻尼比取 0.02。JGJ7―2010《空间网格结构技术规程》中规定[22]：沿两纵向边支承的单层柱面网壳跨度不宜大于30 m，矢高可取跨度的1/2~1/5。所以本模型跨度取30 m，矢跨比取1/4，长度取42 m，几何模型如图1所示。采用通用有限元软件ANSYS进行数值模拟，用 PIPE16单元模拟网壳杆件，每根杆件划分为3个单元。PIPE16单元是具有拉压、弯曲和扭转性能的单轴单元，每个节点有6个自由度，网壳节点为刚接。MASS21单元模拟集中在节点上的屋面质量。弹性模量E=2.06×105N/mm2，泊松比v=0.3，密度ρ=7850 kg/m3，质量分布为120 kg/m2，考虑了1000 N/m2恒荷与400 N/m2雪荷，模型其它参数见表1。

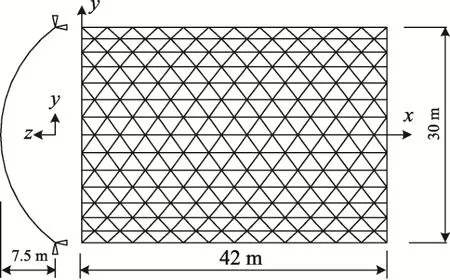
图1 单层柱面网壳计算模型Fig.1 Analysis model of single-layer cylindrical latticed shell

对结构进行模态分析表明，柱面网壳的频谱十分密集(见图2(a))，前100阶频率分布在0.867 Hz ~23.271 Hz，前3阶自振周期(用T1、T2和T3表示)分别为1.15 s、0.48 s和0.45 s。第1阶模态为沿跨度方向(y向)的水平振动，第2阶模态频率为竖向振动，第3阶模态为沿长度方向(x向)的翘曲振动。

表1 单层柱面网壳参数Table 1 Parameters of single-layer cylindrical latticed shell

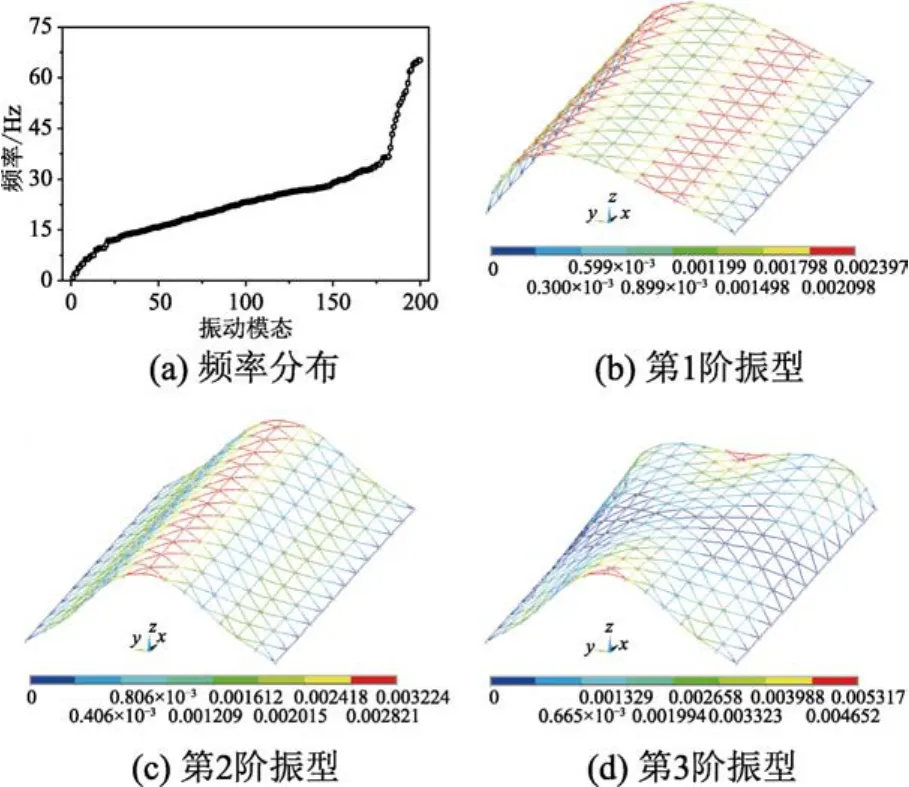
图2 结构的自振频率与振型Fig.2 Natural vibration frequency and illustration of shapes of selected vibration modes

首先，结构是按照静力(恒荷载和雪荷载)稳定性进行设计，初始几何缺陷分布采用结构的最低阶屈曲模态，缺陷最大计算值为 0.1 m(即跨度的1/300)[22]。取场地类别为II类，设计地震分组为第3组。由线弹性抗震设计校核可知结构足以满足目标PGA为140 cm/s2(即9度设防下的多遇地震)的设计谱作用下的抗震需求，设计谱如图3(a)所示，在T1和T3处的SA分别为159 cm/s2和398 cm/s2。

图3 调幅后地震动记录的反应谱和设计谱Fig.3 Design spectrum and response spectra for scaled records

1.2 地震动记录选择

从中国地震动数据库中选择记录对本文来说是比较理想的，但有效的中国历史地震动记录相对缺乏并且与记录台站相关的信息不是都很详细。因此，本文选择的地震动记录均来源于美国地震动数据库NGA(http://peer.berkeley.edu/nga/ search.html)。给定地震灾害或风险度量可以分解为不同的震级和震中距的组合，选择地震动记录的震级应在所考虑震级 ± 0.25级的范围内，震中距应该在所考虑震中距 ± 25 km范围内[23－24]。这一条件有可能过于严格，限制了可以选择的历史地震动记录数量。考虑到本研究集中于结构抗震设计的荷载效应，在选择记录时采用了较宽松的标准，以期获得足够的地震动记录数量用于网壳结构地震反应的统计分析。

在下面的数值分析中，从NGA数据库中选择了83条记录[13]。选择标准包括：a)矩震级大于6级；b)震中距从20 km ~ 200 km；c)NEHRP场地类别为C类和D类的记录，与中国规范II场地类别对应。此外，不同位置的记录认为是相互独立的，每个记录的两个水平分量也认为是相互独立的[25]，因此共计有166条水平记录分量。

按 PGA=140 cm/s2(对应 9度设防下的多遇地震)调幅后地震动记录的反应谱如图3(b)所示。结构最低阶沿跨度方向振动模态和最低阶沿长度方向振动模态的周期分别是T1和T3，所以在沿跨度方向和长度方向进行一维地震激励时，按反应谱调幅的目标值分别为SA(T1)=159.4 cm/s2和SA(T3)=397.6 cm/s2，调幅后地震动记录的反应谱如图3(c)、图3(d)所示。由图显而易见地震动记录间的差异非常显著。记录按 PGA调幅后的反应谱的标准差在频域内是相似的，而基于指定周期处SA值调幅后的反应谱值在离指定周期越远处标准差越大，这与文献[26]是相符的。

为便于说明，图3(b)、图3(c)和图3(d)所示的平均反应谱分别将用 MRS-PGA，MRS-SA-1和MRS-SA-2表示。这些谱也和166条记录用于下文中的结构反应计算。

2 柱面网壳地震反应估计

2.1 采用反应谱法计算结构地震反应

对于抗震设计，结构杆件尺寸的选择是采用线弹性反应，应用叠加原理对不同类型荷载效应进行组合。因此，除特别说明外，下文中的结果均是基于线弹性地震反应。

针对沿跨度方向的地震激励，在设计谱作用下采用 CQC法计算的结构节点位移和杆件轴力如图4(a)，图4(b)所示。需要指出的是，JGJ7―2010《空间网格结构技术规程》规定至少取前25阶~30阶振型参与组合[22]，本文为考虑高阶模态的影响，在振型组合时考虑了前 200阶振型。类似的，沿长度方向激励获得的结构反应如图4(c)、图4(d)所示。图4(a)表明最大节点位移分布与第1阶振型(见图2(b))相一致，而最大杆件轴力分布(见图4(b))不同于最大节点位移，这是因为杆件轴力与节点位移不直接相关，而是取决于节点间的相对位移。图4(c)中的最大节点位移分布与结构的第 3阶振型(见图2(d))相符，最大杆件轴力的位置(见图4(d))也不同于图4(c)中的最大节点位移。

图4 反应谱法计算的结构反应Fig.4 Calculated response using response spectrum method

使用 166条地震动记录获得的 MRS-PGA，MRS-SA-1和 MRS-SA-2与设计谱不同。用MRS-PGA，MRS-SA-1和MRS-SA-2替换设计谱重复上述计算，对于跨度方向的激励应采用MRS-PGA或 MRS-SA-1，对于长度方向的激励应采用MRS-PGA或MRS-SA-2。为观察由用不同地震反应谱所引起反应间的差异，从这些分析结果中提取所需的结构反应，如表2、表3所示。其中：D为最大节点位移；AF1为纵肋和横杆中的最大轴力；AF2为斜杆中的最大轴力；SBS为最大支座基底剪力；SBT为最大基底剪力和；SBS和SBT的方向与地震激励方向相同。由表可知，结构的最大反应取决于采用的反应谱。对于跨度方向的激励，采用MRS-PGA 反应谱获得的D、AF1、AF2、SBS和SBT的值大于设计谱或 MRS-SA-1，这归因于在结构较低自振频率范围内MRS-PGA的值大于设计频谱或MRS-SA-1，而在跨度方向激励的结构反应对低频是非常敏感的。分别采用MRS-SA-1反应谱和设计谱获得的结构反应值是相似的，这符合预期，因为在影响柱面网壳结构跨度方向振动的周期范围内的设计谱值与MRS-SA-1几乎相等。

表2 跨度方向激励的CQC法和时程分析法的计算结果Table 2 Calculated results based on CQC rule and time-history analysis for transversal excitations

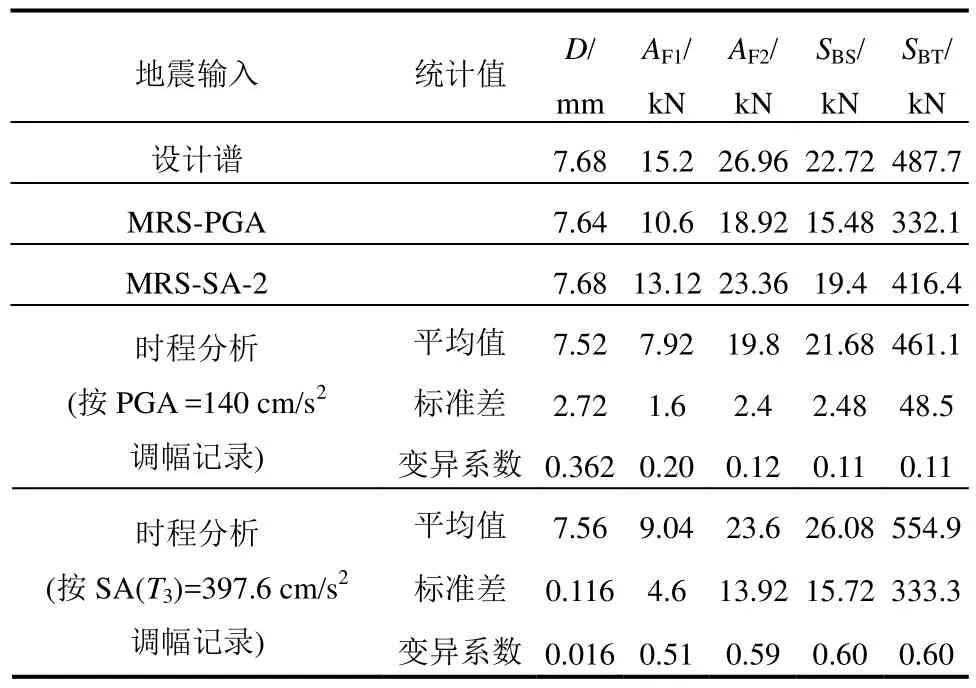
表3 长度方向激励的CQC法和时程分析法的计算结果Table 3 Calculated results based on CQC rule and time-history analysis for longitudinal excitations

对于长度方向的激励，无论采用 MRS-PGA、MRS-SA-2还是设计频谱获得的D值都是相似的，这是因为D值受纵向振动模态周期T3=0.45 s处的反应谱值控制，而这3个反应谱在该周期处的值几乎相同。采用 MRS-PGA 获得的AF1、AF2、SBS和SBT要小于另外两种情况，这是因为在T< 0.16 s的范围内MRS-PGA的值小于设计谱和MRS-SA-2，而在长度方向激励下AF1、AF2、SBS和SBT等值受局部高阶振型影响较大。

综上所述，可推断柱面网壳的最大节点位移受低阶振动周期处的反应谱值控制，而对于结构杆件内力和支座反力来说高阶振动模态的影响不容忽略。

2.2 时程分析法计算结果的统计分析

图3所示地震动记录的反应谱是各不相同的。这种差异将影响像网壳一样复杂的结构系统的地震反应。为分析由不同地震动记录引起的结构响应间的统计差异，对记录分别按PGA、SA(T1)和SA(T3)进行调幅(见图3(b)、图3(c)、图3(d))，采用时程分析法分别计算了166条地震动记录沿跨度方向和长度方向作用下柱面网壳结构的地震反应。从时程分析结果中提取D、AF1、AF2、SBS和SBT等值。这些值与 CQC法获得的结果进行对比的平均值、标准差和变异系数见表2、表3。由表可知采用PGA调幅地震动记录所获得的AF1、AF2、SBS和SBT等值的变异系数小于采用SA调幅的结果，而对于D值却恰好相反。这意味着对于结构设计所需的杆件轴力和支座反力来说，采用 PGA调幅地震动记录是较好的，因为这可以降低反应的离散性。但如果所需的是结构的最大节点位移，那么采用SA则是较合适的。

从表中还可知，基于 PGA调幅后时程分析法获得结构反应的平均值与采用MRS-PGA谱和CQC法计算结果有明显差异。对于跨度方向的激励，D值的差异非常小，而AF1、AF2、SBS和SBT的差异有8%~15%。如果激励是沿长度方向，那么D值的差异是 2%，对于AF1、AF2、SBS和SBT来说差异在4%~38%。如果将调幅目标由PGA换成SA，对AF1、AF2、SBS和SBT来说可得以上类似结果。这表明对于柱面网壳来说无论是输入设计谱还是调幅后记录的平均谱，采用 CQC法估算结构地震反应需求都不是非常恰当。

2.3 采用3条或7条记录对结构反应统计的影响

GB50011―2010《建筑抗震设计规范》规定了采用时程分析法时选择3条或7条地震动记录的准则。如果选择3条地震动记录并按PGA调幅至目标值，则规范规定[12]：1)调幅后地震动记录在主要振型周期处的反应谱均值与规范反应谱间的差异不应小于20%；2)每条地震动记录计算所得结构基底剪力不应小于振型分解反应谱法(采用设计谱)计算结果的65%；3)3条地震动记录计算所得结构基底剪力的平均值不应小于振型分解反应谱法(采用设计谱)计算结果的80%；4)采用3条记录时程分析计算所得结构反应的包络值；5)对于抗震设计，需要采用4)中的值和基于设计谱的振型分解反应谱法计算结果两者中的较大值。

对基于小样本记录所得结构反应进行统计分析，在上述标准中用设计谱计算结果是不合适的，因为设计谱与调幅后地震动记录的平均反应谱不同(见图3)。为避免由于反应谱的不同引起结构反应的差异，选取准则中的设计谱将用平均反应谱取代。采用文献[13]中的抽样方法从 166条记录中选取3条记录共计1000次。对于每组中的3条记录分别输入柱面网壳结构进行时程响应分析，提取AF1、AF2、SBS和SBT，取3条记录作用下结构反应的包络值用AF1-3、AF2-3、SBS-3和SBT-3表示，即AF1-3、AF2-3、SBS-3和SBT-3为考虑条件1)~ 4)后获得的结构反应。对于抗震设计，一般不用D值进行杆件截面选择，所以在本节中没有对采用3条或7条记录准则获得的D值进行统计。

图5 在跨度方向激励下考虑3条记录基于PGA调幅获得结构反应的统计值和直方图Fig.5 Histograms and statistics of responses by considering three records and scaled by PGA for transversal excitation

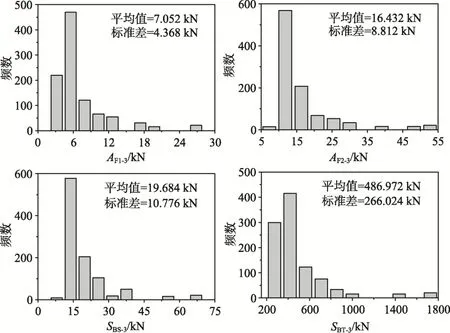
图6 在跨度方向激励下考虑3条记录基于SA调幅获得结构反应的统计值和直方图Fig.6 Histograms and statistics of responses by considering three records and scaled by the SA for transversal excitation

对于跨度方向激励，采用PGA调幅获得的1000个AF1-3、AF2-3、SBS-3和SBT-3样本以直方图的形式展现在图5中，采用SA调幅后样本的直方图见图6。计算样本的平均值、标准差和变异系数如表4所示。

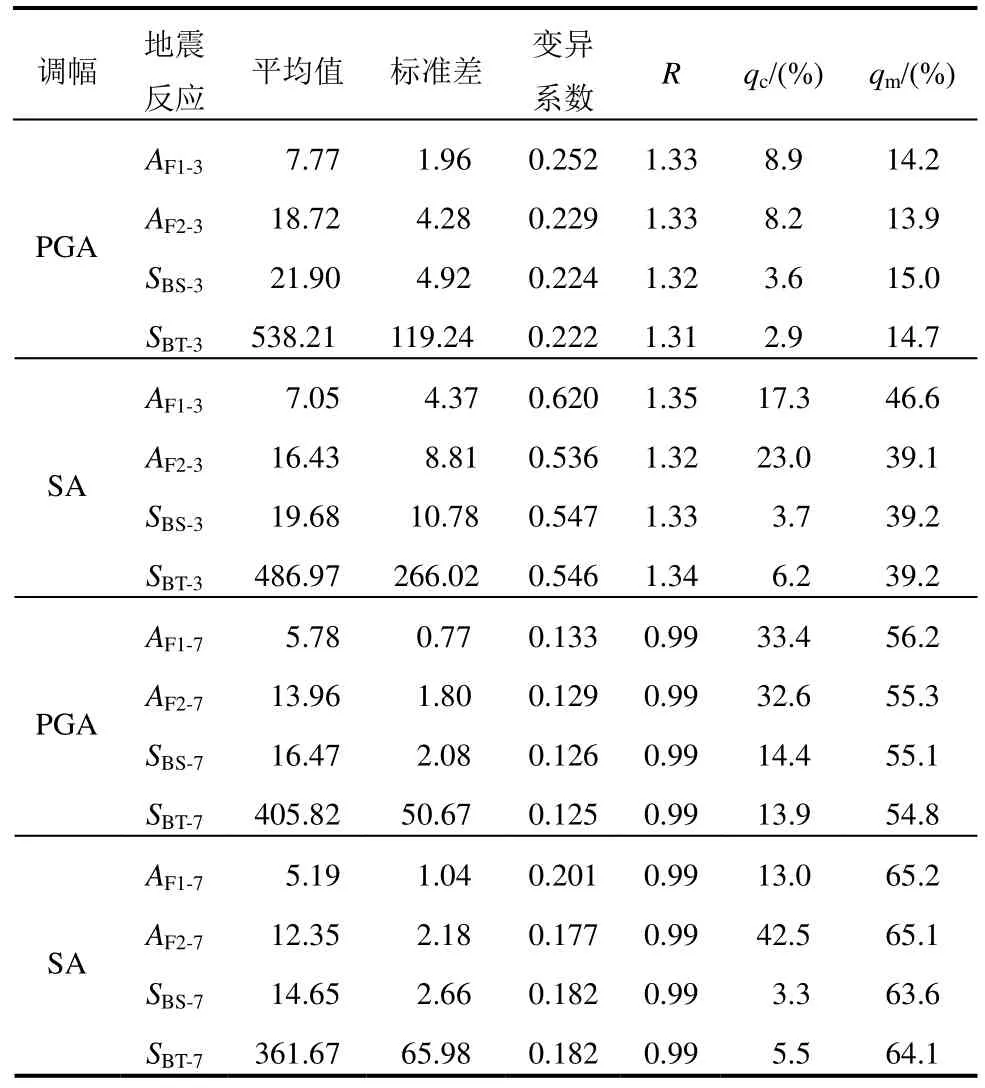
表4 在跨度方向激励下考虑小样本记录的1000个样本的统计Table 4 Statistics of the responses by considering small number of records and 1000 replicas under transversal excitation

对比图5和图6中的结果可知，采用不同目标值调幅获得的地震反应具有明显差异。采用 PGA调幅的直方图大概呈对称形态，而采用SA调幅的直方图则不具有对称性，表明基于不同参数调幅地震动记录将使过高估计或过低估计结构反应的概率有较大差异。为分析小样本地震动记录对结构反应估计的影响，计算了采用小样本和大样本地震动记录获得的结构反应均值之比，用R表示。所得R值同样列于表4中。由表可知R值始终大于1，这意味就平均值而言，应用按规范条件选择的3条记录将导致地震反应估计的较大偏差。由表中的统计值可知，基于PGA调幅后考虑条件1)~ 4)获得的结构反应的变异系数小于基于SA调幅后的结果，这也说明，如果所需的是杆件内力或支座反力则采用PGA调幅地震动记录是较合适的。

用qc表示考虑条件1)~ 4)获得的结构反应小于CQC法计算结果的百分比，用qm表示考虑条件1)~4)获得的结构反应小于166条记录的结构反应均值的百分比，计算qc和qm并将结果一并列于表4。由表4可知采用PGA调幅qc和qm的值不超过9%和15%，如果采用SA调幅qc和qm分别小于23%和47%。这些结果反映了考虑选取条件采用3条记录准则将过高地估计地震效应，这也反映了图6中的右偏分布。

需要注意的是，计算AF1-3、AF2-3、SBS-3和SBT-3时选择地震动记录准则中没有考虑条件5)。同时考虑条件1)~ 5)则可以保证获得的结构反应大于或等于CQC法计算的结果。此外，表4给出的变异系数是考虑3条记录准则获得结构反应的包络值或考虑7条记录准则获得结构反应的平均值，不应该将这些变异系数值直接与表2中的结果进行比较。因为表2中的变异系数是针对随机选择的单个记录。总之，从表3的结果可知，规范中选择地震动记录条件1)~ 4)相对于没有小样本容量影响的平均结构反应来说过于严格和保守。

图7 在跨度方向激励下考虑7条记录基于PGA调幅获得结构反应的统计值和直方图Fig.7 Histograms and statistics of responses by considering seven records and scaled by PGA for transversal excitation

图8 在跨度方向激励下考虑7条记录基于SA调幅获得结构反应的统计值和直方图Fig.8 Histograms and statistics of responses by considering seven records and scaled based on SA for transversal excitation

前面已提及，设计规范中也允许使用至少7条记录来计算结构的地震反应，在这种情况下，规范要求仍采用之前的条件1)、2)、3)和5)，条件4)变更为采用选择的地震动记录时程分析结果的平均值。

用7条地震动记录准则代替3条地震动记录准则重复上述分析，获得的结果如图7、图8和表4所示。表中结果表明在这种情况下R值趋近于1，如果采用PGA调幅，qm接近于55%，如果换做用SA调幅qm则增加到65%。这再次说明，采用7条地震动记录准则用于抗震设计可以减小估计的偏差。

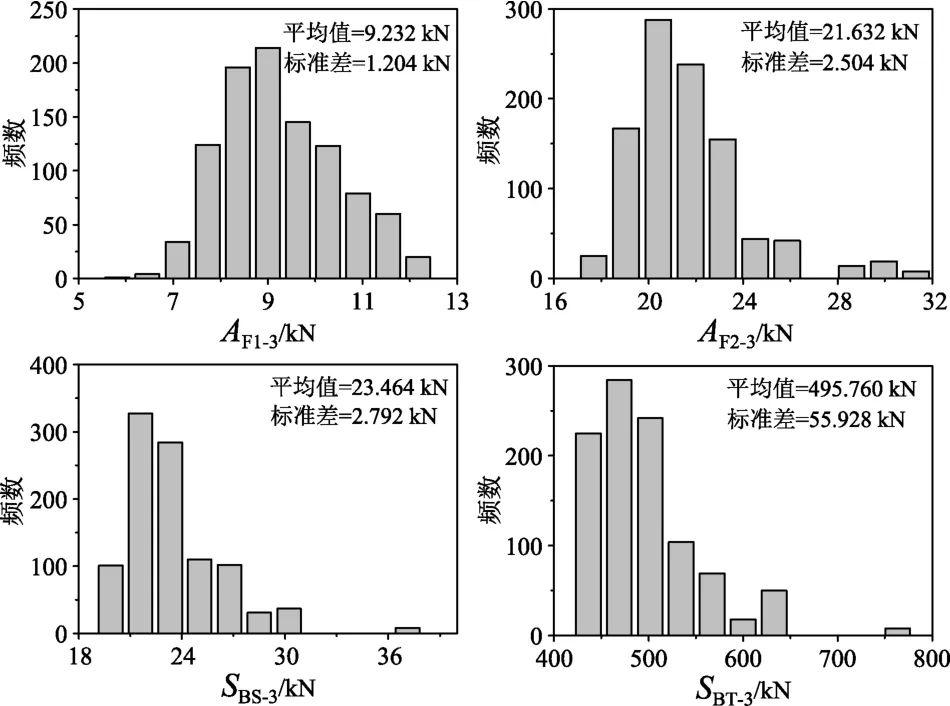
图9 在长度方向激励下考虑3条记录基于PGA调幅获得结构反应的统计值和直方图Fig.9 Histograms and statistics of responses by considering three records and scaled by PGA for longitudinal excitation

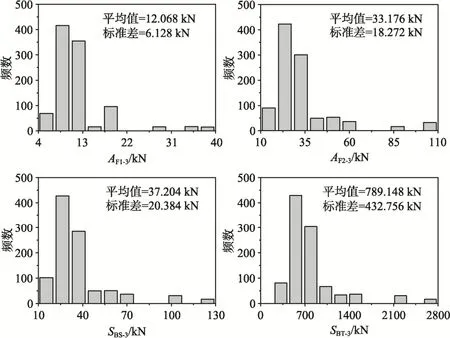
图10 在长度方向激励下考虑3条记录基于SA调幅获得结构反应的统计值和直方图Fig.10 Histograms and statistics of the responses by considering three records and scaled based on SA for longitudinal excitation

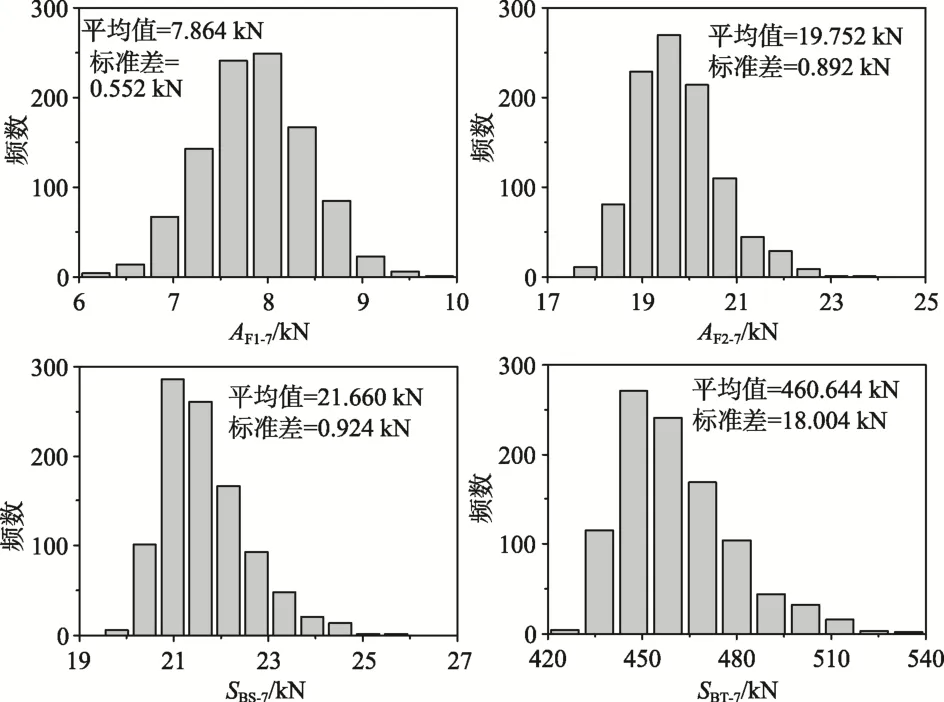
图11 在长度方向激励下考虑7条记录基于PGA调幅获得结构反应的统计值和直方图Fig.11 Histograms and statistics of responses by considering seven records and scaled by PGA for longitudinal excitation

图12 在长度方向激励下考虑7条记录基于SA调幅获得结构反应的统计值和直方图Fig.12 Histograms and statistics of responses by considering seven records and scaled by SA for longitudinal excitation

表5 在长度方向激励下考虑小样本记录的1000个样本的统计Table 5 Statistics of responses by considering small number of records and 1000 replicas under longitudinal excitation

对于沿长度方向的激励也进行了和跨度方向激励一样的分析，结果如图9~图12和表5所示。观察结果表明，跨度方向激励情况下获得的结论也同样适用于长度方向激励的情况。这说明相对于按照无小样本容量影响或 CQC法计算的反应，采用按规则选用 3条记录(准则)的结构反应进行设计是保守的。

3 结论

分别采用反应谱法和时程分析法计算了单层柱面网壳结构的地震反应，用时程分析法时分别考虑了有无小样本容量的影响。该型结构的一个典型特征是频谱十分密集。对于时程分析，分别考虑了采用SA和PGA调幅地震动记录。从获得的柱面网壳结构地震反应的统计结果，可获得主要结论如下：

(1)计算柱面网壳结构抗震设计需求时，按规范选择3条地震动记录准则获得的结果过于保守，采用选择7条地震动记录准则相对来说较为合适。

(2)对于结构构件内力或支座反力来说，使用PGA调幅记录要优于SA，然而，如果所需的是位移，结果恰好相反，即对于不同的结构反应较优的地震动强度参数也随之而不同。

(3)采用 CQC法计算结构的杆件内力和支座反力需求不是非常恰当，采用更多数量的模态参与组合来估计杆件内力和支座反力结果会有所改善，但与时程分析法计算结果的差异仍然是不能忽略的。