周期结构带隙的能效观点

周　俊，饶柱石，塔　娜（.上海交通大学振动、冲击、噪声研究所，上海0040；.上海交通大学机械系统与振动国家重点实验室，上海0040）



周期结构带隙的能效观点

周俊1，饶柱石2，塔娜2
（1.上海交通大学振动、冲击、噪声研究所，上海200240；2.上海交通大学机械系统与振动国家重点实验室，上海200240）

摘要：在几何构型或材料特性方面具有空间重复特性的一类结构，称为周期结构，如桁架、加强筋板等。在一定频率范围内，周期结构能够阻断弹性行波在其中传递，该特性可应用于隔振器开发。现有周期结构隔振分析大多基于无限长假设，即假设周期结构在几何空间中可无限延伸，因此只有行波解具有物理意义，非行波模式则被忽略。然而，工程中隔振系统都是有限长的，因此非行波解的确存在，故其能量传输特性具有研究价值。周期桁架有限元数值仿真结果表明，周期结构行波解的功率因数始终等于1，说明频散曲线与能量传输效率有关。据此引入效率指标函数，通过其响应表面局部极大值、极小值的连线，将频率-波数空间划分为能量传输高效区和低效区。该划分方式能统一处理行波解和非行波解的情况，拓展原有带隙分析适用范围，为有限周期结构能量传输效率分析提供新途径，对于隔振器开发设计具有重要参考价值。

关键词：振动与波；周期结构；功率因数；效率；带隙；桁架

周期结构理论起源于牛顿在计算声速时所引入的一维弹簧振子链模型[1]，随后在多个物理学分支中被广泛应用，例如金属导电性问题[2]。所谓周期结构，就是指一类具有单元重复特性的结构，例如晶体就是由晶胞在空中重复阵列而形成的。此类结构最为重要的特性之一就是对某些频率的行波（光波、弹性波等）具有阻断作用，或者说特定频率范围内的行波，在周期结构中无法传递，该特定频率范围称为带隙、阻带、禁带。对于宏观周期性固体结构，例如桁架、铁轨、加强筋板等，对固体中的弹性波能形成带隙，因此，在振动噪声控制领域，周期结构被视为一种有效隔振手段，受到广泛关注和研究[3- 5]。Bondaryk对周期桁架隔振特性进行研究，证实其具对弹性波具有低通滤波器特性，能较好地抑制高频振动传递[6]。黄修长等设计具有较低阻带中心频率的曲梁周期结构，可用于机械设备隔振支撑[7]。肖勇等对具有周期减振支撑的管道的弯曲波带隙特性及其形成机制进行深入研究，指出通过调节减振支撑间距与参数，可以使局域共振带隙与布拉格带隙发生耦合，从而有效拓宽阻带频率范围[8]。尹剑飞等将周期结构能量隧穿效应纳入周期加强筋板的统计能量分析中，从而提高了子系统响应预测精度[9]。Mei等将周期结构带隙与局域共振原理结合，设计一种薄膜式声超材料，其对空气中低频噪声具有强烈吸收作用[10]。Yan等设计由混凝土包覆、内嵌橡胶和铁芯的元胞，由元胞组成的三维周期性地基，可用于上层建筑物抗震[11]。Wang等利用屈曲状态下梁刚度可变这一特性，实现了带隙中心频率可调节的周期结构[12]。

周期结构隔振特性分析的一般步骤是：首先计算无限长周期结构的带隙[13]，从而确定振动传递的衰减频率范围，然后在有限周期结构上，根据具体边界条件，计算振动传递率，确定有限长情况下的振动衰减量以及衰减频率范围。在振动带隙分析中，以行波解为主，忽略振幅随空间程指数衰减的倏逝波解——近场解。然而，现实中隔振系统都是有限长的，因此倏逝波解的确存在，对振动传递特性必然产生一定影响，例如隧穿效应[14]，所以有必要对周期结构非行波解的能量传输特性做进一步研究。

利用有限单元法，对有限周期桁架在一般情况下的能量传输效率进行计算，通过效率指标函数响应表面[15]的局部极大值、1/2局部极大值以及极小值分布，将频率-波数空间，划分为一系列能量传输高效区和低效区（对应隔振区）。上述划分方式为有限周期结构的能量传输特性分析提供新途径和视角，对隔振器的设计和开发具有重要参考价值。

1　带隙理论回顾

1.1一维纵波

为了与周期结构中行波解作对比，不妨首先回顾均匀介质中的一维纵波。众所周知，等截面细长杆中的单列纵波解可表示为

式中v表示纵向振速，谱系数vˆ表示波幅以及相位。令杆中横截面的纵向拉力N为

上式中cL为纵波波速，负号是由于截面正应力取拉为正造成的。该式表明，右行波解的截面内力与纵向速度之间的相位相差180°，注意到截面拉力N所做的时均功率P¯计算式为

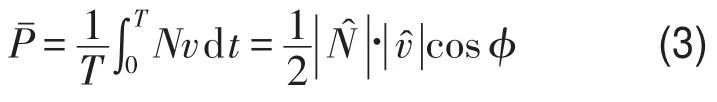
式中cosϕ称为功率因数。

根据以上讨论可以得出行波解具有如下两个重要特性：

特性1.由式(1)和式(2)可知，沿波传播方向上，截面状态变量(力、速度等)幅值相等，且滞后的相位差相同，即

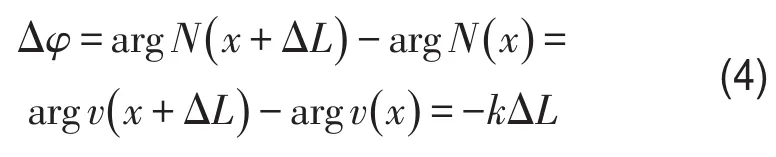
式中N和v如图1所示。

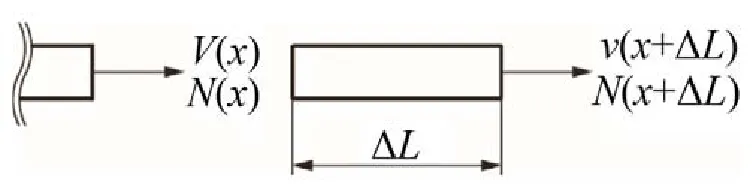
图1　截面状态变量

特性2.由式(2)和式(3)可知，截面内力功率的功率因数等于cosϕ=∓1，换句话说，行波解是以最大效率的方式传输能量（行波解内力所做的无工功率为零）。需要说明的是：特性1和2之间是相互独立的。特性2与应力-应变关系有关，无法由特性1直接推出。

除了从功率因数角度衡量能量传输效率以外，还将引入效率指标η来衡量传输过程中所需付出的能量代价问题。注意到功率是力与速度的乘积，满足传输功率不变的前提下，如果输入端驱动力过大，容易诱发承载件的疲劳破坏，影响使用寿命；另一方面，如果驱动力不大，但输入端振速过大，则意味着浪费在粘滞损耗上的功率在加大，换句话说，输入端所需付出的动能和应变能之和越小越好。因此，可以将功率与输入端比机械能（单位质量的机械能）之比作为另一种能量传输效率指标

相比于功率因数，指标η还考虑了输入端驱动力和速度，因此是一个综合性能指标。注意到纵波时均功率计算式为以及

代入式(5)得到单列纵波的效率指标η=1。指标η的物理意义是：在输入端，每增加单位比机械能，传输功率的提高量为ρAcLη，显然η越大，相同传输功率条件下，在输入端所需维持的场能越小。进一步可以证明，如果存在反射波，则η<1，这意味单列行波模式具有如下特性：

特性3.单列行波解的能量传输效率指标η取到最大值。

由一维纵波特性2和3可知，从能量传输效率角度，行波解具有显著地位。那么对于周期结构中的行波解，是否也具有特性2和3则有待进一步验证。

1.2周期结构带隙

在周期结构中，如果在某些频率范围内找不到行波解，说明振动能量的传递在此频带内受到抑制，这一特殊频率范围就是所谓带隙。以图2所示的一维周期结构为例，假定其两侧均可无限延伸，现截取若干个元胞（周期）作隔离体分析，并令左侧为输入端，右侧为输出端。设输入/输出端的简谐内力和振速分别为和

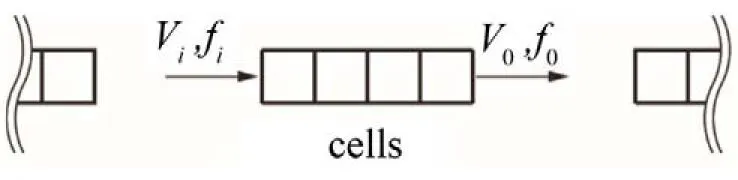
图2　一维周期结构示意图.

一维周期结构行波解的判定准则如下[16]

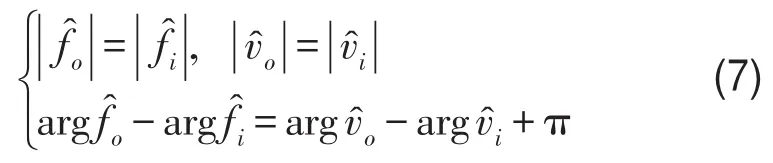
式中+π的原因是由于输入/输出端截面外法线方向不一致造成的，该判定准则本质上等价于行波特性1。需要注意的是，单纯依靠式(7)同样无法判定周期结构行波解的功率因数cosϕ是否一定等于1。

令图2中隔离体的输入/输出端的振速幅值比为λ

根据判定准则式(7)可知，λ=1是周期结构行波解的必要而非充分条件，换句话说满足λ=1的解并不一定就是行波解。在某些情况下，驻波解同样可以满足λ=1的条件；除行波解外，周期结构还可存在倏逝波解，此类解的特点是波幅随空间坐标增加而指数增长或衰减，显然此时λ≠1。

如果采用无限周期结构假设，这意味着倏逝波解不具有物理意义。事实上，倏逝波解的振速幅值将在正或负无穷远端发散，因而通常不予考虑。然而，对于一般工程结构，无限周期假设并不十分恰当。注意到工程结构都是有限长的，无限周期假设仅仅是一个理想假设，因此在应用周期结构带隙特性进行隔振器开发设计过程中，如果完全排除λ≠1的振动传递模式而仅考虑行波解，则无法全面地描述有限长周期结构的动态特性。因此，下面将对非行波解的能量传输的效率问题做进一步探讨。

由纵波的讨论可知，功率传输效率高低可以用输入端所需的总能大小来衡量。对于周期桁架结构，其效率指标η不妨定义为如下形式

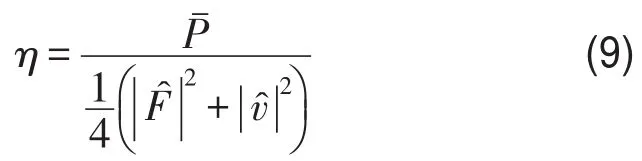
首先，根据式(3)，注意到时均功率可表示为谱系数点乘的形式

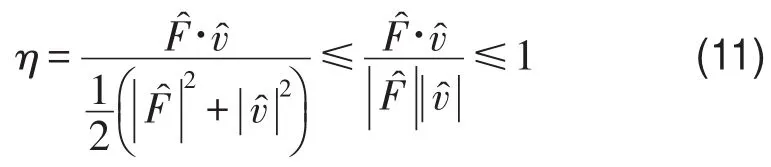
式(11)表明，按式(9)所定义效率指标最大值不超过1（有上界），因此确实可以作为一种效率指标。引入该指标的好处是可以更全面地反映周期结构能量传输特性。

对于非行波解，如果指定输入/输出端的振速幅值比λ及其相位差，则不同频率下的效率值η将是个确定值，因此η是关于λ、Δφ和ω的三元函数

若固定λ，η函数可表示成一张二维曲面，称为响应表面；当λ变化时，将形成一系列曲面簇。利用响应表面的局部极大值和极小值分布情况，就可以表征不同状态下的能量传输效率。下面将针对有限周期桁架结构的传输效率问题进行仿真计算。

2　数值仿真

有限周期桁架计算模型如图3所示。桁架类型为布朗型（Brown）。为了简单起见，各杆件规格统一为：空心圆钢管，外径×壁厚=38 mm×3 mm。

在数值仿真中，输入/输出端采用位移激励，并假定截面位移是均匀的，所以边界条件为

图3　有限周期桁架计算模型

下面首先研究行波解的情况。

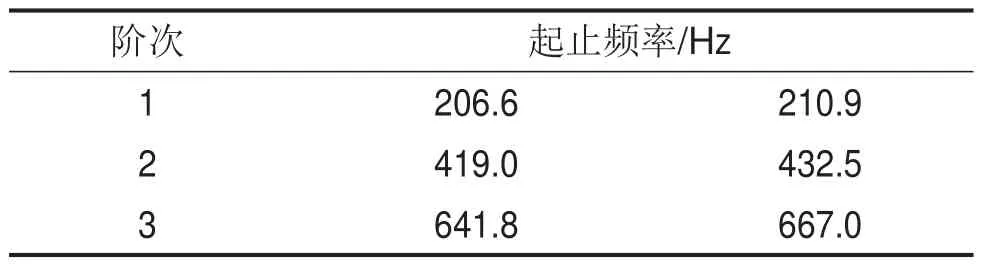
表1　桁架带隙频率

均匀媒质中的纵波特性2表明行波解的功率因数为1，那么周期结构中的行波解是否也存在上述特性？答案是肯定的，下面通过数值仿真的方式予以证明。

首先注意到行波解的λ=1，换句话说此时的功率因数cosϕ仅与输入输出端振速相位差Δφ和角频率ω有关，因此功率因数可视为关于频率和输入/输出端相位差的二元函数，在三维空间中可以绘制出一张曲面——功率因数响应表面：。需要特别说明的是，该响应表面给出λ=1时所有振动传递模式的功率因数。将响应表面的最大值（cosϕ=1）连线——形成所谓“脊线”，并向Δφ-ω平面投影，如果脊线的投影曲线与频散曲线重合，则表明在λ=1的所有可能解中，仅有行波解能取到cosϕ=1。

为了证明这一点，不妨用平面Δφ=φi作为横截面，与功率因数响应表面相交，所得横截曲线如图4 (b)所示。该曲线簇反映不同相位差下，功率因数随频率变化情况。对比图4(a)和图4(b)可知，给定输入输出端相位差Δφ，功率因数等于1的频率恰好就是存在行波模式时的频率。这就证明了在周期结构中，仅有行波模式能够以最大功率因数方式传输能量——与均匀媒质中纵波特性2保持一致。上述现象也说明周期结构中行波解的确是均匀媒质中弹性波一种推广。

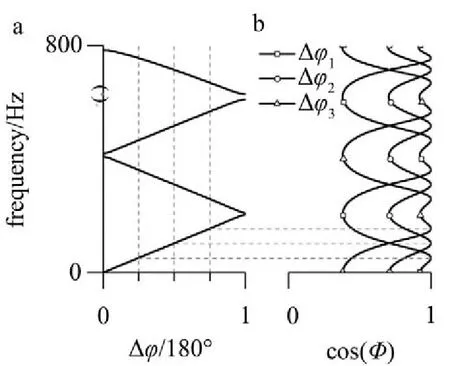
图4　频散曲线与功率因数之间的关系

对于有限长周期结构，其真实工作状态下的(Δφ,ω )并不一定恰好落在频散曲线上。因此，在图4(a)所示的Δφ-ω平面上，还有大片空白区域的能量传输特性有待进一步梳理。根据图4所示的仿真结果，既然频散曲线具有效率意义，若加以推广，再将前述功率因数响应表面上极大值、极小值相连，即可绘制出所谓“半高线”、“槽线”。根据脊线、半高线和槽线，可将Δφ-ω平面划分为一系列能量传输高效区和低效区。下面将用效率指标η代替cosϕ绘制上述各类曲线，其理由如下：

(1)效率指标η综合考虑了输入端驱动力和速度，能更全面地体现描述传输功率时所需建立的输入端场能，特别在λ≠1情况下更有实际意义；

(2)对于均匀媒质中的单列纵波，效率指标η=1与功率因数cosϕ=1存在等价关系（根据纵波特性3），因此指标η可以视为一种广义的功率因数。

图5(a)和图5(b)的左半部分分别给出λ=1和λ=0.5时，效率指标η响应表面的脊线、半高线、槽线在Δφ-ω平面上投影线；在右半图中，特给出Δφ=90°时的η随频率变化曲线。在左半图中，槽线的投影线恰为过fi(i=1…4)的水平坐标线，故略去；fi(i=1…4)分别对应前4阶自由-自由边界下的固有频率：f1、f2、f3、f4分别为210 Hz、421 Hz、629 Hz和800 Hz。在右半图中，特给出Δφ=90°时的η随频率变化曲线。

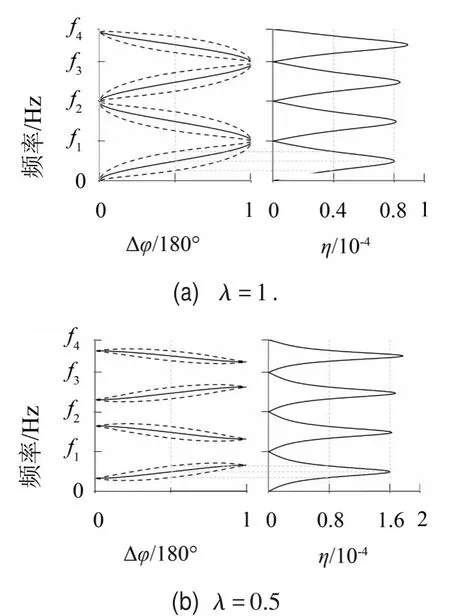
图5　效率指标η响应表面的脊线（——）、半高线（––––）、槽线的投影线

3　讨论

若输入/输出端振幅相同，在Δφ-ω平面上所绘制出的功率因数响应表面的脊线，就是周期结构行波解的频散曲线。这意味着可以用效率指标的等高线簇，将Δφ-ω平面划分为能量传输高效区和低效区。其中能量传输低效区意味着传输相同功率，需要在输入端维持较高的能量水平，换句话，如果输入端能量一定，该区域内的振动能量传递受到抑制。由此可见，效率观点的引入，有助于将周期结构带隙理论拓展到非行波解范畴，为描述有限周期结构的能量传输特性提供有力工具。

图5(a)左半图所示η函数的脊线，其形状与如图4(a)所示的频散曲线相近：均为一条从原点出发的螺旋线（在圆柱面上一条螺旋线沿径向投影可形成图5(a)左半图中的脊线），在脊线两侧分布有效率半高线。利用脊线与相邻半高线就可确定某一频率下，落在能量传输高效区时对应的Δφ范围。显然，Δφ范围越窄意味着对应频率的能量传输能力越差。例如，在图5(b)左半图中的灰色条形区域内，无论Δφ取任何值，都对应能量传输低效区。显然，上述频率范围划分方法与带隙频率确定方法是完全一致的。

对比图5(a)和图5(b)中的左半部分，不同振幅比λ下，脊线与半高线所围面积有所不同，这反映了效率指标η频域曲线陡峭程度不同，这一点也可以从右半图对比看出。对比图5(a)和图5(b)中右半部分所示的曲线峰值，可以发现λ=1时，η的局部极大值均小于λ=0.5的情况。注意到行波模式属于λ=1的情况，这说明对于有限周期结构，某些非行波解的能量传输效率反而要高于行波解，所以非行波模式对于有限周期结构的能量传输贡献不可忽视。

利用Δφ-ω平面上的η函数等高线族，可以对已有周期结构隔振设计方案进行评估，例如根据实际边界条件，可计算出，从而确定其是否落在所期望的能量传输区域内；然而，根据上述等高线族，如何在输出端确定合适的边界阻抗参数；或者根据已有边界阻抗，如何设计合适的周期结构，都是下一步需要研究的。

4　方法

本文所涉及的仿真均在ANSYS软件中实现。其中桁架的各杆单元类型为Link180。利用Harmonic模块，获得图3(b)中的各边界角点I～IV的几何约束反力FI、…、FIV。针对不同Δφ，逐个计算节点力F的频率响应，即可获得一张二维数据表

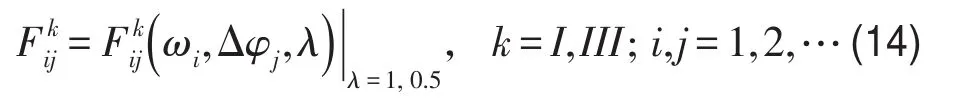
其中频率步长为1 Hz，相位差Δφ步长为1°，范围从1°～179°。利用输入端的节点力即可方便地计算出功率因数cosϕ以及效率指标η的响应表面，从而在平面上绘制出有关曲线。

图4(a)所示的频散曲线按如下方式绘制：根据二维数据表Fij(i为行指标，j为列指标)，针对每一列数据，查询符合行波解判定式的行指标i，从而确定一系列存在行波解的角频率ω*；遍历指标j，重复上述查找过程，即可在平面上绘制出频散曲线。图5中的脊线、半高线的绘制方法类似，不再赘述。

5　结语

(1)周期结构行波解对应的频散曲线可视为功率因数等于1的等高线。因此，频散曲线具有功率传输效率意义。

(2)对于有限长周期结构，可以引入效率指标函数η，用于刻画一般振动模式下（行波或非行波）的能量传输效率。利用η函数响应表面的脊线、槽线和半高线，可以将频率-波数平面划分为一系列能量

[33] Suda Y, Nakadai S, Nakano K. Hybrid suspension system withskyhook control andenergy regenerationdevelopment of self- powered active suspension[J]. Vehicle System Dynamics, 1998, 29(S1):619-634.

[34]曹民，刘为，喻凡.车辆主动悬架用电机作动器的研制[J].机械工程学报，2008，44(11)：224-228.

[35] Li P, Zuo L, Lu J, et al. Electromagnetic regenerative suspension system for ground vehicles[C]//Systems, Man and Cybernetics (SMC), 2014 IEEE International Conferenceon. IEEE, 2014:2513-2518.

[36]王庆年，刘松山，王伟华，等.滚珠丝杠式馈能型减振器的结构设计及参数匹配[J].吉林大学学报(工学版)，2012，42(5)：1100-1106.

[37]计民.汽车内燃机原理[M].上海：同济大学出版社，1997.

[38]朱智富.汽车废热利用的有效途径[J].黑龙江工程学院学报，2005，19(2)：51-53.

[39]陈家瑞.汽车构造[M].北京：机械工业出版社，2005.

[40] Hindi G, Zabeu C B, Langeani M. Turbocharged vs. turbocompounded ethanol engine:fuel- air equivalence ratio impact[R]. SAETechnical Paper, 2009.

[41]赵建云，朱冬生，周泽广，等.温差发电技术的研究进展及现状[J].电源技术，2010，34(3)：310-313.

[42]刘振全，肖尤明.轿车空调用单效溴化锂吸收式冷热水机组的探讨[J].甘肃工业大学学报，2001，27(1)：56-58.

[43]吴宝志，金永康.汽车空调[M].北京：宇航出版社，1991.

[44]刘士轩.利用汽车冷却废热驱动的喷射式制冷装置理论研究[D].长安大学，2007.

[45]（日）吉田佑作，祝玉文译，用排气涡轮发电机回收汽车发动机废热[J].新能源，1989，（7）：31-34.

[46]杨锡尧.余热氢气发生器-汽车环保、节能的关键技术[J].机械制造，2001，39(8)：31-31.

[47]张立军，李信中，刘炽棠.利用余热改善柴油机燃用重油后的性能[J].小型内燃机，1997，26(5)：1-4.

Study on the Band-gap of Periodic Structures in the Viewpoint of Power Efficiency

ZHOU Jun1, RAO Zhu-shi2, TA Na2
（1. Instituteof Vibration Shock & Noise, Shanghai Jiaotong University, Shanghai 200240, China; 2. StateKey Laboratory of Mechanical Systemand Vibration, Shanghai Jiaotong University, Shanghai 200240, China）

Abstract:Periodic structureistherepetitivein geometric configurationsor material properties, such astrussesand ribstiffened plates. In certain frequency bands, periodic structure can isolate the incident travelling waves. This property is widely applied in vibration isolator’s design. Generally, the analysis of periodic structure’s attenuation property is always based on infinite length assumption. It means that the periodic structure can extend infinitely in space. So, only travelling wave solutions have physical significance and the non- travelling wave solutions are neglected. However, the periodic structure in engineering is finite and the non-travelling wave solutions exist indeed. Therefore, the investigation of their power transfer propertiesisof significance. Thefiniteelement simulationsof theperiodic trussshow that thepower factor of the travelling wave solution is always equal to unity. It means that the dispersion curves are related to power transfer efficiency. Hence, the efficiency index function is introduced. According to the local maximum and minimum values of the index function’sresponsesurface, thefrequency-wavenumber spacecan bedivided into aseriesof high efficiency and low efficiency transfer regions. This method can be applied to both traveling and non-traveling wave solutions. The method extends the scope of band-gap analysis and gives an alternative approach for finite periodic structure’s power transfer analysis. Theresultsof thepresent work areof significancefor vibrationisolator’sdevelopment.

Key words:vibrationandwave; periodicstructure; power factor; efficiency; band-gap; truss

通讯作者：饶柱石，男，博士生导师。E-mail:zsrao@sjtu.edu.cn

基金项目：国家重点基础研究发展计划资助项目(2014CB046302)

作者简介：2015-0-17 周俊(1983- )，男，上海市人，博士生，主要研究方向为结构波动分析计算。

文章编号：1006-1355(2016)02-0001-05+45

中图分类号：O328；TB535

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.001